隨機利率下由Lévy過程驅動的期權定價

(山東科技大學 數學與系統科學學院，山東 青島 266590)

隨著現代資本市場的不斷發展，國內金融衍生產品市場迎來蓬勃發展的大時代。期權作為全球最為活躍的金融衍生產品之一，是金融產品創新的前沿，與現貨、期貨一同組成穩定的金融體系。期權受市場中利率波動的影響，各種利率衍生產品的交易成為期權定價研究領域的熱點問題之一。

對金融及其衍生產品給出一個合理的、使市場無套利的定價是當前研究的首要問題。然而在現實市場中利率不是一個常數，它是隨機變化的。許多學者在此基礎上進行了諸多研究：李淑錦[1]利用計價單位轉換的方法研究了隨機利率服從HJM模型條件下的期權定價問題，推導出了期權定價公式。劉堅等[2]在假設利率服從Hull-White模型、資產價格服從O-U過程條件下，利用保險精算方法給出了期權定價的公式。郭精軍等[3]利用對沖原理構造無風險資產，求得歐式期權在隨機利率模型下滿足的偏微分方程，經過變量替換獲得了歐式期權定價公式。1973年，Black和Scholes[4]假定股票價格過程服從幾何布朗運動，提出了經典的B-S期權定價公式。但這一條件要求過于苛刻，實際情況中股票的價格變化并不是完全服從布朗運動的。1988年，Lo等[5]在B-S公式基礎上提出股票價格存在“跳躍”的情況。此后越來越多的學者對標的資產價格存在跳躍的情況進行研究。黃伯強等[6-7]借助等價測度變換方法研究由Lévy過程驅動的期權定價問題，推導出了歐式期權定價公式。吳恒煜等[8]在此基礎上就無窮維純跳躍Lévy過程的期權定價問題進行了研究。鮑家勇等[9]利用傅里葉變換方法研究了資產價格服從隨機利率下由Lévy過程驅動的歐式期權定價。在假設利率是一個常數的條件下，文獻[10]研究了knight不確定環境下的lévy型金融市場中的期權定價問題，并得到了歐式期權動態模型定價區間。然而，在實際市場中，利率是隨時變化的，在隨機利率條件下給出確定性的期權定價公式，更能精確地預測金融市場中資產價格的變化情況。

本研究在利率隨機且服從Ho-Lee模型的條件下，借助Lévy-Laplace指數數學工具得到無套利條件下歐式看漲、看跌期權定價公式，并與標準的B-S期權定價公式進行比較，同時對股票價格服從Lévy純跳躍過程的期權定價問題進行進一步研究，利用泊松過程的性質得到Lévy-Laplace指數，建立無套利金融市場下帶跳的歐式期權定價模型，得到無套利約束條件下的歐式期權定價公式，拓展已有文獻的結論。

1 基本模型介紹

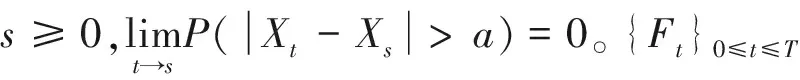
1.1 股票價格模型

假設Lévy過程{Xt}0≤t≤T的Laplace變換E[eλXt]有界，設0≤t≤T時刻股票的價格為S(t)，則標的股票價格過程為：

(1)

其中，μ、σ為常數，分別表示股票價格的期望收益率和波動率，且假設σ大于0，Bt是標準的一維布朗運動,S0是初始時刻股票價格。

引理1[11](Lévy-Laplace指數)Xt為Lévy過程，對任意t∈R+,λ∈(-∞,λu],λu≥0,存在一個函數Φ:(-∞,λu]→R使得E[eλXt]=etΦ(λ),稱Φ(λ)是Lévy過程Xt的Lévy-Laplace指數。

1.2 隨機利率模型

假設金融市場上的利率是隨機波動的，而金融產品的價格又受利率隨機波動的影響，基于此，對市場利率服從Ho-Lee模型的歐式期權價格進行討論。

Ho-Lee模型的利率隨機波動滿足

dr(t)=θ(t)dt+σrdB(t)。

其中，σr表示市場利率的波動率，θ(t)是關于時間t的函數。特別地，當θ(t)=0,r(0)=r時，上述模型將化為：

(2)

方程(2)所體現的利率瞬時運動只有擴散項σrdBt，而沒有漂移項，這說明了利率只是圍繞某一固定的常數值隨機波動，本身并沒有穩定移動的趨勢，初始值為r。這種利率模型在金融市場上有一定的市場解釋(文獻[11]曾利用該模型研究遠期的定價和風險研究)。在此模型基礎上，研究期權定價問題，該利率模型的解析形式為：

(3)

2 隨機利率環境下的期權定價

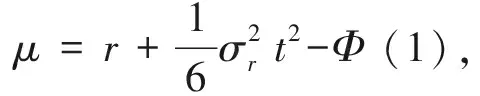
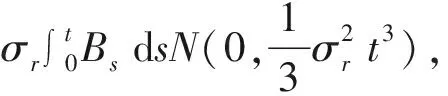
且由引理1可得

定理2在定理1條件下，利率隨機且運動方程滿足公式(2)時，歐式看漲、看跌期權的定價公式分別為：

(4)

(5)

其中，Ct、Pt分別表示到期日t時刻看漲期權以及看跌期權的價格，K表示敲定價格，σ、σr分別表示金融市場上股票價格和市場利率的波動率。

證明：在定理1條件下，歐式看漲期權

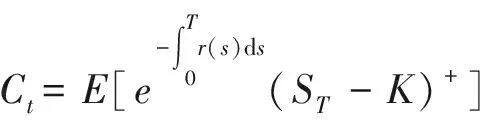
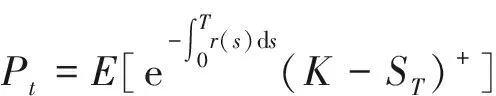
由上述定理可知，若不考慮隨機利率的影響，由標準布朗運動驅動下的標的股票價格過程的歐式看漲、看跌期權定價公式分別為

(6)

(7)

則利率隨機服從Ho-Lee模型下標的股票價格過程由Lévy驅動的歐式看漲、看跌期權的定價公式可分別記為：

(8)

(9)

由上可知，Ho-Lee模型下由Lévy過程驅動的股票價格的期權定價公式在形式上與傳統的B-S期權定價公式一致，可看作是對B-S公式的推廣。

3 Ho-Lee模型下Lévy純跳驅動下的期權定價

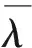
1)N(0)=0；

2)N(t)是獨立增量過程；

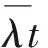
且V={Vi}i∈N+，Vi表示第i次跳躍的幅度，并且它是獨立同分布的躍度隨機變量，且滿足下列條件：

1)V0=1,Vi∈(-1,+∞);

2)對任意的v∈(-∞,1)，有E[(1+V)v]<∞。

Ft是由{Bt}0≤t≤T,{Nt}0≤t≤T和{Vi}i∈N+共同生成的σ-域流，三者彼此獨立。此時股票價格過程為：

(10)

由Possion過程的性質可得到：

定理3在無套利約束條件下，股票價格過程(10)的歐式看漲期權的定價公式為：

(11)

其中，

假設躍度Vi=h≠0(i=1,2,…)。

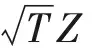
(12)

因此

從而:

(13)

則由ST>K,計算公式(13)括號中的表達式。即

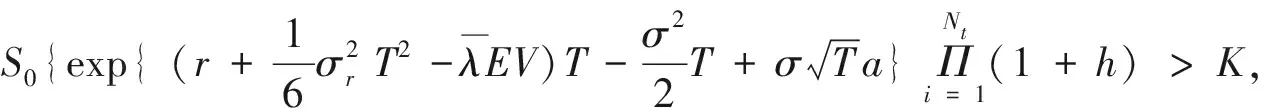
可得期權價格

(14)

把上述積分分成兩部分：

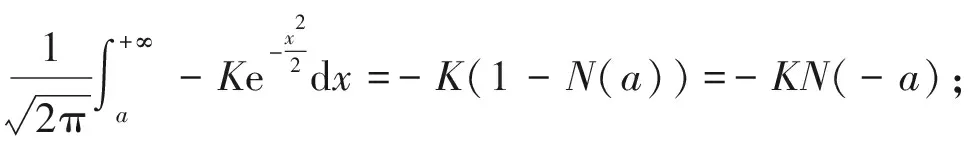
(15)

第一項

(16)

記

將式(15)、(16)代入式(14)可得看漲期權的定價公式

4 小結

在金融市場中，期權的價格不僅受標的價格變動的影響，而且與利率的波動密切相關。利率是決定所有金融衍生產品價格的一個重要因素，考慮了利率的隨機性對股票價格的影響，將利率服從Ho-Lee模型和標的資產服從Lévy驅動的過程結合在一起，建立了新的隨機微分方程，使得股票定價更加貼合實際。利用Lévy-Laplace指數研究了歐式期權定價問題，研究了在股票價格存在連續跳躍的情況下，借助Poisson過程和Lévy-Laplace指數數學工具得到了無套利金融市場下歐式看漲期權定價公式。本研究進一步豐富和拓展了文獻[4]中的期權定價理論，結論可進一步拓展到其他類型期權的定價研究中。