一類惡性腫瘤增長模型的穩定性分析
王國波
太原科技大學應用科學學院,山西 太原 030024
癌是醫學上對惡性腫瘤的一種通稱.癌細胞幾乎可以影響到身體的每個器官,其主要特點是可以使得正常細胞失去調節生命的能力.這種現象使它們能夠超越正常的界限,侵入周圍的組織和器官而導致患者死亡,醫學上稱之為癌癥擴散.
近幾年,數學模型成為數學家和生物學家研究癌癥復雜動力學行為的主要工具之一.癌癥數學模型建立的過程必須和臨床結果、實驗數據相吻合,同時也要考慮腫瘤細胞和免疫細胞之間的相互作用.這種復雜的模型過程數學家主要利用微分方程進行建立,通常是常微分方程和時滯微分方程對模型加以刻畫和描述.文獻[1~6]對癌癥以及關于癌癥所建立起來的數學模型做了大量有意義的工作.
De Pillis LG和Radunskaya A在文獻[7]中建立了惡性腫瘤模型:
(1)
其中,T(t)表示t時刻腫瘤細胞的密度;N(t)表示t時刻健康的宿主細胞的密度;I(t)表示t時刻單個腫瘤間隔區的效應免疫細胞密度;ri(i=1,2)分別表示腫瘤細胞和健康細胞在忽略其他細胞對其影響下的增長率;ki(i=1,2)分別表示腫瘤細胞和健康細胞的最大承載量;a13表示免疫細胞對腫瘤細胞的殺傷率;a21表示腫瘤細胞對健康細胞的滅活率;a31表示腫瘤細胞對免疫細胞的滅火率;d3表示免疫細胞的正常死亡率;a12,r3,k3分別表示正常數.文獻[7,8]利用局部緊不變集方法(LCIS)得到模型中腫瘤細胞消除的充分條件和腫瘤細胞不受約束下平衡點的全局穩定性.
本文在文獻[7]的基礎上研究在免疫細胞死亡這一極端條件下的腫瘤細胞和健康細胞的動力學行為,以便更好地分析腫瘤細胞擴散的復雜過程.文章主要對腫瘤細胞和健康細胞模型平衡點穩定性進行了定性分析,并給出模型在正平衡點處經歷Hopf分支的條件.
1 模型在x3=0限制條件下的穩定性分析
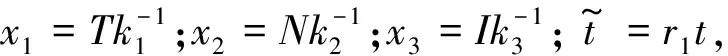
(2)
為了更好地理解系統(2)在最大不變集上解軌跡的情況,我們假設x3=0.于是方程(2)變為
(3)
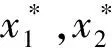
(A1):r2>a21,1>a12.
(A2):r2 下面我們接著分析方程(3)在四個平衡點處穩定性以及Hopf分支存在性.以此,我們假設 則方程(3)的線性化方程為 其中 定理1若(A1)成立時, 在平衡點Si(i=1,2,3)處不穩定. 證明 當S=S1時,方程(3)在S1處對應線性化方程的特征方程為 (1-λ)(r2-λ)=0 于是得λ1=1>0,λ2=r2>0所以方程(3)在S1處不穩定.同理方法我們可以同樣處理S2,S3. 在條件(A1)成立時,對于S=S2,可得到其對應特征方程的根為λ1=1>0,λ2=r2-a21>0,所以方程(3)在S2處不穩定. 對于S=S3,可得到其對應特征方程的根為λ1=a12-1>0,λ2=-r2<0所以方程(3)在S3處不穩定.證畢. 定理2方程(3)滿足如下: (i)當A1(r2)>0,A2(r2)>0時,方程(3)在S4處漸近穩定; (ii)當(A1),(A3)~(A5)成立時,方程(3)在S4處產生Hopf分支. 證明 當S=S4,可得到其對應特征方程為 λ2+A1(r2)λ+A2(r2)=0 (4) 其中 于是得 利用Routh-Hurwotz[9]準則法可得出,當A1(r2)>0,A2(r2)>0時,方程(4)的所有根都具有嚴格負實部,則有方程(3)在S4處漸近穩定. 同時滿足 (a)方程(3)在t-x1坐標下的波圖(b)方程(3)在t-x2坐標下的波圖 圖1 方程(3)在特定參數下數值解 (c) 方程(3)在x-y坐標下的相圖(d)(c)在(1,0)處局部放大圖 圖2 方程(3) 的相圖 本文主要利用常微分方程的定性理論分析了惡性腫瘤增長模型平衡點處的穩定性并給出系統產生Hopf分支的條件,同時數值模擬得出方程的解收斂到死亡平衡點.然而,此模型在參數變化情況下還有許多更有意義的分支現象,它們將可能在醫學上對癌癥治療方案產生積極的意義,這些問題有待于進一步的分析和研究.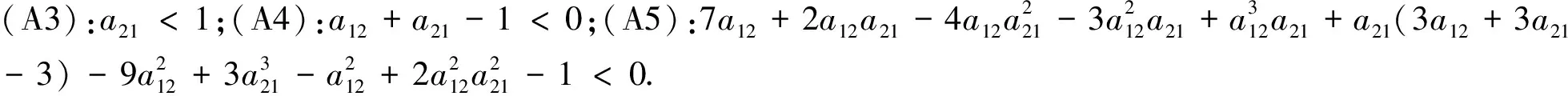
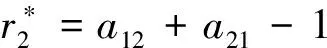



2 數值仿真
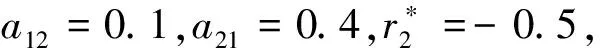

Fig.1 Simulated solution of equation (3)
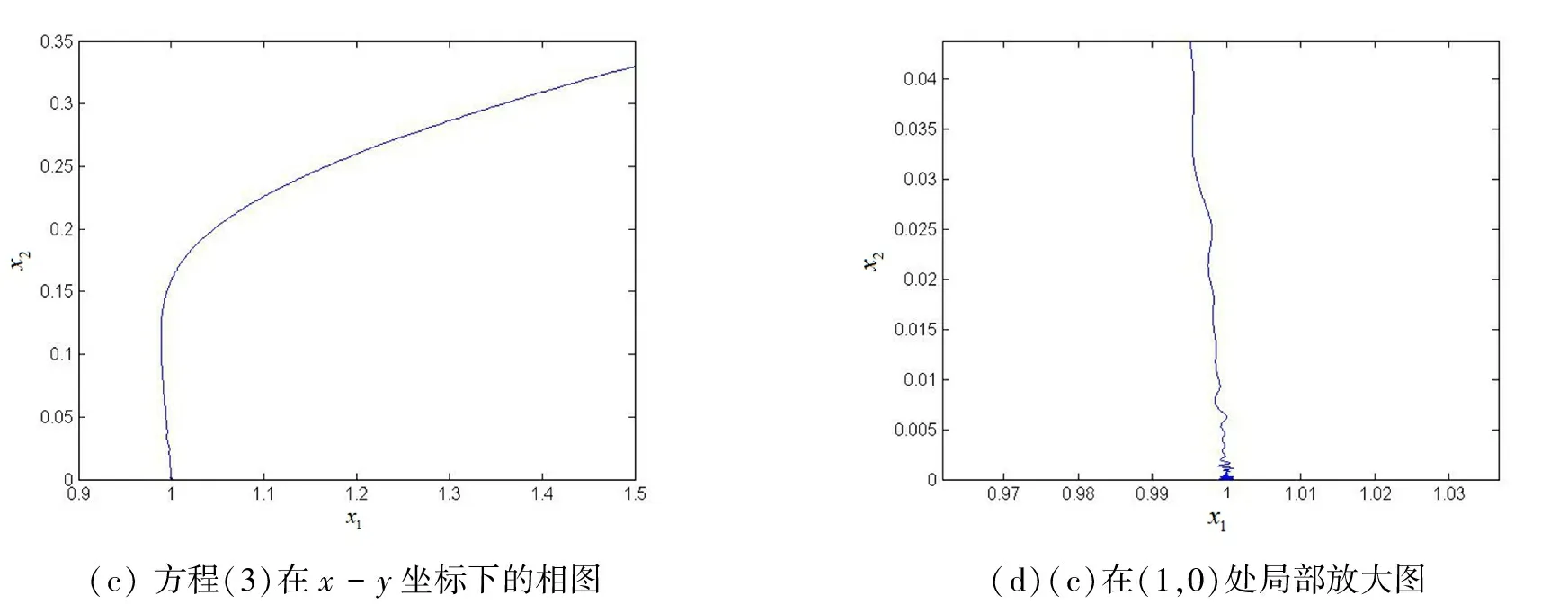
Fig.2 Phase plots for equation (3)3 結語

