基于并行蟻群算法的長基線定位方法?

張海如 汪 俊 王海斌

(中國科學院聲學研究所 聲場聲信息國家重點實驗室 北京 100190)

0 引言

目前，世界各國正積極實施“數字海洋”戰略。水下導航定位技術在“數字海洋”戰略中扮演著非常重要的角色。如何實現水下高精度導航定位已成為海洋開發與利用中最迫切的問題之一[1?3]。長基線(Long baseline,LBL)定位系統具有定位精度高、可靠性好、可進行大面積和深水海域的定位等優點，獲得了國內外該領域多個研究機構的研究興趣。文獻[4]針對測量誤差影響全向聲吶浮標目標定位精度的問題，提出了采用總體最小二乘法對水下目標進行定位，仿真結果表明該方法優于求解定位方程組最小二乘解方法；文獻[5]將同步模式下的水下目標定位問題簡化為求解矩陣方程的問題，即采用球面交會的方法對目標進行定位，在此基礎上，分析了目標測量深度誤差、基元測量時間誤差、基元位置測量誤差、聲速誤差等相關參數的測量誤差對定位精度的影響；文獻[6]提出了一種改進的水聲網絡定位算法，該算法在進行定位運算前先對原始數據進行降噪處理，以提升其抗噪能力，同時降低了計算結果的冗余性。上述研究中都是將水聲目標導航定位問題抽象為求解矩陣方程最小二乘解的問題。然而，由于水下環境的復雜性，水聲目標定位是帶約束條件的非線性優化問題，約束條件包括：聲速誤差、航行噪聲、應答器偏移和載體搖擺等。將帶約束條件的非線性優化問題退化為求解矩陣方程最小二乘解的問題，雖然降低了問題求解的復雜度，但這是以降低水下目標導航定位精度為代價的。隨著海洋相關的各種應用領域中對水下目標導航定位的精度要求越來越高，高精度時延估計和帶約束條件的非線性優化技術成為水聲導航定位領域的研究熱點。

時延估計精度是影響定位誤差的關鍵指標之一，如何提高時延估計精度，已經成為該領域專家們的熱點研究問題。文獻[7]采用倒譜方法估計水聲信號的時延，實驗結果表明該方法適用于高信噪比條件，其時延估計精度優于廣義互相關方法。文獻[8]采用Chan算法獲得的到達時間差(Time difference of arrival,TDOA)定位結果作為Taylor 算法的初始值，提高了基于Taylor 算法的TDOA 定位精度，并采用仿真實驗驗證了該方法的有效性。文獻[9]采用相關峰分辨和穩定相關峰跟蹤相結合的方法，以消除近程TDOA 被動定位中互相關峰模糊問題，并通過海上實驗驗證了該方法的有效性。文獻[10]采用對數域同態濾波技術來降低多途對水聲信號時延估計的影響，該方法先將接收信號進行對數變換，然后將其與本地信號進行譜減處理，再對處理后的信號進行濾波消除噪聲分量和殘留信號分量，最后將處理后的信號變換到時域，以獲得時延值，實驗結果表明該方法時延估計精度優于復倒譜估計法。但是由于該方法對信號進行處理過程中使用了譜減法，當接收信號與本地信號存在較大頻移時，該方法無效。目前，絕大部分研究成果都是從提高時延估計精度的角度，提高LBL系統定位精度。但是，受水聲信道的多途特性影響，目標信號的到達時刻具有測不準性，限制了LBL系統定位精度的進一步提高。

為了進一步提高LBL 導航定位系統的定位精度，本文研究了利用同步信標對目標進行導航定位的問題，將水聲目標導航定位問題抽象為帶約束條件的非線性優化問題，論證了最優化表達式參數求解過程與降低誤差源干擾的過程具有同一性，并采用并行蟻群算法(The parallel ant colony algorithm,PACA)求其最優解，最后通過海試數據驗證該方法的有效性。

1 基于最優化模型的LBL定位方法

LBL 定位系統由多個同步信標構成，信標位于不同站點處，水下目標通過接收多個信標發射的導航信號，實現對自身的定位。令目標在A點處的時刻收到站點i處在時刻發送的導航信號，A點和站點i的坐標分別為(x,y)和(xi,yi)，A點與站點i之間的距離為ri，該時間段內導航信號從站點i處傳播到A點的平均聲速為Ci，Ci的值根據發射和接收站點的水文環境參數信息通過KrakenC 計算得到[11]，目標收到導航信號的站點數為N，A點為待求解位置，滿足方程組：

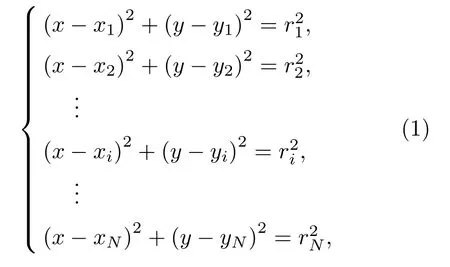
上述模型為二維平面導航定位模型，當導航定位距離與海深的比值大于100 時，按照二維平面和三維球面兩種導航定位模型計算得到的兩點間距離之差小于2 m，由此導致的定位誤差與測時、聲速估計等其他原因導致的定位誤差相比要小1～2 個數量級，因此可以忽略不計。上述模型適用于淺海遠距離導航定位求解。

在矩陣方程組(1)中，由于GPS 接收模塊存在定位誤差，會導致站點i的坐標(xi,yi)存在誤差；由于信道起伏、多途以及噪聲干擾等原因，會導致導航信號最佳到達時刻存在估計誤差；由于收發系統的同步誤差，會導致導航信號發送時刻和到達時刻存在測量誤差；由于水聲信道的非均勻性，采用發射和接收站點的水文環境參數信息，估計收發站點之間的平均聲速Ci存在較大誤差，并且聲速估計誤差引起的測距誤差會隨著距離的增大而增大。由于上述各種誤差源的存在，直接采用矩陣方程組(1)的最小二乘解作為目標位置信息存在較大的定位誤差。

為了進一步提高導航定位系統的定位精度，本節將矩陣方程組(1)轉化為帶約束條件的非線性優化問題：

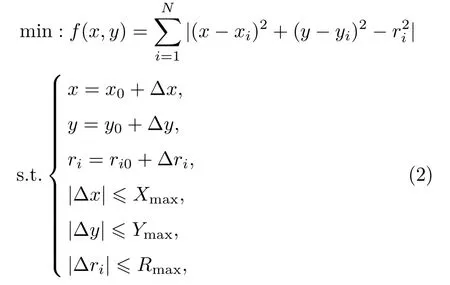
其中，?x、?y和?ri是目標函數中參數x、y和ri的調整量；Xmax、Ymax和Rmax是目標函數中參數x、y和ri的最大調整量。求解式(2)過程中，三個參數、和Ci的各自誤差都作用在參數ri上，構成綜合誤差?ri，通過對參數ri的調整可以同時降低收發系統同步誤差、測時誤差以及聲速估計誤差對定位精度的影響，而且需要調整的參數個數得到有效的降低，有利于提高目標函數求解效率。求解式(2)所示的最優化問題，即可得到目標位置的最優估計值。

2 PACA求解目標位置信息

由于求解目標位置信息的目標函數表達式(2)是比較復雜的多極值問題，不能用解析法對其進行求解，本文采用迭代搜索的方法求其最優解或者近似最優解，這類逼近真實解的近似解在工程項目中仍具有現實意義[12]。蟻群算法[13]是一種啟發式算法，該算法本身具有隨機性，當前，其收斂性還沒有嚴格的數學證明，但是大量實踐表明其在求解最優化問題中性能優異，已成為一種高效的最優化問題求解工具。為了求解表達式(2)中的目標位置信息的最優解或者近似最優解，設計了并行蟻群算法(PACA)，避免單次求解獲得較差的局部最優解；同時，PACA在蟻群算法的基礎上進行改進，采用變步長搜索，以兼顧蟻群算法的求解效率和求解精度，即先采用較大步長搜索粗略解，隨著迭代次數的增加逐步縮小步長，以搜索精細解。PACA 系統框圖如圖1所示，即：同時且獨立啟動Q個子系統對表達式(2)進行求解，將各個子系統求解結果代入表達式(2)，從中選取最優解，該最優解作為目標位置的最優估計值。

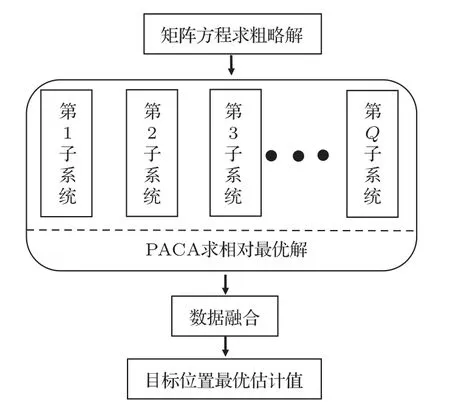
圖1 PACA 用于LBL 定位的系統框圖Fig.1 PACA system block diagram for LBL positioning

PACA 的各個子系統求解表達式(2)中的目標位置信息的最優解或者近似最優解，其實現步驟如下：

步驟1 算法初始化。求解方程組(1)獲得參數x、y的初值；最大迭代次數為Nmax；初始迭代次數為Num = 0；每一代蟻群的個體數為P；目標函數求解精度閾值為θ。模型求解的收斂速度與適應度函數所對應的組合優化參數的個數有關，組合優化參數個數越少，收斂速度越快，模型求解所需迭代次數越少。本文適應度函數中組合優化參數個數為3，組合優化參數規模較小，通常迭代求解30 次后，適應度函數能收斂到穩定殘差。

步驟2 計算下一代搜索路徑。下一代搜索路徑更新公式為

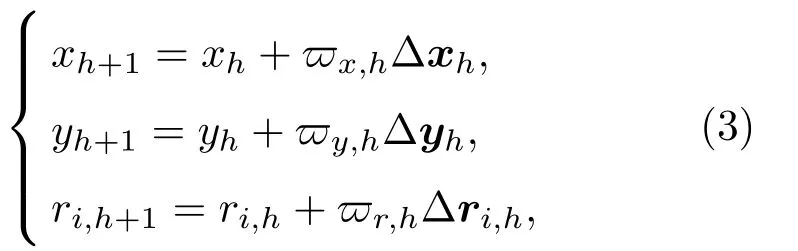
其中，wh為移動權重，h為迭代次數標記，?xh、?yh和?ri,h為移動方向向量，xh、yh和ri,h為當前一代參數值，xh+1、yh+1和ri,h+1為下一代參數值。為了加快收斂速度，同時保證計算精度，采用變步長搜索wx,h= (1?Num/Nmax)Xmax、wy,h=

移動方向矩陣為

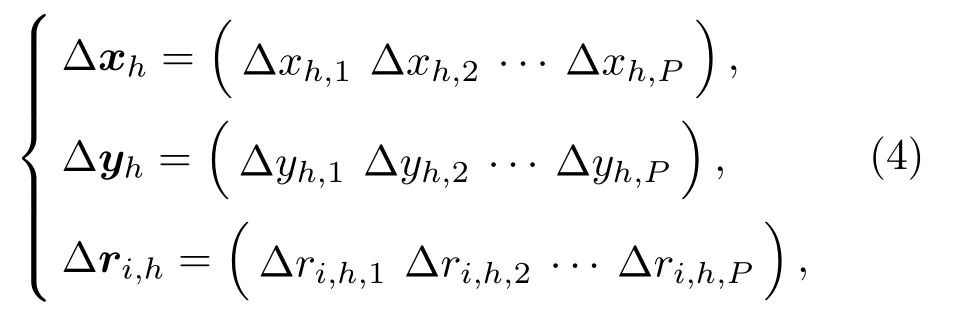
其中，?xh、?yh和?ri,h中各個元素均為±1 之間的隨機數。

步驟3 計算適應度函數，更新最優解。將步驟2 中當前一代中每一個體代入表達式(2)，計算當前一代最優解。

步驟4 判斷迭代是否停止。如果迭代次數達到Nmax，或者當前最優適應度函數值小于θ，則停止迭代，目標定位結果為當前最優解；否則，返回執行步驟2。

上述算法時間復雜度分析：PACA 的單個子系統求解表達式(2)中的目標位置信息的最優解或者近似最優解的時間復雜度為O(Nmax·P ·n2)[14]，其中n為適應度函數所對應的組合優化參數的個數，本應用中n= 3。在本應用中，由于組合優化參數規模較小，其計算效率較高。

3 海試數據驗證及結果分析

為了驗證PACA用于LBL定位的性能，本文將該方法定位結果與求解方程組(1)獲得的定位結果進行對比分析。實驗海區距離岸邊約60 海里，水深30～50 m，泥沙底質。整個實驗為一個航次，采用雙船作業，其中科學三號為接收船，金星二號為發射船。在本次實驗中，由于只有一艘發射船發射導航信號，發射船需要機動才能在不同位置發射導航信號，因此接收船需要等待一定的時間才能收到發射船在多個不同位置發射的導航信號。在此期間，接收船采用船首拋錨方法，并通過GPS接收模塊來獲知本船的位置漂移。在本次實驗中，接收船和發射船的位置分布如圖2所示，在圖2中接收船在坐標原點(站點M)處拋錨，站點M用“O”表示；發射船分別位于站點1、站點2、站點3 和站點4，其中，在站點1、站點2 和站點3 采用定點吊放聲源發射導航信號，發射船在站點4 從L1 運動到L2 采用拖曳聲源連續發射導航信號，以便于驗證不同距離定位精度，站點4包含436個測點。在本次實驗中，由于海深只有30～50 m，而導航距離在30 km 以上，因此將測量得到的聲傳播距離直接作為其在平面坐標系上的投影距離，由此導致的定位誤差與測時、聲速估計等其他原因導致的定位誤差相比要小兩個數量級以上，因此可以忽略不計。

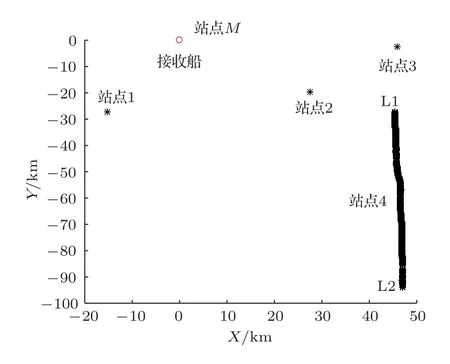
圖2 接收船和發射船的位置分布Fig.2 Position distribution of receiving and launching vessels

本實驗選取圖2所示的站點1、站點2、站點3和站點4 作為發射位置，對接收船進行定位，由于站點4 包含436 個測點，實驗獲得436 個定位結果。PACA 求解最優化表達式(2)的相關參數值初始化如下：參數x、y和ri的最大調整量Xmax= 50、Ymax= 50 和Rmax= 40；求解表達式(2)的子系統數Q=10；各子系統的最大迭代次數為Nmax=50，每一代蟻群的子個體數為P= 40，θ= 500。對站點4 的第1 個發射點，PACA 的第一個子系統求解表達式(2)對應的目標函數收斂曲線如圖3所示。由聲學方法得到的接收船位置與由接收船GPS 接收模塊得到的真實位置之間的誤差如圖4所示，其中，虛線為求解方程組(1)獲得的定位結果對應的定位誤差曲線，實線為PACA 方法求解最優化表達式(2)的定位結果對應的定位誤差曲線。

圖3表明PACA 方法求解表達式(2)所示的最優化問題具有較好的收斂性。在圖4所示的定位誤差曲線對比圖中，采用計算矩陣方程的最小二乘解的定位方法，其定位誤差的最大值為147.13 m、最小值為47.60 m、平均值為81.37 m；采用PACA 求解最優化表達式(2)的定位方法，其定位誤差的最大值為104.35 m、最小值為7.09 m、平均值為50.46 m。上述實驗結果表明，采用PACA 求解最優化表達式(2)的定位方法，通過在目標位置的最小二乘解和收發點的距離估計值附近啟發式搜索，能降低收發系統同步誤差、測時誤差、聲速估計誤差等對適應度函數的干擾，能對適應度函數起到優化作用，進而提高目標定位精度；蟻群算法求解最優化表達式(2)可能獲得局部最優解，采用PACA 方法獲得的目標位置估計值更接近適應度函數的全局最優解。由于單個子系統求解表達式(2)的收斂速度較快，迭代20 次左右即可獲得平穩殘差。當并行子系統數Q較小時，可以采用Q次單個子系統串行求解的方法來等效并行求解；當并行子系統數Q較大時，為了提高目標定位的實時性，可以采用GPU 系統進行并行運算。

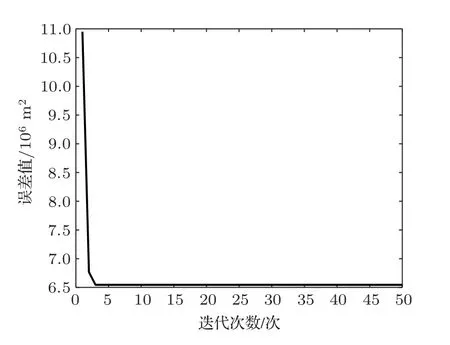
圖3 收斂曲線Fig.3 Convergence curve

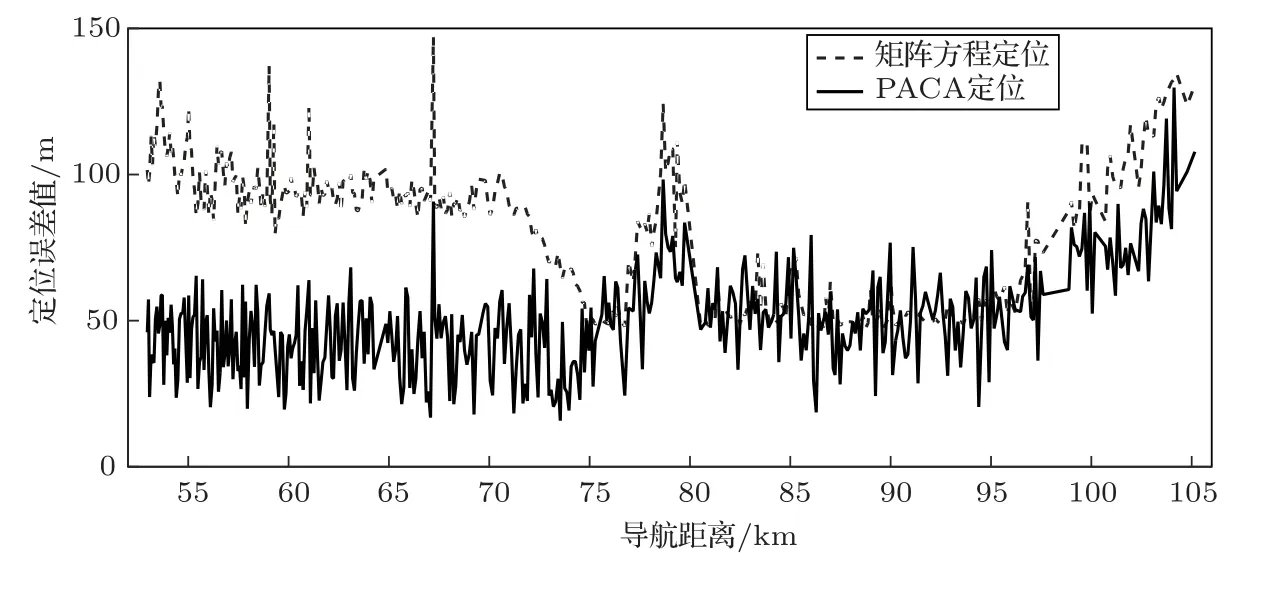
圖4 定位結果誤差曲線的對比Fig.4 Comparison of the error curve of the location result

4 結論

本文將LBL 水聲導航定位問題抽象為帶約束條件的非線性優化問題，并采用PACA求其最優解。采用定位方程組的最小二乘解作為系統的初始值，降低了最優解的搜索區間，能提高系統求解效率；與采用單獨的蟻群算法求解相比，采用PACA 進行求解，能降低算法本身可能陷入局部最優解的影響，有利于提高解的精度和穩定性；采用PACA 進行目標函數求解的過程中，令其搜索步長隨著迭代次數的增加逐漸減小，既能提高算法迭代收斂速度，又能保證解的精確度。海試數據處理結果表明，與傳統的求解定位方程組的最小二乘解相比，本文方法平均定位誤差降低了30 m，能有效降低各個誤差源對水聲目標導航定位精度的影響。