“特殊平行四邊形”的兩種開放題型解法剖析
趙萌
【摘要】本文主要是從兩種題型著手來研究“特殊平行四邊形”的.一種是給出結論探索條件的題型,另一種是已知條件來探索結論的題型.這兩種題型具有開放性,主要考查了平行四邊形、菱形、矩形、正方形等之間的判定關系,是中考常考題型,學生必須熟練掌握.
【關鍵詞】特殊平行四邊形;判定;開放題型
一、中考分析
平行四邊形及特殊的平行四邊形是中考的重點之一,在中考中出題的頻率較高,命題形式靈活多樣,難度以中檔為主,熱點較多.而有關特殊的平行四邊形的開放探索題也成為近幾年的熱點、難點問題.
二、題型探討
(一)已知結論,探索條件
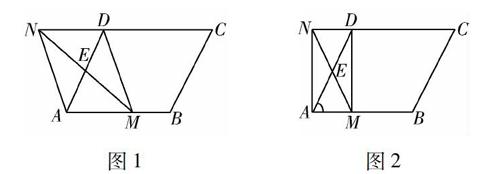
例1 (河南)如圖1所示,在菱形ABCD中,AB=2,∠DAB=60°,E是AD邊的中點,點M是AB邊上一動點(不與點A重合),延長ME交射線CD于點N,連接MN,AN.
(1)求證:四邊形AMDN是平行四邊形;(2)填空:① 當M的值為時,四邊形AMDN是矩形;② 當AM的值為時,四邊形AMDN是菱形.
證 (1)∵四邊形ABCD是菱形,
∴∠NDE=∠MAE.
又∵E是AD的中點,∴DE=AE,
∴△NDE≌△MAE,∴ND=MA,
∴四邊形AMDN是平行四邊形.
(2)①解析:如圖2所示,若四邊形AMDN是矩形,則在Rt△AMD中,∠DAM=60°,∴AD=2AM.
又∵四邊形ABCD是菱形,∴AB=AD=2,
∴AM=1,∴當AM的值為1時,四邊形AMDN是矩形.
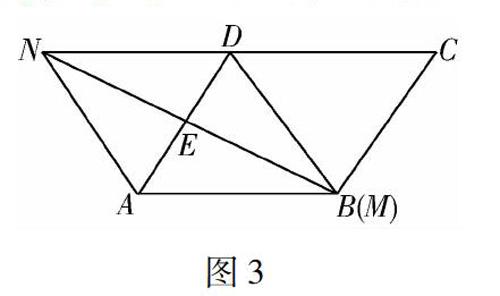
②解析:如圖3所示,若四邊形AMDN是菱形,
則AM=DB.
又∵AB=AD=2,
∴AM=AB=2,
∴當AM=2時,四邊形AMDN是菱形.
解法剖析 本題是給出問題的結論,分析探索使結論成立具備的條件,而滿足結論的條件往往不是唯一的,這樣的問題是條件開放性問題,解這類題的時候,要善于從問題的結論出發,假設結論成立,以結論為條件,逆向推導,多途尋求解法.在本例中的第二問,先畫出結論要求的矩形,再將矩形看成條件,根據矩形的角為直角和已知條件,構造直角三角形,解出AM的長.同理,當AMDN為菱形時,將結論菱形轉換成條件,逆向推出AM的長.
(二)已知條件,探索結論
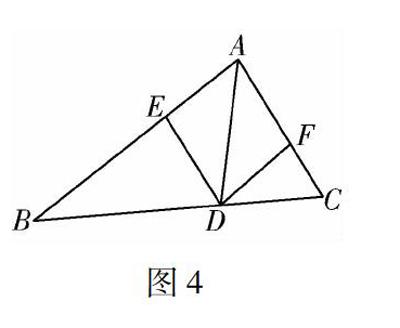
例2 (安順中考)如圖4所示,已知點D在△ABC的邊BC上,DE∥AC交AB于點E,DF∥AB交AC于F.
(1)求證:AE=DF.
(2)若AD平分∠BAC,試判斷四邊形AEDF的形狀,并說明理由.
解 (1)∵AE∥DF,DE∥AF,
∴四邊形AEDF是平行四邊形,∴AE=DF.
(2)若AD平分∠BAC,則四邊形AEDF是菱形.
理由:∵四邊形AEDF平行四邊形,∴∠EAD=∠ADF.
又∵AD平分∠BAC,∴∠EAD=∠DAF,
∴∠DAF=∠ADF,∴AF=DF,
∴平行四邊形AEDF是菱形.
解法剖析 給定問題的條件,根據條件探索相應的結論,并且符號條件的結論往往呈現多樣性或者相應的結論的“存在性”需要解題過程中學生進行推斷,甚至要求條件在變化中的結論,這些問題都是開放性問題,解這類問題要充分利用條件進行大膽合理的猜想,發現規律,得出結論.
變式 在例2的第(2)問中,若將“AD平分∠BAC”改為“∠BAC=90°”,則四邊形AEDF形狀如何呢?
解 矩形.理由:若∠BAC=90°,由(1)知四邊形AEDF是平行四邊形.
則四邊形AEDF是矩形.
解法剖析 在變式中,當要求在變化時,結論也在變化,由菱形變為了矩形.
因此,上述的兩種開放題型都必須熟練掌握四邊形判定之間的關系.
【參考文獻】
[1]李敏.《正方形的性質與判定》教學案例[N].發展導報,2018-09-28(21版).
[2]穆秋蓮.《平行四邊形、矩形、菱形、正方形》由一般到特殊圖形類比教學案例分析[N].發展導報,2018-07-31(19版).
[3]錢根林,徐志良.“平行四邊形、矩形、菱形、正方形”的復習(第一教時)[J].蘇州教育學院學報,1993(2):62-63.

