基于簡化Zig-zag模型的鋼聚氨酯夾層板屈曲分析

田阿利，張海燕，魏 震，趙元帥，傅梓軒

(江蘇科技大學 船舶與海洋工程學院，江蘇 鎮江 212003)

0 引 言

鋼/聚氨酯夾層板（Steel Polyurethane Steel Sandwich Plate）簡稱SPS夾層板，是由鋼質面板和聚氨酯彈性體夾芯材料組成，由于其輕質、高比強度等性能而成為現代科學的研究重點。目前，鋼/聚氨酯鋼夾層板已經應用于船舶修復上。2009年7月韓國大宇造船海洋工程公司與英國IE公司共同投資成立了“SPS海工技術公司”，雙方共同對SPS技術展開研究，并將該技術應用于船用鋼板的加工。當SPS夾層板應用于艙口蓋時，由于受風浪流的影響，使得航行中的船體發生中拱或中垂現象，此時，夾層板受面內載荷作用的影響，可能會發生屈曲失效導致結構發生破壞。因此對夾層板的屈曲性能分析日益重要且迫在眉睫。

對層合板和夾層板的屈曲分析可追溯到19世紀70年代，Srinivas和Rao[1]，Noor[2]建立了層合板和夾層板屈曲分析的彈性解。Reddy和Phan[3]提出采用高階剪切變形理論來研究層合板的振動和穩定性問題。Reddy和Putcha[4]基于改進的高階理論，利用混合單元對層合板的穩定性和固有振動進行研究。Fares和Zenkour[5]基于多種板理論研究了非均質復合材料交叉層合板的屈曲和自由振動問題。Kant和Swaminathan[6]提出一種改進的高階理論求出復合材料層合板和夾層板穩定性分析的解析解。Dafedar[7]使用分層理論研究了夾層板的穩定性，并獲得夾層板總體屈曲載荷和皺屈載荷，該理論考慮了夾層板中每一層的位移和應力，涉及到大量變量。Kheirikhah[8]使用改進的高階理論研究了軟夾芯復合材料夾層板的雙軸屈曲問題。Grover[9]等基于非多項式剪切變形理論研究了復合材料層合板和夾層板的靜態，振動和屈曲響應問題。Fazzolari和Carrera[10]使用卡雷拉統一公式（CUF）并結合里茨法（Ritz）和伽遼金法（Galerkin）研究了基于改進的變分運動板理論的各向異性復合材料層合板和夾層板的熱機械屈曲問題，給出了不同熱載荷和機械載荷下的屈曲相互作用曲線和穩定性包絡線。Khandelwal[11]采用9節點二次單元來研究復合材料層合板和夾層板的自由振動和屈曲響應問題。Ranjbaran等[12]基于LW理論研究了夾層板的穩定性問題，并采用瑞利-里茲法近似確定位移場。Birman和Kardomateas[13]對夾層板的理論分析方法進行了綜述。

由于理論方法受限于研究對象的幾何形狀，載荷和邊界條件，Di Sciuva[14]在1986年提出Zig-zag理論（ZZT）。該理論不僅能較真實地描述面內位移發生在厚度上的變化，而且也能較為準確地預測層合板和夾層板的面內位移和應力。作者采用該方法研究了復合材料層合板的靜態、振動和屈曲響應問題。白瑞祥等[15]利用Zig-zag理論對復合材料夾層板的自由振動問題進行了研究。Pandit等[16]基于改進的高階Zig-zag理論研究了夾層板的屈曲，考慮了芯材壓縮變形的影響。Sahoo[17]建立了反三角Zig-zag理論，該理論不僅滿足層間界面的連續性，又滿足板上下表面自由牽引的邊界條件。作者通過數值算例，預測了不同模量比、縱橫比、跨厚比、載荷和邊界條件下復合材料層合板和夾層板的屈曲響應。

基于以上討論可得出：單層板理論由于沒有考慮夾層板的層間影響而過渡預測屈曲臨界載荷；Layerwise理論由于需要較多的應變場導致計算量龐大，效率低下。

鋼聚氨酯夾層板的面板較薄，芯材較厚，因此橫向剪切變形不可忽略。文獻[18]對復合材料夾層的面板與芯材均采用了高階變形理論且取得了較為準確的結果，但因未知量過多，使得計算量太大。本文考慮鋼聚氨酯夾層板的結構特征，基于文獻[18]，提出一種簡化的高階Zig-zag理論，即面板采用1階剪切變形理論，芯材采用Reddy[19]的高階變形理論，來研究夾層板的穩定性。重點研究SPS夾層板作為艙口蓋受軸向壓縮載荷下的屈曲問題，分析幾何參數對結構穩定性的影響，為SPS夾層板在船體結構中的設計與推廣提供參考。

1 簡化的高階Zig-zag理論求解模型

在模型中，ht為上面板厚度，hb為下面板厚度，hc為芯層厚度。夾層板的典型坐標系及模型圖如圖1所示。

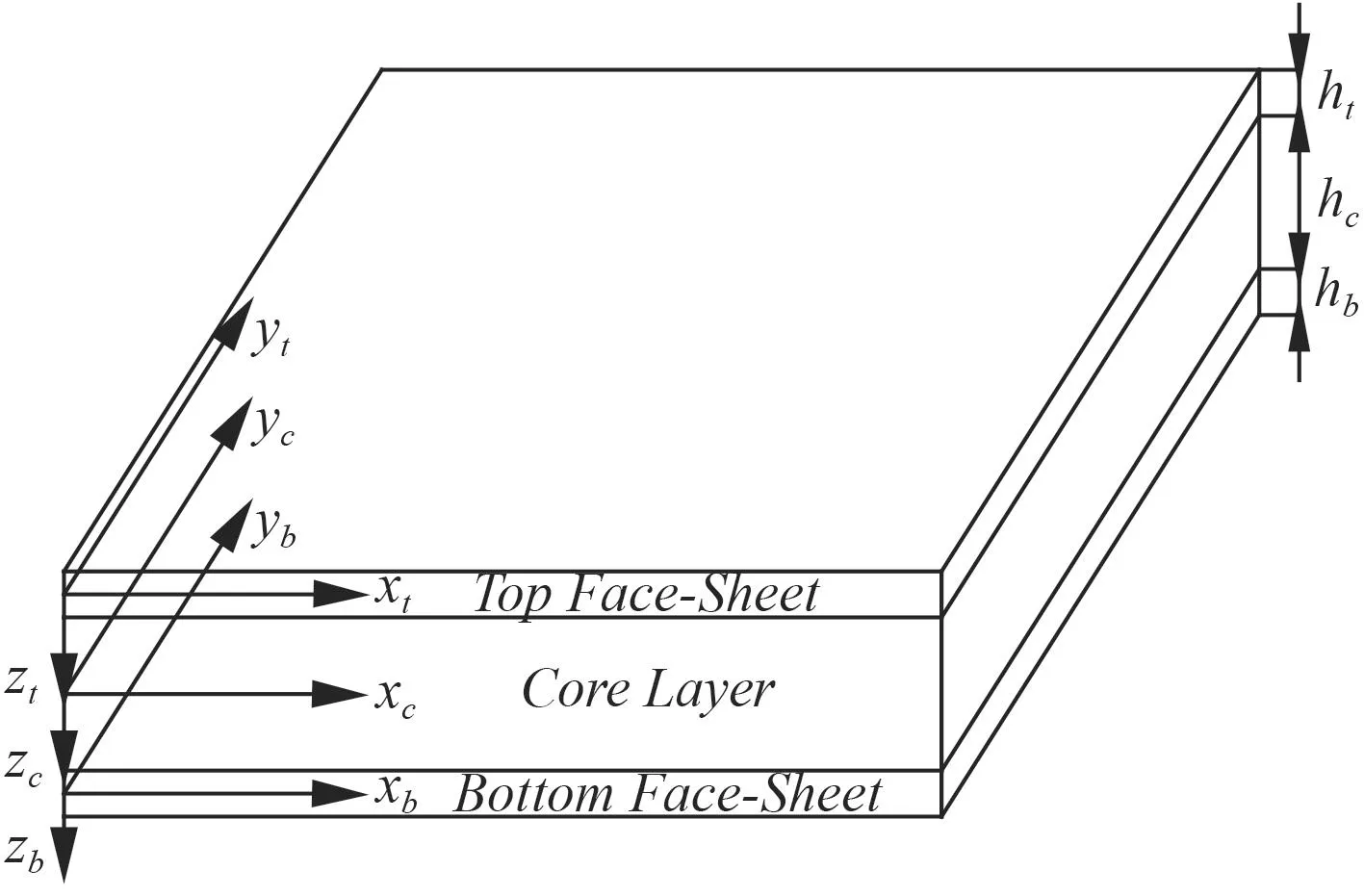
圖1 夾層板的典型坐標及模型圖Fig.1 Typical coordinate and model

1.1 動力學關系

夾層板面板的位移場函數為：

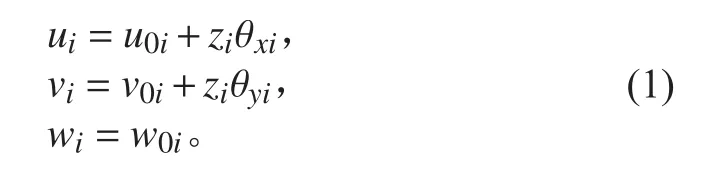
夾層板芯材位移場函數為：

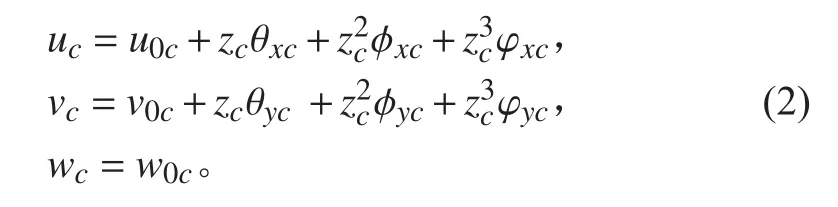
1.2 連續條件

1.2.1 位移連續條件

夾層板上面板與芯材交界處的位移關系：

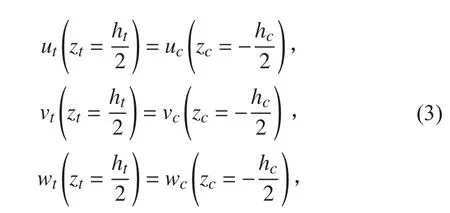
夾層板下面板與芯材交界處的位移關系：

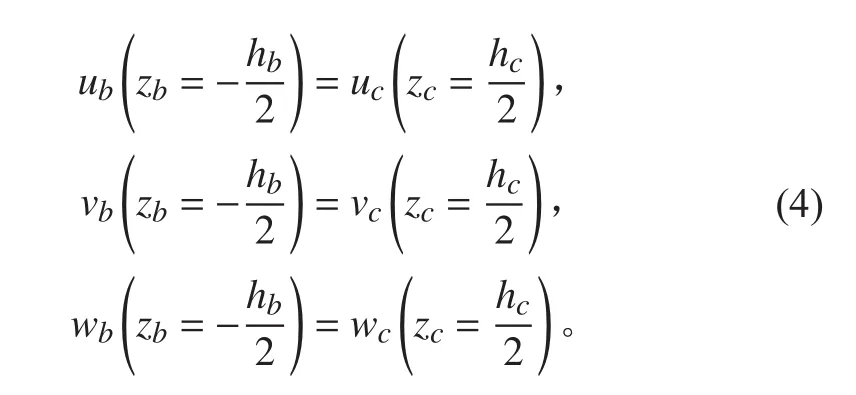
1.2.2 層間剪應力連續

上面板與芯材交界處的剪應力關系：

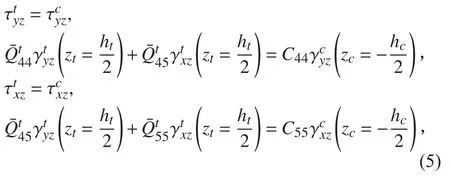
下面板與芯材交界處的剪應力關系：

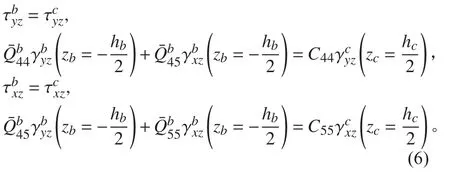
1.3 控制方程

根據哈密爾頓原理（Hamilton Principle）推導出夾層板面板和芯材的控制方程。

Hamilton原理的表達式如下：

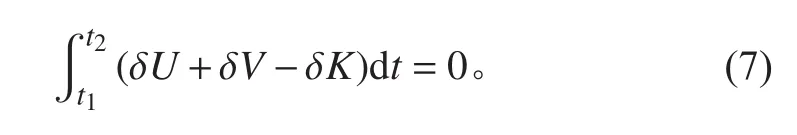
積分并整理得控制方程：

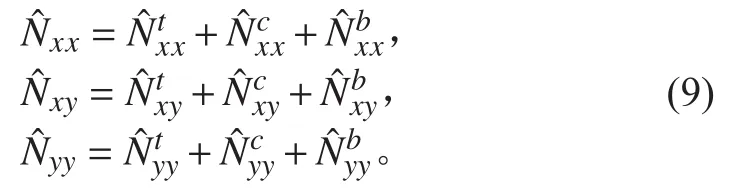
當夾層板受雙軸壓縮載荷時，令

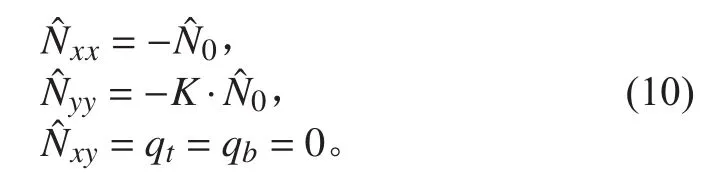
式中：K為載荷系數。若K=0，表示夾層板受單軸壓縮，反之則表示夾層板受雙軸壓縮。

1.4 分析求解

本文采用納維葉（Navier）法求解屈曲問題。在Navier解法中，夾層板的剛度系數應滿足下述條件：

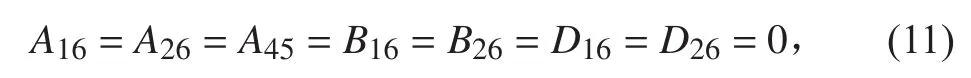
四邊簡支的邊界條件表示為：

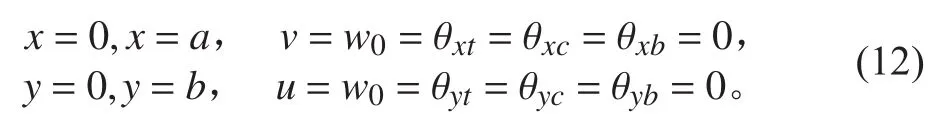
假設矩形SPS夾層板的長為a，寬為b，上下面板的厚度分別為ht和hb，芯材的厚度為hc，基于納維葉解法和位移變量在滿足上述邊界條件下，選取如下雙重三角級數：

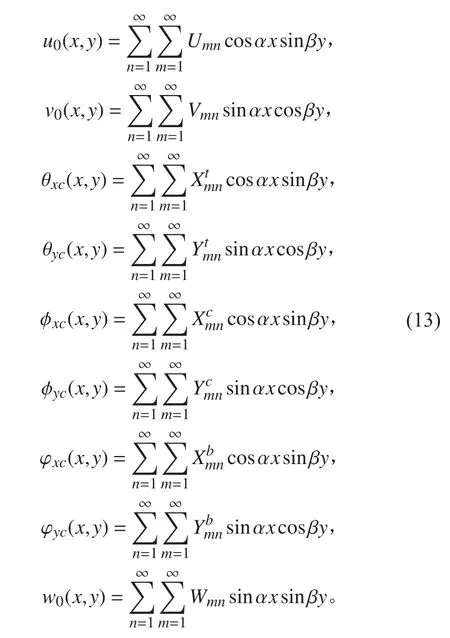
將式（12）代入控制方程式（7）中，得

式中：A為系數矩陣；{X}定義為：

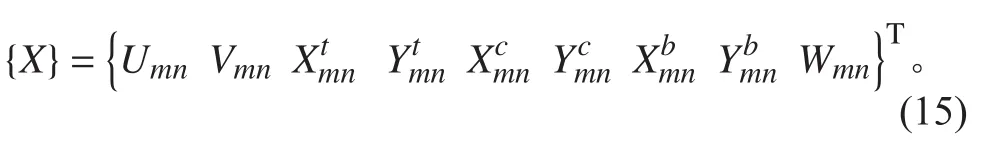
令系數矩陣A的行列式為0，求解可以得到一組特征值以及對應的特征向量。最小的特征值即為屈曲臨界載荷因子，對應的特征向量即為夾層板的屈曲模態。

2 結果與討論

本節使用推導的簡化Zig-zag理論來計算夾層板的總體屈曲載荷。通常情況下，總體屈曲對應的半波數m，n分別為1，如果存在更高的半波數且其對應的屈曲臨界載荷小于總體屈曲載荷時，那么夾層板將發生皺屈等局部失穩現象。

2.1 對比驗證

為了與文獻[17]的結果進行對比，驗證本文理論計算結果的準確性，選取與論文內容相同的結構尺寸和材料參數。即正方形復合材料夾層板，由正交各向異性的層合板面板和各向同性的芯材組成，夾層板的鋪層方式為[0/90/Core/90/0]，面板與芯材的厚度比tc/tf為10，且面板各單層的厚度均相同。夾層板面板和芯材材料參數如表1所示。屈曲臨界載荷的計算結果按式（14）進行無量綱化：

式中：E2為夾層板面板的橫向彈性模量；h為夾層板的總厚度。

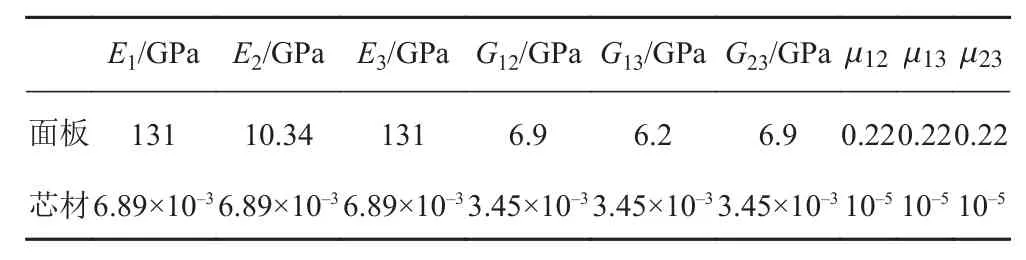
表1 夾層板材料參數Tab.1 Material parameters of composite sandwich plate

無量綱總體屈曲載荷分別由整體-局部高階理論（Global-local high-order theory，簡稱GLHOT）、混合型Layer-wise理論（Mixed layer-wise theory，簡稱MLWT）、Zig-zag理論（Zig-zag theory，簡稱ZZT）、反三角Zig-Zag理論（Inverse trigonometric Zig-zag theory，簡稱ITZZT）、有限元軟件Ansys以及本文簡化的高階Zig-zag理論計算所得列于表2，考慮了不同長厚比（a/h=2，4，10，20，30，40，50，60，70，80，90，100）。

由表1可知，本文計算的結果與混合型Layer-wise理論（MLWT）、Zig-zag理論（ZZT）和反三角Zig-Zag理論（ITZZT）的計算結果相似，最大誤差為8.3%。而整體-局部高階理論（GLHOT）與其他理論的計算結果相比，誤差較大，且預測值整體偏高，這是因為其不能很好的處理夾層板相鄰間的材料性能導致的。表3和圖2分別為夾層板前4階無量綱屈曲臨界載荷及相應的屈曲模態圖。

表2 不同夾層板理論計算無量綱總體屈曲臨界載荷對比Tab.2 Comparisons of the dimensionless overall buckling load for symmetric square sandwich plate

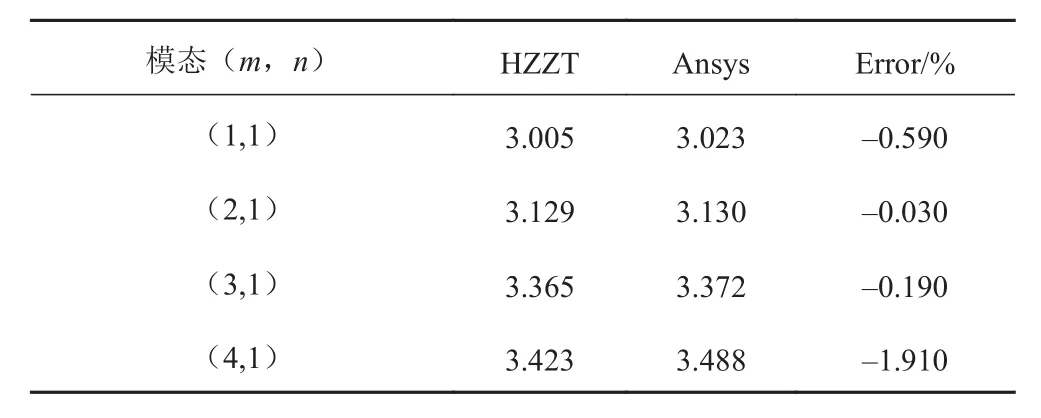
表3 前四階屈曲模態以及對應的無量綱屈曲臨界載荷Tab.3 Buckling mode shapes from the first-order to forth-order and corresponding dimensionless buckling loads

2.2 幾何參數對穩定性的影響

利用本文推導的理論公式結合有限元軟件Ansys研究鋼聚氨酯夾層板的幾何參數對穩定性的影響。面板與芯材的的材料參數取自文獻[22]，其具體值列于表4。

2.2.1 面板厚度對臨界載荷的影響

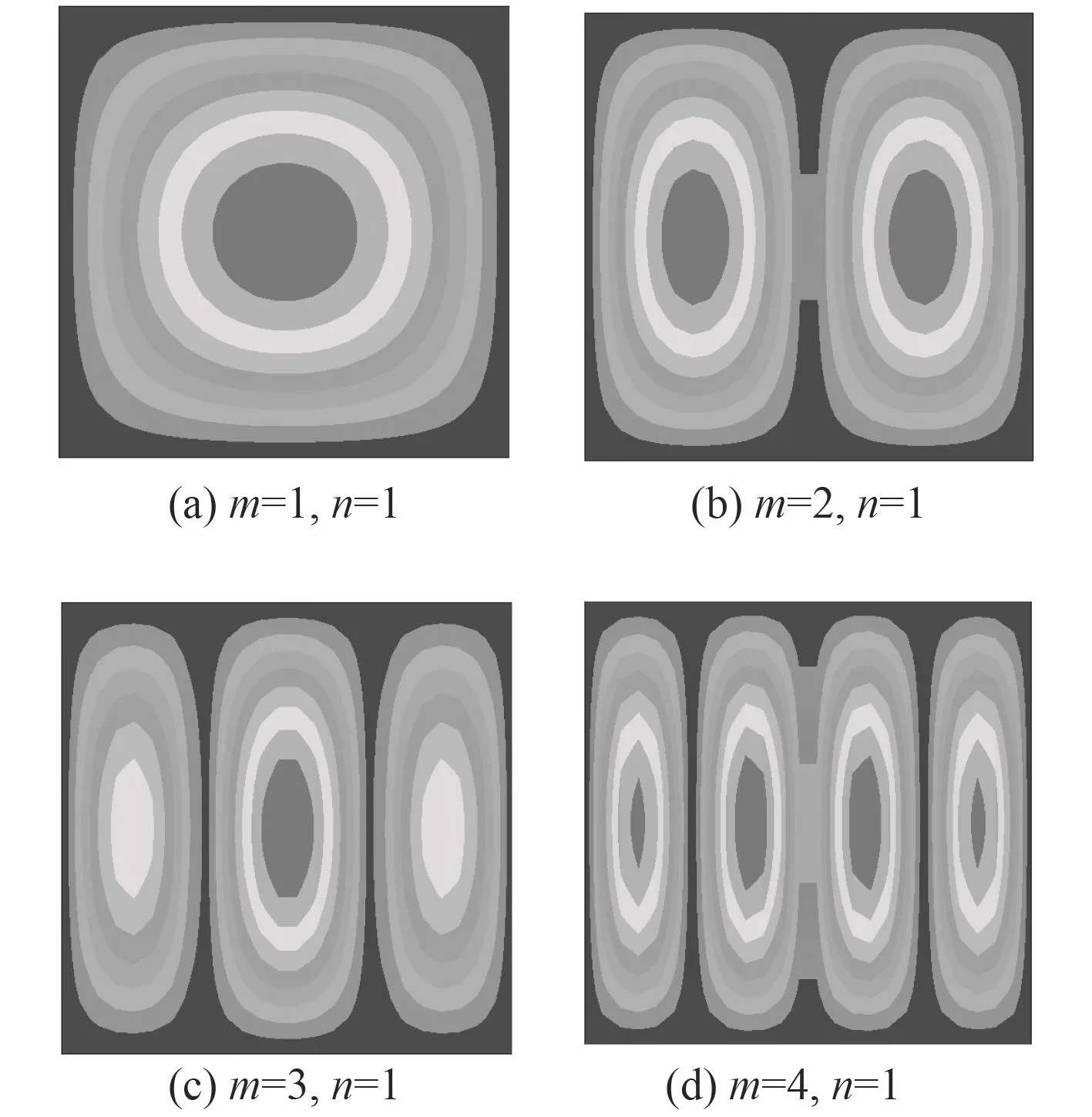
圖2 Ansys計算所得的前四階屈曲模態Fig.2 Contour plots of the buckling shapes obtained by Ansys

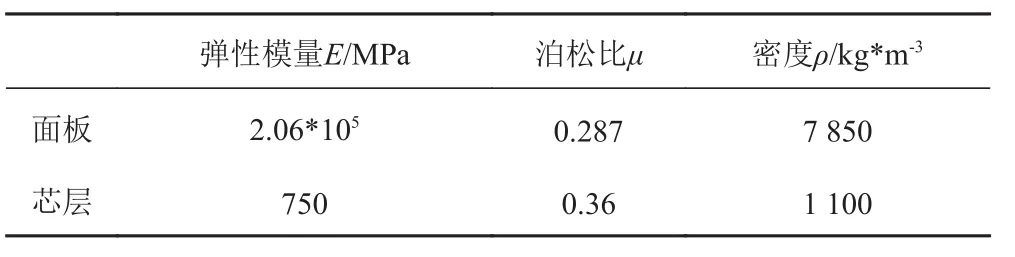
表4 SPS夾層板材料參數Tab.4 Material parameters of SPS sandwich plate

本小節討論不同厚度的面板對SPS夾層板穩定性的影響，以面板厚0.1 mm和芯材厚0.8 mm為基準，分別增重10%，20%，30%和減重10%，20%，30%為條件，得到7種面板厚度，分別為0.147 mm，0.132 mm，0.116 mm，0.1 mm，0.084 mm，0.068 mm，0.053 mm。其中確定參數為：芯材厚度tc=0.8 mm和長寬比a/b=0.5。計算結果列于表5，并且給出了載荷系數K=0和K=1下的屈曲臨界載荷。

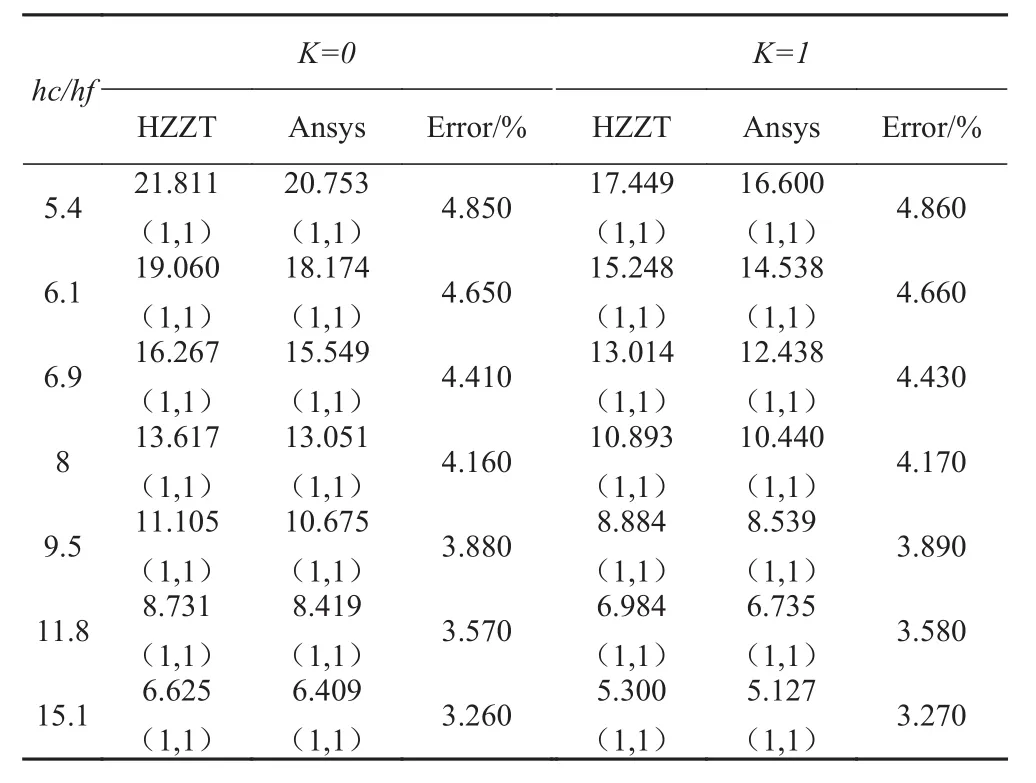
表5 面板厚度不同的夾層板的屈曲臨界載荷對比Tab.5 Comparison of critical buckling load of sandwich plates with differentthicknesses of face-sheet

圖3給出了面板厚度對SPS夾層板的屈曲載荷關系。由圖可知，夾層板的抗屈曲性能隨面板厚度的減少而迅速降低，在曲線的初始階段，夾層板的屈曲載荷的下降速率明顯大于后半段。由于在夾層結構中，面板提供結構的面內剛度和強度，其主要承受由拉壓彎引起的面內拉壓應力和剪切應力，所以當面板的厚度減少時，夾層結構的剛度也相應降低，穩性也隨之降低。

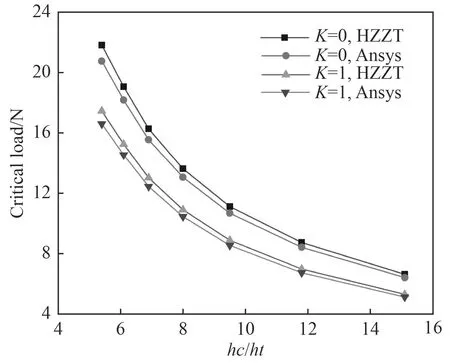
圖3 面板厚度對屈曲臨界載荷的關系曲線Fig.3 Relation curve of face-sheet thickness to critical buckling load

2.2.2 芯材厚度對臨界載荷的影響

本小節討論不同厚度的芯材對SPS夾層板穩定性的影響，以面板厚0.1 mm和芯材厚0.8 mm為基準，分別增重10%，20%，30%和減重10%，20%，30%為條件，得到7種芯材厚度，分別為1.453 mm，1.235 mm，1.018 mm，0.8 mm，0.582 mm，0.365 mm，0.147 mm。其中確定參數為：面板厚度tf=0.1 mm和長寬比a/b=0.5。計算結果列于表6，并給出了載荷系數K=0和K=1下的屈曲臨界載荷。

圖4為芯材厚度對SPS夾層板屈曲載荷的關系圖。由圖可知，夾層板屈曲臨界載荷隨著芯材厚度的增加而增加。這是因為在夾層結構中，夾層板的彎曲剛度受面板性能和上下面板之間高度的影響，當芯材厚度增大時，意味著增加了上下面板之間的高度，導致結構的彎曲剛度得到加強，自然抗失穩的能力也就增強。

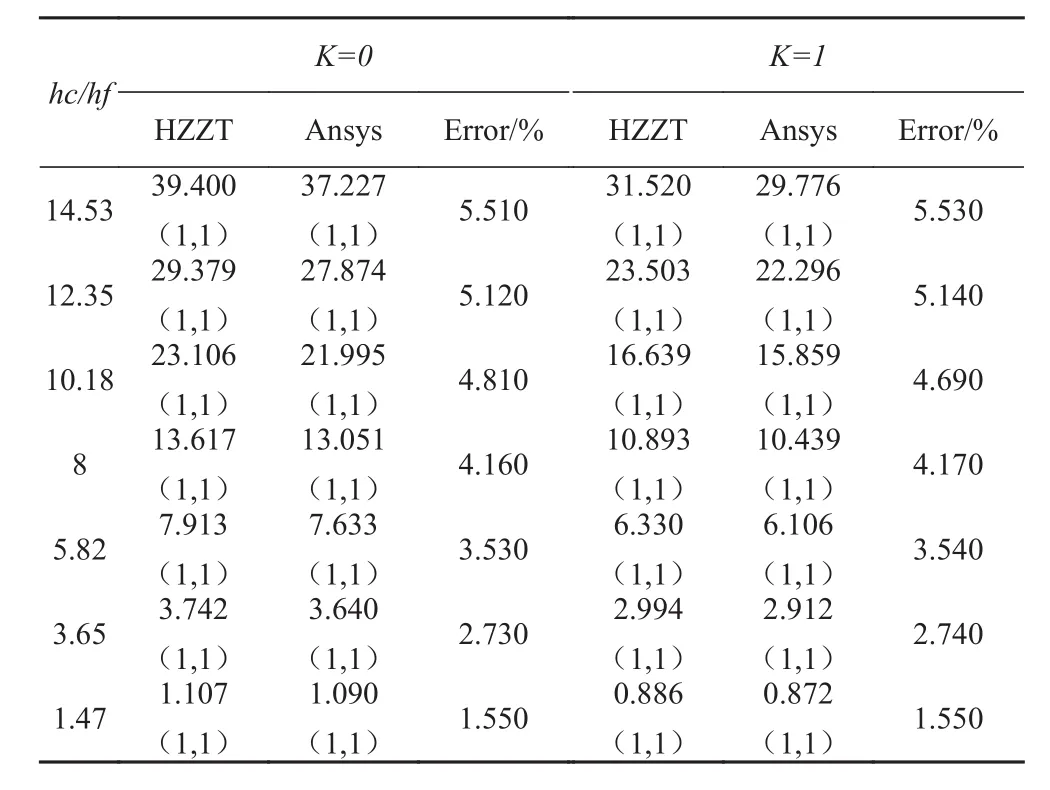
表6 芯材厚度不同的夾層板的屈曲臨界載荷對比Tab.6 Comparison of critical buckling loads of sandwich plate with different core thicknesses

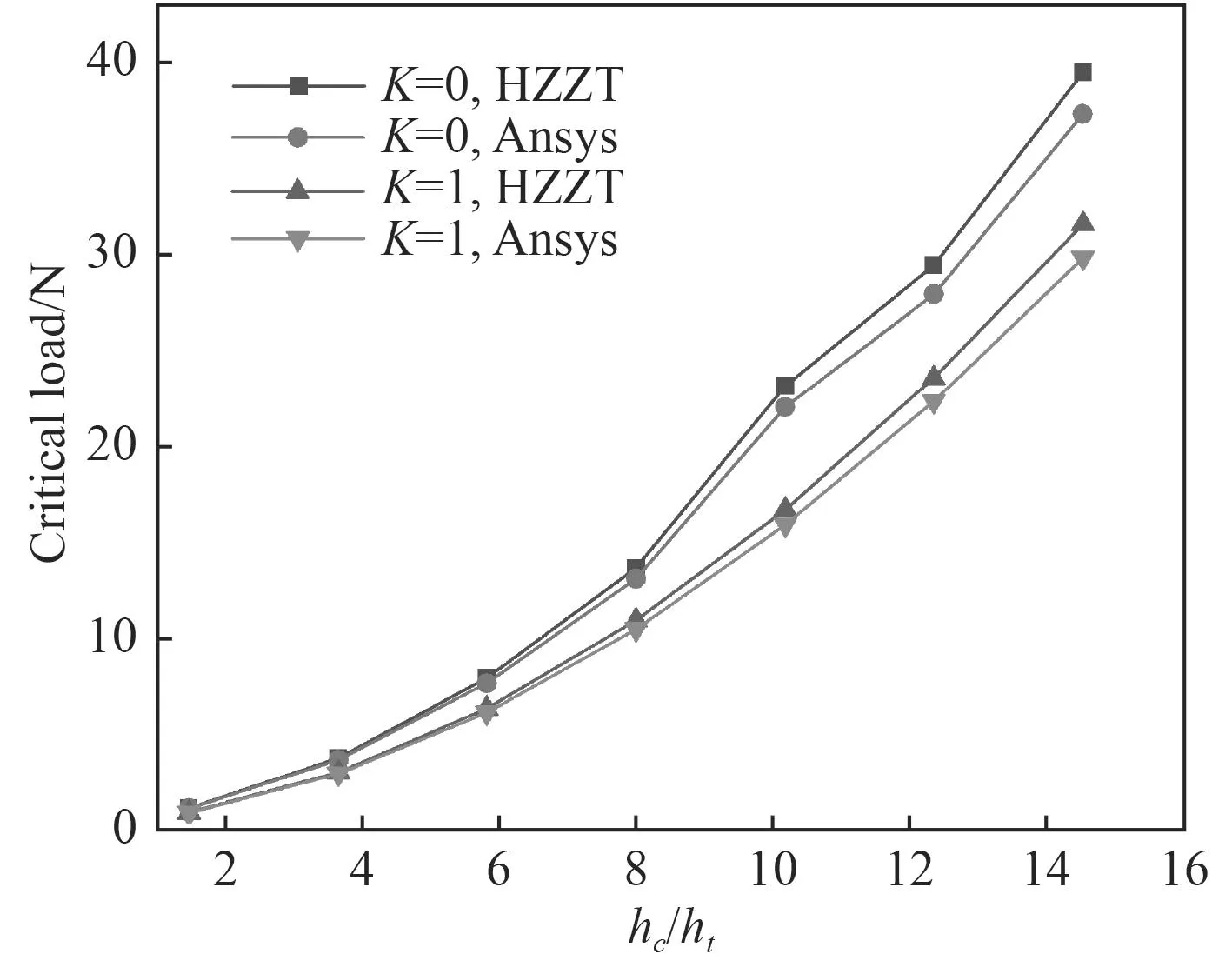
圖4 芯材厚度對臨界屈曲載荷的影響關系曲線Fig.4 Relation curve of core thickness to critical buckling load

圖5描述了在質量增比相同的情況下面板與芯材厚度對SPS夾層板屈曲載荷的影響。由圖可知，當結構總質量每增加10%時，芯材厚度對SPS夾層板穩定性的影響更加敏感。因此，在考慮SPS夾層板質量的前提下，若想快速提高SPS夾層結構的穩性，宜優先增加芯材即聚氨酯的厚度。

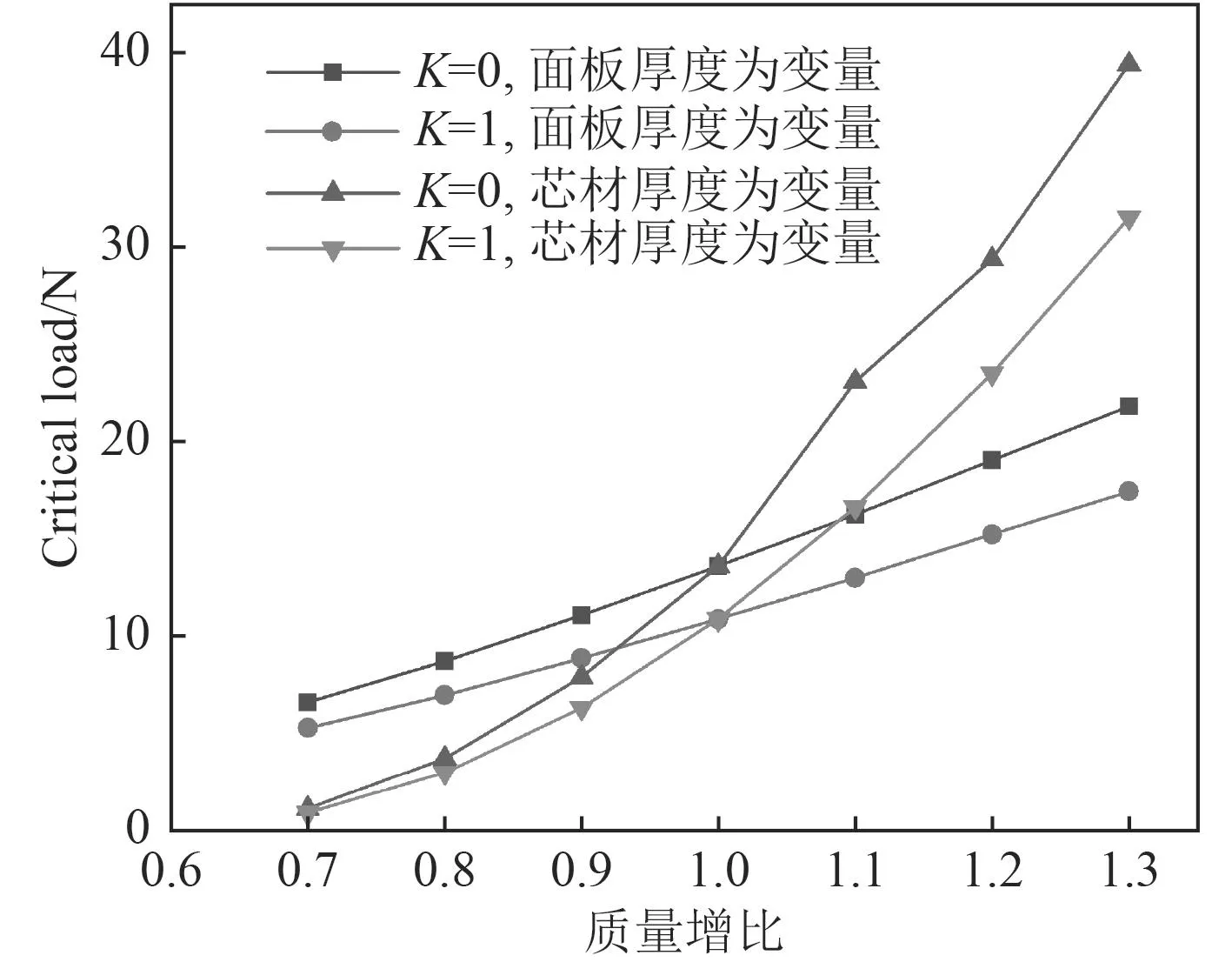
圖5 不同質量增比下，面板和芯材厚度對屈曲載荷的影響關系曲線Fig.5 Influence curves of face-sheet and core thickness on critical buckling load at different mass increasing ratios

3 結 語

本文首先建立簡化的高階Zig-zag數學分析模型，在該模型中面板采用一階剪切變形理論，芯材采用Reddy高階剪切變形理論，在滿足各項連續條件的前提下，選用納維葉（Navier）法求解簡支板的屈曲臨界載荷。然后重點討論了幾何參數對SPS夾層板穩定性的影響，并輔以有限元軟件Ansys作為對比，可以得出以下結論：

1）本文理論計算的總體屈曲臨界載荷與其他理論計算方法吻合度較高，說明本文方法的合理性和準確性。

2）板厚對SPS夾層板的穩定性影響較大，當考慮結構的質量時，增加芯材（聚氨酯）的厚度更能提升結構的抗屈曲性能。