引信裝定系統用模擬火控系統設計

魏亞偉，李豪杰，原紅偉，于 航

(南京理工大學 機械工程學院，南京 210094)

新形勢下戰爭不再是單一的某一個作戰單元發揮作用去攻擊敵方，而是與其他的作戰平臺交聯成一個整體，實現信息交互[1-3]。其中，火控系統包括了武器系統中絕大部分的電子設備，也承載了武器系統中的通信控制、目標識別與跟蹤、炮車控制、鏡體控制、定位導航和傳輸顯示等許多主要和關鍵的作戰任務，是武器系統交互控制的匯聚點和核心，是武器現代化的標志[4]。而引信與火控系統之間的互聯對攻擊來襲目標或者殺傷敵方起到關鍵作用，通過在發射前、發射過程中、發射后對引信的裝定，使得引信適時作用在最理想的時間、距離、方位引燃、引爆戰斗部裝藥從而使彈藥戰斗部起到最大的殺傷效果，實現最佳的作戰模式[5]。由于火控系統是發射平臺的一部分，對于從事信息化引信研究的人員在研究信息交聯時無法脫離火控系統實現獨立測試與性能驗證[6-7]。通過查閱資料，文獻[8]提出了基于二維插值算法的引信用裝定器彈道參數解算方法，滿足精度的同時，也簡化了計算，但是該方法運算速度慢，占用內存大，對射表的使用較復雜。文獻[9]提出了當前軍機廣泛的使用指令響應型數據總線作為其多功能綜合航空電子火控系統的數據傳輸和控制系統，并進行了仿真，但沒有編寫相應的上位機來滿足實驗室裝定的需求。在編寫人機交互界面的過程中，MATLAB強大的計算能力和界面設計功能使其成為主要的設計工具[10-11]。為此，通過對火控系統的分析，明確了實驗室裝定引信對火控系統解算信息，實時裝定功能的需求，基于MATLAB軟件，采用整體擬合法的數據處理手段，對導入的射表進行擬合，在輸入外部環境信息的情況下，解算出裝定信息，編寫相應的人機交互界面程序來實現模擬火控的功能。

1 模擬火控系統設計

1.1 模擬火控系統的構成

引信裝定系統用模擬火控系統需完成射表轉換，參數輸入，裝定數據解算等三項功能。首先導入射表，然后通過輸入炸點距離、海拔、氣溫、氣壓、風速、風向時可以得到引信預裝定時間TPE1和速度修正系數K；最終把信息傳送給裝定器，裝定器裝定信息到引信。其中模擬火控系統為本文主要設計部分，并且滿足炸點距離900 m的范圍內，裝定飛行時間誤差小于1 ms,裝定速度修正系數誤差小于0.01 ms/(m/s)，其模擬火控裝定工作流程框圖如圖1。

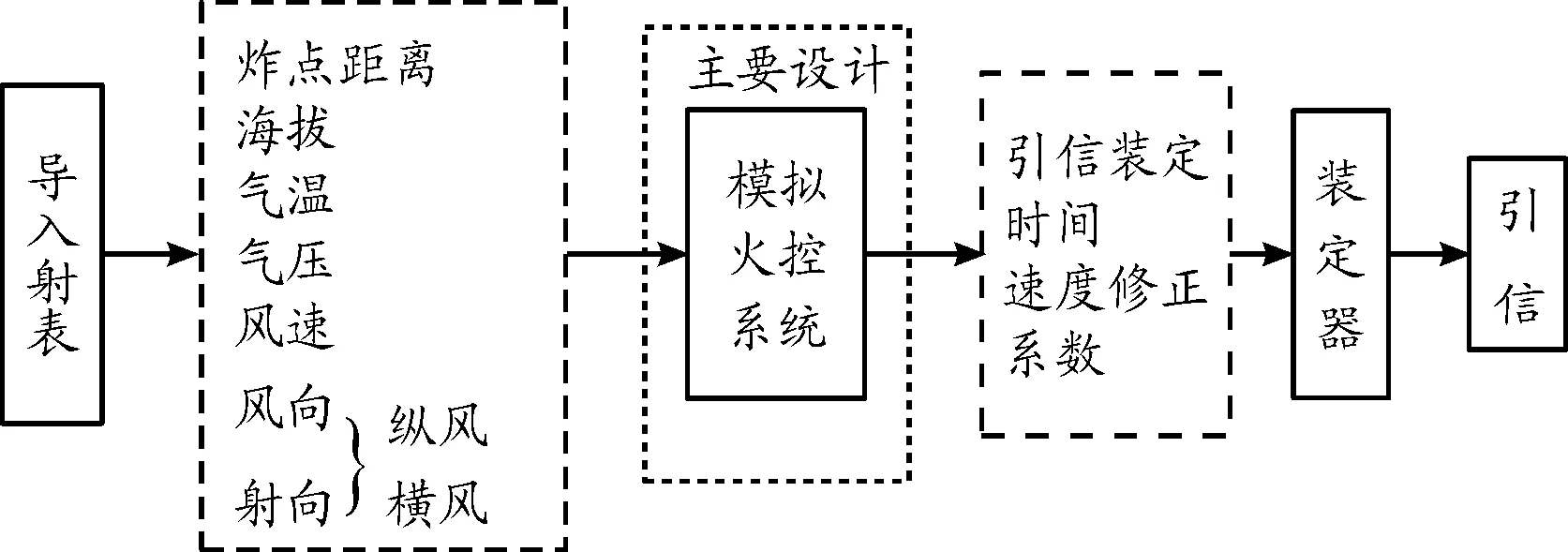
圖1 模擬火控系統裝定工作流程框圖

而在系統程序中要包括對氣溫、氣壓的修正系數運算過程、縱風、橫風風速的修正系數運算過程、速度修正系數的運算過程。

1.2 射表修正量使用方法

本文導入的射表即表1和表2，其中表1為某定距彈的飛行時間和速度修正系數與炸點距離的關系，表2反應了外部環境條件變化導致的裝定時間變化量與炸點距離的關系。

表1 某定距彈基本射表

表2 某定距彈修正量表

引信裝定系統用模擬火控系統最終輸出計算結果有兩個：一個是速度修正系數K，另一個是引信預裝定時間TPE1。

引信預裝定時間TPE1的計算式：

TPE1=T(L)+0.001E

(1)

式中：T(L)為射表中所列出對應射程L的飛行時間，查表1。時間單位(s)；E為射程L的時間修正量。時間單位(ms)。

時間修正量E的計算公式：

(2)

式中：Ki為對應修正系數；Δi為對應偏差量。

1.3 系統總體設計及程序流程圖

在1.1節中明確說到引信裝定系統用模擬火控系統的基本構成，由輸入部分、控制部分、輸出部分、其他部分組成。其中輸入部分包括射表的導入，炸點距離，海拔及相關環境條件變化等信息；控制部分即為內部射表的擬合計算和裝定給引信數據的解算；輸出部分為解算數值的輸出顯示；其他部分為模擬火控系統標題的美化顯示。

系統的總體在滿足上述必須部分的基礎上，盡可能簡潔明了容易操作。根據設計要求和系統構成編輯出如圖2所示界面，滿足設計要求。

圖2 引信裝定系統用模擬火控系統界面

通過編寫程序，實現上述界面的各個模塊功能，運行程序的流程框圖如圖3。

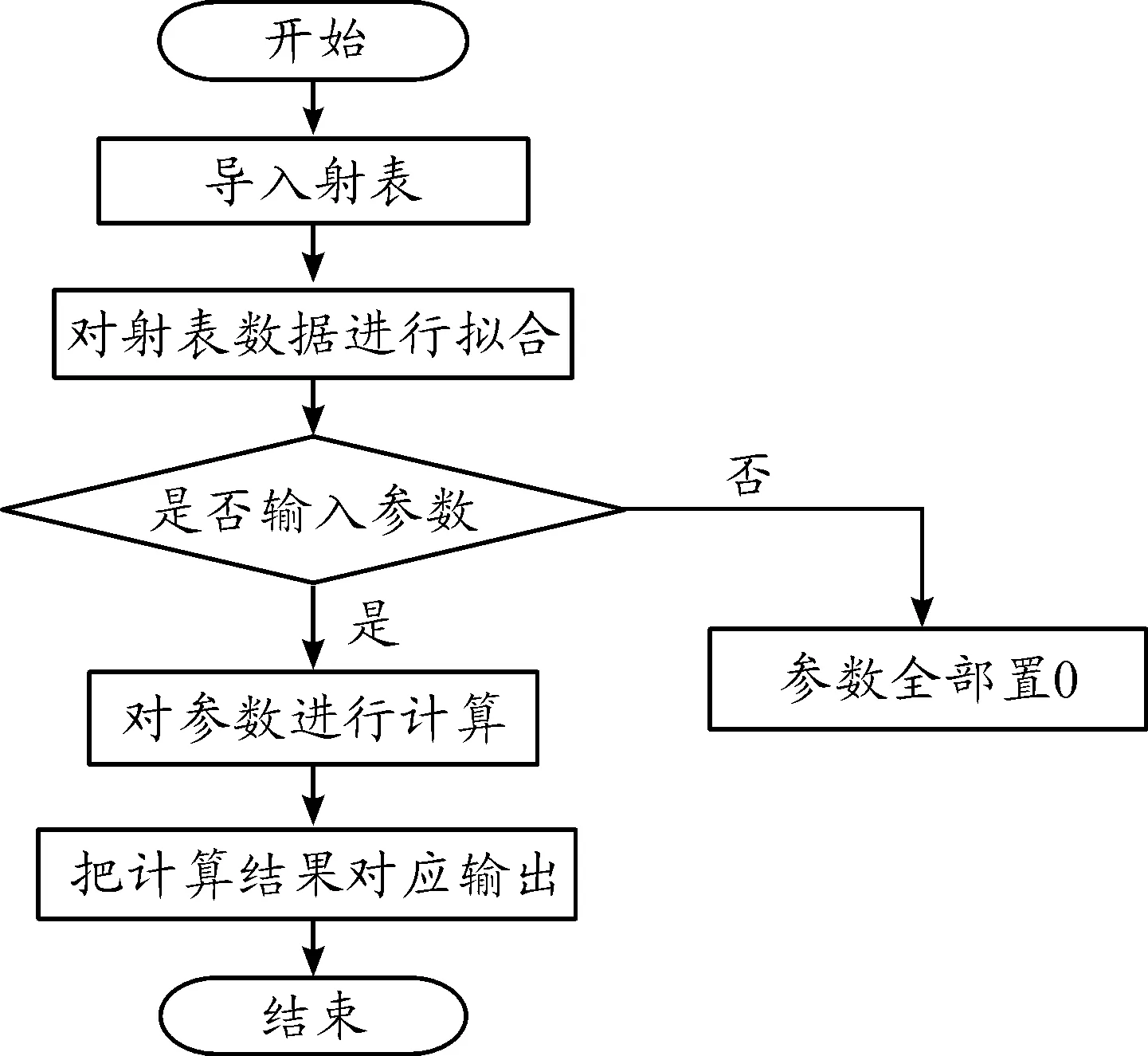
圖3 模擬火控的程序流程框圖

2 模擬火控的射表數據擬合

采用擬合法進行系統設計，是將射表導入到Matlab中，利用Matlab強大的計算能力，對導入的射表進行繪圖，并對圖像進行擬合，得到整體擬合公式，以下是對飛行時間、速度、氣溫、氣壓、橫風、縱風等修正系數的擬合圖像，并得到相關的擬合公式。其中氣壓、橫風、縱風與前面圖像類似，進行省略。

其公式如下：

1)飛行時間二次方擬合公式：

y=3.397 4e-08*x2+0.000 656 97*x+7.046 6e-5

其擬合圖像如圖4所示。

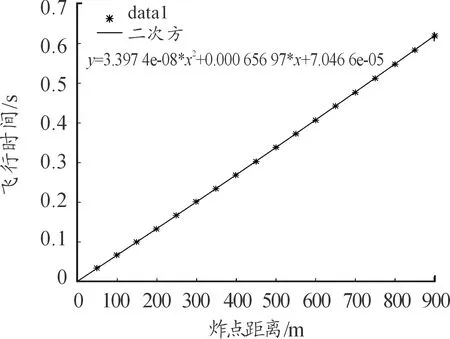
圖4 飛行時間二次方擬合圖像

2)速度修正系數二次法擬合公式：

y= -6.453 8e-08*x2-0.000 860 16*x+0.000 621 32

其擬合圖像如圖5所示。

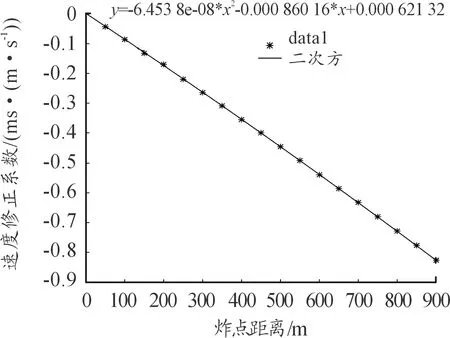
圖5 速度修正系數二次方擬合圖像

3)氣溫修正系數二次方擬合公式：

y= -9.151 2e-07*x2+4.500 8e-05*x-0.004 436 3

其擬合圖像如圖6所示。

3 模擬火控試驗驗證

根據射表中的數據(表1)，某定距彈在海拔高為340 m，氣溫變化5 ℃，氣壓變化500 Pa，無橫風和縱風的情況下，模擬火控解算的裝定數值如表3所示。

圖6 氣溫修正系數二次方擬合圖像

表3 模擬火控裝定數值

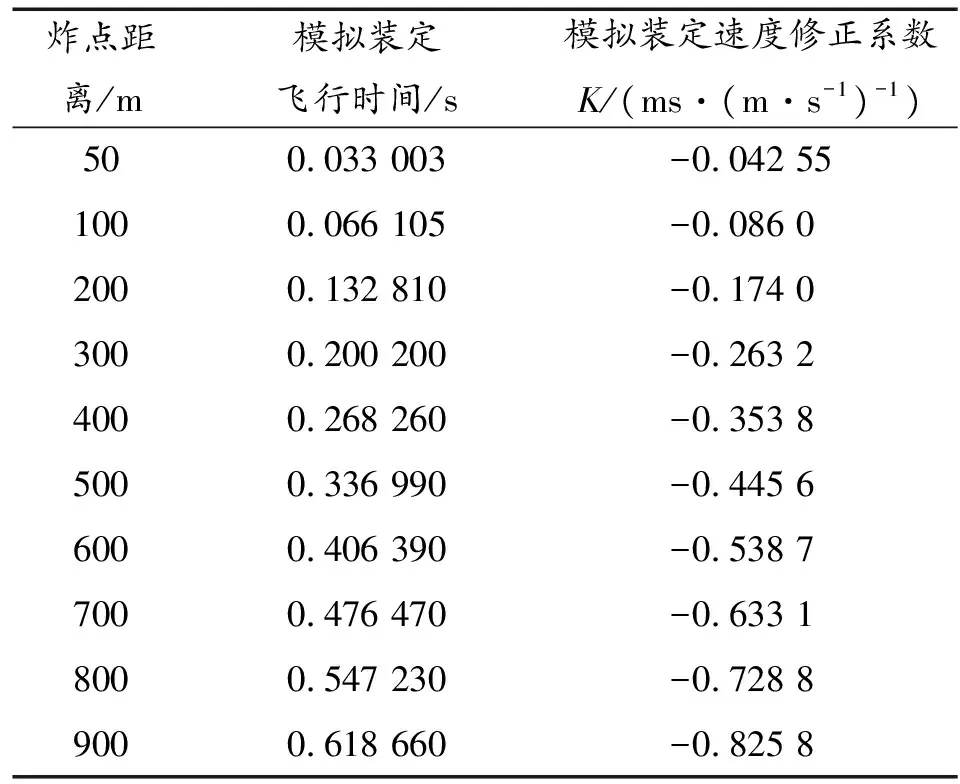
炸點距離/m模擬裝定飛行時間/s模擬裝定速度修正系數K/(ms·(m·s-1)-1)500.033 003-0.042 551000.066 105-0.086 02000.132 810-0.174 03000.200 200-0.263 24000.268 260-0.353 85000.336 990-0.445 66000.406 390-0.538 77000.476 470-0.633 18000.547 230-0.728 89000.618 660-0.825 8

與射表內的裝定數值相比，其絕對誤差如圖7所示。

圖7 模擬火控裝定量的絕對誤差示意圖

由圖7可知，在900 m的炸點距離內，裝定時間的絕對誤差最大為0.053 ms,小于1 ms,速度修正系數絕對誤差小于0.01 ms/(m·s-1)，在誤差允許的范圍內，模擬火控的裝定數值可滿足測試功能與性能要求。

4 結論

本文為實現引信裝定功能的實驗室測試，在明確模擬火控系統設計需求的情況下，開展了模擬火控的功能分析與設計，并設計了模擬火控人機交互界面。基于工作流程分別設計各子系統程序模塊。

子系統采用擬合法進行設計，通過對射表數據進行擬合計算，得到與炸點距離相關的函數，在數據處理時計算量少、滿足精度要求。通過模擬火控試驗驗證，誤差小，精度符合裝定要求，為實驗室可裝定引信的設計和測試帶來了極大便利。