不同結構射彈高速入水穩定性分析

黃鴻鑫,張會鎖,魏 錦，張 帆

(1.中北大學機電工程學院，太原 030051；2.中國船舶重工集團公司第七一三研究所，鄭州 450000)

射彈高速入水及其穩定性研究仍是國內外一大熱點和難題，尚有許多理論、數值模擬以及實驗等方面的難題需要解決[1]。射彈高速入水穩定性理論研究主要有以下三個方面：

一是射彈高速入水超空泡發展過程研究。G.V.Logvinovich等[2]描述了空泡截面獨立擴張原理對空泡發展過程；Tadd T Truscott等[3]對高速傾斜入水空泡形態和空泡發展過程進行了研究；M.Lee等[4]利用能量守恒原理對射彈高速入水空泡生成、發展過程及閉合特性進行了研究；Michael Dean Neaves等[5]在Euler方程的基礎之上，通過引入自然超空化計算模型和Tait狀態方程，對射彈高速垂直入水時的空泡形態和發展過程進行了數值模擬；秦楊等[6]對超空泡射彈高速傾斜入水的空化流動進行了數值模擬；王瑞琦等[7]對不同頭型彈丸低速垂直入水開展了實驗研究。

二是射彈高速入水沖擊與水動力研究。王永虎等[8]對不同頭型彈體的入水沖擊力進行了研究；王冰等[9]提出了耦合非線性自由液面的方法仿真計算入水問題。

三是射彈入水穩定性影響因素研究。王澤宇[10]應用FLUENT軟件VOF模型開展了射彈帶攻角和旋轉過程的數值模擬；張偉等[11]開展了35～160 m/s速度下的入水實驗，研究了3種不同頭型射彈入水過程的穩定性。

目前，國內外對于入水空泡形態的發展過程和入水沖擊及水動力的研究較為深入，而對入水穩定性影響因素的研究相對較少，尤其對于射彈速度大于200m/s入水穩定性影響因素的研究更少，射彈的高速入水給試驗研究造成了很大的困難，因此采用理論分析和數值模擬成為解決該類問題最有效的手段。本文將通過有限元分析軟件ABAQUS/Explicit，建立射彈高速入水有限元模型，針對射彈的頭部形狀和射彈的質心位置對射彈高速入水穩定性影響展開分析研究，從空泡形態、速度衰減以及俯仰角變化這個三個方面來考察射彈入水后彈道穩定性。

1 入水模型正確性驗證

1.1 有限元模型建立及材料設置

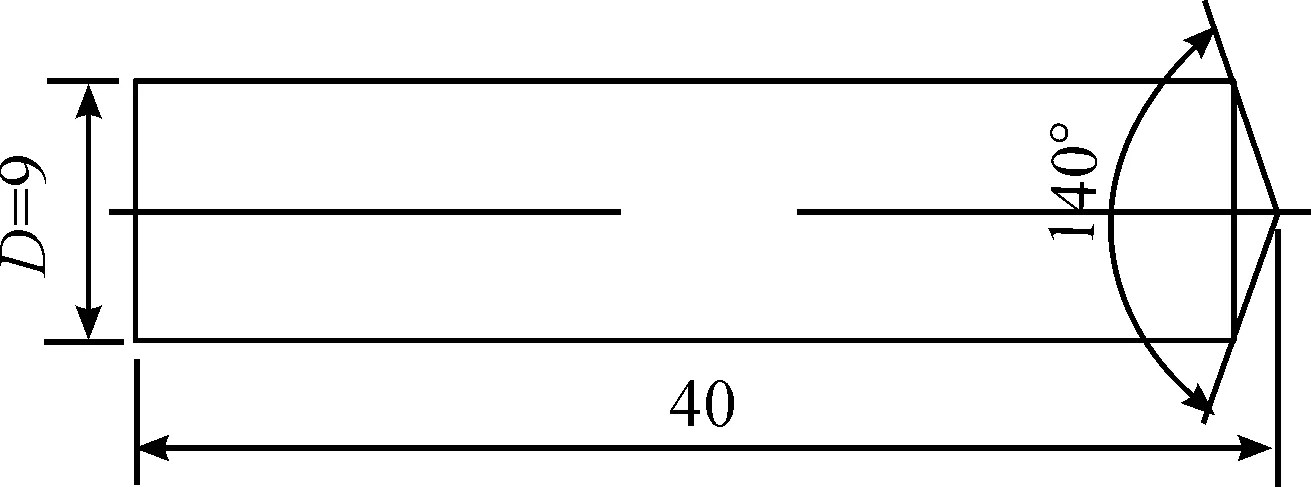
圖1 入水物體模型示意圖

空氣和水材料模型為ABAQUS中的Us-Up狀態方程，空氣和水材料模型參數如表1所示，線性Us-Up Hugoniot形式的Mie-Gruneisen狀態方程[14]來描述水介質的體積響應，其常用形式為：

p-pH=Γρ(Em-EH)

(1)

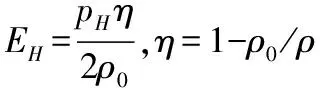
(2)

表1 空氣和水材料參數

常用的對材料雨貢紐曲線擬合關系為：

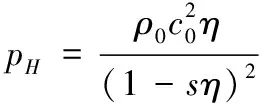
(3)

式(3)中，c0、s為定義線性沖擊波波速Us、粒子速度Up關系的系數。其關系為：

Us=c0+sUp

(4)

進而得到線性Us-Up Hugoniot形式的Mie-Gruneisen狀態方程，其表述為：

(5)

由于彈丸在入水過程中不會出現明顯變形[13]，因而，在不影響計算結果準確性的前提下，為了提高計算效率，將彈丸設置為ABAQUS中的離散剛體，定義其密度、彈性模量值和泊松比如表2所示。

表2 射彈材料參數

1.2 計算結果對比分析

圖2為試驗與數值模擬的空泡形態結果，空泡的整個發展歷程經歷了從運動體撞擊水面后空泡流動的形成、空泡充分發展、空泡壁面擴張到最大直徑后開始閉合到最后空泡完全閉合的整個過程，且試驗結果與數值模擬結果吻合較好，說明本文所采用的有限元模型時準確可靠的。

從圖2中t=12 ms可以看出，在模型頭部撞擊水面以后，在水面以上形成一層水幕，即噴濺[15]。隨著時間的推移，噴濺先是向上和向外迅速運動，當向外擴張速度減小到零時開始向中間收縮，最后在入水點上方匯聚到某一點，并形成一個拱形圓頂，如圖2中t=55 ms時刻所示。

圖2 試驗結果與數值模擬結果

2 射彈結構對入水穩定性影響分析

2.1 有限元模型建立

為了研究射彈結構對入水穩定性的影響，將設計幾種不同結構的射彈模型以400 m/s入水速度和30°入水角度進行數值模擬，空氣、水和射彈的空間相對位置如圖3所示。射彈結構包括射彈的質心位置和射彈的頭部形狀，其中質心位置是質心距離彈頂的距離。為了保證射彈在相同質量的條件下質心位置不同，本文將射彈內部進行挖空，通過調整空穴的位置以達到相同質量的射彈、質心位置不同的目的。不同射彈的結構示意圖如圖4。

圖3 空氣、水和射彈的空間相對位置示意圖

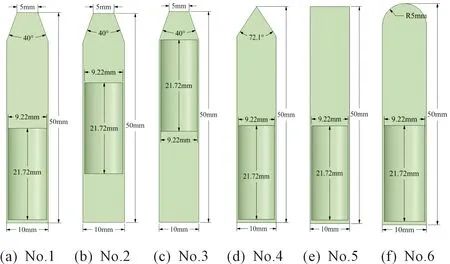
圖4 不同結構射彈示意圖

共設計了4種不同頭部形狀的射彈，分別為截錐形、錐形、圓柱形以及半球形，射彈參數如表3所示。在不影響觀測空泡發展的前提下，將水域和空氣域設計成斜置長方體形狀如圖5所示，斜置角度為射彈的入水角度，其尺寸與空泡發展過程中的最大尺寸相近，目的是為了省去計算域中不必要空間的網格數量，以提高網格利用率。同時為避免模型邊界影響計算結果，在水域和空氣邊界上施加無反射邊界。

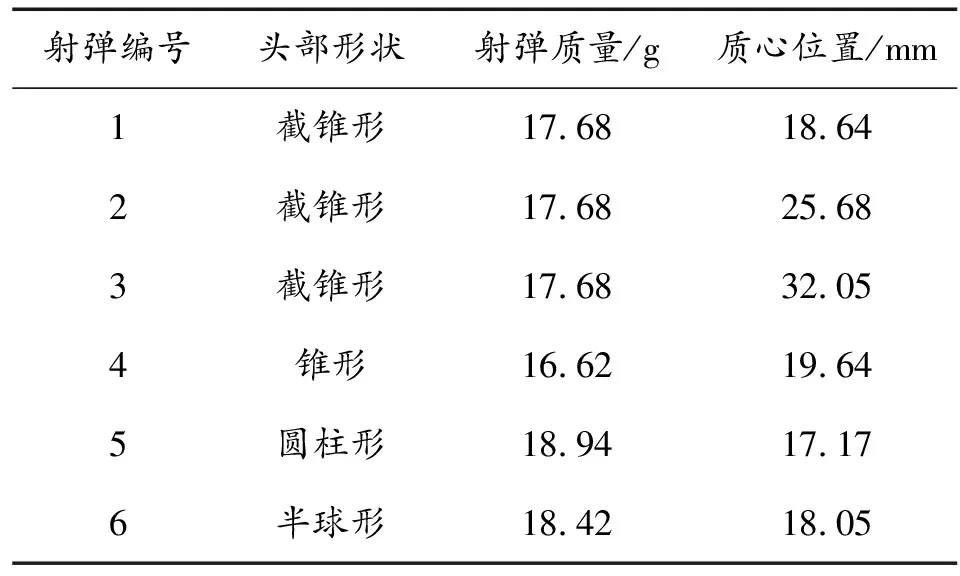
表3 不同結構射彈參數

2.2 數值模擬結果

圖5給出了6種不同結構射彈入水過程，射彈入水過程經歷入水沖擊、空泡形成、開空泡3個階段[16]。由于射彈是以30°入水，噴濺具有明顯的不對稱性如圖5(a)所示，產生不對稱現象的主要原是因為射彈具有較高的水平方向的速度分量，導致射彈與水面接觸附近的流體時獲得了較大的沿水平方向的動量。各射彈的入水初期姿態具有較好的一致性，但隨著入水過程的繼續進行，4號和6號射彈姿態發生了較大變化，彈軸幾乎與水平軸平行，最終水下彈道徹底失去穩定，導致失去穩定性的主要原因錐形和球形在空泡形成階段形成的空泡最不理想，使得射彈在入水初期就發生了強烈尾拍[17]，從而使得入水彈道出現了不穩定現象。

除去4號射彈和6號射彈入水不穩定之外，1號、2號、3號射彈和5號射彈穩定性較好，但1號、2號和3號射彈都發生輕微的尾拍，使得空泡壁面產生了上下不對稱現象，射彈的質心位置是影響射彈尾拍的重要因素。質心位置靠前的1號射彈，首先與空泡的下壁面發生了尾拍，隨著運動的繼續又與上壁面發生了尾拍，如圖5(a)所示；2號射彈也首先與空泡下壁面發生了尾拍作用，但未與空泡上壁面發生尾拍，如圖5(b)所示；3號射彈與空泡上壁面發生尾拍，尾拍后彈軸方向持續向下未且未與下壁面發生尾拍，如圖5(c)所示；而5號射彈入水穩定性最佳，整個入水過程未發生尾拍，空泡上下壁面具有良好的對稱性，如圖5(e)所示。

根據圖6(a)可以看出，1號、2號和3號射彈合速度衰減基本一致，速度衰減最快是入水穩定性最差的4號和6號射彈，原因是由于彈道不穩定，使得整個彈體完全處于浸濕狀態，阻力大大增加；而5號射彈雖有良好的入水穩定性，但其入水后的速度衰減也很大，說明5號射彈在水中運動時受到的阻力最大。圖6(b)～圖6(d)為射彈入水后的速度分量，圖6(d)體現了射彈在水下運動時的偏航速度，其中偏航速度變化最大的是4號射彈和6號射彈，也說明4號射彈和6號射彈的入水后運動時是存在偏轉運動的；偏航速度幾乎零的1號射彈和5號射彈。

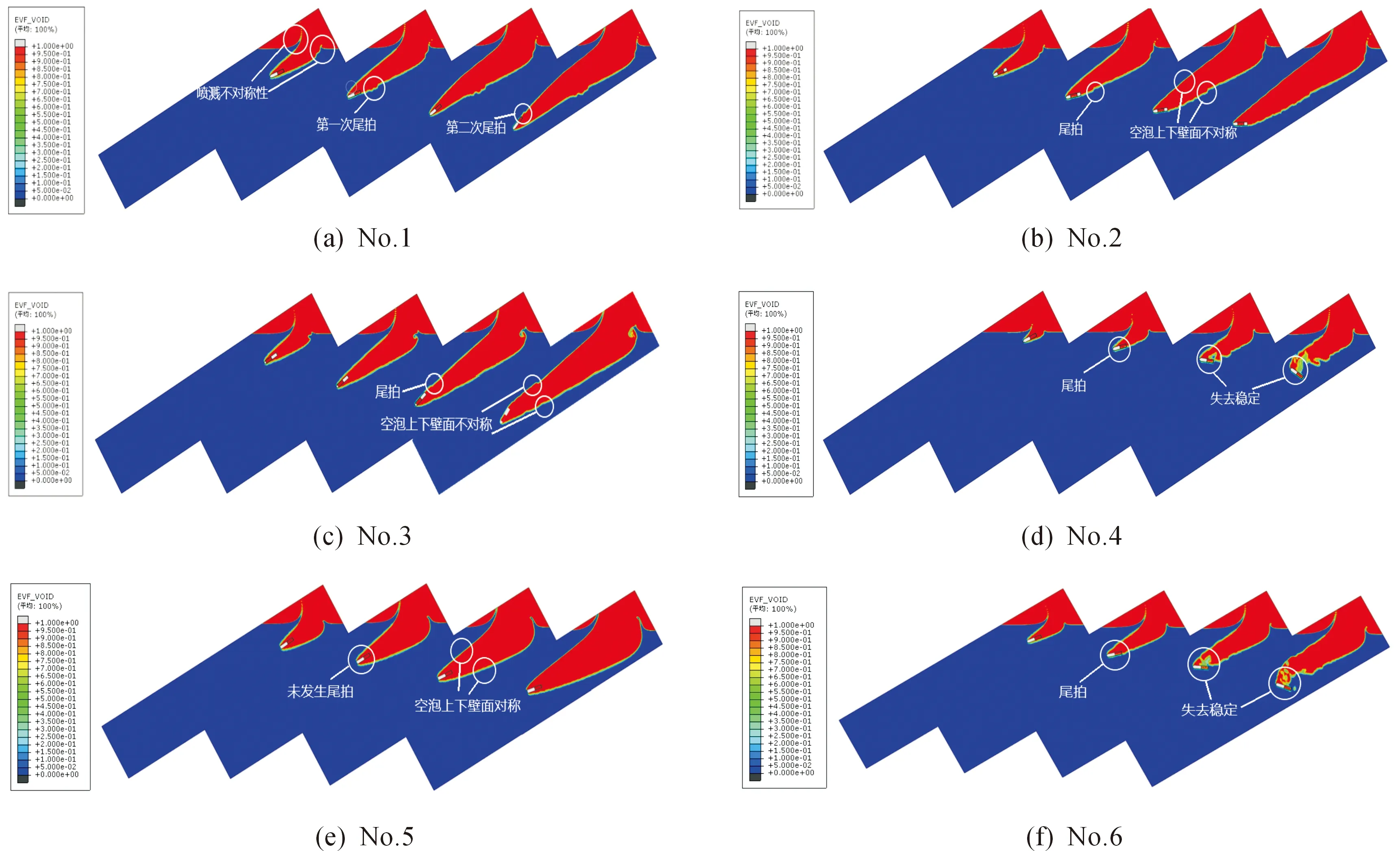
圖5 不同結構射彈入水過程

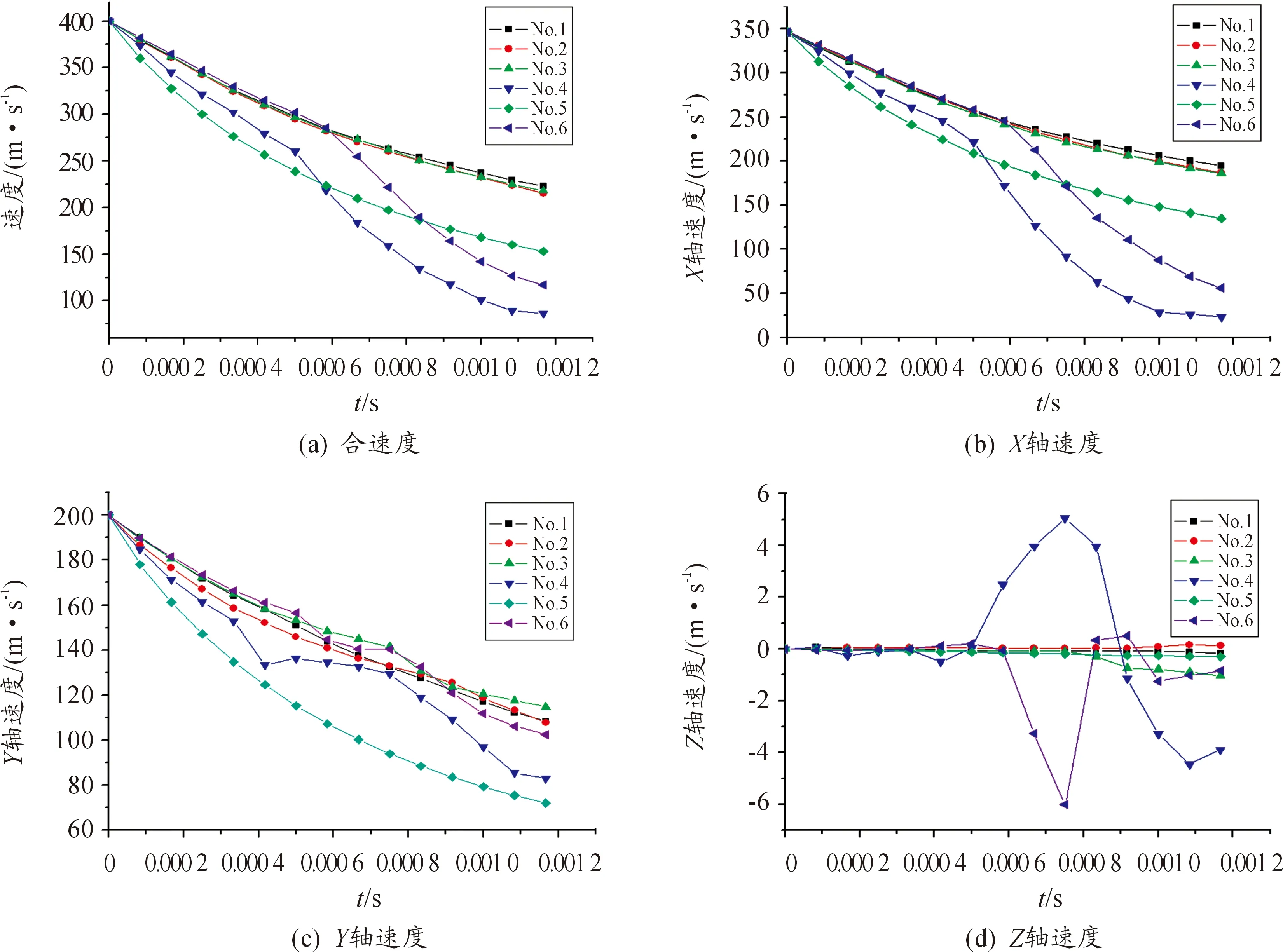
圖6 射彈入水速度隨時間變化曲線

忽撲是決定射彈水下運動軌跡的重要因素[18]，忽撲實際上就是射彈入水后的俯仰角變化，忽撲影響射彈在入水空泡中的位置，從而很大程度上決定了水下運動軌跡將是下向上彎曲、向下彎曲或是直的，本文俯仰角是正值時表明運動軌跡是向上彎的，負值反之，圖7給出了各個射彈的俯仰角隨時間變化曲線。由于4號射彈和6號射彈入水的不穩定性，其俯仰角變化最大且為正值如圖7(b)所示，說明4號射彈和6號射彈的運動軌跡是嚴重向上彎曲的。俯仰角變化幅度最小的是1號射彈，從圖7(a)中可以看出，1號射彈的兩次尾拍造成了俯仰角先正后負。

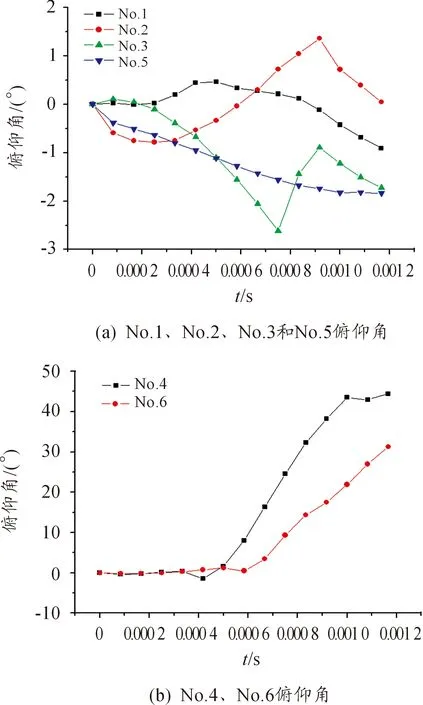
圖7 射彈俯仰角隨時間變化曲線

綜合對比了6種不同結構射彈的水下運動空泡(如圖5)、速度隨時間變化(如圖6)和俯仰角變化(如圖7)，可以得出：對于高速入水射彈，頭部形狀為錐形和半球形的射彈不利于入水穩定，平頭射彈有利于入水穩定，但射彈頭部直徑過大時，會增大水中的運動阻力，使得速度衰減加快；質心靠前的射彈雖然會增加射彈尾拍次數，但不會出現俯仰角持續處于負值或正值的情況，俯仰角的值會處于0°附近上下波動。

3 結論

1)頭部形狀為圓柱形頭和截錐形的射彈入水穩定性良好，而錐形和半球形入水穩定性較差，若想提高射彈入水穩定性應多采用平頭彈進行設計；

2)質心距離彈頂較遠時忽撲現象較為嚴重，且射彈的俯仰角會持續處于正值或負值；質心距彈頂較近時有利于提高射彈的入水穩定性，但質心過于靠前會增加射彈的尾拍次數。