基于CTDEA算法的車輛+UAV配送路徑優化

韓 明,王亞彬，丁連永，王添幸

(1.陸軍工程大學石家莊校區，石家莊 050003；2.32653部隊，沈陽 110163;3.國防大學聯合作戰學院，石家莊 050084)

維修保障主要以搶救搶修為主[1]，在未來信息化精確打擊的對決下，武器裝備維修器材需求隨機性大、位置分散，這對配送的機動能力和時效性提出了更高要求。特別是中印邊境高寒山地地區，主戰場位于狹長通道，山高谷深、地形復雜；交通設施條件落后；冰凍、雪崩等多發惡劣天氣易阻斷投送路線；有效保障時間有限(下午4、5點至半夜持續風沙不能進行維修操作)；車輛性能下降(發動機功率下降30%，載重量下降25%)，故障高發；有生力量非戰斗減損嚴重，單兵力竭運動易產生急性腎損傷、炎癥反應和雪盲。這導致高原山地車輛行速度緩慢，行駛范圍受限，基本依靠人力進行“最后一公里”的末端配送，嚴重制約我軍維修器材的配送效率。

由Dantzig于1959年提出的車輛路徑優化問題(Vehicle Routing Problem,VRP)是典型的NP難問題。其變體問題——帶時間窗的車輛路徑規劃問題(Vehicle Routing Problem with Time Window,VRPTW)是當前物流領域研究的熱點和難點。廣泛學者主要圍繞著該問題模型完善和求解算法改進進行了深入研究。如關于擁堵情形下的城市配送和互聯網租車等一系列VRPTW模型的構建[2,3]，以及多agent蟻群算法，改進蝙蝠算法，改進遺傳算法等VRPTW求解算法的設計[4-6]。但針對高原山地維修器材配送問題的VRPTW模型和算法成果較少。

針對上述問題，本文在前人研究的基礎上[7]，提出了高原山地“車輛+無人機”這一半無人化配送模式，構建了對應的VPRTW模型，并根據問題特征應用CTDEA算法對該問題進行了求解。

1 “車輛+無人機”配送模式

車輛配送是指對一系列卸(裝)貨點，組織適當的行車線路，在一定約束條件下(如貨物需求量、發貨量、交貨時間窗，車輛容量限制、時間限制等)的情況下，使車輛有序通過它們，以達到一定的目標(如距離最短，成本最低，時間最短等)。其特點是規模經濟性，但其單位配送成本高，載貨量較大，行駛范圍較廣但是受地形影響大[8,9]，如圖1。

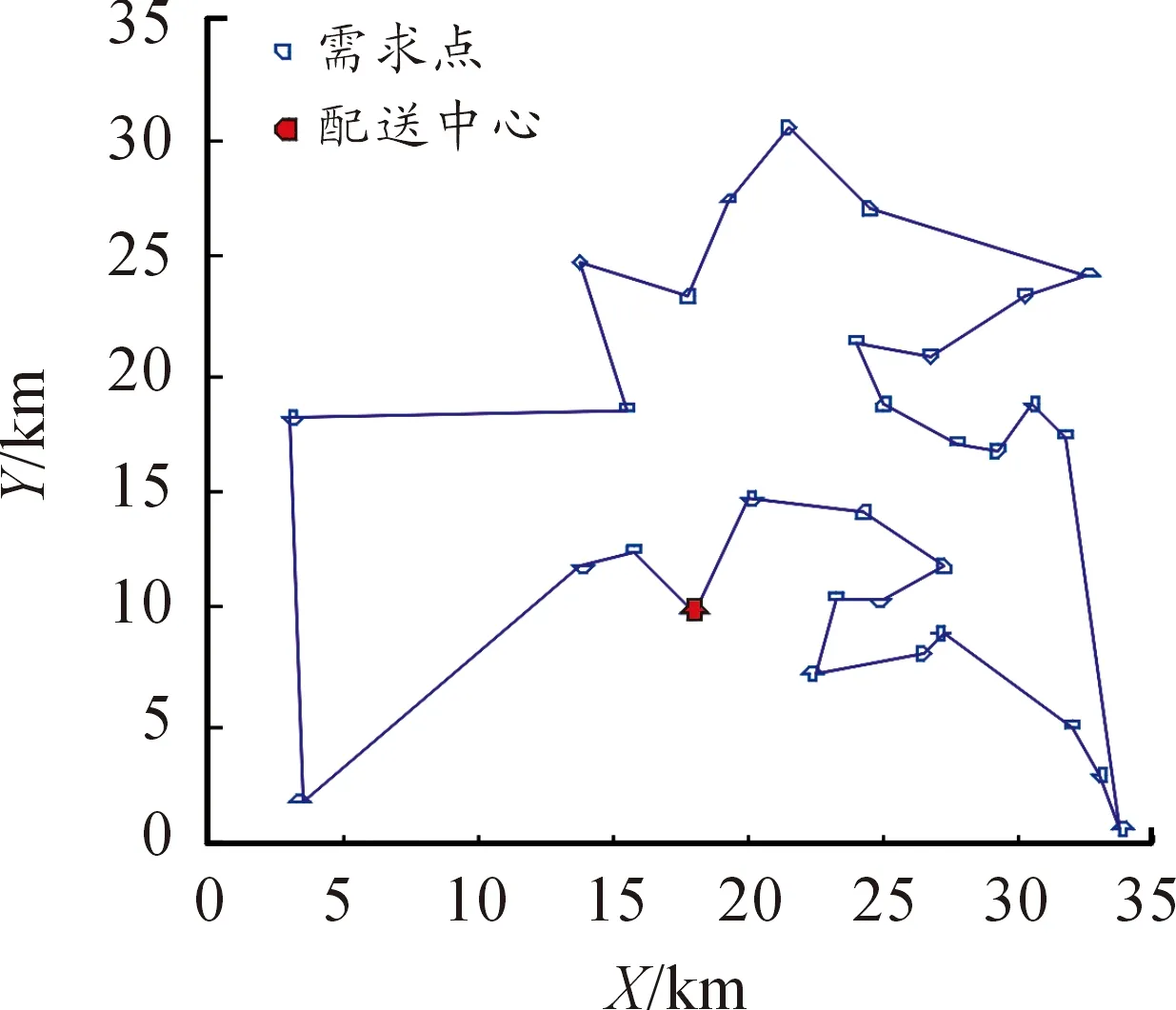
圖1 車輛配送模式下的路徑規劃示意圖

無人機是(Unmanned Aerial Vehicle，UAV)一種無需人員駕駛的空中飛行器，其利用內部配置的無線電遙控設備和預先編制好地控制程序實現自主飛行、獨立完成作戰或保障任務[10]。UAV具有機動靈活，隱蔽高效，安全經濟，受天氣、地形、道路交通影響小(見圖2)[11]，但載重量有限，飛行半徑較小的特點，見表1所示。

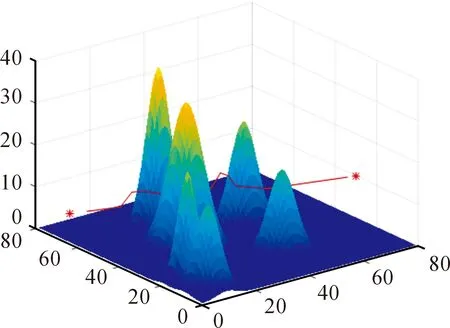
圖2 車輛不可通行地域的UAV配送示意圖

表1 UAV特點性能

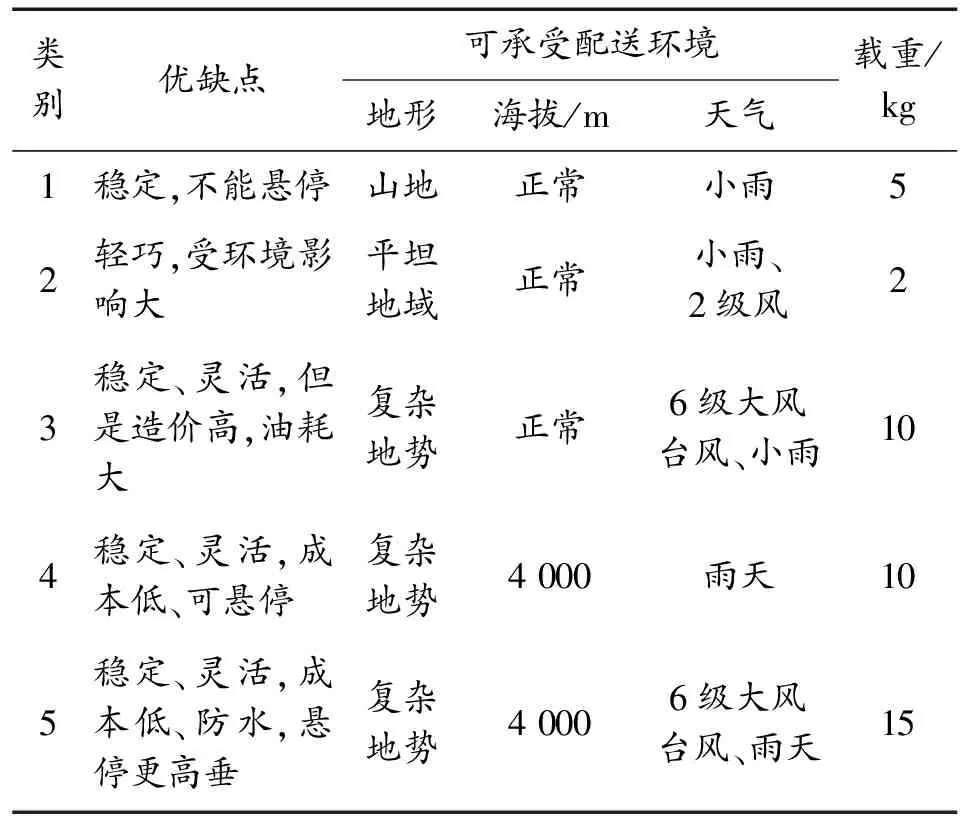
類別優缺點可承受配送環境地形海拔/m天氣載重/kg1穩定,不能懸停山地正常小雨52輕巧,受環境影響大平坦地域正常小雨、2級風23穩定、靈活,但是造價高,油耗大復雜地勢正常6級大風臺風、小雨104穩定、靈活,成本低、可懸停復雜地勢4 000雨天105穩定、靈活,成本低、防水,懸停更高垂復雜地勢4 0006級大風臺風、雨天15

注意：1為固定翼UAV，2為無尾翼UAV,3為無人直升機,4為四旋翼UAV,5為六旋翼UAV。

UAV配送模式在軍用和民用領域取得了長足發展。早在阿富汗戰爭，美軍無人運輸機K-MAX就出色完成了從后勤基地到偏遠山區前線陣地的配送任務，標志著UAV以“空中挑夫”身份正式出現在戰時配送領域。當前，軍用UAV配送了切合未來戰爭的信息化、網絡化、無人化的需求。在民用領域，UAV配送技術迅速風靡國內外。在國外，Reykjavik實現UAV送貨上門；ZIPLINE公司實現UAV以高達100 km/h的時速向診所運送血液。在國內，順豐建立了大型物流UAV基地，并提出“大型有人運輸機+支線大型UAV+末端小型UAV”的三段式空運網實現36 h通達全國的設想；京東研發出了能夠全自動化配送貨的六旋翼UAV；餓了么，美團外賣獲準開辟UAV即時配送航線，實現了UAV外賣配送的合法化,大幅提高了配送效率。

高原山地維修器材需求呈群落分布，群內需求量小、時效性強、位置分散且多位于車輛不可通行地域。傳統“車輛+人力”配送模式效率不高的問題亟待解決。當前UAV性能已可以勝任惡劣天氣下的高原山地配送任務(見表1)。車輛與UAV配送特點如表2，本研究通過UAV與車輛的優勢互補，用UAV取代傳統人力搬運作為直達作戰單元的配送方式，提出了一種“車輛+UAV”的高原山地維修器材配送模式。

表2 車輛與UAV配送特點

該模式的具體配送過程如下：配送中心對所獲取的作戰單元的需求利用諸如細菌搜索算法(Bacterial Foraging Algorithm,BFA)、K-means等聚類算法，對需求進行預處理，然后通過任務匹配確定執行任務的倉庫。按照車輛通行良好地域由車輛進行配送，車輛通行受限地域由車載UAV進行配送的原則，進行配送路徑規劃以實現總配送時間最短，如圖3所示。

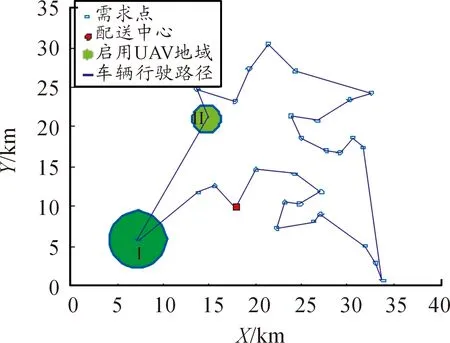
圖3 車輛+UAV配送路徑宏觀示意圖

“車輛+UAV”配送模式在配送過程中3種運動形式：① 同時啟用車輛和無人機均處于動態配送；② 受通行范圍限制，車輛在某一集散點等待，啟用無人機赴附近作戰單元進行配送，配送完后返回車輛所在位置；③ 車輛通行條件良好，啟用車輛配送，無人機暫不啟用。如圖4所示，此處考慮高原山地配送實務的特點，對如圖4(b)所示的情形進行研究。

2 車輛+UAV配送模式的模型設計

本文研究圖4(b)下的“車輛+UAV”路徑問題，可以看成嵌套的兩級帶時間窗的車輛路徑規劃(Vehicle Routing Problem with Time Windows,VRPTW)問題，車輛路徑規劃為Ι級VRPTW問題，UAV配送為ΙΙ級(即Ι級問題的子級問題)VRPTW問題。建模思路為，首先按車輛通行情況和距離對提出維修器材需求的作戰單元進行聚類分析，處理為作戰單元需求群，將每個需求群組視為1個Ι級需求點對車輛路徑進行優化。車輛通行受限的需求點，由車輛進行配送，車輛通行范圍受限需求群組啟用車輛+UAV配送模式，由車輛行駛至集散點，由無人機進行配送，其實質為一個局部VRPTW問題。故，車輛與UAV均遵循以下模型。

圖4 車輛+UAV配送路徑局部示意圖

2.1 符號說明

f(x):軍事效能；E：軍事效益

C1：電耗成本；C2：時間成本；C3：懲罰成本

w1w1,w2,w31：C1,C2,C3所對應的權重

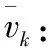
θ1：運輸工具空載時單位距離耗油/電成本

θ2：運輸工具滿載時單位距離耗油/電成本

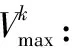
qg：需求點的需求量

cfk：每動用每一運輸工具的固定成本

Rk：所啟用的每一運輸工具數量

[ETi,LTi]：作戰單元的時間窗

M1(ti)：早到的懲罰成本函數

M2(ti)：[ETi,LTi]內到的懲罰成本函數

M3(ti)：晚到的懲罰成本函數

Vj：需求器材的容積；bj：需求器材的尺寸

2.2 模型構建

(1)

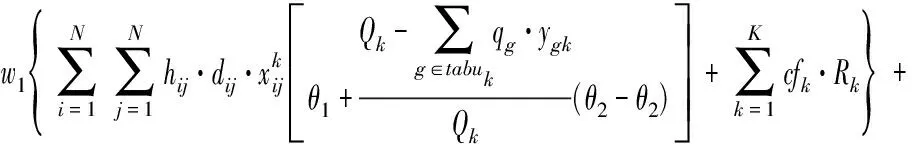
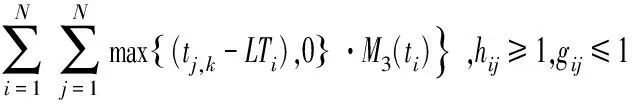
(2)

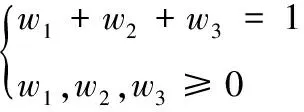
(3)

(4)

(5)

(6)

(7)

(8)

(9)

twait,i,k=max(ETi,k-ti,k,0)

(10)

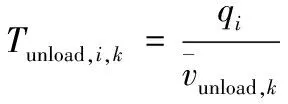
(11)

tj,k=ti,k+twait,i,k+Tunload,i,k+tij,i,k

(12)

(13)

(14)

(15)

根據高原山地軍用維修器材配送任務的特點，本研究將軍事效能最大化作為目標函數，見式(1)。由于指定配送任務對應的軍事效益E為定值，所以上述目標即可轉化為油/電耗成本、時間成本和懲罰成本最小化，見式(2)。結合高原山地配送中道路彎多坡陡，車輛故障高發，車速受路況影響較大，且油耗成本大的實際，引入了距離修正因子hij和速度修正因子gij和基于車輛實載率核算的單位油耗成本(對于不受上述因素影響的UAV，其對應參數hij,gij可取1)。上述模型中的hij,gij可由信息平臺根據所獲取各節點間路段i→j的實時道路信息進行賦值，θ1,θ2根據信息平臺記錄的車輛油耗歷史數據得到。由于實際情況下作戰單元的時間窗為無時間窗、軟時間窗、硬時間窗、混合時間窗共存，故本文通過設置不同時段的懲罰函數來描繪不同時間窗下的懲罰成本。其中，無時間窗情況下，M(ti)均取0；硬時間窗下，令M1(ti),M3(ti)→∞，M2(ti)取1；軟時間窗和混時間窗下根據作戰單元需求規律設置懲罰函數表達式。式(3)表示多目標處理為單一目標函數時各子目標的權重約束。由于維修器材裝載不同傳統物資裝載，所以其裝載除了車輛載荷和容量約束外，還要考慮裝貨尺寸的約束，見式(4)～式(6)。式(7)～式(9)分別表示每個作戰單元最多有且只有一輛運輸工具為其服務;運輸工具訪問每個節點后必須從該節點駛離，然后進行下一個作戰單元的配送或返回配送中轉點(起始點)；運輸工具必須從起始點出發最終返回起始點，并且運輸工具數量不能超過可用運輸工具總數K。式(10)～式(12)分別表示在作戰單元處i的等待時間，卸貨時間和到達作戰單元處j的時間，其中卸貨時間由器材卸貨量和器材的卸貨速度決定。式(13)～式(15)均為0-1決策變量。

3 求解算法

無人機配送路徑規劃問題的實質仍為VRPTW問題，二者均屬于NP-hard問題，一般采用啟發式算法來進行求解。以GA算法為代表的進化算法因具有較高的魯棒性、高效率和廣泛適用性的全局優化特點，被廣泛用于上述大規模復雜組合優化的求解。但是傳統演化算法普遍存在由于種群多樣性下降而導致過早收斂，陷入局部最優的局限。針對這一問題，譚陽等[12]提出了基于染色體異位的動態進化算法(Chromosomal Translocation-based Dynamic Evolutionary Algorithm,CTDEA)，該算法在維護種群多樣性、求解速度、解的精度、和穩定性上較遺傳算法(GA)均由明顯改進。故此處選取該算法對上述VRPTW+UAVRPTW問題進行求解。

3.1 算法步驟

步驟1 初始化種群P0;

步驟2 互斥操作：對Pt進行互斥操作(去除差個體i,j間差異度d(ai,aj)相同的個體)并根據目標適應度Fit(f(ai))按降序排列。

(16)

其中，Div(ai)為個體在種群中的差異度。

步驟3 判斷是否滿足終止條件，滿足即跳出循環，否則繼續執行步驟4。

步驟4 精英策略：篩選Fit(f(ai))排序為前m的個體構成精英群，并計算Div(ai)

步驟5 交叉操作：其余n-m個體，根據式(17)在步驟4的精英群中選擇一個精英個體，按式(18)進行交叉操作

(17)

(18)

其中，ai,l表示個體ai在其種群中的第l個編碼位。

步驟6 多樣性度量。計算當前基因矩陣所有列的多樣性度量Div(j)，將結果按降序排列存入Div_column，按式(19)求基因矩陣多樣性度量Div(At)；

(19)

其中，Div(At)=0,1,2,…,n×L,且其值越逼近0，種群多樣性越高。

步驟7 易位操作：根據式(20)對比多樣性Div(At)，根據K值，按式(21)對Div_column中的前K列進行反置易位操作，之后執行步驟2。

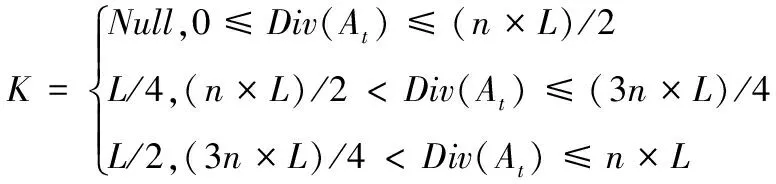
(20)

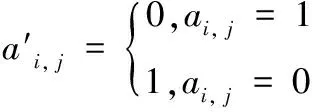
(21)

3.2 算法流程

CTDEA算法流程如圖5所示。

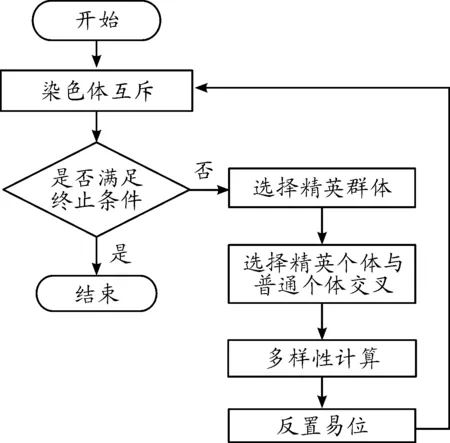
圖5 CTDEA算法流程框圖

4 算例分析

4.1 背景案例

假設配送中心收到高原山地作戰單元維修器材需求信息見表3。

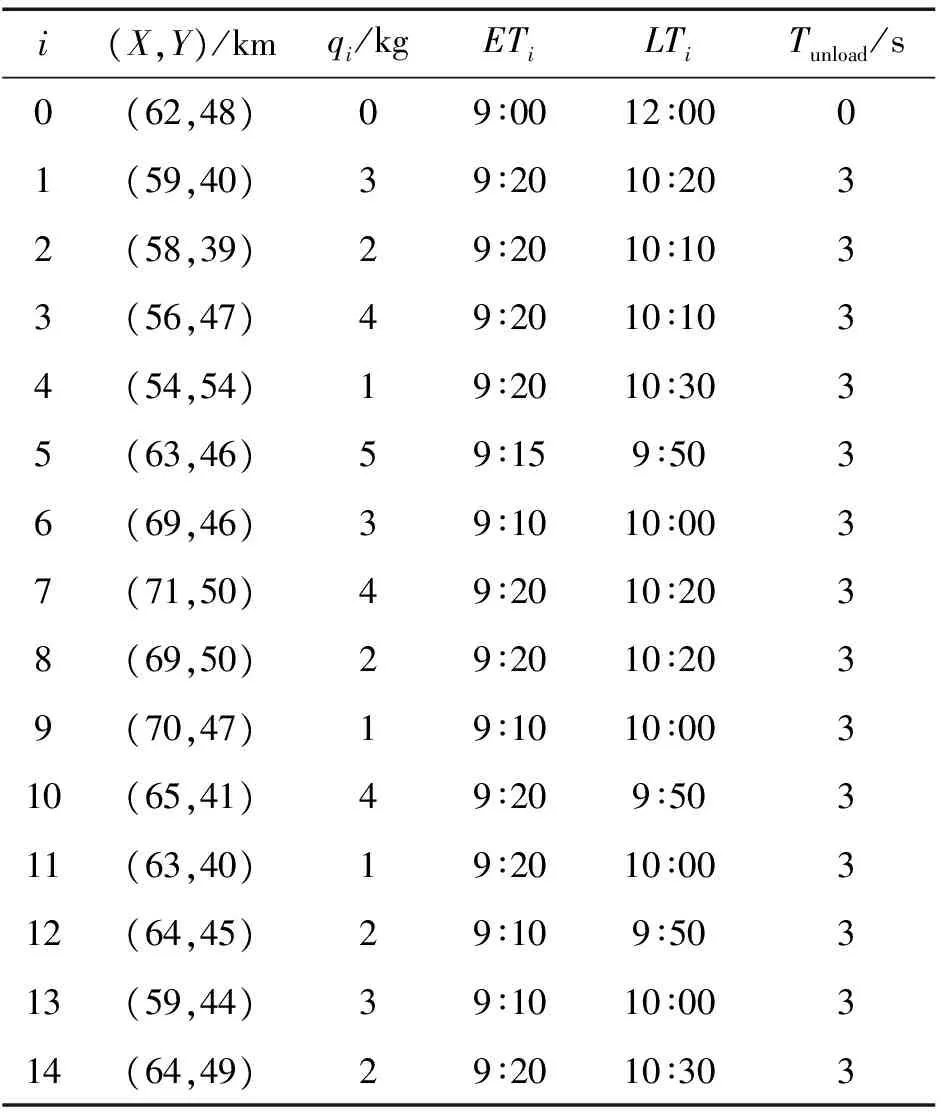
表3 作戰單元需求信息

經過任務匹配，倉庫A負責此次配送任務。考慮由于該次配送任務所屬地域地形復雜，車輛通行范圍受限，故調用車輛+六旋翼UVA執行此次任務,該UAV性能見表1，飛行半徑20 km，平均航行速度為15 m/s。配送流程為車輛裝載UVA直達中轉集散點0，然后啟用UAV進行“最后一公里”末端配送。車輛至0的路程為20 km,平均車速為60 km/h，最載重1.6 t，該車隊于9點從A出發。要求對UAV配送路徑進行規劃，使得在動用UAV架次最少的基礎上實現配送時間最短。

4.2 CTDEA算法和GA算法運行結果

由于車輛均是從A到0，距離均為20 km，用時20 min,抵達中轉點0的時刻為9∶20≤ETi,故該背景案例中的VRPTW+UAVRPTW問題，僅需要對UAVRPTW進行處理即可。利用CTDEA算法和GA算法同時求解，Matlab的運行結果如表4、表5所示。

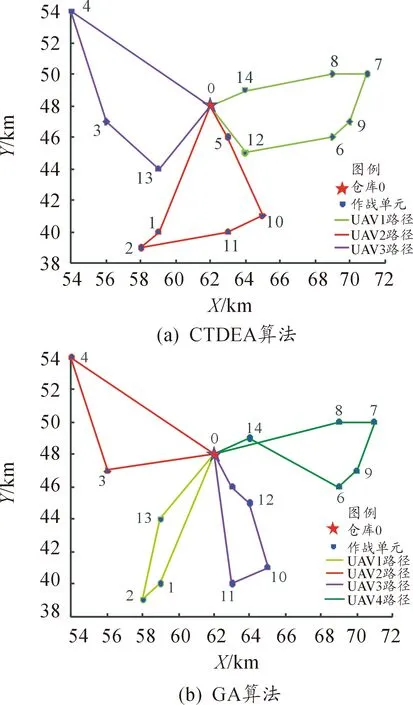
圖6 CTDEA算法和GA算法下的UAV配送路徑圖

表4 CTDEA算法求解結果

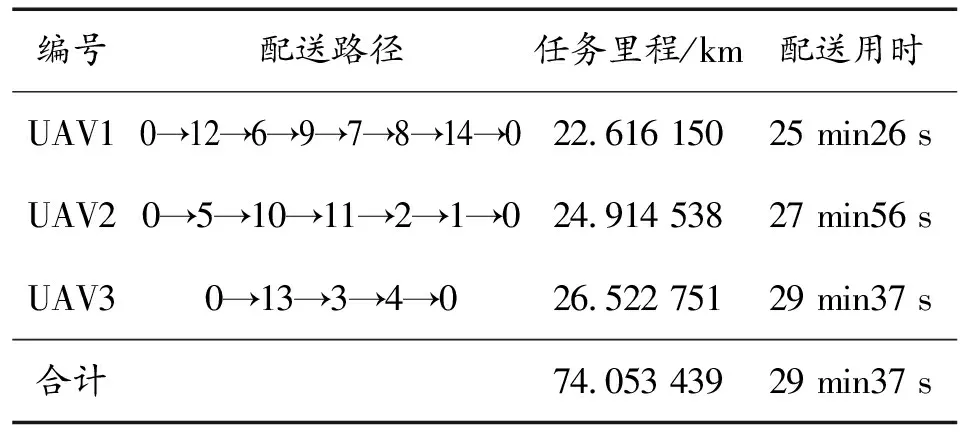
編號配送路徑任務里程/km配送用時UAV10→12→6→9→7→8→14→022.616 15025 min26 sUAV20→5→10→11→2→1→024.914 53827 min56 sUAV30→13→3→4→026.522 75129 min37 s合計74.053 43929 min37 s

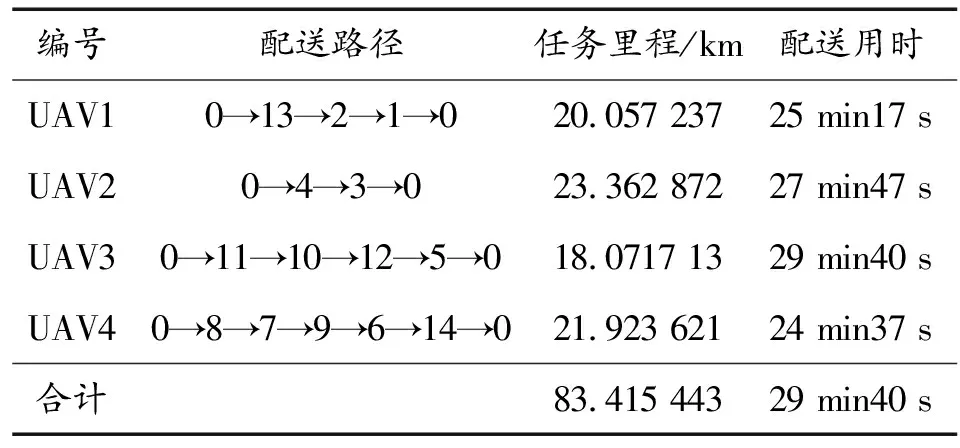
表5 GA算法求解結果

如表4、表5所示，CTDEA算法求解結果為UAV動用架次為3，總任務里程為74.053 4 km，由于UAV并行執行任務，總任務耗時29 min37 s，GA算法求解結果為UAV動用架次為4，總任務里程為83.415 4 km，總任務耗時29 min40 s,如圖6所示。

通過對高原山地維修器材配送實際的背景案例的仿真分析，發現CTDEA算法在求解質量和收斂代數方面均好于GA算法(見圖7)，有效解決了傳統進化算法因種群多樣性下降導致早熟問題。其中，GA算法在進入較少代數后由于受目標函數極小值吸引速喪失種群多樣性，陷入局部最優，全局搜索能力較差。相比于GA算法，CTDEA算法能夠通過染色體異位保障了種群多樣性，從而使得算法可以跳出陷入局部最優的困境，避免算法過早進入早熟，提高了算法的全局搜索能力和求解質量；同時從收斂代數上來看，CTDEA算法具有較好局部尋優能力和收斂速度。

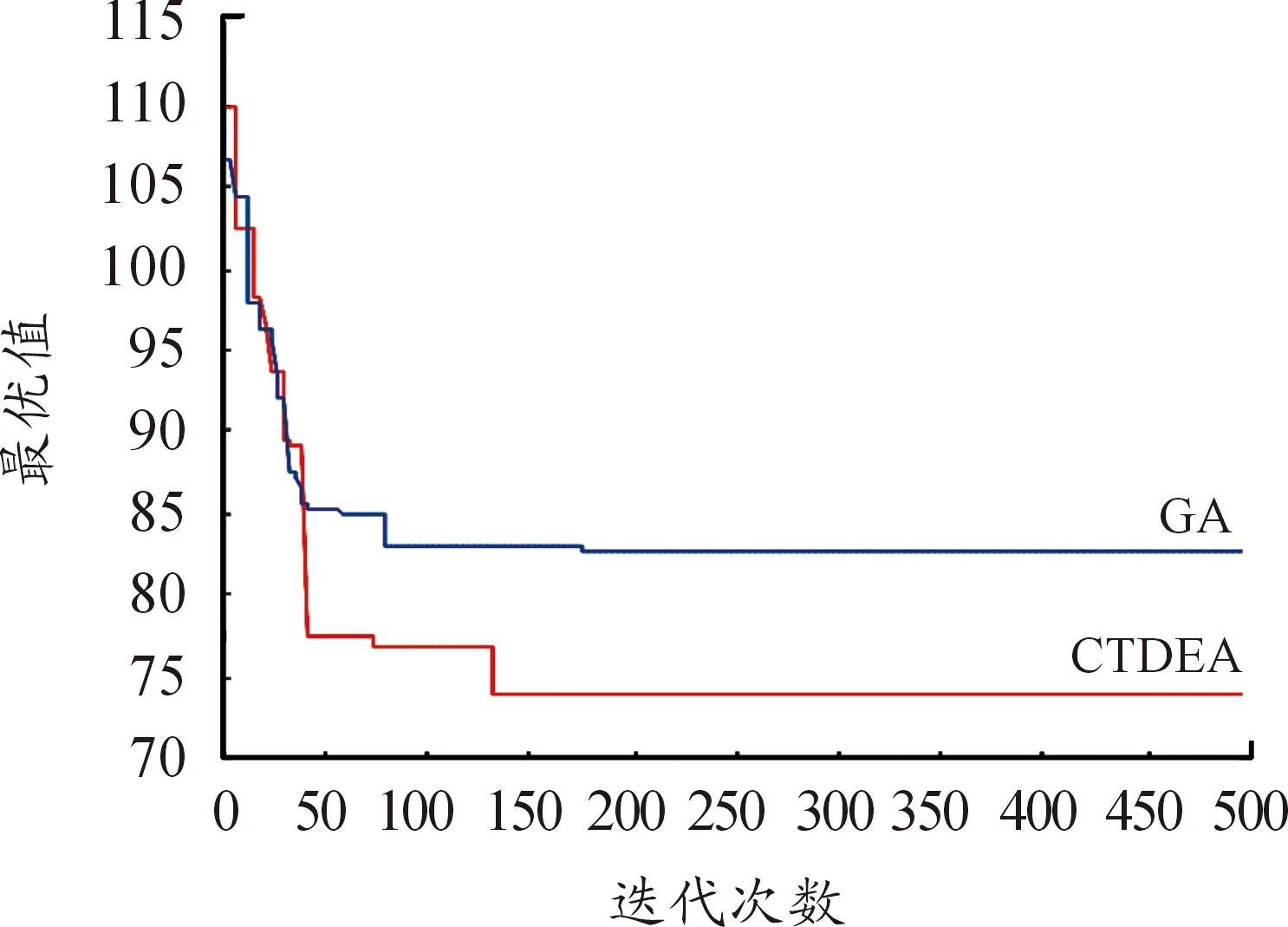
圖7 CTDEA算法與GA算法下迭代次數與最優值關系

4.3 “車輛+UAV”和“車輛+人力搬運”

根據高原山地單兵負重研究，海拔3 700 m人力搬運速度為4 km/h,4.5 km/h,5 km/h分別對應基準適宜負重為20.5 kg,18.0 kg,15.0 kg。鑒于配送任務的時效性，選取5 km/h,15.0 kg這一數組用于對比，Tunload取1 min/單元。通過求解，得該模式需3名單兵，總里程74.053 4 km，合計用時5 h21 min,配送效率為“車輛+UAV”的1/10.84，且難以滿足時間窗需求。

5 結論

本文提出了一種“車輛+UAV”的半自主配送模式。通過仿真實驗驗證了“車輛+UAV”配送方式較傳統配送方式在配送效率和時效性方面的優越性以及CTDEA算法的有效性。