一種新型發動機功率試飛數據處理和代理模型建模方法
周靈玲,邱良軍
(中國直升機設計研究所,江西 景德鎮 333001)
0 引言
計算直升機的基本飛行性能主要是確定直升機的飛行需用功率和發動機可用功率,當兩者相等時就可得到相應狀態的基本飛行性能。因此,準確計算發動機可用功率是正確分析直升機基本飛行性能的前提。傳統的發動機可用功率處理方法主要采用發動機參數換算和基于百分比的安裝損失扣除,無法考慮現代渦輪軸發動機性能曲線的非線性變化,與實測發動機性能曲線特點有所差別。本文提出一種新的發動機功率試飛數據處理方法,并建立發動機可用功率代理模型。通過直升機實際試飛驗證,新的發動機功率試飛數據處理方法相比傳統的發動機可用功率處理方法,可以考慮發動機性能曲線的非線性變化;運用建立的發動機可用功率代理模型,不僅可以提高發動機功率數據處理和計算的精度,同時還可以考慮發動機安裝損失和實際試飛中所需留取的余量。此外,可以使用海平面的發動機試驗數據推算發動機安裝損失和高原發動機功率,有效提高了高原基本飛行性能的計算精度。
1 傳統發動機功率分析方法的弊端
發動機的主要性能參數包括動力渦輪前溫度ITT、壓氣機轉速Ng和輸出功率Pw,通過給定ITT和Ng閾值限制發動機的工作狀態。根據理想循環的發動機模型可以推導得到如下的發動機性能參數換算公式(1)-(3),其中ITTN為換算動力渦輪前溫度,NgN為換算壓氣機轉速,PwN為換算輸出功率,θ為溫度比,Δ為壓力比[1]。
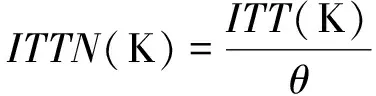
(1)
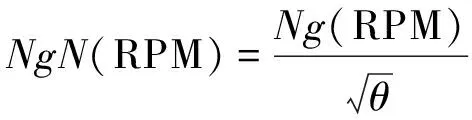
(2)
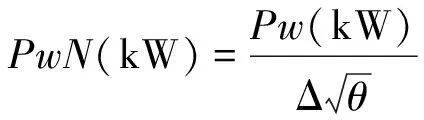
(3)
傳統發動機可用功率處理方法主要通過將不同高度的發動機性能數據點換算后進行數據擬合,獲得發動機的性能曲線,再進行反向換算得到所需壓力高度和大氣溫度的發動機性能,然后通過固定的百分比扣除發動機安裝損失和功率修正,最終得到發動機可用功率。
對于典型現代民用直升機,平飛狀態占其總使用時間超過55%,大部分時間發動機工作在低于最大連續功率的巡航功率狀態。以加拿大普惠公司的PT6B發動機(應用于AC313直升機)和法國透博梅卡的Arrius2K2發動機(應用于3噸機)為代表的現代渦輪軸發動機針對這一使用特點,在壓氣機和燃燒室之間采用放氣活門設計,以調節進入發動機后段(包括燃燒室和動力渦輪等)的氣流流量,減小壓氣機能力需求,提高其功重比和經濟性[2]。其典型發動機性能曲線如圖1所示。在最大連續功率之前的A段,放氣活門打開,放走多余氣流,保證發動機后段處于效率最高的狀態,降低巡航狀態的發動機油耗。在最大連續功率之后的B段,放氣活門關閉,壓氣機全力工作以獲得更高的起飛功率和應急功率,但是壓氣機流量仍小于發動機后段所需的最佳流量,燃燒室和渦輪工作效率下降,輸出功率隨渦輪前溫度增長的速度相比A段減小。
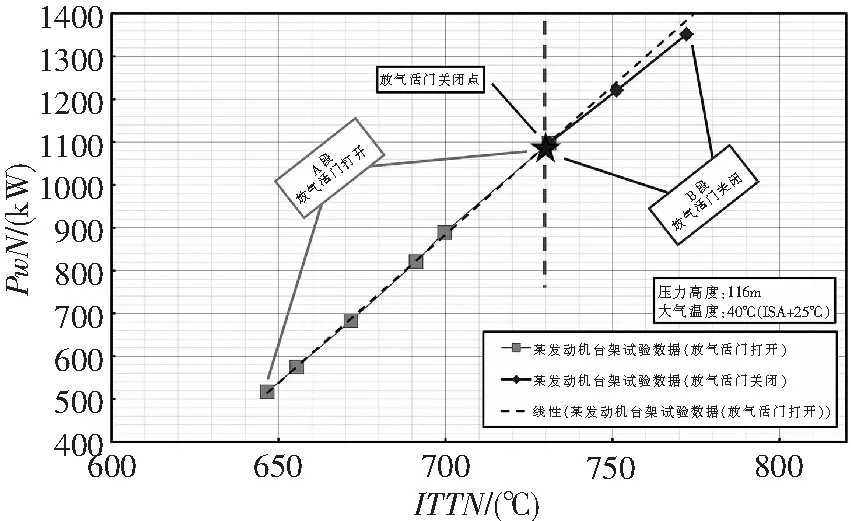
圖1 某現代渦軸發動機放氣活門打開和關閉的
因此,現代渦輪軸發動機的性能曲線通常分為兩段,存在兩個不同斜率,中間出現拐點,即放氣活門關閉點。該放氣活門關閉點設計在最大連續功率之前,以提高燃燒室和渦輪效率,降低巡航狀態的發動機油耗,并以此點優化壓氣機設計,減小發動機重量,相比以往根據最大功率設計的老式渦輪軸發動機,可以提高發動機的功重比和經濟性。
使用傳統換算方法處理此類現代渦輪軸發動機數據,設發動機功率隨渦輪前溫度ITT增大為線性關系,則可設放氣活門打開狀態下的發動機輸出功率和放氣活門關閉狀態下的發動機輸出功率為下式(4)和(5)。其中,放氣活門關閉前后的截距b開≠b閉,斜率k開≠k閉。
Pw開=k開ITT+b開
(4)
Pw閉=k閉ITT+b閉
(5)
根據(1)和(3)式,可推導得換算功率為:

(6)

(7)
則可以得到如下關系式(8)和(9),表明放氣活門關閉前后的發動機性能換算曲線不相等,前述通過換算處理發動機功率的傳統方法僅適用于性能曲線線性一致的老式渦輪軸發動機。對于現代渦輪軸發動機,雖然海平面下放氣活門關閉前后斜率和截距差別相對較小,但是對比后續第2節的算例,高原條件下的放氣活門關閉前斜率比關閉后大30%,截距相差40%,強行使用換算方法處理將引入較大的方法誤差。
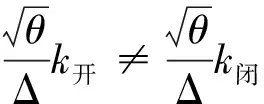
(8)
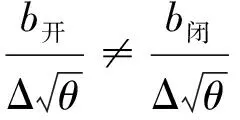
(9)
此外,發動機性能曲線的斜率k和截距b是隨壓力高度和溫度變化的,傳統換算方法同樣無法考慮由于大氣環境導致的發動機換算性能曲線的非線性變化。
因此,理論分析和型號實踐都表明使用該方法處理現代渦輪軸發動機數據將帶來顯著誤差,無法滿足工程精度要求。
2 發動機性能曲線建模
根據第一節的分析,現代渦輪軸發動機的性能曲線可以抽象成兩段相交直線或者二階多項式的幾何模型。根據這個特點可以建立發動機試飛數據的處理方法,并建立發動機功率代理模型,其具體求解流程如下:
1)根據發動機廠商提供的放氣活門參考關閉點,對給定壓力高度和溫度的發動機數據進行分類,區分放氣活門關閉前的和關閉后的數據;
2)通過對放氣活門關閉點前后的發動機數據分別進行最小二乘法擬合,確定兩段直線的截距b閉、b開與斜率k閉、k開,或者二階多項式系數。設現有n個相同放氣活門狀態的數據點,對于第i個數據點,其渦輪前溫度為ITTi,壓氣機轉速為Ngi,輸出功率為Pwi,如使用最小二乘法進行線性回歸,可建立數據矩陣AITT與BPw,待求系數矩陣xITT,定義如下:
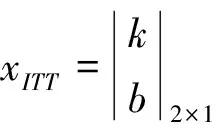
(10)
如使用最小二乘法進行二階多項式回歸,則可建立數據矩陣AITT與BPw,待求系數矩陣xITT,定義如下:
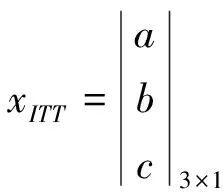
(11)
使用QR分解和最小二乘法求解AITTxITT=BPw,可得渦輪前溫度ITT的系數矩陣xITT,確定兩段直線的截距b閉、b開與斜率k閉、k開,或者二階多項式系數。相似方法可算得壓氣機轉速Ng的系數矩陣xNg及其系數;
3)根據發動機廠商提供的發動機功率狀態設定ITT和Ng參數限制;
4)由發動機功率狀態對應的參數限制求得對應的發動機功率Pw。對于考慮實際飛行操作中給飛行員留予一定的余量的問題,也可以通過直接給定ITT和Ng,求得對應發動機功率Pw;
5)對各個高度和溫度組合完成1)到3)的步驟,得到系數矩陣。對于給定的壓力高度和溫度,通過對數據矩陣進行二維插值得到相應的直線的截距b閉、b開與斜率k閉、k開,或者二階多項式系數,進而算得發動機功率,從而建立發動機輸出功率代理模型。
圖2為某現代渦軸發動機高原無地效懸停實測數據算例,可以看出性能曲線拐點前后的曲線斜率和截距有明顯差別。使用本文方法可以算得截距b閉=-2890.1和b開=-5059.3,斜率k閉=5.2441和k開=7.9604,對應發動機功率的ITT限制,最大連續功率的PwN為1410kW,最大起飛功率的PwN為1619kW。
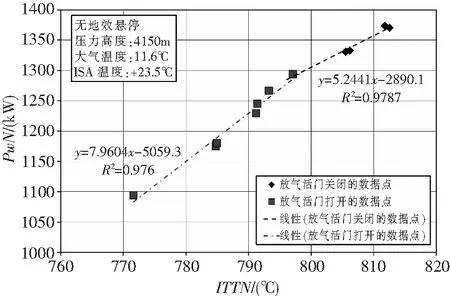
圖2 某現代渦軸發動機高原無地效懸停實測數據算例
3 發動機安裝損失的扣除
傳統發動機可用功率處理方法是直接給定各功率狀態臺架功率,再按固定百分比扣除發動機安裝損失后得到發動機的可用功率,如下式所示,其中δ為固定的安裝損失百分比,發動機安裝損失功率隨發動機功率增大而增大。
Pw安裝后=Pw臺架(1-δ)
(12)
圖3為無地效懸停時的典型發動機性能實測數據與臺架性能曲線對比,兩者之間的差異就是發動機的安裝損失。可以看出實測性能曲線與臺架性能曲線之間不是固定百分比的關系,而是近似平行偏移的關系,發動機的安裝損失功率近似為一個常數,發動機安裝損失功率隨發動機功率增大而保持不變或者略微減小,與傳統按固定百分比扣除的方法的損失變化特性相反。傳統方法將高估大功率狀態下的安裝損失,特別是對于主要對應于大功率狀態的基本飛行性能分析,將導致性能損失。此外,傳統直接給定各功率狀態臺架功率的方法也難以根據平行偏移關系計算可用功率。因此,需要使用第2節的方法建立發動機臺架性能曲線模型,根據實測數據與發動機基準性能曲線對比獲得性能曲線平行偏移量,對發動機臺架性能曲線模型進行平行偏移后得到扣除安裝損失后的發動機性能曲線。設發動機臺架功率為ITT的函數,記為Pw臺架(ITT),則扣除發動機安裝損失后得到發動機的可用功率函數Pw安裝后為:
Pw安裝后(ITT)=Pw臺架(ITT-ITT偏移量)
(13)
其中ITT偏移量為相同輸出功率下,臺架性能曲線的對應ITT與實測性能曲線對應ITT之差。
圖4為發動機在不同壓力高度無地效懸停實測性能曲線ITT偏移量對比。
由圖4可以看出海平面的平行偏移量和高原的平行偏移量大致相當。在只有海平面試驗數據時,可以使用海平面的發動機試驗數據推算ITTN平均偏移量,進而獲得高原發動機可用功率,有效提高高原基本飛行性能的計算精度。在獲得高原試飛數據后,可以對ITTN偏移量進行線性擬合,從而進一步考慮發動機安裝損失隨壓力高度的變化。
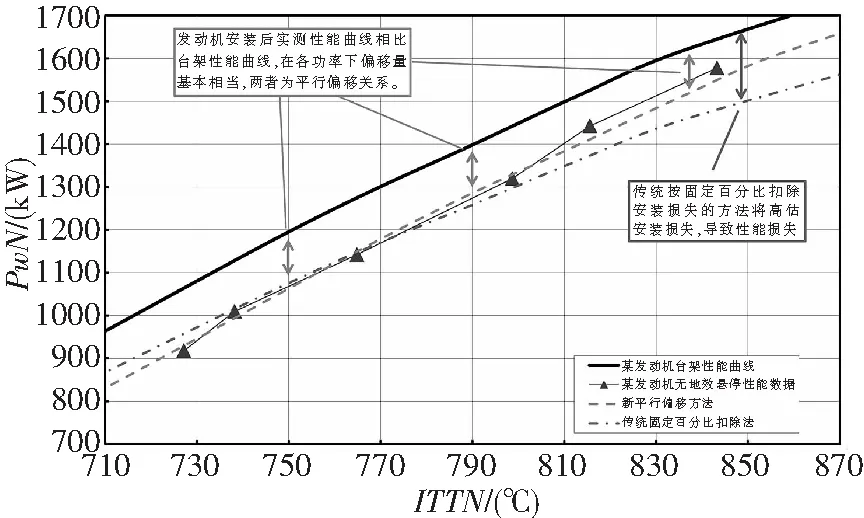
圖3 某現代渦軸發動機無地效懸停實測性能曲線和臺架性能曲線對比
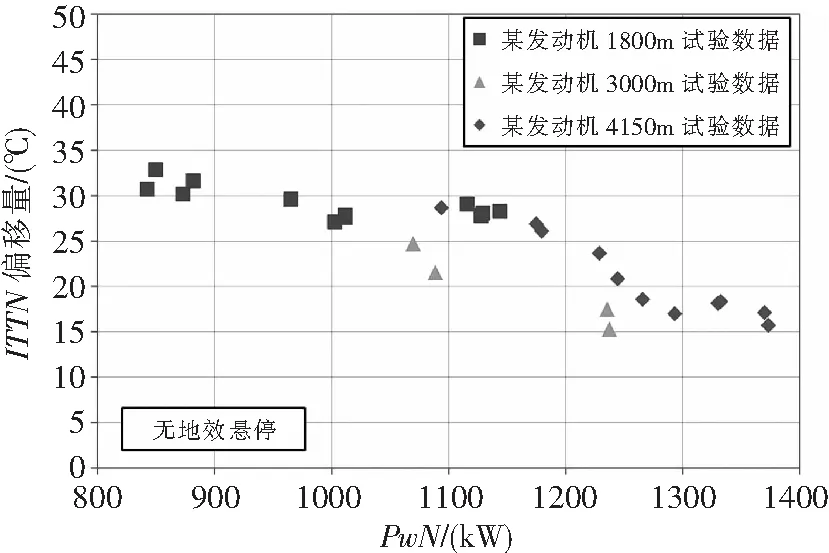
圖4 某現代渦軸發動機不同壓力高度無地效懸停實測性能ITT偏移量對比
4 計算結果與實測性能對比
圖5為新的發動機功率處理結果、傳統換算方法處理結果以及實測數據對比圖。
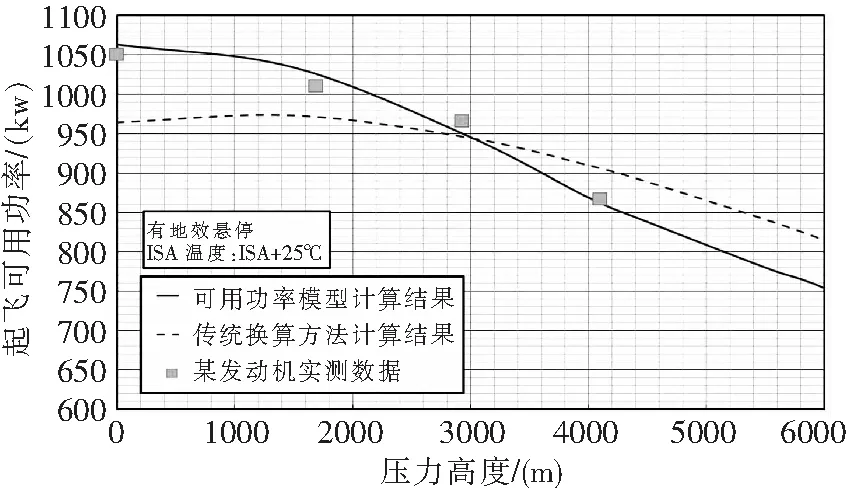
圖5 新的發動機功率模型起飛功率計算結果和傳統換算方法計算結果對比圖
可以看出,傳統方法在低高度的計算結果,發動機功率隨高度減小反而減小,計算結果不合理。新的發動機可用功率處理方法相比傳統方法能夠更準確地描述發動機可用功率隨壓力高度的變化,處理結果更加準確有效。
5 結論
本文提出一種新的發動機功率試飛數據處理方法,并建立發動機可用功率代理模型。型號驗證表明,該方法相比傳統分析方法主要有如下優點:
1)可以考慮發動機性能曲線的非線性變化,顯著提高發動機可用功率計算精度,計算結果的性能曲線趨勢合理;
2)發動機安裝損失處理方法與實測損失特性相符,可以使用海平面的發動機試驗數據推算安裝損失和高原發動機可用功率,有效提高高原試飛數據處理精度和高原基本飛行性能的計算精度;
3)可以更簡便地考慮實際試飛中所需留取的余量,方便試飛任務仿真計算。

