渤海油田油氣井套管腐蝕及磨損數值模擬研究

元少平，羅 衡，蔡 鵬，毛 煉，劉興華

(中海油安全技術服務有限公司 天津300456)

0 引 言

井完整性是保障油氣田安全生產的關鍵。但隨著生產年限的增加，越來越多的油套管不可避免地會發生各式各樣的損壞。石油套管在井下不僅與腐蝕性介質直接接觸，同時還承受拉伸、彎曲、擠壓等復雜應力的作用，苛刻的工作環境直接影響其壽命長短[1-2]。實際作業中套管失效的形式一般包括套管錯斷、套管裂開、套管徑向變形或擠毀套管剪斷、套管屈曲失穩、腐蝕和磨損等形式。

國內外研究者針對套管強度設計開展了相關研究。李斌等[3]考慮材料非線性的基礎上，利用數值軟件，分析了磨損套管在均勻外壓和非均勻外壓下的抗擠強度；覃成錦等、高智海等[4-5]采用有限元法完成了不同受荷形式下的套管抗擠強度計算和規律性研究；法國學者 Levy[6]建立了標準圓柱形管柱外壓彈性擠毀公式，成為美國石油學會制定套管擠毀計算的理論基礎；Clinedinst[7]研究了沿套管壁厚呈線性和雙曲壓力作用下，套管臨界擠毀壓力；Mimura等[8]推導了套管壁厚變化對擠毀壓力的計算公式；Song等[9]采用解析法和Mises理論討論了月牙形磨損套管破裂強度；Huang等[10]將套管外壁屈服強度作為套管失效的標準，建立了二維彈塑性有限元模型，計算了偏心磨損對套管強度的影響。基于上述分析，從套管失效模式與機理研究入手，結合現場套管損傷情況，通過對測井數據計算分析獲得套管損傷位置、大小等具體信息，對套管進行損傷分類和定量化處理，進而建立套管剩余強度計算模型。

套管腐蝕：大多數氣井所處的井下環境十分惡劣，氣井壓力高，腐蝕性介質多、含量高，使井下的油套管發生嚴重的腐蝕破壞，氣井腐蝕主要是 H2S、CO2、Cl-1以及這 3種因素共同作用產生的結果。除此以外，在酸化作業中，由于排液不徹底，擠入深度地層酸沒有排出，隨著生產，氣流帶出沉入井底，井的下部含有大量沒有排出的殘酸，使井下部 pH值下降，氫離子濃度增加，從而使油管腐蝕加劇。

磨損：在深井和超深井鉆井過程中，套管磨損是一個日益突出的問題，由于深井和超深井在鉆進過程中需要穿過各種壓力和巖性不同的地層，導致井眼軌跡變化復雜，使鉆桿與套管間的摩擦不可避免地增加；同時由于鉆桿長度大、剛度小、撓度大等，使鉆桿在鉆進過程中運動情況變得復雜而與套管間發生接觸、磨損和刮傷，使得套管剩余強度降低。而套管不僅要保證鉆井作業的正常進行，還必須確保套管在鉆井完成后具有足夠的剩余強度以便能夠完成后續的固井、完井以及生產作業。因此，對磨損后套管應力的預測成為廣大鉆井工程技術人員關注的焦點，也已經成為鉆井過程急需解決的關鍵問題之一。

1 API套管強度計算

當外擠壓應力作用在套管管壁上使套管材料達到屈服強度時，管體將發生塑性變形，此時即被認為不安全。當管體發生塑性變形時，通過承受均勻載荷的厚壁筒的拉梅公式，同時根據已知數據，可推導出如下API屈服強度擠毀公式：

式中：Pco為抗擠強度，MPa；YP為套管材料最小屈服強度，YP＝551MPa；DC為套管外徑，DC＝244.5mm；δ為套管壁厚，δ＝12mm。

管體破裂壓力是指套管的最小內壓力達到管體鋼材屈服極限所需的壓力，API明確給出了套管管體抗內壓強度的計算公式，又稱Barlow公式。

根據剩余抗擠強度公式：

剩余抗壓強度公式：

式中：v—腐蝕速率，取v＝0.18mm/a。

根據套管理論實際受擠壓：

式(5)中 1.1MPa為考慮環空帶壓值，0.0098×1.2×3060為考慮靜液柱壓力值。

理論實際受內壓：

式中：0.925g/cm3為油密度；1.1MPa為井口壓力。

當剩余強度低于實際受壓時，套管失效；當腐蝕達到 20年時，剩余抗擠強度 Pco≈ 36.5MPa ，剩余抗壓強度 Pbo≈ 37.35MPa 。因為 Pco＜Pc，所以推導出該規格套管理論運行時效t≈19年。同時考慮到抗壓安全系數為1.1，所以安全運行時效t≈14年。

2 套管有限元模型

為得到不同深度點蝕坑對套管剩余強度的影響，點蝕深度按照腐蝕速率(0.18mm/a)分別取為 1年0.18mm，5年 0.9～1.2mm，10年 1.8～2mm，10年后2～3mm。

3 套管腐蝕剩余強度分析

3.1 套管初始受壓

根據式(1)所得套管擠毀強度可知，套管運行良好，考慮兩端固定約束故最大應力產生在兩端應力集中處，但套管內外主要受力面并未被擠毀或壓毀，同時推測應力集中區域容易發生腐蝕，所以將腐蝕坑設定在套管中心部位(圖1)。

3.2 考慮1年后點腐蝕(深度0.18 mm)

不考慮兩端應力集中，套管壁應力變化較小，內外壁受壓約為 26MPa，0.18mm 點腐蝕(初始為圓狀)周圍的應力約為 27MPa，對套管影響很小。點腐蝕坑存在應力集中，最大應力34MPa，推測腐蝕形狀沿兩端加深，會形成橢圓狀點蝕坑(圖2)。

圖1 初始套管應力分布Fig.1 Initial casing stress distribution

圖2 球狀腐蝕(0.18mm)Fig.2 Spherical corrosion shapes(0.18mm)

3.3 考慮1年后橢圓腐蝕(深度0.18 mm)

不考慮兩端應力集中，套管壁應力變化較小，內外壁受壓約為 27MPa，0.18mm 橢圓腐蝕周圍的應力也約為 27MPa。橢圓腐蝕坑存在應力集中，最大應力47MPa，橢圓點失效，并且周圍0.05mm深度區域也失效。但對套管的影響可忽略，套管依然能夠正常承載運行(圖3)。

圖3 橢圓狀腐蝕(0.18mm)Fig.3 Elliptic corrosion shapes(0.18mm)

3.4 考慮5年后雙圓點腐蝕(深度1 mm)

因為套管腐蝕缺陷的分布往往呈現出隨機性，有的部分以單腐蝕坑形式出現，有的部分是相鄰的多個腐蝕坑不規則分布，所以考慮了相鄰腐蝕坑對套管的應力分布影響(圖4)。根據剩余抗壓和抗擠強度公式可得，5年腐蝕深度約為 1mm 時，剩余抗內壓強度約為 49MPa，剩余抗擠強度約為 47.5MPa。所以從圖4可以得到，多坑腐蝕 5年后，套管中部深 1mm的部分區域開始屈服，雖然套管依然能夠正常運行，但應力集中處(螺紋連接區域)套管內部開始屈服。

3.5 考慮5年后雙橢圓點腐蝕(深度1 mm)

圖5展示的現象和圖4相似，因為腐蝕坑為橢圓，最大應力并未在腐蝕坑中出現，應力集中主要存在套管兩端，并且大于腐蝕坑為半球形時的套管受到的最大應力。所以從圖5可以得到，多橢圓坑腐蝕5年后，套管中部深 1mm 的部分區域開始屈服，但是套管依然能夠正常運行。

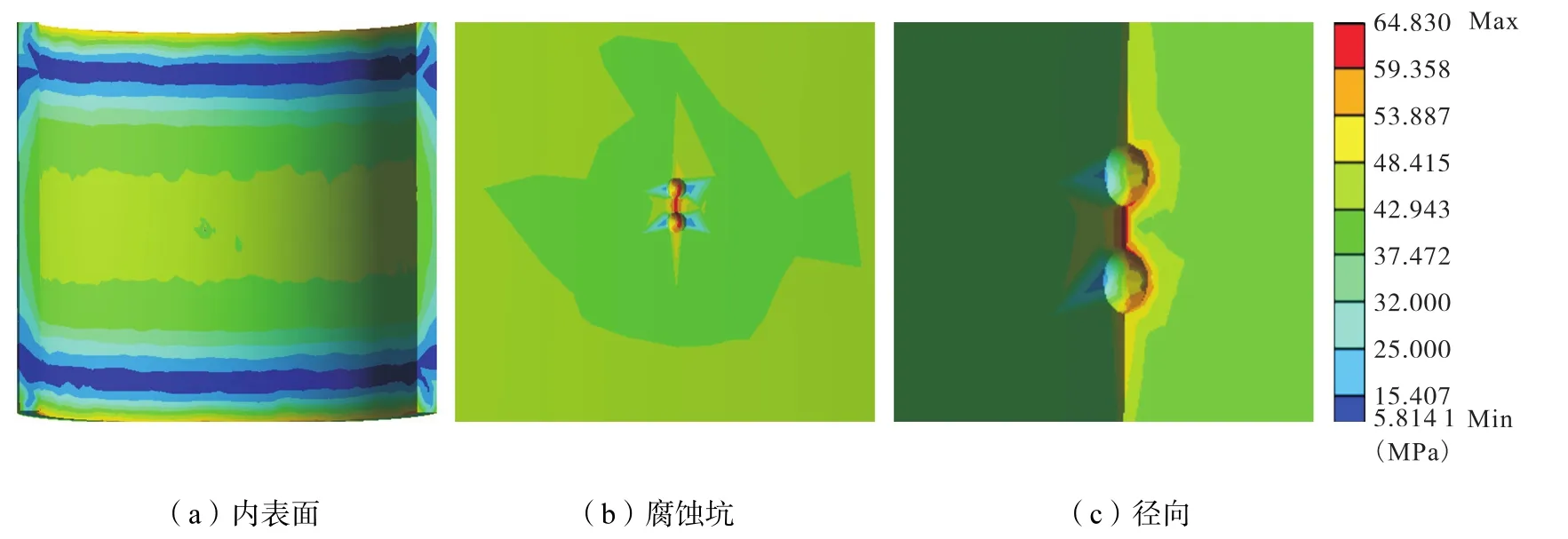
圖4 雙球狀腐蝕(1mm)Fig.4 Double spherical corrosion shapes(1mm)

圖5 雙橢圓狀腐蝕(1mm)Fig.5 Double elliptic corrosion shapes(1mm)

3.6 考慮10年后橢圓腐蝕(深度2 mm)

接下來我們考慮腐蝕 10年后(腐蝕深度 2mm)的套管應力分布情況，從圖6可以看出，僅僅考慮腐蝕深度的變化時，套管中部的應力大小與腐蝕5年相比，應力變大，但變化值很小，橢圓坑周圍的應力變化較大，橢圓坑中心出現最大應力。套管內部部分區域屈服深度變大，套管外部依然正常，并未屈服。

3.7 考慮10年后橢圓加深點腐蝕

從 10年后的腐蝕坑應力分布情況來看，我們考慮了當腐蝕坑中出現腐蝕加深現象時，套管的應力分布情況。對比圖6和圖7可以看出，腐蝕加深與未發生腐蝕加深時，最大應力變大，并且最大應力在腐蝕坑中的分布面積變大。腐蝕坑周圍套管發生的屈服面積較未發生腐蝕加深的腐蝕坑的屈服面積較大，并且深度更深。腐蝕坑周圍應力分布區域最大的應力為 41MPa，套管壁厚的 80%區域并未屈服，套管依然能夠正常運行。

3.8 考慮10年后橢圓擴散腐蝕

在考慮橢圓兩端擴散腐蝕的情況時，從圖8可以看出，橢圓坑受最大應力約為 62.2MPa，并且分布面積更大，擴散點未發生應力集中現象，應力亦較小。從圖8橢圓坑的應力分布推測，橢圓坑繼續腐蝕時，會使橢圓坑加深和沿徑向繼續擴散，圖中其他區域的應力分布與圖 9相比變化不大，所以在腐蝕坑擴散時，套管依然正常運行。

圖6 橢圓腐蝕(2mm)Fig.6 Elliptic corrosion shapes(2mm)

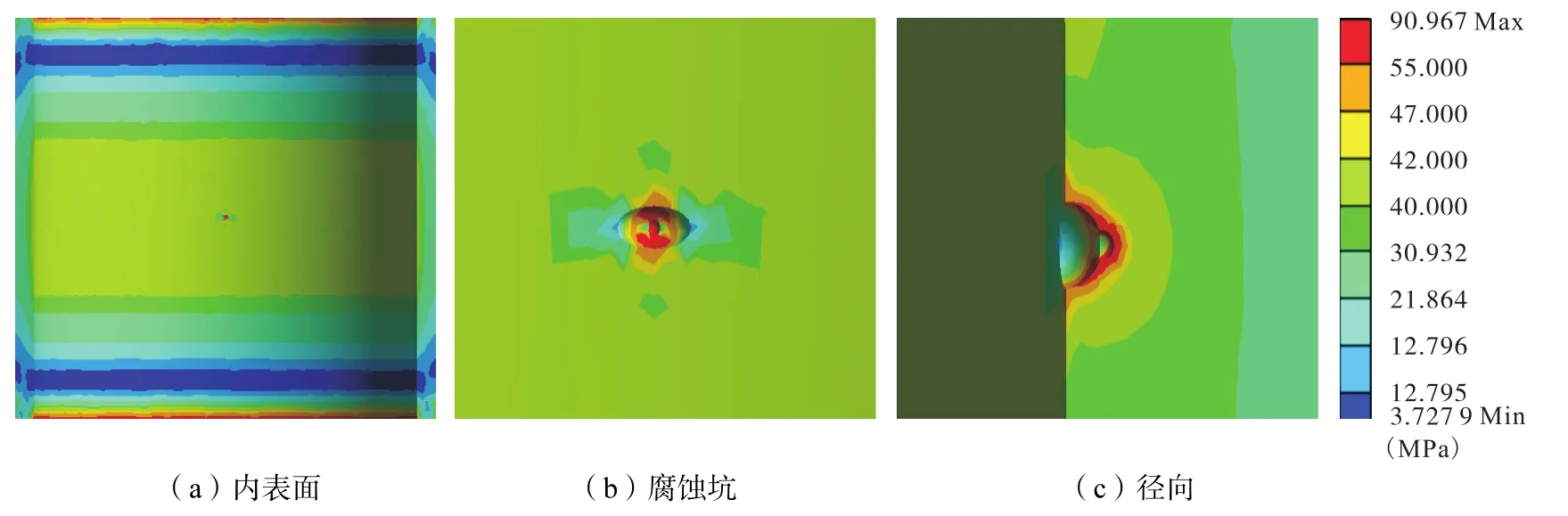
圖7 橢圓加深腐蝕Fig.7 Elliptic deepening corrosion

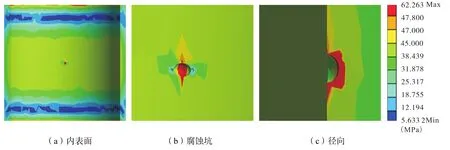
圖8 橢圓擴散腐蝕Fig.8 Elliptic diffusion corrosion

3.9 3 mm橢圓腐蝕

從上述分析中，我們得到了橢圓腐蝕擴散的規律，所以接著考慮按以上規律得到的腐蝕坑(短軸6mm，長軸 10mm)對套管應力分布的影響。從圖 9可以看出，最大應力為 101.27MPa，主要分布在腐蝕坑底部，套管中部的失效面積(應力大于40.7MPa的區域)變大，失效壁厚約 1/3，并且按照理論腐蝕速率，腐蝕 3mm需要 17年，理論上套管并未失效。但是考慮到安全系數與腐蝕速率變化的情況，此時套管已失效，不能正常運行。

3.10 多橢圓點腐蝕

因為腐蝕點坑出現的隨機性，我們考慮了多腐蝕點隨機分布對套管的影響。腐蝕坑大小與圖10中的腐蝕坑相同，從圖中可以看出，失效部分依然出現在套管中部，添加固定約束(螺紋連接區域)周圍的腐蝕點未出現較大的應力分布，套管中部的腐蝕坑的應力分布與圖9中的腐蝕坑應力分布情況相似，最大應力已變大為 104.2MPa。此時套管已失效，不能正常工作。從以上分析我們可以推測出，腐蝕點數量的多少不會影響到應力集中區域(套管的應力集中區域主要分布在螺紋連接處與套管中部)位置的變化，只會影響應力集中區域的應力大小，以及應力的分布深度；同時推測距離螺紋連接最近的區域與套管中部區域易發生腐蝕。

圖9 橢圓腐蝕(3mm)Fig.9 Elliptic corrosion shapes(3mm)

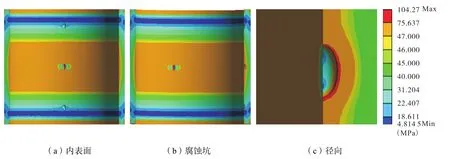
圖10 多點腐蝕Fig.10 Multi-point corrosion

4 套管磨損剩余強度分析

在深井和超深井鉆井過程中，套管磨損是一個日益突出的問題。由于深井和超深井在鉆進過程中需要穿過各種壓力和巖性不同的地層，會導致井眼軌跡變化復雜，使鉆桿與套管間的摩擦不可避免地增加；同時由于鉆桿長度大、剛度小、撓度大等，使得鉆桿在鉆進過程中運動情況變得復雜而與套管間發生接觸、磨損和刮傷，使得套管剩余強度降低。而套管不僅要保證鉆井作業的正常進行，還必須確保套管在鉆井完成后具有足夠的剩余強度以便能夠完成后續的固井、完井以及生產作業。因此，為保證套管的正常使用，對偏磨后套管的應力預測成為油氣田安全生產的關鍵問題之一。套管磨損中常見的非均勻磨損(即偏磨)往往為半月形，如圖11所示。偏磨多是由于各種原因致使套管偏心等導致鉆柱與套管接觸、摩擦，從而在套管內壁的部分區域產生磨損。理想偏磨的磨損部分從套管的橫剖面上看為 2個圓弧面的交集部分，呈月牙形。

從國內外文獻調研情況發現，由于磨損缺陷的不規則性，對磨損后套管應力在理論上進行計算還有一定的難度，一般多數采用有限元法進行數值模擬計算。通過三維有限元軟件 ANSYS 模擬計算得出套管發生非均勻磨損與深度的關系，為評價磨損套管應力提供參考。

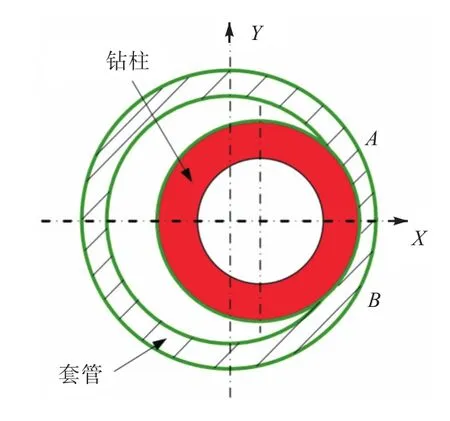
圖11 月牙狀磨損Fig.11 Crescent wear shape

4.1 2 mm深度磨損

首先考慮 2mm偏磨對套管應力分布的影響。從圖12可以看出，半月狀磨損區域存在應力集中現象，同時根據 API套管抗擠與抗壓強度公式可得，抗擠強度 Pco= 51.4MPa ，抗壓強度 Pbo= 47.8MPa ，半月狀區域應力大于 47.8MPa，此區域套管已被壓毀，壓毀厚度約占套管壁厚 1/4，套管外壁最大應力為47MPa，未被擠毀。所以在 2mm 偏磨情況下，套管依然能夠正常運行。

4.2 3 mm深度磨損

接著考慮3mm偏磨對套管應力分布的影響。從圖13可以看出，最大應力并未出現在偏磨區域，但是偏磨區域的應力也大于 49MPa，并且偏磨區域周圍也出現應力大于 49MPa的區域，偏磨區域已經被壓毀，整個偏磨區域的套管壁都發生屈服。偏磨區域周圍的其他區域部分壓毀，盡管壓毀的深度很小，但是因為在偏磨區域套管壁已經完全失效，此時的套管已經不能正常工作。

4.3 4 mm深度磨損

最后考慮了磨損厚度為 4mm(占套管壁厚 1/3)的區域對套管應力分布的影響。從圖14可以看出，最大應力為 97.2MPa，最大應力出現在固定約束區域，偏磨區域的最大應力為 67.4MPa，大于 3mm 深度的偏磨區域最大應力。同時偏磨區域周圍的最小應力為 47.572MPa。應力為 57.517MPa占據的面積較大。因為偏磨區域周圍的最小應力與套管的抗壓屈服強度(47.8MPa)相差很小，所以偏磨區域與偏磨區域輻射到周圍的大部分區域的套管壁都發生屈服。因此可以得出，4mm 深度的偏磨區域會使大部分套管壁都發生屈服，此時套管已不能正常工作。

圖12 2mm半月狀磨損Fig.12 2mm semilunar wear shapes

圖13 3mm半月狀磨損Fig.13 3mm semilunar wear shapes

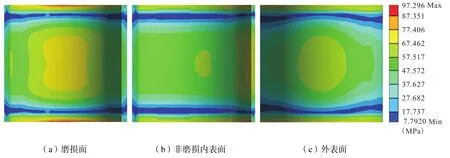
圖14 4mm半月狀磨損Fig.14 4mm semilunar wear shapes

5 結 論

本評估建立以球狀、橢圓狀2種點腐蝕形狀為主的簡化模型，應用有限元方法分析點腐蝕套管的應力分布情況，得到了點腐蝕與套管應力分布的關系，為后續評價腐蝕磨損套管完整性提供了技術基礎。

②根據套管剩余抗擠強度公式和剩余抗壓強度，以及“腐蝕分析-WZ11-1-A23井(YC20190815)”可得出套管理論上正常的運行時間為 19年，但是考慮到抗壓安全系數取為 1.1，所以計算出安全運行時效t≈14年。

③通過有限元方法分析了點腐蝕套管的應力分布情況，得出腐蝕點數量的多少不會影響到應力集中區域(套管的應力集中區域主要分布在螺紋連接處與套管中部)位置的變化，只會影響應力集中區域的應力大小以及應力的分布深度，同時推測距離螺紋連接最近的區域與套管中部區域易發生腐蝕。

④評估了套管磨損中常見的非均勻磨損對該規格套管的應力分布的影響。2mm磨損深度對套管產生了一定的影響，但是套管依然能夠正常運行；3mm磨損深度的偏磨區域已經被壓毀，整個偏磨區域的套管壁都發生屈服，且偏磨區域周圍的其他區域部分壓毀，盡管壓毀的深度很小，但是因為在偏磨區域套管壁已經完全失效，此時的套管已經不能正常工作；4mm磨損深度的偏磨區域與偏磨區域輻射到周圍的大部分區域的套管壁都發生完全屈服，因此可以得出，4mm 深度的偏磨區域會使大部分套管壁都發生屈服，此時套管失效。