單一分形與多重分形軸承故障識別算法的研究

俞凱君 許子非 李春

摘? 要： 分形維是一種可以量化表征事物非線性特性的參數。本文首先介紹了單分形維數和多重分形維數。然后對采集到的高速軸承正常狀態、內環及外環故障時振動信號作小波去噪處理;最后，利用編寫的盒維數、關聯維數及多重分形去趨勢波動法算法，對去噪后的信號進行單一分形與多重分形軸承故障識別分析。結果表明：振動信號具有強多重分形特征，采用多重分形去趨勢波動算法能良好識別軸承故障;對比分析可知，單一分形維在描繪非線性特征方面有局限性，多重分形在刻畫動力學非線性特征方面具有一定的優點。

關鍵詞： 分形維;多重分形;去趨勢波動分析;Hurst指數;軸承故障識別

中圖分類號： TH133? ? 文獻標識碼： A? ? DOI：10.3969/j.issn.1003-6970.2019.10.003

本文著錄格式：俞凱君，許子非，李春. 單一分形與多重分形軸承故障識別算法的研究[J]. 軟件，2019，40（10）：1115

Study on Bearing Fault Identification Algorithm Using Single Fractal and Multifractal

YU Kai-jun， XU Zi-fei， LI Chun*

（School of Energy and Power Engineering， University of Shanghai for Science and Technology， Shanghai 200093， China）

【Abstract】： Fractal dimension is a parameter that can quantify the nonlinear characteristics of things. This paper first introduces the single fractal dimension and the multifractal dimension. Then， the wavelet denoising processing was applied to the collected signals， which include the high-speed bearing under normal state， the vibration signal of the inner ring and the outer ring under fault state; finally， the signal were analyzed for single fractal and multi-fractal bearing fault identification using? box dimension， correlation dimension and multifractal detrended fluctuation analysis （DFA）. The results show that the vibration signal has strong multi-fractal characteristics， and the multi- fractal DFA can identify the bearing fault well. The comparison analysis shows that the single fractal dimension has limitations in depicting the dynamic nonlinear characteristics. Multifractal has certain advantages in characterizing dynamic nonlinear characteristics.

【Key words】： Fractal dimension; Multifractal; Detrended fluctuation analysis; Hurst exponent; Bearing fault identification

0? 引言

近年來，非線性問題得到廣泛關注，分形學也滲透到各個領域，因其具有完備的數學理論及應用價值得到迅速發展。分形維數作為非線性特征的一種表征手段，可有效描述事物的非線性特性，同時，它也可作為一種事物非線性量化度量參數[1]。

分形是指不規則的、分數的物體，可以認為局部和整體存在一定意義上的相似[2]，且具有自相似性與無標度性的特性[3]。分形維數以數值形式的出現，其量化具有直接、簡單、直觀等特點。目前，分形分為單重分形與多重分形兩類。單分形中有許多關于分形維數的定義，包括自相似維數、Hausdorff維數、盒維數、信息維數和關聯維數等。相對于單分形，多重分形定義在在分形上由多個標度指數的奇異測度所組成的無限集合，可反映信號整體分形結構上概率測度分布的比例不均勻性，可提升對信號幾何特性及局部尺度的刻畫精度[4]。

分形維數是軸承故障診斷領域中主要的故障特征量[5]。本研究利用編寫的盒維數、關聯維數及多重分形去趨勢波動法算法，對去噪后的信號進行單一分形與多重分形軸承故障識別分析。

1? 單分形維數

1.1? 盒維數

基于集合覆蓋思想所提出的盒維數計算因計算過程簡單而被應用廣泛。設是的非空有界子集，記表示最大直徑為且能覆蓋集合的最少個數，則的盒維數定義為[6]：

（1）

設離散信號，是維歐式空間上的閉集。用盡可能細的網格劃分，是集合的網格數。由于式（1）無法直接按定義求出，因此計算時采用近似的方法。以網格為基準，逐步放大到網格，其中。

（2）

（3）

式中：;為采樣點數; ;為離散空間上的集合的網格計數。

在圖中確定選取線性較好的一段為無標度區，設無標度區的起點和終點分別為、，則：

（4）

最后，用最小二乘法對數據進行擬合求得該直線的斜率：

（5）

盒維數為：

（6）

1.2? 關聯維數

關聯維數從點與點之間相關性出發，可反映集合各數據點的相關性。1983年，最早由Grassberger和Procaccia根據嵌入理論和重構相空間思想，提出了一種由時間序列直接計算關聯維數D的算法，即G-P算法[7-8]。

長度為N的時延法可以構成長度為、維數為m的相空間。重構相空間的維數m稱為嵌入維數。設原始信號時間序列為，重構相空間矩陣可表示為

（7）

式中，為延遲時間;，為重構相空間中向量的個數，。關聯維數可由式（2）導出，即：

（8）

式中，;H為Heaviside函數， ;r為相空間中超球半徑;為兩矢量間距離。是信號的相關積分，與r存在以下關系：

（9）

式中，當時，為關聯維數，為：

（10）

2? 多重分形

多重分形對于單分形，從多尺度角度刻畫非線性程度[9]。

2.1? 廣義Hurst指數

針對振動信號時間序列，MF-DFA[10]計算步驟如下：

（1）求振動信號時間序列對于均值的累積離差：

（11）

式中：為時間序列的均值。

（2）將劃分為長度為s的m個等長子區間，m=int（N/s）。由于N不一定整除s，因此再從的反方向重復這一過程，即得到2m個等長子區間。

（3）采用最小二乘法擬合每一子區間的均方誤差。當時，

（12）

當時，

（13）

式中：是第v個子區間的r階擬合多項式，擬合階數r反映了“趨勢”被消除的程度，階數越高，“趨勢”消除效果越好，但會增加計算時間。

（4） 對2m個子區間，定義q階波動函數為：

（14）

當q=2時，MF-DFA即為標準DFA方法。

（5）改變子區間長度s的大小，重復步驟（1）～（4）。若時間序列存在長程相關性，則q階波動函數與s之間存在如下冪律關系：

（15）

若時間序列只具有單重分形特性時，廣義Hurst指數為常數，且當時間序列不相關或短程相關時，=1/2;當時間序列存在多重分形特性時，與q呈非線性關系。

2.2? 多重分形譜

根據標準配分函數可得標度指數，其與廣義Hurst指數之間的關系為：

（16）

根據統計物理中的Legendre變換式，可得奇異指數和譜函數分別為：

（17）

（18）

將式（16）代入式（17）和式（18），可得多重分形譜奇異指數和譜函數與廣義Hurst指數之間的關系如下：

（19）

（20）

根據譜函數可判斷時間序列分形特征。當為常數時，時間序列具有單重分形特征;若變化規律為單峰值曲線，則該時間序列具有多重分形特征，將的區間記為。

3? 實驗數據分析

3.1? 數據來源及處理方法

通過對風力機增速箱中加裝傳感器，分別采集高速軸軸承正常狀態、內環及外環故障時振動信號，采樣頻率為1000 kHz。通過MATLAB2018b編程實現對信號的小波去噪，自編寫盒維數、關聯維數及多重分形去趨勢波動法算法，處理去噪后的信號并進行結果比對。

3.2? 數據降噪處理

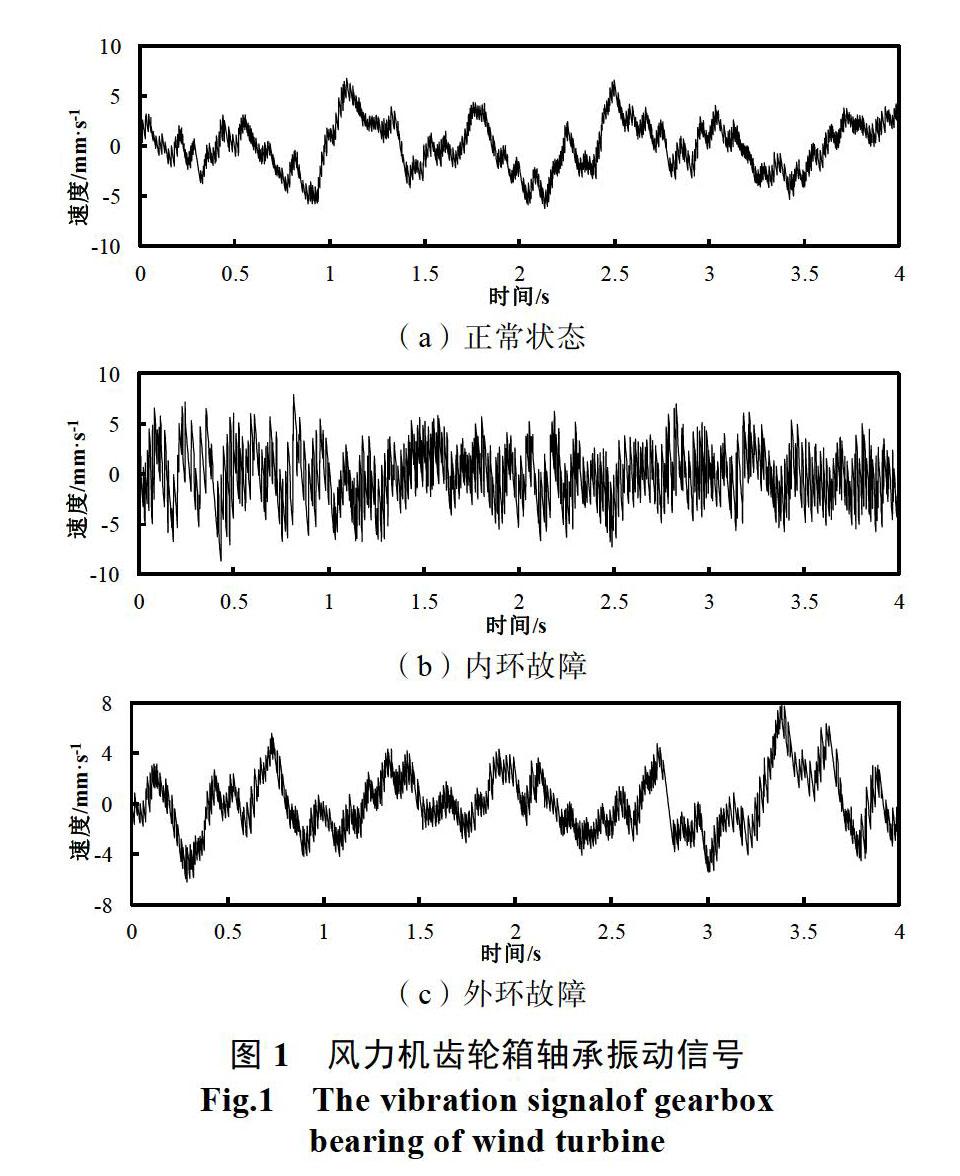
采用小波降噪方法，對軸承三種狀態進行降噪處理，處理前后的正常狀態，發生內環及外環故障時振動信號如圖1與圖2所示。

由圖1與圖2可知，未經處理的正常、內圈及外圈軸承振動信號的最大值分別為6.75 m·s–1、7.85 m·s–1及7.83 m·s–1;經小波降噪處理后的最值分別為6.6 m·s–1、7.15 m·s–1及7.38 m·s–1，使得正常與故障間區分度變大。

3.3? 盒維數分析

由表可知，三種狀態的分形維數各不相同，其中內環故障分形盒維數最小，外環故障的分形盒維數最大，但是僅單分形盒維數難以區分正常及外環故障的狀態。

3.4? 關聯維數分析

對不同狀態的軸承振動信號進行關聯維數分析，不同嵌入維數m下的變化關系曲線如圖3所示，軸承不同工作狀態下振動信號關聯維數隨嵌入維數變化關系如圖4所示。

如圖3可知，較大尺度導致關聯積分保持不變，雙對數曲線平行與坐標軸，并稱其為無標度區間，采用最小二乘擬合法得到關聯位數。

由圖4可知，當嵌入維數大于24時，關聯維數趨于穩定。軸承處于不同狀態時，其振動信號關聯維數亦有所不同。軸承處于正常狀態時，取兩位有效數字，其振動信號關聯維數為4.0;而當軸承分別發生內環或外環故障時，其振動信號關聯維數分別為3.0與4.7。因此，關聯維數較分形盒維數可較好區分故障狀態。

3.5? 廣義Hurst指數分析

采用多重分形去趨勢波動法分析三種軸承狀態，其廣義Hurst指數隨標度變化如圖5所示。

由圖5可知，廣義Hurst指數隨q非線性變化，表明振動信號具備多重分形特征，且可良好區分三種狀態。

3.6? 多重分形譜分析

在分析振動信號的標度指數與廣義Hurst指數后，可明顯判定風力機齒輪箱軸承振動信號具有典型的多重分形特性。計算振動信號多重分形譜，其結果如圖6所示。

風力機齒輪箱軸承振動信號的多重分形譜均呈單峰鐘形，此特點充分說明振動信號具有明顯的多重分形特性，且不同波形相差明顯，可區分不同的軸承狀態。

4? 結論

本文采用兩種單重分形算法（盒維數與關聯維數）對不同工作狀態軸承信號進行分析，同為描述非線性特征的盒維數僅能區別內圈故障信號與其余狀態，但關聯維數在區分三種故障狀態時表現較好。又采用多重分形去趨勢波動方法刻畫振動信號在不同標度下廣義Hurst指數變化與多重分形譜，結果表明：振動信號具有強多重分形特征，且能良好區分軸承三種工作狀態;對比分析可知，單一分形維在一定程度上難以準確描繪出非線性特征，多重分形在刻畫動力學非線性特征方面具有一定的優點。

參考文獻

[1]Candela R， Mirelli G， Schifani R， et al. PD recongnition by means of statistical and fractal parameters and neural net work， IEEE Transactions on Dielectrics and Electrical Insu-

lation， 2007， 7（1）： 87-94.

[2]陳颙. 分形幾何學[M]. 北京： 地震出版社， 1998： 12-48.

[3]Falconer K J. Fractal geometry： Mathematical Foundations and Applications[M]. Chichester： John Wiley&Sons Ltd， 1990： 40-60.

[4]劉彬， 王霄， 謝平. 基于小波多重分形的復雜機械故障診斷方法研究[J]. 傳感技術學報， 2006， 19（1）： 232-234.

[5]李洋， 李春， 楊陽， 袁全勇. 基于分形學的軸承故障診斷分析[J]. 熱能動力工程， 2017， 32（12）： 73-77+140.

[6]Sarkar N， Chaudhuri B B. An efficient differential box- counting approach to compute fractal dimension of image[J]. IEEE Transactions on Systems Man & Cybernetics， 1994， 24（1）： 115-120.

[7]Grassberger P， Procaccia I. Estimation of the Kolmogorov entropy from a chaotic signal[J]. Physical Review A， 1983， 28（4）： 2591-2593.

[8]姜萬錄， 陳東寧， 姚成玉. 關聯維數分析方法及其在液壓泵故障診斷中的應用[J]. 傳感技術學報， 2004， 17（1）： 62-65.

[9]Falconer， K. J. Fractal geometry-mathematical foundations and applications[J]. Biometrics， 2014， 46（3）： 499.

[10]Rizvi S A R， Dewandaru G， Bacha O I， et al. An analysis of stock market efficiency： Developed vs Islamic stock markets using MF-DFA[J]. Physica A Statistical Mechanics & Its Applications， 2014， 407： 86-99.

[11]張樂玫， 羅濤. 室內定位特征選擇算法研究[J]. 軟件， 2015， 36（1）： 38-46.

[12]陳驍睿. 基于改進粒子群算法的機位分配問題研究[J]. 軟件， 2015， 36（1）： 72-76.

[13]蔣然， 張光桃. 基于預分類的逆變異分類器算法[J]. 軟件， 2015， 36（2）： 39-44.