淺談線性規劃在實際生活中的應用

曹亞群

（安徽水利水電職業技術學院，安徽合肥 231603）

1 什么是線性規劃

線性規劃是運籌學的重要分支，是合理分配及利用有限資源，以取得最佳經濟效益的一種優化方法。它采取的是在一系列條件約束下，獲得最優值的數學理論[1]。線性規劃是一種數學規劃方法，滿足約束條件下，讓目標函數取得最優值。它要解決的問題通常約束條件及目標函數是線性關系，約束條件是不等式或者等式，目標函數取極值。線性規劃在管理學、建筑學、經濟學等領域都有著廣泛的應用，例如：下料問題、庫存問題、運輸問題等。線性規劃都有一定的形式，標準形式如下：

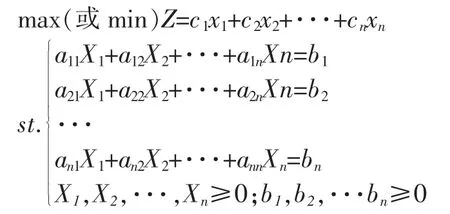
2 線性規劃在實際生活中的應用

在我們的實際生活中，可以利用線性規劃解決很多問題以減少人們的工作量、節約經費，提高工作效率[2]。生活中一些常見問題，比如兩種不同型號材料的配比問題、話費選用套餐問題等，都可以用線性規劃這種統籌方法找到最優解。下面，我們就以生活中某些常見問題為例，說明線性規劃在實際生活中的應用。

2.1 線性規劃在合理下料問題中的應用

合理下料問題是線性規劃模型中的典型問題，建筑施工中，需要大量的各種各樣的原材料，比如：鋼材、木材、鋁合金、砂、石、塑鋼等建筑材料，而生產廠家只能提供一定規格的原材料，實際施工時要裁減才能得到所需要的規格，這樣必然會產生殘料，造成一定的損失和浪費，所以，合理下料，盡量減少產生殘料，這讓建筑企業能夠減少成本投入，獲得更高的經濟效益[3]。下面，選用一個例子來說明線性規劃在下料問題中的實際應用。

問題：要把20 根4 m 長和25 根5 m 長的同規格鋼材，截成1.5 m 的50 根，1.2 m 的80 根，如何下料廢料最少?(所有下料方法見表1)

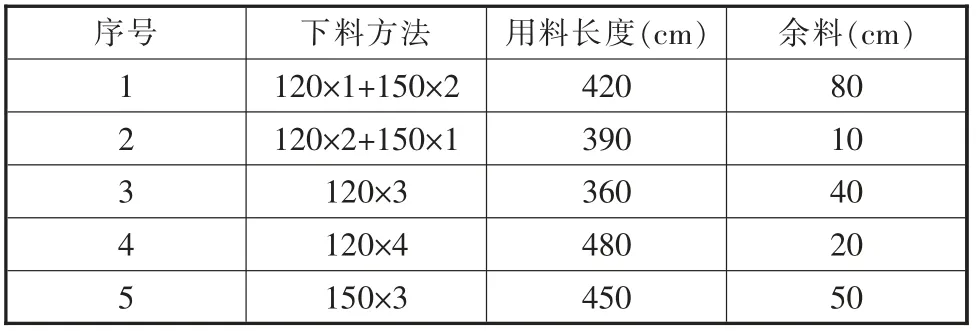
表1 下料方法

解：設用以上五種方法分別各用X1，X2，X3，X4，X5，次，則min f（X）=80X1+10X2+40X3+20X4+50X4

運用LIND0 軟件，解得X1=0，X2=20，X3=0，X4=10，X5=10，即方法2 用20 次，方法4 用10 次，方法5 用10次，廢料最少為900 cm。

2.2 線性規劃在廣告投放問題中的應用

如今，隨著人民生活水平的不斷提高，幾乎每家都有電視，電視的普及率已經相當高了。尤其是目前手機、 電腦等電子產品的普及更是讓人們感受到科技的力量。鑒于此，很多商家將目光投向了各種應用媒體平臺的廣告時段，目的就是增加自己的產品在人們視線中的出現頻率。各個廣告投資商需要根據具體情況，弄清楚各個媒體平臺播放廣告的時間及所需資金，以便獲得更大的利潤[4]。接下來我們用實際生活中的例子進行舉例分析。

問題：某商家在投入資金不超過80 萬元的條件下，需要保證至少有200 萬女性觀眾觀看廣告，其中在電視臺投入的廣告費用不超過50 萬元，電視臺在白天至少播出3 次，在晚上至少播出2 次，無線電廣播和雜志的廣告播放次數均不低于5 次且不超過10 次,廣告市場調查結果如表2 所示，問要想獲得理想的廣告效果應該如何安排播放次數。

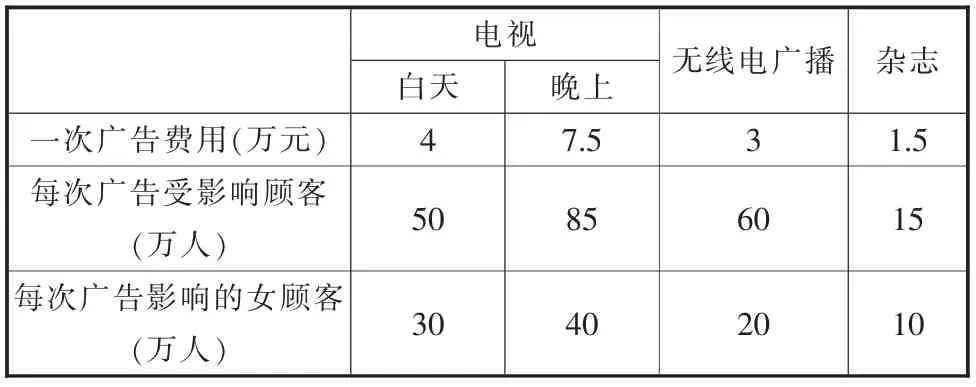
表2 廣告市場調查結果

解：設電視臺的廣告在白天的播放次數為X1次，晚間的播放次數為X2，無線電廣播播放X3次，雜志的廣告刊登為X4次。則：

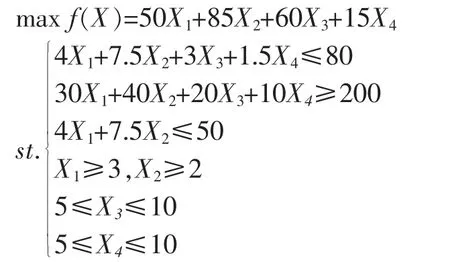
運用LIND0 軟件，解得X1=3，X2=3，X3=10，X4=10，此時，總觀看人數是1 155 萬人，女性觀看人數是510萬人，總支出是79.5 萬元。

2.3 在集合料問題中應用

解決集合料問題必須滿足一定的條件，如種類、含量等，用數學語言表達各個條件，就是線性規劃模型中的約束條件，要求所用的運輸費用最省，用數學語言表達，就是線性規劃模型中的目標函數，在集合料問題中，有很多不同方案被選擇，優化目的就是從眾多方案中選出一個最優方案[5]。

問題：某個筑路工地鋪設道路基層，需要10 000 m3集合料，準備從兩個棄土堆取混合料，已知棄土堆A 的材料成分為：礫石含量70%，砂含量30%，棄土堆B 的材料成分為：礫石含量30%，砂含量60%，粘土含量10%，集合料的成分含量要求為：礫石含量60%,砂含量50%，粘土含量8%。從棄土堆A 取料的裝載運輸費為2元/m3，從棄土堆B 取料的裝載運輸費為3.2 元/m3。問應如何取料才能使總的運輸費用最少?

解：設從棄土堆A、B 取料數量分別為X1、X2m3，則：

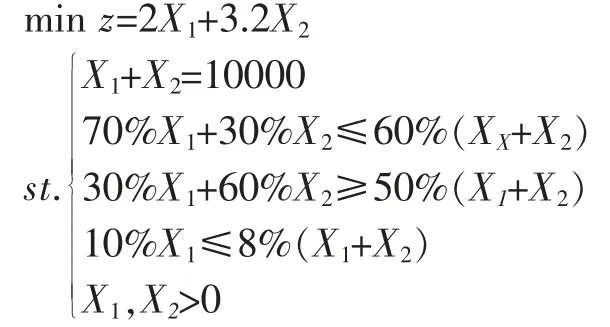
解得:X1=3 333 m3，X2=6 667 m3即從棄土堆A取料3 333 m3，從棄土堆B 取料6 667 m3，這樣配料裝卸運輸費用最少為28 000 元。

3 結語

線性規劃是有力的數學工具，它的重要目標就是規劃出各種“最優”，即如何用最佳的方式分配有限的資源，以獲得最佳經濟效益，如施工建筑下料問題中節約了材料，盡量減少殘料的發生，合理下料，投資廣告問題中獲得預期的廣告效果，集合料問題中如何取料運輸費用最少，線性規劃在諸如這些生活中的具體應用還有很多很多。