太陽帆航天器在繞地軌道中的熱誘發振動

張軍徽，佟安，武娜，劉應華

1.北方工業大學 土木工程學院，北京 100144 2.清華大學 航天航空學院，北京 100084

光對被照射物體的壓力稱為光壓。依靠光壓推進的太陽帆航天器無需消耗推進劑，可以實現傳統航天器無法實現的各種非開普勒軌道，被認為是最可行的星際探測技術。2010年日本IKAROS號太陽帆[1]和2011年美國Nanosail-D號太陽帆[2]的相繼成功發射把人類星際旅行的夢想照進了現實。繞地球飛行軌道是太陽帆進入星際軌道的起點，更是各種近地球任務太陽帆運行的主要場所。太陽帆在繞地軌道中將會周期性地進出地球陰影，經歷熱環境的劇烈變化，在熱輻射沖擊作用下，太陽帆這種大柔性空間結構的熱致響應值得研究。

熱致結構響應的研究最早可以追溯到1956年，Boley在熱致結構響應分析中引入慣性項，提出了熱誘發振動的概念[3]。熱誘發振動影響航天器正常工作的事件屢有發生，其中，最為著名的是太陽翼熱誘發振動造成的哈勃太空望遠鏡成像模糊畸變事故。Thornton和Kim考慮結構變形對熱載荷的影響，建立了太陽翼的熱-結構耦合動力學模型，數值再現了哈勃望遠鏡太陽翼在突加熱流載荷作用下的彎扭耦合熱誘發振動[4]。Gulick和Thornton研究了自旋穩定衛星軸向天線的熱誘發振動，研究表明：當衛星的自旋速度等于天線的彎曲振動頻率，衛星天線將發生不穩定的熱誘發振動，即熱顫振[5]。Song等研究了復合材料薄壁梁的熱誘發振動穩定性問題[6]。Zhao等推導了考慮熱輻射的復合材料板的有限元方程，為分析航天器柔性復合材料薄板附件的熱誘發振動提供了工具[7]。Shen等基于絕對節點坐標方法推導了梁的熱-結構耦合方程，得益于絕對節點坐標方法的優點，該方程不但能計算晝夜轉換熱沖擊引起的梁熱顫振，也能計算由于大轉動引起的梁熱誘發振動[8]。Zhang等在Graham和Thorton等工作的基礎上，建立了懸臂梁在空間熱輻射作用下的熱顫振準則：若空間熱流入射角大于梁自由端的準靜態轉角，則熱顫振不會發生[9]。Li和Yan研究了蜂窩復合材料太陽翼在近地軌道的熱誘發振動[10]。Su等在空間環境模擬器中對復雜桁架的熱致響應進行了實驗研究，成功觀測到了空間桁架的熱誘發振動[11]。Wang和Li研究了熱載荷作用下索-梁結構的參激振動[12]。Shen和Hu研究了熱誘發振動對自旋穩定航天器姿態的影響，數值結果表明熱誘發振動引起了Ulysses衛星姿態角的跳變[13]。Liu和Pan建立了剛-柔-熱耦合的多體動力學模型，考慮太陽熱輻射和地球熱輻射等的影響，研究了帶有柔性太陽翼航天器在近地軌道的熱誘發振動[14]。Chen等研究了預應力對復合材料薄板熱誘發振動的影響[15]。Azadi等研究了近地軌道衛星的壓電智能太陽帆板的熱誘發振動[16]。Liu等研究了熱結構耦合作用下柔性航天器的姿態控制問題[17]。Xue等提出了傅立葉溫度單元方法，大大提高了薄壁結構非線性溫度場的求解效率，并將該方法用于大型柔性空間結構的熱-結構耦合分析中，促進了熱致結構響應分析的工程應用[18-20]。

目前，國內外關于太陽帆的研究集中在總體設計[21-22]、軌道和姿態控制[23-27]、帆膜制備和展開[28-30]等方面。按照展開和維持帆面構型的方式不同，太陽帆總體設計可分為旋轉展開無桅桿式和機械展開有桅桿式兩大類，圖1所示為NASA研制的方形有桅桿式太陽帆[2]。通常認為有桅桿式太陽帆具有展開可靠性高，姿態控制簡單和消耗控制能量小等優點[31]。但是，有桅桿式太陽帆在繞地軌道熱輻射沖擊作用下，桅桿截面溫差可能引起太陽帆結構的熱致響應，從而影響太陽帆順利進入星際軌道，或者影響近地球任務太陽帆的工作性能。目前，國內外關于有桅桿式太陽帆在繞地軌道中的熱誘發振動問題未見報道。

圖1 NASA研制的Nanosail-D太陽帆[2]Fig.1 Solar sail Nanosail-D designed by NASA[2]

本文以方形有桅桿式太陽帆為研究對象，考慮熱輻射等非線性因素，建立太陽帆的熱-結構耦合動力學模型，分析太陽帆在繞地軌道中遭受熱輻射沖擊作用時的結構動力學響應，為繞地軌道太陽帆的結構設計、軌道設計和姿態控制提供理論依據。

1 模型與假設

本文以正方形五點連接式太陽帆為研究對象，總體結構如圖2所示，三角形薄膜帆面通過張拉索與對角線桅桿連接，帆面薄膜(簡稱：帆膜)在預應力作用下保持平整，有效載荷安裝在太陽帆中心。

圖2 五點連接式方形太陽帆Fig.2 Five-point suspension square solar sail

本文太陽帆熱-結構耦合分析采用如下假設：

1) 光壓很小，太陽帆結構發生小變形。

2) 帆膜褶皺幅值較小，忽略褶皺對光壓壓心位置和帆膜吸熱的影響。

3) 帆膜通過張拉索與桅桿相連，忽略桅桿與帆膜之間的熱傳導。

4) 太陽帆結構對稱。

2 太陽帆的熱-結構耦合動力學方程

太陽帆由地球陰影區進入光照區，桅桿-帆膜結構的溫度場在突加太陽熱流的作用下將發生瞬態變化。由于熱彈性效應，薄壁桅桿和帆膜的瞬態溫度變化將在桅桿和帆膜內部產生沖擊熱應力，進而引發太陽帆結構的動力學響應。本節建立太陽帆桅桿-帆膜結構的熱-結構動力學方程。

2.1 瞬態熱傳導方程

太陽帆進入光照區后，薄壁桅桿受到太陽輻射熱流S0的作用如圖3所示，(O,x,y,z)為桅桿局部坐標系;θ0為太陽輻射熱流入射方向與桅桿外表面法線的夾角;h為桅桿截面壁厚。

圖3 太陽輻射熱流作用下的太陽帆薄壁桅桿Fig.3 Thin-walled boom subjected to solar heat flux

忽略沿桅桿壁厚方向的溫度變化，薄壁桅桿的溫度場為二維分布：T(x,φ,t)，滿足如下非線性偏微分方程：

(1)

式中：c為桅桿比熱；ρ為桅桿密度；t為時間；R為桅桿截面的平均半徑；φ為桅桿截面壁厚中線的周向角坐標；kx，kφ分別為桅桿沿x向，φ向的熱傳導系數；ε為桅桿外表面的熱輻射系數；σ為Stefan-Boltzman常數；q為桅桿外表面吸收的太陽輻射熱量：

(2)

其中：αs為桅桿外表面的熱輻射吸收系數；S0為太陽輻射熱流S0的幅值。

將T(x,φ,t)在桅桿截面內的分布近似為截面平均溫度Ta(x,t)和截面攝動溫度Tp(x,t)的疊加[4]：

T(x,φ,t)≈Ta(x,t)+Tp(x,t)cosφ

(3)

將式(3)代入式(1)，并在桅桿截面內進行積分，可將式(1)解耦為如下2個偏微分方程：

(4)

(5)

式中：k為熱傳導系數。其初始條件為：Ta(x,t0)=T0和Tp(x,t0)=0，其中T0為太陽帆結構初始溫度，t0表示初始時刻。

太陽輻射熱流S0作用下，帆膜的溫度場也將發生變化。考慮到帆膜厚度很小，忽略膜厚方向的溫度變化，且不考慮褶皺對吸熱的影響，則帆膜溫度場在整個帆膜結構內均勻分布：Tm(t)，滿足如下微分方程：

(6)

其初始條件為：Tm(t0)=T0。式中：cm為帆膜比熱；ρm為帆膜密度；εm為帆膜表面的熱輻射系數；αm為帆膜表面的吸收系數；tm為帆膜厚度。

式(4)～式(6)即為描述太陽帆桅桿-帆膜結構瞬態溫度場的熱傳導方程。

2.2 結構動力學方程

由于熱彈性效應，截面平均溫度Ta的升降將引起桅桿沿軸向的伸縮變形，截面攝動溫度Tp的變化將引起桅桿的彎曲變形，這些變形可等效為分別由外載荷熱軸力FT和熱彎矩MT引起的，其計算公式為

眾創空間是集聚創客、高校、企業和科研機構等各類主體的協同創新合作體系，可以實現跨行業跨領域的創新資源彈性配置，并形成聚合效應和疊加效應。它不僅為創客團隊提供了實現突破性創新的要素和資源，還為協同創新搭建了深度互聯的網絡服務平臺，有助于創客團隊進行全向度創新。而且眾創空間在協同創新過程中能夠不斷演化，形成正反饋鏈條，從而加速產品創新和迭代速度，打造出融合、開放、多元的協同創新生態圈。

FT=αTEA(Ta-T0)

(7)

(8)

式中：αT為桅桿熱膨脹系數；A為桅桿截面面積；E為桅桿彈性模量；I為桅桿截面關于z軸的慣性矩。

對于帆膜結構，由于帆膜厚度很小，帆膜厚度方向的溫差變化無法形成帆膜熱彎矩，因而不會引起帆膜的熱誘發振動，但是，帆膜溫度Tm將引起帆膜預應力的變化，從而影響張拉索作用在桅桿上的拉力Fm。

根據對稱性，太陽帆桅桿可看作為薄壁懸臂梁結構，其受到熱軸力FT、熱彎矩MT和張拉索拉力Fm的作用，如圖4所示。

采用Euler-Bernoulli梁理論，太陽帆桅桿在熱載荷作用下的運動方程為

(9)

圖4 熱應力作用下的太陽帆薄壁桅桿Fig.4 Thin-walled boom subjected to thermally- induced loads

需滿足的邊界條件為

w(0,t)=0

(10a)

(10b)

(10c)

(10d)

設w(x,t)可近似表示為

w(x,t)=W1(t)N1(x)+W2(t)N2(x)

(11)

式中：W1(t)和W2(t)為廣義位移；N1(x)和N2(x)為形函數。考慮強制邊界條件式(10a)和式(10b)，可取N1(x)=x2，N2(x)=x3。

采用伽遼金加權余量法，分別取罰函數為N1(x)和N2(x)，考慮到邊界條件式(10c)和式(10d)，可得式(9)的等效積分格式：

+N1(l)[EIw″(l,t)+MT(l,t)]+

N1(l)[EIw′″(l,t)+Fe]=0

(12)

+N2(l)[EIw″(l,t)+MT(l,t)]+

N2(l)[EIw′″(l,t)+Fe]=0

(13)

將式(11)分別代入式(12)和式(13)，并在桅桿域內分部積分，可得

(14)

式中：

式(14)和式(4)～式(6)共同構成了描述太陽帆桅桿-帆膜結構熱誘發振動的熱-結構耦合動力學方程組。

2.3 熱-結構動力學方程的求解

太陽帆桅桿-帆膜結構的熱-結構耦合動力學方程組可采用直接積分法求解，由于熱輻射項的存在，其中式(4)和式(6)是非線性的，在每個時間步還需要迭代求解，其具體求解流程如圖5所示。

圖5 熱-結構耦合動力學方程的求解流程Fig.5 Solving algorithm of thermal-structure coapling dynamic equations

按照上述求解流程，本文使用Visual-Fortran 90編寫了太陽帆桅桿-帆膜的熱-結構動力學計算程序。

3 太陽帆的熱誘發振動分析

文獻[4]考慮桅桿靜態變形、屈曲載荷、總質量等約束條件，以太陽帆特征加速度達到1 mm/s2為目標給出了邊長100 m的方形太陽帆優化設計方案，本文對該太陽帆方案進行熱致結構響應分析，其結構尺寸和材料參數見表1和表2。

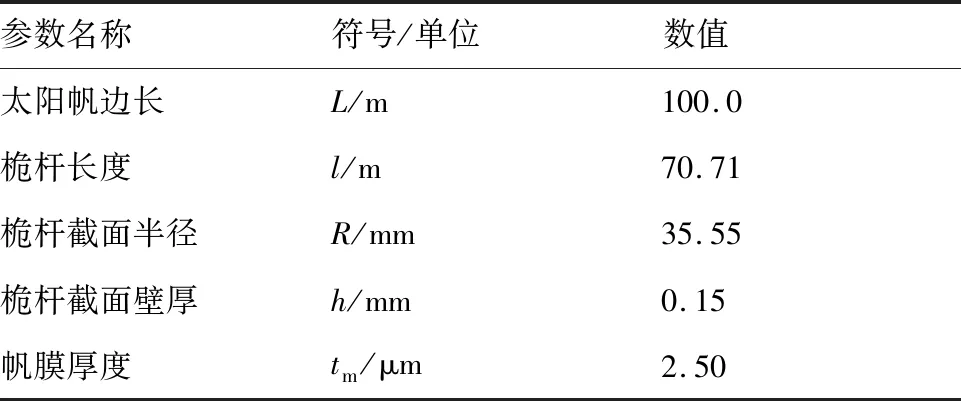
表1 太陽帆結構尺寸Table 1 Structural dimensions of solar sail

表2 太陽帆材料參數Table 2 Material parameters of solar sail

太陽帆繞地運行，由地球陰影進入光照區，受到突加太陽熱流S0=1 350 W/m2和突加光壓P0=9.12×10-6Pa的作用。

3.1 太陽帆的熱致結構動力學響應

以太陽帆進入光照區為初始時刻t0=0 s，設太陽帆桅桿截面初始平均溫度Ta(x,0)=290 K,初始攝動溫度Tp(x,0)=0 K，熱流入射角度為0°。

圖6為太陽帆桅桿截面平均溫度隨時間變化的歷程圖，桅桿截面平均溫度Ta在太陽輻射熱流作用下緩慢上升，在t=450 s后達到穩態溫度413 K。

圖6 桅桿自由端截面平均溫度時間歷程Fig.6 Variation of average temperature of boom cross-section with time

圖7為太陽帆桅桿截面攝動溫度隨時間變化的歷程圖，桅桿截面攝動溫度Tp在太陽輻射熱流作用下快速上升，在t=250 s后達到穩定，桅桿截面最大溫差達到了92.98 K。

圖7 桅桿自由端截面攝動溫度時間歷程Fig.7 Variation of perturbation temperature of boom cross-section with time

圖8給出了桅桿自由端截面內的溫度變化，可以看出桅桿溫度在截面內的正弦分布，光照面的最大溫度達到了496 K，背光面的溫度為329.9 K，桅桿截面內的溫差達到了166 K。

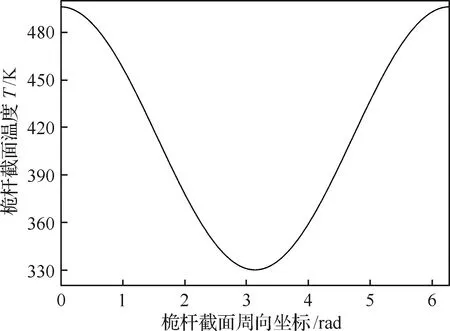
圖8 桅桿自由端截面溫度分布Fig.8 Temperature distribution on cross-section of boom tip

太陽帆桅桿截面內的溫差將引起熱彎矩，其作用在桅桿上會引起太陽帆桅桿的動態響應，圖9給出了沖擊熱彎矩引起的桅桿自由端位移時間歷程。

圖9 桅桿自由端的位移-時間歷程Fig.9 Displacement-time history of boom tip

由圖9可以看出，在太陽輻射熱沖擊作用下，太陽帆桅桿發生了明顯的熱誘發振動，振動形式為圍繞準靜態變形的等幅振動，其準靜態變形為3.16 m，平均振幅為0.75 m，最大動態位移達到了4.10 m。

3.2 太陽帆熱誘發振動的參數分析

太陽帆發生熱誘發振動的條件和特點取決于太陽帆結構剛度、進入光照區的姿態角和帆膜預應力等因素，本小節對這些影響太陽帆熱誘發振動的因素進行參數分析。

太陽帆進入光照區的姿態會造成太陽輻射熱流相對于結構的入射角θ0不同，從而影響結構吸收熱量的不同。圖10為不同熱流入射角下，桅桿平均溫度隨時間變化的歷程圖，可以看出隨著輻射熱流由垂直入射變為斜射，桅桿表面吸收熱量減少，太陽帆桅桿截面平均溫度Ta的穩態值變小：由垂直入射θ0=0°的時的413.1 K，逐漸減小為θ0=75°的時的294.5 K。圖11為不同熱流入射角下，桅桿截面攝動溫度隨時間變化的歷程圖，同樣，隨著熱流由垂直入射變為斜射，桅桿截面的溫差Tp也逐漸減小：由垂直入射θ0=0°時的83.2 K，逐漸減小為θ0=75°時的32.0 K。

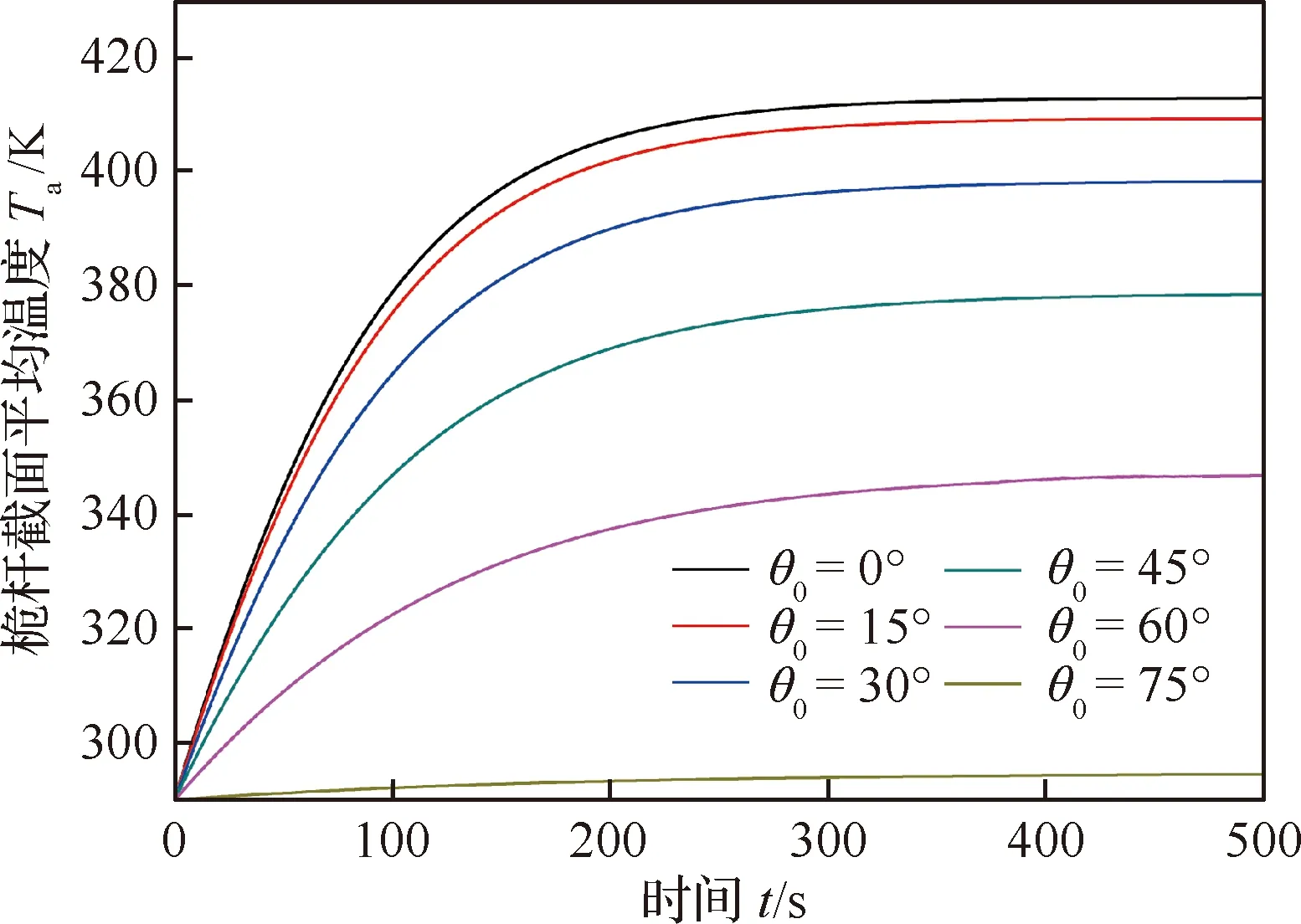
圖10 熱流入射角度對桅桿截面平均溫度的影響Fig.10 Effect of incident angle of heat flux on average temperature of boom cross-section

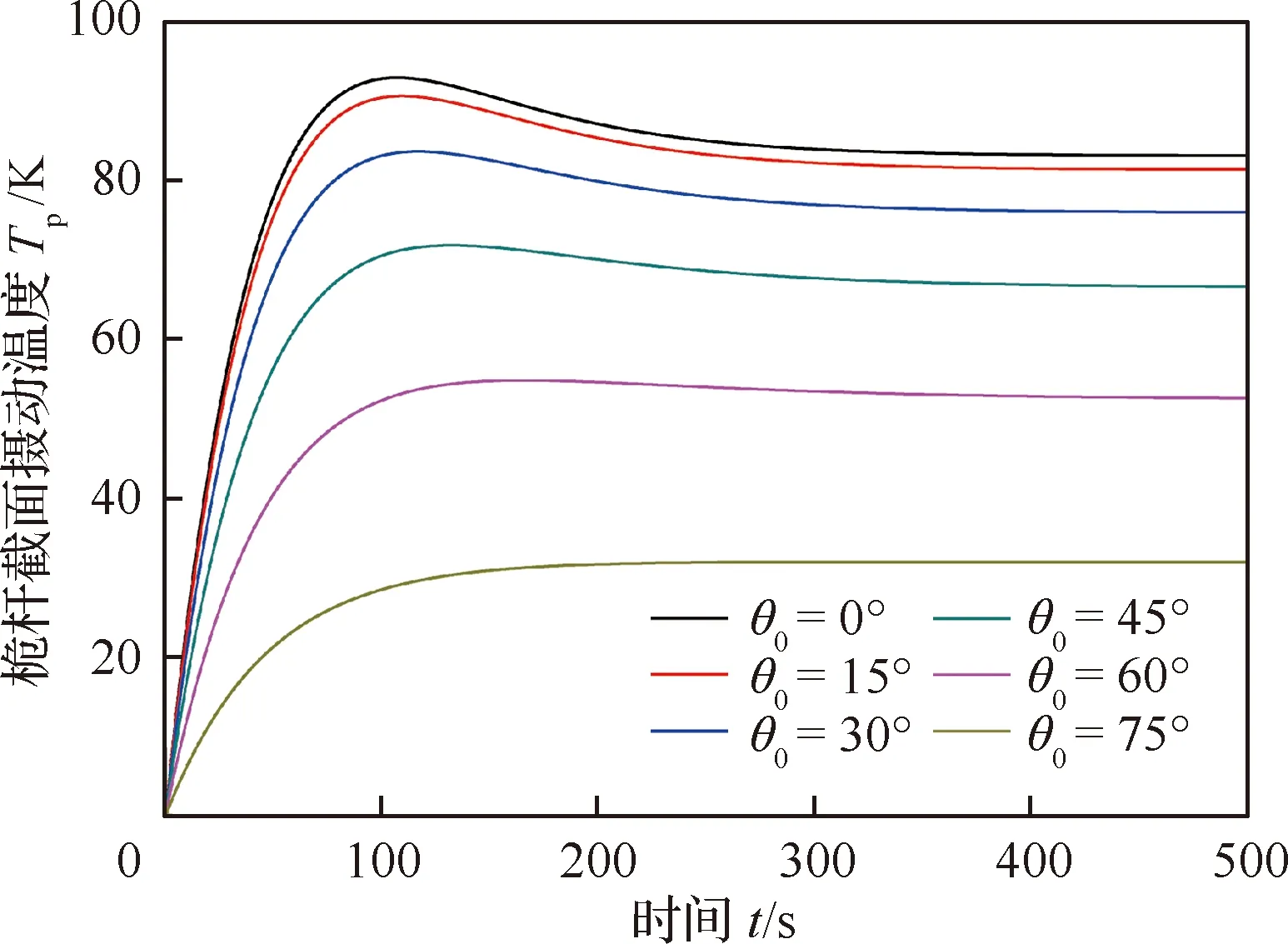
圖11 熱流入射角度對桅桿截面攝動溫度的影響Fig.11 Effect of incident angle of heat flux on perturbation temperature of boom cross-section

如前所述，攝動溫度Tp會對桅桿的熱彎矩造成影響，圖12為不同熱流入射角下，桅桿自由端位移隨時間變化的歷程圖，可以看出熱流入射角的增大造成熱彎矩減小，使得桅桿熱誘發振動的準靜態變形和振幅均有所減小。熱流垂直入射θ0=0°時的太陽帆桅桿熱誘發振動最為劇烈，當熱流入射角θ0=75°時桅桿的熱誘發振動可近似看作靜態的熱致變形。

圖13為桅桿壁厚參數變化時，桅桿自由端位移隨時間變化的歷程圖，隨著桅桿剛度增大，桅桿熱誘發振動的振幅和準靜態變形減小，頻率增大，即太陽帆桅桿剛度的增大有利于抑制熱誘發振動的發生。

提高帆膜預應力可以有效減小帆面的褶皺，提高光壓的反射效率，但是，帆膜預應力也會造成桅桿軸力的變化，從而影響桅桿的熱致振動響應。圖14為帆膜預應力引起桅桿軸力變化時，桅桿自由端位移隨時間變化的歷程圖，其中Pcr為桅桿的一階屈曲載荷值。可知隨著軸力增大，桅桿熱誘發振動的振幅增大，頻率減小。當軸力增大至一定程度，熱誘發振動將會發散，因此，帆膜預應力對于熱誘發振動是不利因素，須適當設計。

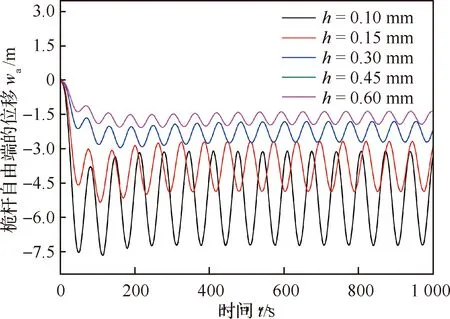
圖13 太陽帆桅桿截面壁厚對熱誘發振動的影響Fig.13 Effect of boom thickness on thermally-induced vibration of solar sail

4 結 論

本文首次建立了太陽帆桅桿-薄膜結構的熱-結構動力學模型，給出了熱-結構耦合動力學方程組的求解流程，分析了太陽帆桅桿-薄膜結構熱誘發振動的特點和影響因素。得到了以下結論：

1) 繞地運行的方形桅桿支撐式太陽帆，由地球陰影進入光照區將會發生明顯的熱誘發振動，振動形式為圍繞準靜態變形的等幅振動。

2) 太陽帆由陰影區進入光照區的姿態角會影響太陽帆結構的熱誘發振動，太陽熱流垂直入射時，桅桿截面的平均溫度和攝動溫度最大，熱誘發振動最劇烈，隨著熱流入射角的增大，桅桿截面攝動溫度減小，熱誘發振動減弱，頻率不變。

3) 隨著桅桿壁厚增加，剛度增大，桅桿熱誘發振動的振幅和準靜態變形減小，頻率增大，桅桿剛度增大有利于抑制太陽帆結構發生熱誘發振動。

4) 帆膜預應力將造成桅桿軸力的變化，影響桅桿的熱致振動響應，隨著桅桿軸力增大，桅桿熱誘發振動的振幅增大，頻率減小。當軸力增大至一定程度，熱誘發振動將會發散。