MEMS慣測技術在管道測繪系統中的應用

楊繼紅，馬 濤，吳亮華，季 陽

(1.海裝駐北京地區某軍事代表室，北京 100074; 2.北京自動化控制設備研究所，北京 100074)

0 引言

管道作為石油、天然氣最經濟合理的運輸方式，具有諸多優點，但油氣管道長期服役后，會因外部干擾、腐蝕、管材和施工質量等原因造成安全隱患。因此，需要借助各種檢測技術，有效地檢測出管道存在的缺陷和變形，并精準確定存在缺陷和變形的位置，為管道的完整性管理和安全評價提供依據，確保管道的安全運行。

隨著慣性技術的不斷發展，采用慣性技術進行測繪已經取得了許多成功的案例[1]，其中，采用慣性測量裝置精確測繪出管道的地理坐標[2-6]，對管道缺陷進行準確定位，是一種十分有效的方法。并且，隨著微機電系統(Micro-Electro-Mechanical System，MEMS)技術的不斷成熟，應用MEMS慣測技術可以對口徑更小的管道進行測繪，擴大了慣性技術對管道測繪的覆蓋范圍。

慣性測量技術中利用載體加速度的二次積分獲得載體位置，因此，獲得積分初始值也是慣性測量裝置在工程應用中的重要環節。一般地，管道慣測裝置的初始位置由外部裝訂，初始速度為0，而初始姿態值需要由慣測裝置初始對準得到[7]。

由于MEMS慣性器件的測量精度通常較低，MEMS陀螺敏感的地球角速度湮沒在陀螺噪聲中，無法進行自對準。因此，MEMS慣測裝置在使用中經常利用外部信息為其提供方位初始信息，如磁羅盤、雙天線衛星接收機等。但由于管道測繪的具體應用條件，難以采用這些設備提供初始方位，造成MEMS慣測裝置在管道測繪中使用不便。

本文利用地標點信息，直接為MEMS慣測裝置裝訂方位信息，并利用里程計信息作為觀測量，采用因子圖原理和和積算法進行組合導航，利用到達路標點的信息修正初始方位。初始方位修正后，再次進行組合導航，并進行平滑計算，實現管道中心線的精確測量，測量現場無需使用其他配套設備，也無需額外操作，有利于MEMS慣測裝置在管道測繪中的應用推廣。

1 系統模型

1.1 坐標系定義

n：導航坐標系oxnynzn，東北天地理坐標系，xn軸指向東，yn軸指向北，zn軸指向天；

b：慣測裝置載體坐標系oxbybzb，右前上坐標系，xb軸指向慣測裝置的右側，yb軸指向慣測裝置的前向，zb軸指向慣測裝置的上方；

m：里程計載體坐標系oxmymzm，右前上坐標系，ym軸指向里程計測量軸的前向，xm軸與ym軸垂直指向右側，zm軸與oxmym面垂直指向上；

i：慣性坐標系oxiyizi，與b系初始時刻指向相同；

e：地球坐標系oxeyeze，oxeye平行于赤道平面，xe軸指本初子午線方向，ze軸指向北極，ye軸與其他兩軸組成右手系。

1.2 慣性導航誤差模型

本文直接給出慣性導航誤差模型如下[8-11]

(1)

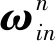
1.3 系統狀態模型

選取系統的狀態變量為

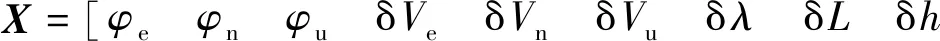
其中，βx和βy分別為里程計對應軸向的安裝誤差，δK為里程計標度因數誤差。

假設慣性器件誤差為零偏誤差與白噪聲之和，零偏誤差為隨機常值；假設里程計安裝誤差殘差及標度因數誤差在系統運行中基本保持不變，則

(2)

根據式(1)、式(2)可得系統的狀態方程為

(3)

其中：F為系統狀態矩陣，W為系統噪聲，分別由陀螺測量噪聲和加速度級測量噪聲組成。

1.4 系統觀測模型

里程計輸出信息為位移增量，可在一定時間內對其進行累積[12-15]，并且與同時間內的慣性導航位移做差，得到系統的觀測變量，即

(4)

根據式(4)得系統的觀測方程為

Z=HX+V

(5)

其中：H為觀測矩陣，V為觀測噪聲，ΔS為里程計輸出累積的位移變化量。則觀測矩陣為

(6)

2 基于因子圖的遞推估計算法

因子圖是一種用來描述如何將多變量的全局函數分解成多個局部函數乘積形式的雙向圖[16]，由變量節點、函數節點和邊線組成。因子圖的邊線是指變量節點和函數節點的連線，當且僅當該變量是函數的自變量時，對應的變量節點才與對應的函數節點用邊線連接。

將式(3)、式(5)表示的線性系統進行離散化，可得

(7)

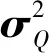
式(7)表示的系統為一階馬爾科夫系統，畫出其因子圖如圖1所示，其中白色圓圈表示標量節點，黑色方框表示函數節點。

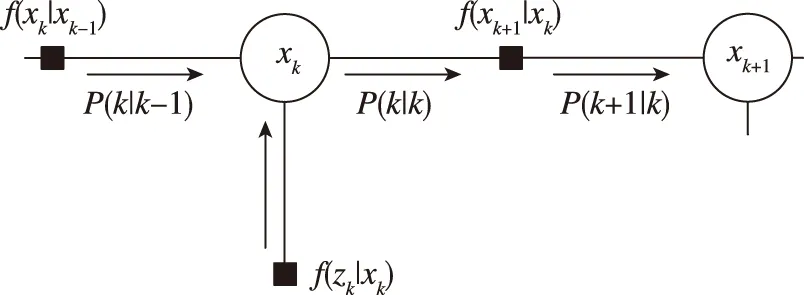
圖1 組合導航系統的因子圖Fig.1 The factor graph of integrated navigation system measurement

根據因子圖的和積算法[17]，由變量節點傳遞給函數節點的消息表示為

μx→f(x)=∏h∈n(x){f}μf→x(x)

(8)

由函數節點傳遞給變量節點的消息表示為

μf→x(x)=∑～{x}(f(X)∏z∈n(f){x}μz→f(z))

(9)

根據圖1所示的系統因子圖，將系統(7)寫成條件概率密度函數的形式，可以表示為

f(x1,…,xk|z1,…,zk)=

(10)

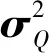
將變量節點傳遞給函數節點的消息表示為P(k|k)，將函數節點傳遞給變量節點的消息表示為P(k+1|k)，則根據圖1和式(8)、式(9)可得

P(k|k)=f(xk|z1,…,zk)

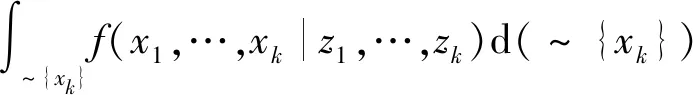
=P(k|k-1)f(zk|xk)

(11)

(12)

根據式(11)和式(12)，即可實現對系統狀態變量的遞推估計。

3 試驗結果

為了驗證MEMS慣測技術在管道測繪系統中的應用效果，進行了管道牽引試驗，試驗設備連接如圖2所示。試驗管道長度約103.8m，牽引速度約為1m/s，共試驗3次，第2次和第3次試驗在管道中部約50.5m處，較第1次試驗分別沉降20cm和41.5cm，共采集3個條次數據，管道中心線測繪結果如圖3～圖5所示。

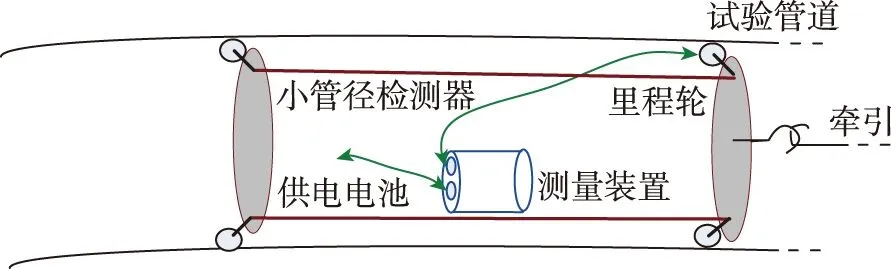
圖2 牽引試驗設備連接示意圖Fig.2 Schematics of device linking in dragging tests

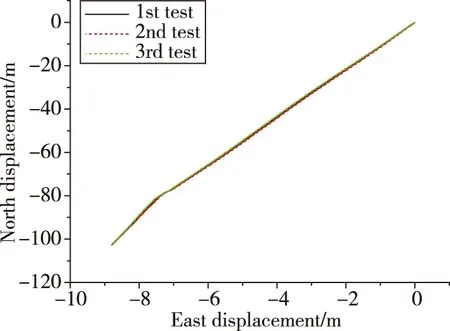
圖3 牽引測試水平位移結果Fig.3 Horizontal displacement in dragging tests

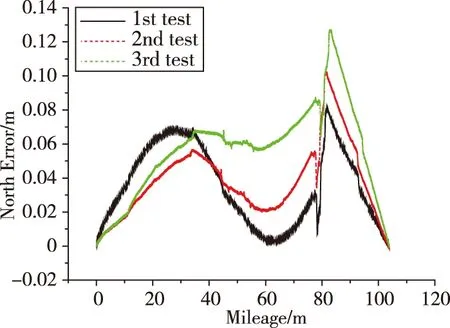
圖4 牽引測試北向誤差結果Fig.4 North displacement error in dragging tests

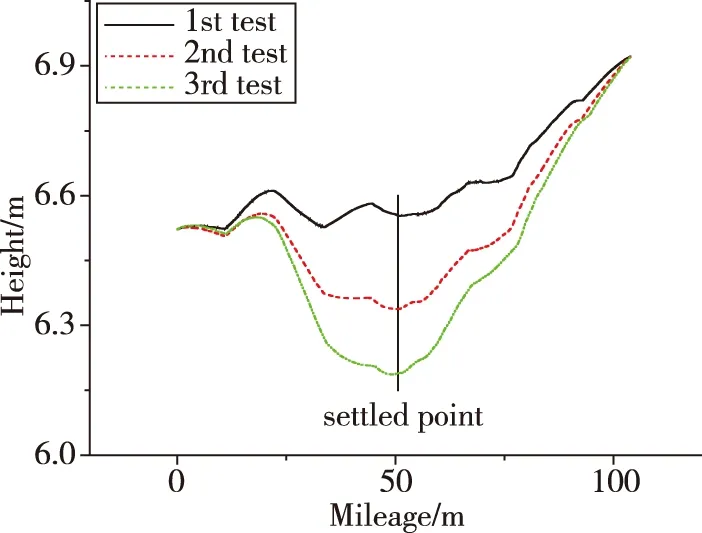
圖5 牽引測試高度結果Fig.5 Height in dragging tests

由于測試沒有絕對基準，需要通過3次測量的重復性來說明測量結果精度，所以將3次試驗的同項結果在同一曲線圖中呈現。圖3和圖4分別為3次試驗的水平位置測量結果和高度測量結果，可以看出，3次測試的水平位移基本相同，但由于每次試驗的時間長度略有不同，無法通過直接相減觀察位移測量結果的重復性。因為實際管道在北向位移隨里程基本呈線性變化，所以利用各次試驗的北向位移結果直接與隨里程線性的直線相減作為北向位移測量誤差，結果見圖4。可以看出，各次試驗的北向位移基本相同，最大相差點在管道中部沉降點之后，為第1次試驗和第3次試驗的差值，約為5cm。圖5為高度測量結果，可以看出測量結果基本體現了試驗中的沉降過程，在沉降點的測量結果分別為6.55m、6.33m和6.18m，最大偏差同樣在5cm以內。

4 結論

針對MEMS慣測技術在管道測繪系統中的應用，本文進行了如下研究：

1)建立了慣測裝置在管道測繪應用中的系統模型，畫出了模型的因子圖，并在此基礎上給出了和積算法應用與該模型的遞推算法。

2)利用地標點信息，直接為MEMS慣測裝置裝訂初始方位信息，在迭代計算的過程中，不斷修正方位誤差，利用到達路標點的信息修正初始方位。試驗表明該方法有效，直接裝訂導致的初始方位誤差不會影響最終測繪結果。

3)利用MEMS慣測裝置進行了管道牽引試驗，采用因子圖及和積算法對試驗數據進行了處理，處理結果顯示在100m間隔的路標點條件下，單向定位精度能夠達到5cm，證明了算法的適用性。