基于約束總體最小二乘的泰勒級數定位算法

陸劍鋒 謝勝東

1(泰州職業技術學院信息技術學院 江蘇 泰州 225300)2(南京信息工程大學計算機與軟件學院 江蘇 南京 210044)

0 引 言

無線定位是指利用無線信號的物理參數估計目標節點在某一坐標系統中的位置，最初是為了滿足航海導航以及精確制導等方面要求，其典型代表為20世紀70年代的全球定位系統(GPS)。自1996年美國聯邦通信委員會要求無線蜂窩系統必須能夠對發出緊急呼叫的移動用戶實現準確定位后，無線定位便引起了眾多學者的廣泛關注[1]。目前，無線定位除了應用于蜂窩網絡中的緊急呼叫外，還可以用于智能交通、數字城市以及現代化農業、醫療等領域中，以實現目標跟蹤、資源調度和導航等為目的，因此具有廣泛的應用范圍。

根據物理量的不同，現有定位算法可以分為基于信號強度(Received Signal Strength，RSS)的定位[2]、基于信號到達時間(Time of Arrival，TOA)的定位[3]、基于信號到達時間差(Time Difference of Arrival，TDOA)的定位[4]以及基于信號到達角度(Angle of Arrival，AOA)的定位[5]四種基本類型。由于RSS定位精度低、AOA實現復雜以及TOA需要目標節點與源節點之間時間同步[6]，在無線定位系統中，現階段使用最為廣泛的就是TDOA算法。例如，在GSM和LTE系統中，均采用該類算法進行位置估計。

目前關于如何提高TDOA算法定位精度的研究主要可以分為三大類：(1) 最小二乘類定位算法。這類算法基于目標節點到達不同錨節點距離平方之差的誤差2-范數最小原則，將位置估計描述為一個空間的向量仿射變換問題，基于普通最小二乘(Least Square，LS)準則，使用拉格朗日算子法[7]、廣義信任域法[8]或半正定規劃法[9]即可求得該準則下的全局最優解。然而，使用LS準則求解原問題本身就是存在偏差[10]，因此，上述全局最優解未必是原問題的全局最優解。(2) 凸規劃類定位算法[11]。這類算法基于目標節點到達不同錨節點距離之差的誤差2-范數最小原則，將估計量的最優值表示成求解一個非凸非線性函數的最小值問題，進而通過松弛技術，將原問題轉化成一個非線性凸函數最小化問題，以該問題的最優解作為目標節點坐標的最優估計值。然而，原問題與轉換后的問題之間并不等價，因此，轉換后問題的最優值未必是原問題的最優值。(3) 泰勒級數類定位算法[12]。與第二類算法的準則相同，這類算法也是基于目標節點到達不同錨節點距離之差的誤差2-范數最小原則，將估計量的最優值描述成求解一個非線性最小二乘函數的最小值問題，進而使用泰勒級數展開法，將到達時間差函數用某個初始坐標點的一階泰勒級數近似，實現了非線性最小二乘函數到線性最小二乘函數的轉變。在獲得修正步長的最小二乘解后，更新原初始坐標點。如此不斷迭代，從而逐漸逼近真實坐標點。由于忽略了泰勒級數的高次項，因此迭代解未必是原始非線性最小二乘問題的最優解。很顯然，上述三類算法均無法獲得各自所對應的原始問題的全局最優解。

本文主要研究第三類，即泰勒級數類定位算法。對于該類算法，初始坐標點的選擇是一個重要環節，它直接決定了此類算法的性能。現有算法中，常見的初始點選擇方法主要包括最小二乘法[4]、最速下降法[13]、殘差加權法[14]以及二階錐松弛法[15]等。事實上，幾乎所有最小二乘類和凸規劃類定位算法所獲得的位置估計值均可以作為泰勒級數類算法的初始坐標點，區別主要在于算法的收斂性、迭代次數以及估計精度的不同。當初始坐標點與實際位置值越接近時，算法的收斂性越能得到保障，迭代次數也將越少，定位精度也將越高。

1 定位模型

考慮到二維坐標系統中的定位算法經簡單擴展后便可適用于三維坐標系統，因此本文以二維坐標系統為研究環境。假設在二維坐標系統中，存在某個位置未知的目標節點，其坐標記為(x,y)，同時還存在N個不在同一條直線上位置已知的普通錨節點，它們的坐標分別記為(xi,yi),i=1,2，…,N，以及一個位于坐標系統原點的參考錨節點。

我們可以使用時延估計法[16]獲得電磁波或聲波從目標節點到達普通錨節點i與參考錨節點之間的時間差ti0，然后乘以它們的傳播速度，即可獲得目標節點到達兩節點之間的距離差di0。由此可見，TDOA定位算法可以看成是基于距離差的定位算法。因此，在本文中，我們將以距離差來代替時間差。

目標節點到達普通錨節點i與參考錨節點距離差的真實值fi0(x,y)可分別表示為：

(1)

i=1,2，…,N

由于我們事先并不知道目標節點的坐標值，因此不能通過式(1)來計算距離差，而只能通過測量得到距離差di0的值：

di0=fi0(x,y)+ni0i=1,2,…,N

(2)

式中：ni0為測量誤差，我們假設它們之間獨立同分布。

1.4.3 煙葉常規化學成分 分析烤后煙葉樣品的常規化學成分，包括總氮、煙堿、總糖、還原糖、鉀、氯，并計算糖堿比、氮堿比和鉀氯比。具體參照文獻[17]的方法進行。

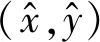
(3)

式(3)是求解一個非線性最小二乘函數的最小值問題，這類問題因存在多個極值點，故一般不存在或難以求得其全局最優解，而只能通過某種優化算法，如牛頓法、最速下降法等方法獲得它的局部最優解。

2 定位算法

如果能夠求得式(3)的全局最優解，那么該解即可作為節點的位置坐標最優估計值，但如前所述，函數的非凸性使其成為一件較為困難的事情，牛頓法、最速下降法等搜索算法只能獲得函數的局部最優解。如果我們可以對非凸函數進行線性近似，那么就能獲得近似后函數的全局最優解，盡管其未必是原函數的全局最優解，但其性能可能會優于原函數的局部最優解。一方面，泰勒級數分解使得這種線性近似成為可能，另一方面，CTLS算法利用了牛頓法獲得了SDR模型中的局部最優解。因此，我們將這兩種方法結合，提出一種基于完全約束最小二乘的泰勒級數定位算法(CTLS-Taylor)，以期望能夠獲得更好的定位效果。CTLS-Taylor包含兩個方面的內容：(1) 泰勒級數的線性近似原理；(2) 利用CTLS算法進行目標節點位置坐標初始點的選擇。

2.1 泰勒級數線性近似原理

(4)

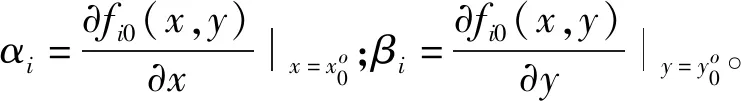
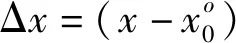
(5)

式(5)等價于求解如下線性方程式在普通最小二乘準則下的最優解：

AX=b

(6)

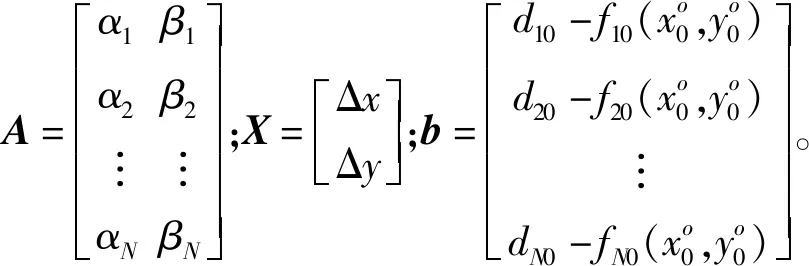
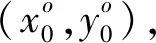
2.2 初始點的選擇

很顯然，初始點越接近式(3)的最優解，則不僅能夠保證迭代過程的收斂，而且能夠減少迭代的次數，提高位置估計的速度。考慮到最小二乘類定位算法中的CTLS算法[10]能夠獲得較高的位置估計精度，本文采用CTLS算法來獲取目標節點的初始位置。

基于目標節點到達普通錨節點與參考錨節點的距離平方值之差的誤差平方和最小原則，目標節點的坐標可以通過下式進行描述：

Aθ=b

(7)

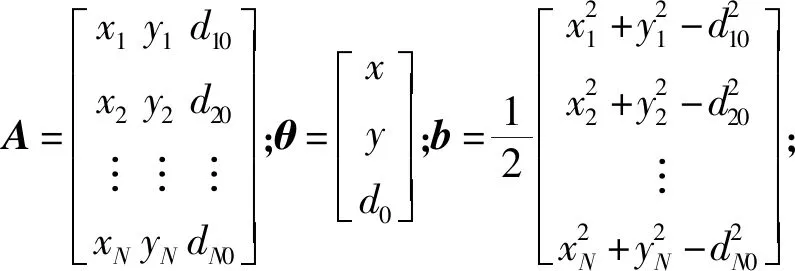
對于式(7)，我們可以求得它在普通最小二乘準則下的最優值[7]。但該準則是建立在矩陣A中所有元素均不存在誤差的基礎上，而事實上，A中最后一列的所有元素均為測量所得，必然存在著測量誤差，因此采用普通最小二乘準則獲得的最優值顯然是不準確的。此時，可以采用總體最小二乘準則[17]，它不僅考慮了向量b中的誤差，同樣考慮到了矩陣A中元素的誤差，其目的是在最小化所有誤差平方和的情況下，使得式(7)有唯一確定解。于是在該準則下，式(7)的最優值θ等價于式(8)的最優解：

s.t.Aθ-b=Gn

(8)

式中：

利用牛頓迭代法，我們可以很容易地求得式(8)的一個局部最優解θ，并將其中的x和y作為目標節點位置坐標的粗估計值。

2.3 CTLS-Taylor算法

這里，我們給出CTLS-Taylor算法的完整過程：

3 仿真分析

本文的仿真環境為MATLAB 7.0，仿真參數來自文獻[18]：在一個100 m×100 m的2維坐標系統中，存在一個實際坐標(42,12) m的目標節點，同時存在9個普通錨節點，它們的坐標依次為(16,42) m、(34,52) m、(58,30) m、(78,18) m、(66,48) m、(30,-12) m、(22,12) m、(57,-3) m、(12,-28)m，另外還存在一個參考錨節點，其坐標為(0,0) m。TDOA的測量噪聲服從均值為0，方差為δ2的高斯分布。為了評價CTLS-Taylor算法的性能，將其與CTLS算法、QCLS算法以及QCLS-Taylor算法[4]進行比較，并從定位誤差和泰勒級數迭代次數兩個角度進行衡量。本文中定位誤差e的計算公式為：

(9)

式中：N為仿真次數。

圖1和圖2為普通錨節點數目分別為5個和9個時，不同算法的定位誤差。可以看出：(1) 隨著測量噪聲方差的增加以及普通錨節點數目的增多，泰勒級數類算法的定位誤差要優于非泰勒級數類算法，這表明使用泰勒級數法有助于提高定位精度。(2) 本文的CTLS-Taylor算法與QCLS-Taylor算法的定位誤差幾乎相等，不受測量噪聲與普通錨節點數目的影響。這意味著單純從定位誤差的角度看，本文算法與QCLS-Taylor算法的性能相當。(3) CTLS算法的定位誤差要優于QCLS算法，這是因為CTLS算法是基于總體最小二乘準則，而QCLS算法是基于普通最小二乘準則的原因。

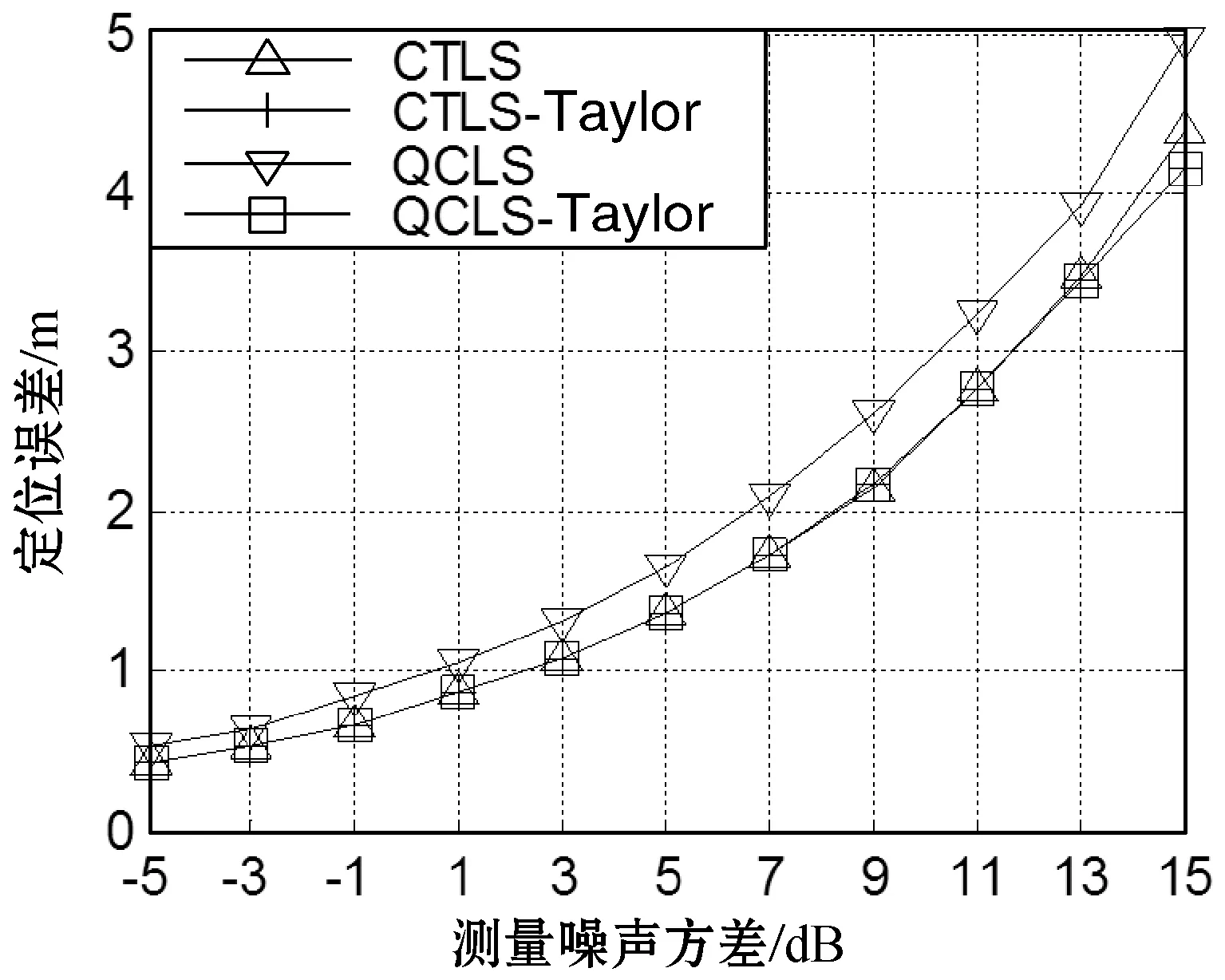
圖1 普通錨節點數目5個的定位誤差

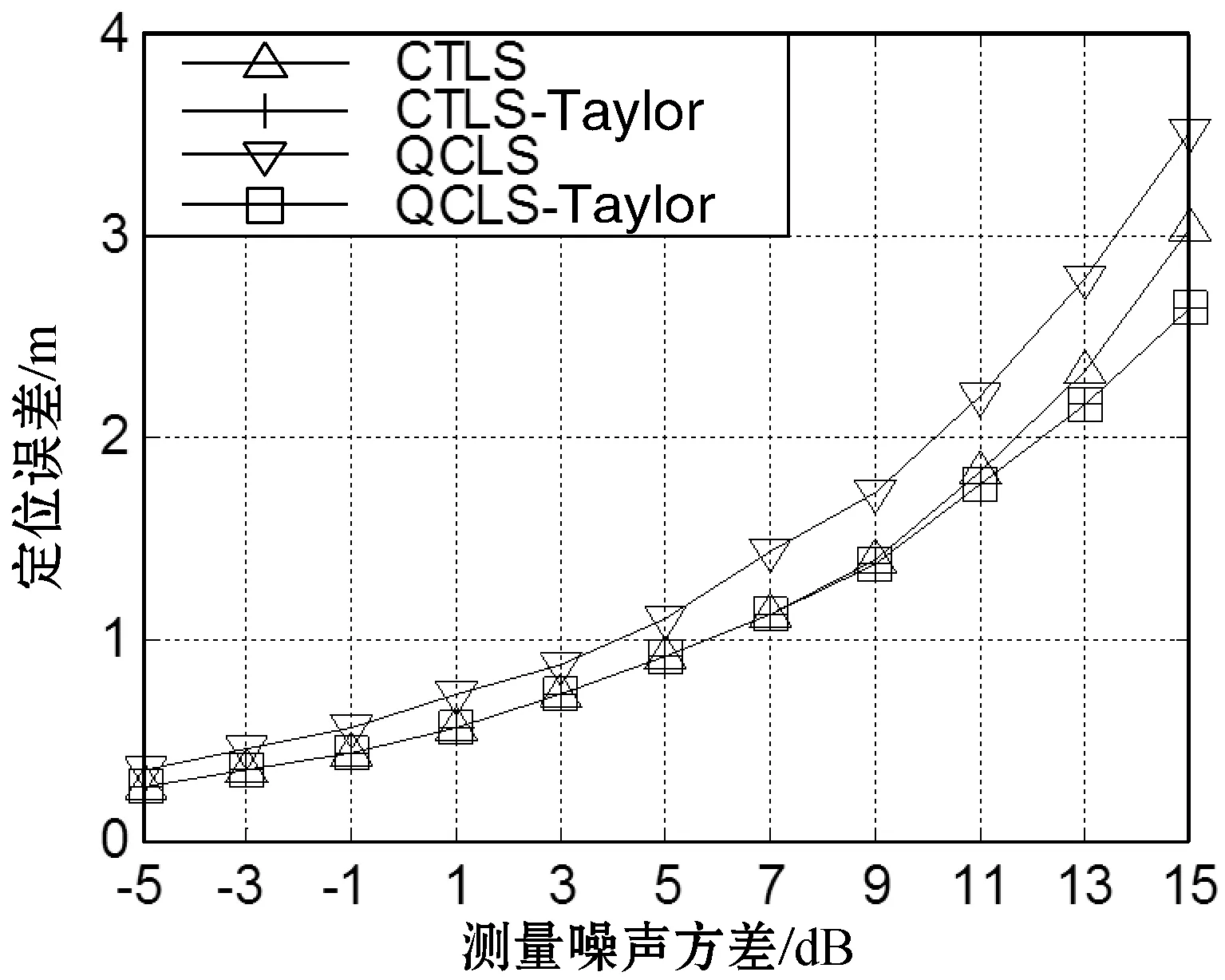
圖2 普通錨節點數目9個的定位誤差

圖3與圖4為普通錨節點數目分別為5個和9個時，兩種泰勒級數類算法所需要的迭代次數。可以看出：(1) 當測量方差較低時，尤其是當信噪比低于-1 dB時，CTLS-Taylor算法幾乎只要迭代一次即可，且與普通錨節點的數目無關，而QCLS-Taylor算法的平均迭代次數均大于1.5次，這與CTLS-Taylor算法的初始點更為接近真實坐標點有關。(2) 當測量方差逐漸增大時，兩個泰勒級數算法的迭代次數均出現不同程度的增加，但CTLS-Taylor算法的迭代次數始終小于QCLS-Taylor算法。

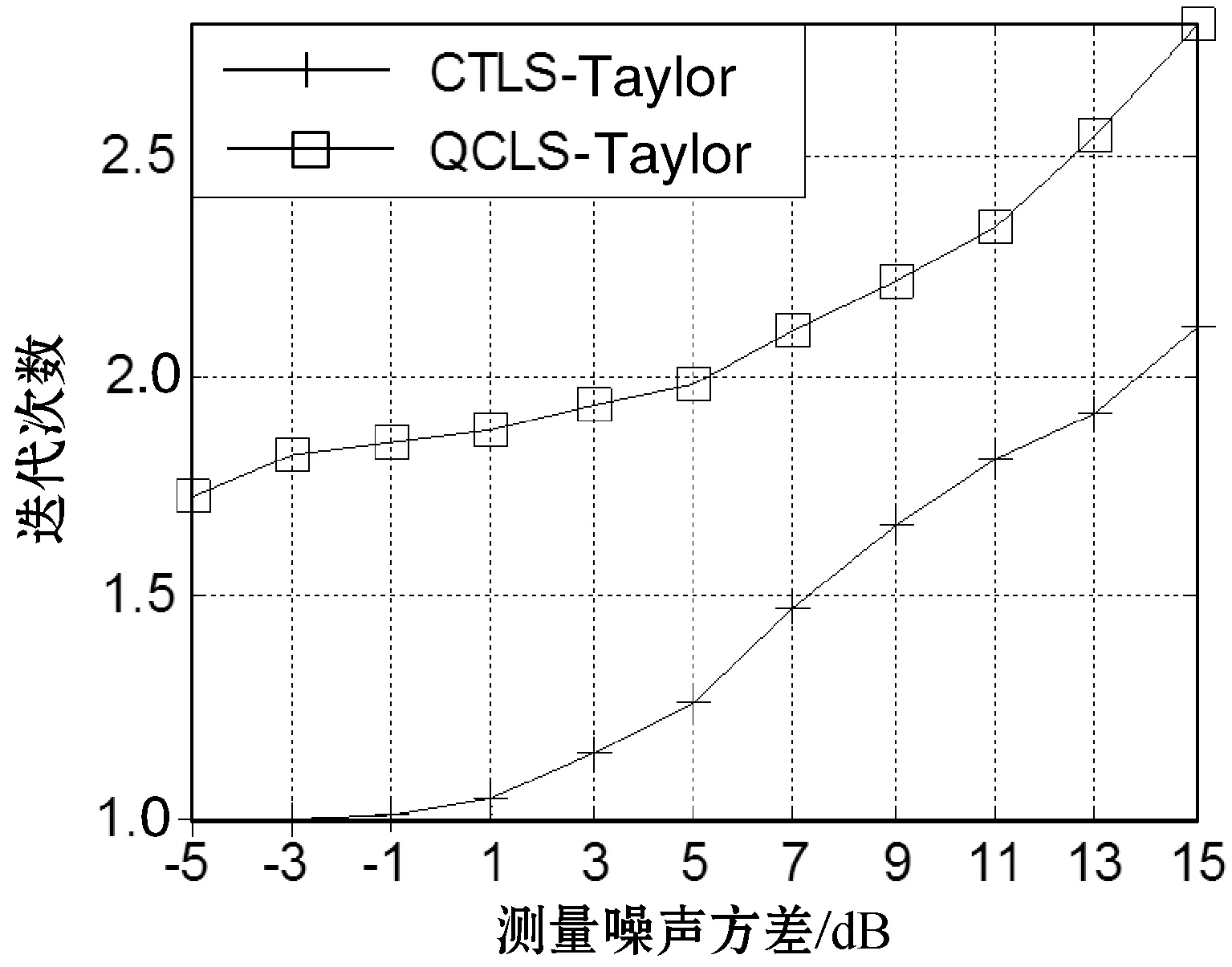
圖3 普通錨節點數目5個的迭代次數

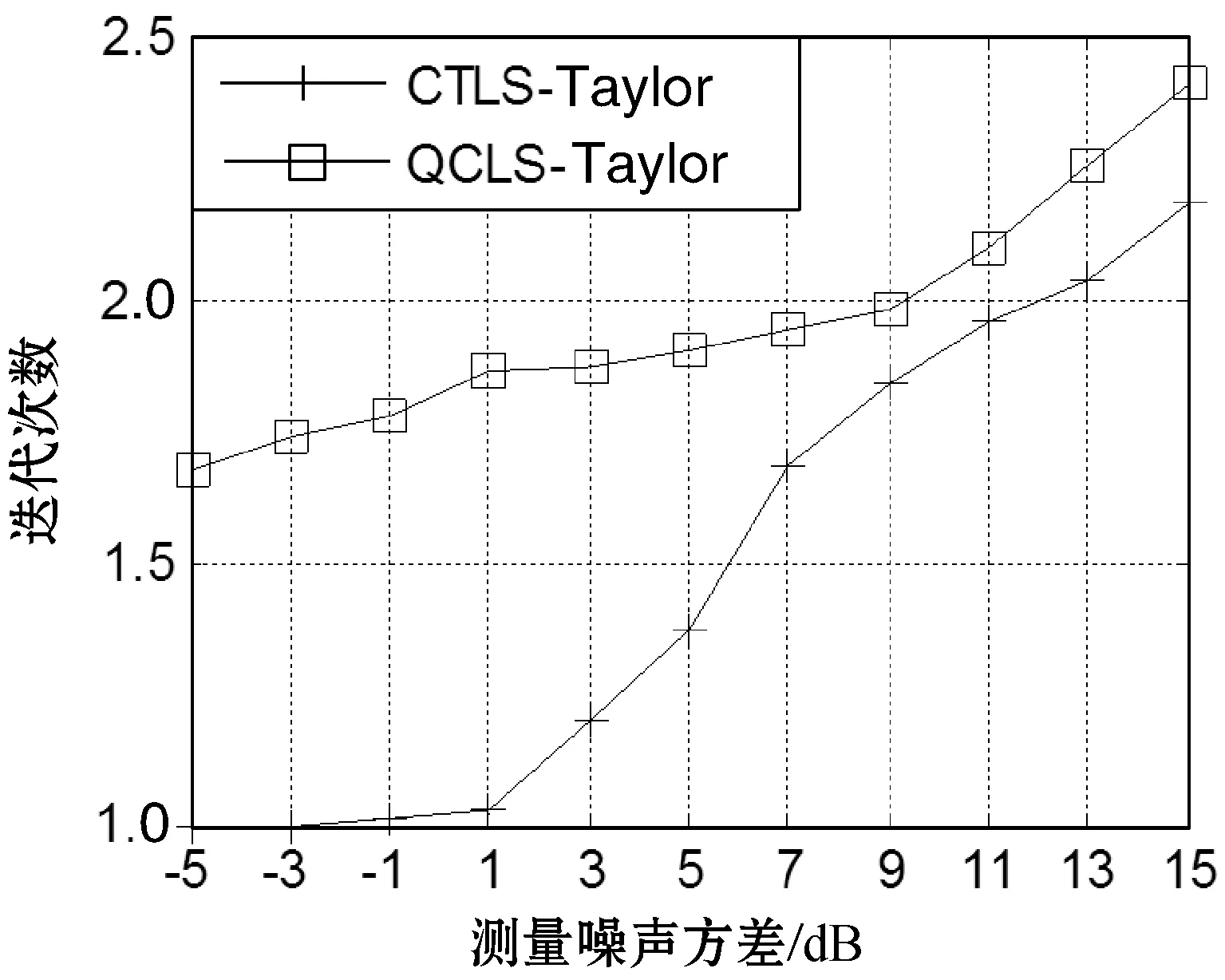
圖4 普通錨節點數目9個的迭代次數

上述結果表明，盡管從定位誤差的角度看，CTLS-Taylor算法的性能與QCLS-Taylor算法相當，但前者的迭代次數卻小于后者，也就意味著前者的定位速度優于后者。

4 結 語

本文將泰勒級數法與CTLS算法相結合，提出了一種基于約束總體最小二乘的泰勒級數定位算法。該算法利用CTLS方法獲得目標節點坐標位置的粗估計值，并將該值作為泰勒級數展開法的初始點，通過迭代，從而獲得目標節點位置坐標的精估計值。仿真結果表明，CTLS-Taylor算法不僅能夠獲得與QCLS-Taylor算法相同的定位精度，而且迭代次數有了明顯減少；同時與CTLS算法相比，當測量噪聲較高時，CTLS-Taylor算法的定位精度更高。