含裂紋容器的有限元分析

韋權權 王政威 楊溪榮 羅惠敏

摘 ?????要：利用有限元通用軟件ANSYS Workbench，建立容器的有限彈性體三維有限元模型，進行地震工況下不同裂紋長度、不同裂紋方向、不同支腿數量和不同容器高度下的應力分析，得到斷裂力學中表征裂紋尖端附近應力場，進而得出以下結論：裂紋長軸長度和角度的變化對應力場影響;等效應力值隨著裂紋長軸長度的變大顯著變大，等效應力最大點隨著裂紋長軸長度的變大由長軸邊緣移到短軸邊緣;等效應力值隨著裂紋長軸角度的變大而變化，在22.5°時達到最大;等效應力最大點隨著裂紋長軸角度的變大，由長軸邊緣移到短軸邊緣。

關 ?鍵 ?詞：裂紋;有限元;容器;分析

中圖分類號：TQ 052 ??????文獻標識碼： A ??????文章編號： 1671-0460（2019）08-1885-04

Abstract： Using ANSYS Workbench， a finite elastomer three-dimensional finite element model of the container was established. Stress analysis under different crack lengths， different crack directions， different number of legs and different height of the container was carried out under seismic conditions. The stress field near the crack tip was characterized in fracture mechanics， and the following conclusions were drawn： the change of the length and angle of the long axis of the crack affects the stress field; the equivalent stress value increases significantly with the increasing of the length of the long axis of the crack， and the maximum point of the equivalent stress moves from the edge of the long axis to the edge of the short axis with the increasing of the length of the long axis of the crack; the equivalent stress value changes with the increasing of the angle of the long axis of the crack， reaching its maximum at 22.5 degrees; the maximum point of equivalent stress moves from the edge of the long axis to the edge of the short axis with the increasing of the angle of the long axis of the crack.Key words： Crack; Finite element; Vessel; Analysis

在對煉油和化工裝置的運行與定期檢驗中，常會發現部分容器存在裂紋缺陷。如果一旦發現容器的裂紋缺陷就立即停產檢修或者報廢處理，那么會存在不合理和不經濟性。尤其是在儲存大量危險介質的含裂紋儲罐，其危險性大、波及面廣;若其存在裂紋缺陷，我們如果能對缺陷的發展及可能造成的危險做出判斷，那么我們就可以最大限度的發揮儲罐的經濟效益而不會發生危險。因此，工程界一直在努力尋找這種安全評定的準則。

在工程應用中，由于容器的實際結構通常都是有限彈性的，因此研究有限彈性的表面裂紋結構與實際相符更有研究意義。對于有限彈性體三維表面裂紋問題，目前國內外學者大都通過數值分析方法求出的。鑒于前人的經驗本文采用有限彈性體計算應力強度因子。

1 ?有限元模型建立

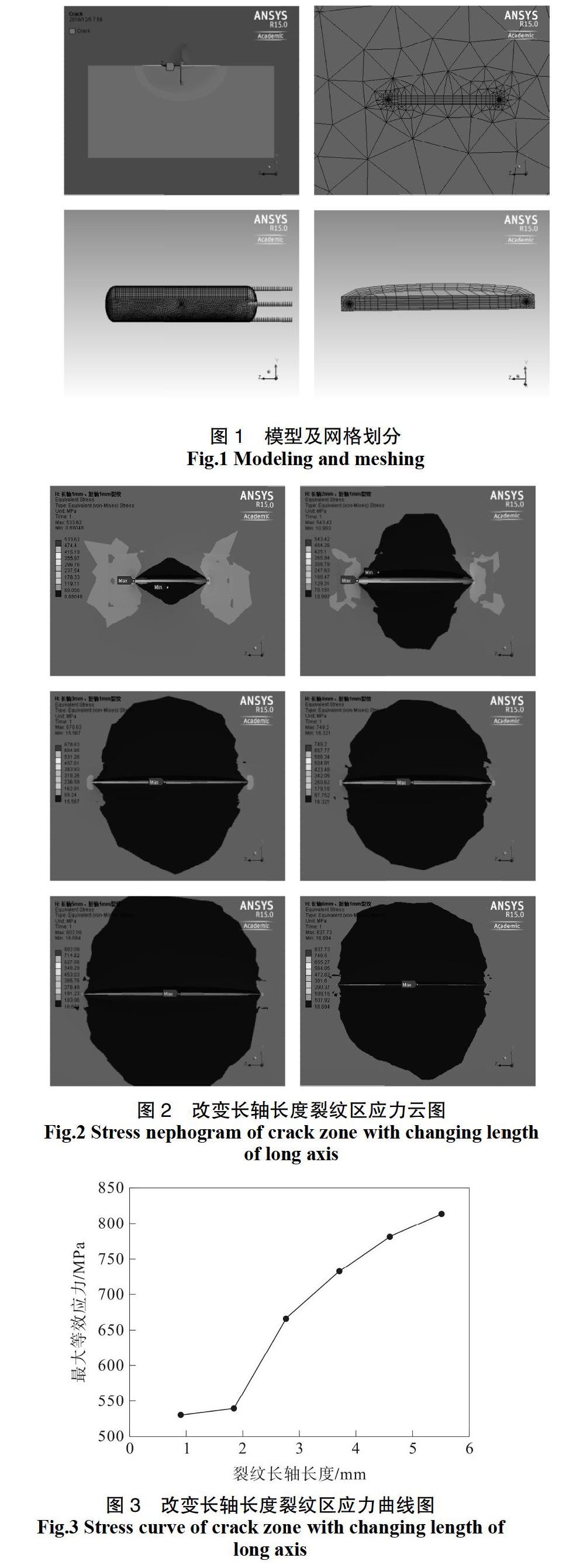
考慮到本文主要考察裂紋，所以建模時忽略接管和部分小結構。由于考慮的裂紋位于儲罐筒體中部，忽略其他結構不會影響裂紋的考察。殼體采用實體單元建模，支腿采用梁單元建模，梁單元與實體單元之間采用MPC綁定。

本儲罐結構及載荷形式復雜，所以本文選取全模型進行計算模擬。本文采用大型通用有限元軟件ANSYS WORKBENCH自帶的建模工具DesignModeler建立三維實體模型，為了模擬裂紋應力場、應變場以及應力強度因子，在建模時裂紋前沿采用退化的二十節點等參元，其他部位采用二十節點等參元，這樣既能求出裂紋前沿的應力奇異場又能滿足很好的精度[1-5]。

由于本文分析儲罐結構的全模型，因此在其內壁處施加壓力載荷，在整體上施加地震載荷，在支腿底部施加全約束。由于本文裂紋處載荷工況的復雜性，在其裂紋處將產生復合型裂紋形式。在裂紋的建模過程中，建立橢圓形表面裂紋，為控制裂紋處的網格密度，本文在網格裂紋處沿裂紋寬度方向劃分8條輪廓網格，以便為后續考察8條輪廓路徑上的應力強度因子做準備。模型及網格劃分見圖1。

2 ?含裂紋容器的應力分析

2.1 ?裂紋長軸尺寸對應力場的影響

為了進一步分析軸向裂紋長軸（裂紋長軸方向垂直于儲罐筒體環向應力方向）方向尺寸變化（裂紋短軸尺寸不變）對有限彈性體中表面裂紋應力場的影響及其規律性，我們選取裂紋短軸直徑為1 mm，長軸直徑分別為1、2、3、4、5、6 mm的6種橢圓表面裂紋形式進行分析。

由圖2可以看出隨著裂紋長軸長度的變大，等效應力值也顯著變大，等效應力最大點的位置隨著裂紋長軸長度的變大，由長軸邊緣移到短軸邊緣。由此說明，當裂紋長軸長度較短時，其主要沿裂紋長軸方向擴展;當裂紋長軸長度較長時，其主要沿裂紋短軸方向擴展。

由圖3可以看出裂紋長軸長度小于2 mm時，等效應力增長緩慢;裂紋長軸長度在2～4 mm時，等效應力值增長迅速;當裂紋長軸長度大于4 mm后，等效應力增長又變緩慢。

2.2 ?裂紋長軸角度對應力場的影響

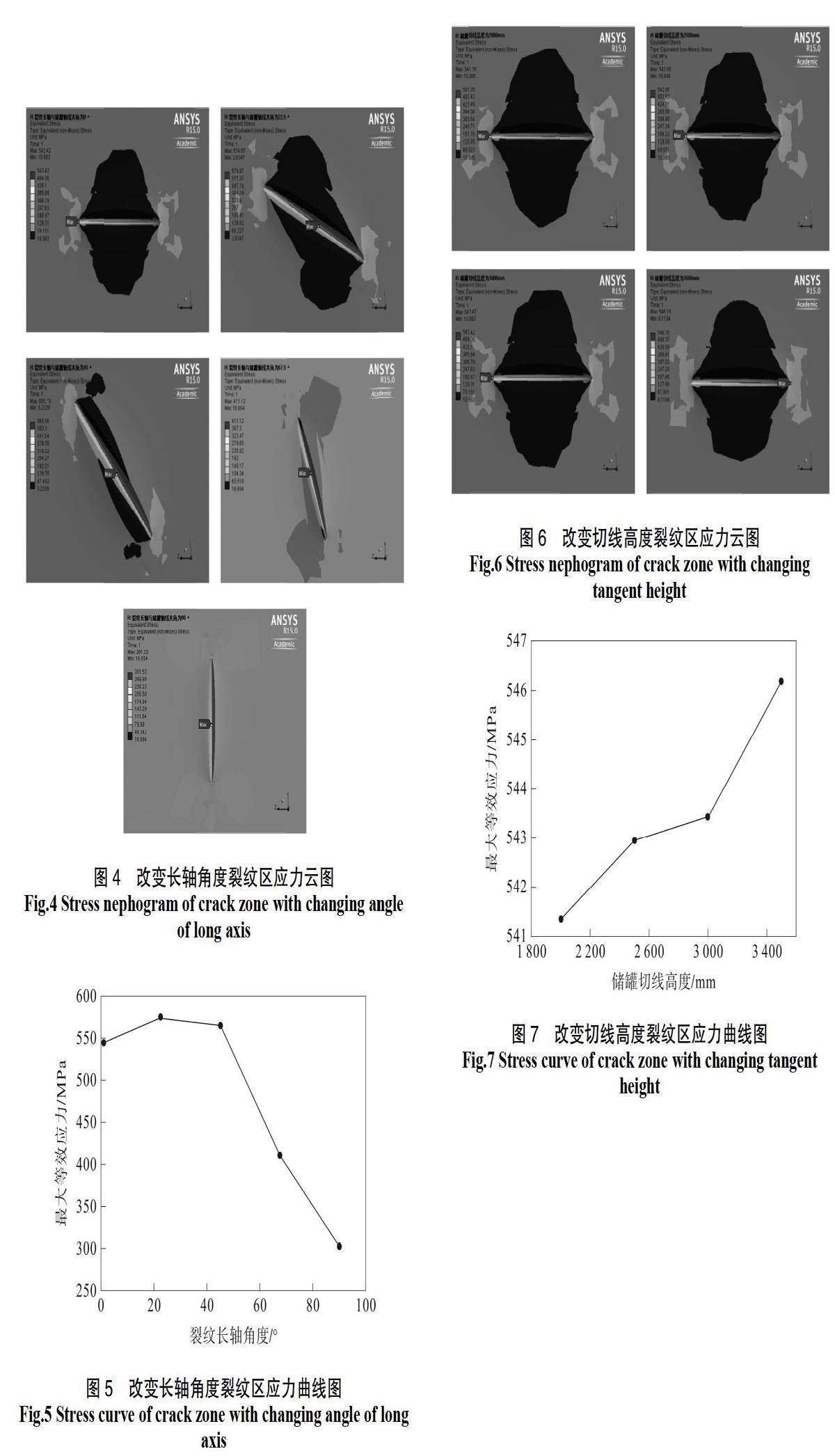
為了進一步分析軸向裂紋長軸（裂紋長軸方向垂直于儲罐筒體環向應力方向）方向角度變化（裂紋長軸直徑2 mm、短軸直徑1 mm）對有限彈性體中表面裂紋應力場的影響及其規律性，我們選取裂紋長軸與儲罐軸線夾角分別為0°、22.5°、45°、67.5°、90°的五種橢圓表面裂紋形式進行分析。

由圖4可以看出隨著裂紋長軸角度的變大，等效應力最大點隨著裂紋長軸角度的變大，由長軸邊緣位置移到裂紋短軸邊緣位置。由此說明，當裂紋長軸角度較小時，其主要沿長軸方向擴展，當裂紋長軸角度較大時，其主要沿短軸方向擴展。

由圖5可以，看出裂紋長軸角度小于22.5°時，等效應力緩慢增長;裂紋長軸角度大于22.5°時，等效應力值下降;在22.5°～45°之間，等效應力值緩慢下降;超過45°時，等效應值迅速下降。此種現象是因為裂紋張開方向受力由環向應力逐漸變為軸向應力，張開方向應力值逐漸變小導致的。

2.3 ?切線高度對裂紋應力場的影響

為了進一步分析儲罐切線高度對有限彈性體中表面裂紋（裂紋長軸直徑2 mm、短軸直徑1 mm）應力場的影響及其規律性，我們選取儲罐切線高度分別為2 000、2 500、3 000、3 500 mm四種儲罐中心位置橢圓表面裂紋形式進行分析。

由圖6、圖7可以看出隨著儲罐切線高度的變大，等效應力最大值隨著儲罐切線高度的增加而緩慢增加，等效應力最大點的位置不變。由此說明，儲罐切線高度的增大，其由于承受地震載荷產生的彎矩作用而使軸向應力增大，從而影響裂紋等效應力最大值。

2.4 ?支腿數量對裂紋應力場的影響

為了進一步分析儲罐支腿數量對有限彈性體中表面裂紋（裂紋長軸直徑2 mm、短軸直徑1 mm）應力場的影響及其規律性，我們選取儲罐支腿數量分別為3、4的兩種儲罐中心位置橢圓表面裂紋形式進行分析。

由圖8可以看出隨著儲罐支腿數量的增多，等效應力最大值基本沒有變化，等效應力最大點的位置不變。由此說明，儲罐支腿數量的多少，對于其遠離支腿部位的局部應力沒有影響，根據應力衰減觀點，在支腿數量變化的時候，只影響支腿部位局部的應力狀況， 對于遠離支腿部位的地方沒有影響。

3 ?結 論

通過對裂紋在多種情況下應力場的分析，可以得出以下結論：

（1）裂紋長軸長度和角度的變化對應力場影響顯著，其余因素對應力場影響不明顯。

（2）隨著裂紋長軸長度的變大，等效應力值也顯著變大，等效應力最大點隨著裂紋長軸長度的變大，由長軸邊緣位置移到裂紋短軸邊緣位置。

（3）隨著裂紋長軸角度的變大，等效應力最大點隨著裂紋長軸角度的變大，由長軸邊緣位置移到裂紋短軸邊緣位置，裂紋長軸角度小于22.5°時，等效應力緩慢增長;裂紋長軸角度大于22.5°時，等效應力值下降;在22.5°～45°之間，等效應力值緩慢下降;超過45°時，等效應值迅速下降。

參考文獻：

[1]Kim Y， Kim J， Ahn J， et al. Effects of local wall thinning on plastic limit loads of elbows using geometrically linear FE limit analyses[J]. Engineering Fracture Mechanics， 2008， 75： 2225-2245.

[2]Raju， IS. Calculation of Strain Energy Release Rate with higher order and singular finite element[J]. Engineering Fracture Mechanics， 1987， 28：251-274.

[3]解德. 斷裂力學中的數值計算方法及工程應用[M]. 北京：科學出版社，2009 ：9-20.

[4]鄭耀輝，崔林琳.壓力容器邊緣應力的有限元分析[J].沈陽航空工業學院學報，2001，18（3）：12-16.

[5]祁建磊，路智敏.含裂紋壓力容器的安全評定及強度因子求解[J].化工設備與管道，2016，53（3）：15-27+84.