橢圓封頭—筒體結構可靠性設計公式推導

羅惠敏 楊溪榮 韋權權

摘 ?????要： 依據國際安全聯合委員會（JCSS）推薦使用的由拉克維茨等出的JC法（可靠度計算方法）和第四強度理論，推導了壓力容器橢圓封頭和薄壁圓形筒體的可靠度計算公式。采用ANSYS中蒙特卡洛可靠度計算方法對上述公式的正確性進行了驗證，同時分析了對結構可靠度影響較大的因素。以上研究為壓力容器的可靠性分析提供了一定的參考。

關 ?鍵 ?詞：JC法;可靠度分析;蒙特卡洛;壓力容器

中圖分類號：TQ 052 ??????文獻標識碼： A ??????文章編號： 1671-0460（2019）08-1894-04

Abstract： Based on the JC method （reliability calculation method） and the fourth strength theory proposed by the International Security Council （JCSS）， the reliability calculation formula of the elliptical seal head and thin circular cylinder of the pressure vessel was derived. The correctness of the above formula was verified by Monte Carlo reliability calculation method in ANSYS， and the factors that have great influence on structural reliability were analyzed. The above research provides reference for the reliability analysis of pressure vessel.Key words： JC method;Reliability analysis; Monte Carlo;Pressure vessel

隨著石油化工行業的大型化發展，對壓力容器設計提出了越來越高的要求，不僅需要其能完成預定的功能并確保安全性，同時對其經濟性和可靠性也提出了要求。在保證壓力容器安全性的前提下，兼顧其經濟性已經具有越來越重要的意義[1]。在壓力容器設計過程中，其設計壓力、材料強度和結構尺寸等均具有隨機性，而現有標準將這些參數按照確定量處理，通過采用較大的安全系數來確保結構的安全性，顯然不能達到較好的經濟性[2， 3]。本文采用JC法[4]（可靠度計算方法）和第四強度理論，推導出壓力容器橢圓封頭和圓形筒體的可靠度計算公式，并將其應用到橢圓封頭—筒體結構的設計中，再采用ANSYS中蒙特卡洛[5]可靠度計算方法進行驗證，分析了對結構可靠度影響最大的因素，為壓力容器的可靠性設計提供參考。

1.2 ?橢圓封頭可靠度計算

橢圓封頭的應力組成同球形封頭相似，除由筒體承壓所造成的一次應力外，在連接位置還存在不連貫分布的應力。參考在實際中獲得的經驗和材料力學等力學理論能夠得知，橢圓封頭的承載狀態和一個無因變量—a/b相關，所以在a/b處于1.0～2.6范圍內時，在實際情況中使用如下的公式求出橢圓封頭的應力增大系數K [6]式（7）可以看做2K=封頭承載應力除以周向一次應力，即在a/b處于1.0～2.6范圍內時，橢圓封頭的承載的全部應力同內徑相當的球形封頭一次應力的比值為K。所以能夠推到出的功能函數如下所示：

通過JC法計算出等效的均數和方差，再進一步進行計算即可得出橢圓封頭的可靠性指標：

1.3 ?橢圓封頭—筒體結構可靠度

結構的可靠度為：

2.2 ?可靠性分析

以上一小節通過理論公式計算得到的筒體——橢圓封頭結構為研究對象，使用ANSYS建立如圖1所示的有限元模型，對上述結構進行可靠性求解。

進行求解參數設置時，將筒體內徑（R）、封頭長軸（Rt）、筒體壁厚（t1）、封頭壁厚（t2）、設計壓力（P）和屈服強度（yies）看做符合高斯分布的參數。同時定義功能函數為：

（2）求解結果Z（功能函數）靈敏度計算結果如圖3所示，對求解結果進行分析能夠得知，yies、P和t1對功能函數的影響較大，其余參數影響較小。當yies增大時，結構的承載能力提升，可靠度增大。

（4）在置信度為95%的情況下，Z<0的概率為0%，即容器的失效概率為0%，此時結構的可靠度為100%。

2.3 ?強度分析驗證

根據表1確定的設計參數在ANSYS有限元軟件中建立如圖5所示的有限元模型。

圖5中橢圓封頭和筒體的厚度均按照表1中的均值建立有限元模型，選用PLANE 182單元，并將單元特性修改為軸對稱。在筒體下面施加符合總體坐標系的Y向0位移約束，在橢圓封頭左端面施加符合總體坐標系的X向0位移約束。在筒體和橢圓封頭內表面施加5 MPa的壓力。隨后進入ANSYS的計算模塊點擊計算求得橢圓封頭—筒體模型在此條件下的應力分布如圖6所示。

從圖6中可以看出最大應力位于橢圓封頭和筒體連接處，同時筒體部分和封頭遠離連接處部分的應力較為均勻，同時在最大應力處的應力分布呈現斜紋狀和分層分布，所以對于橢圓封頭和筒體遠離連接處部分的應力應該為一次應力，對于連接處的應力是一次加二次應力。

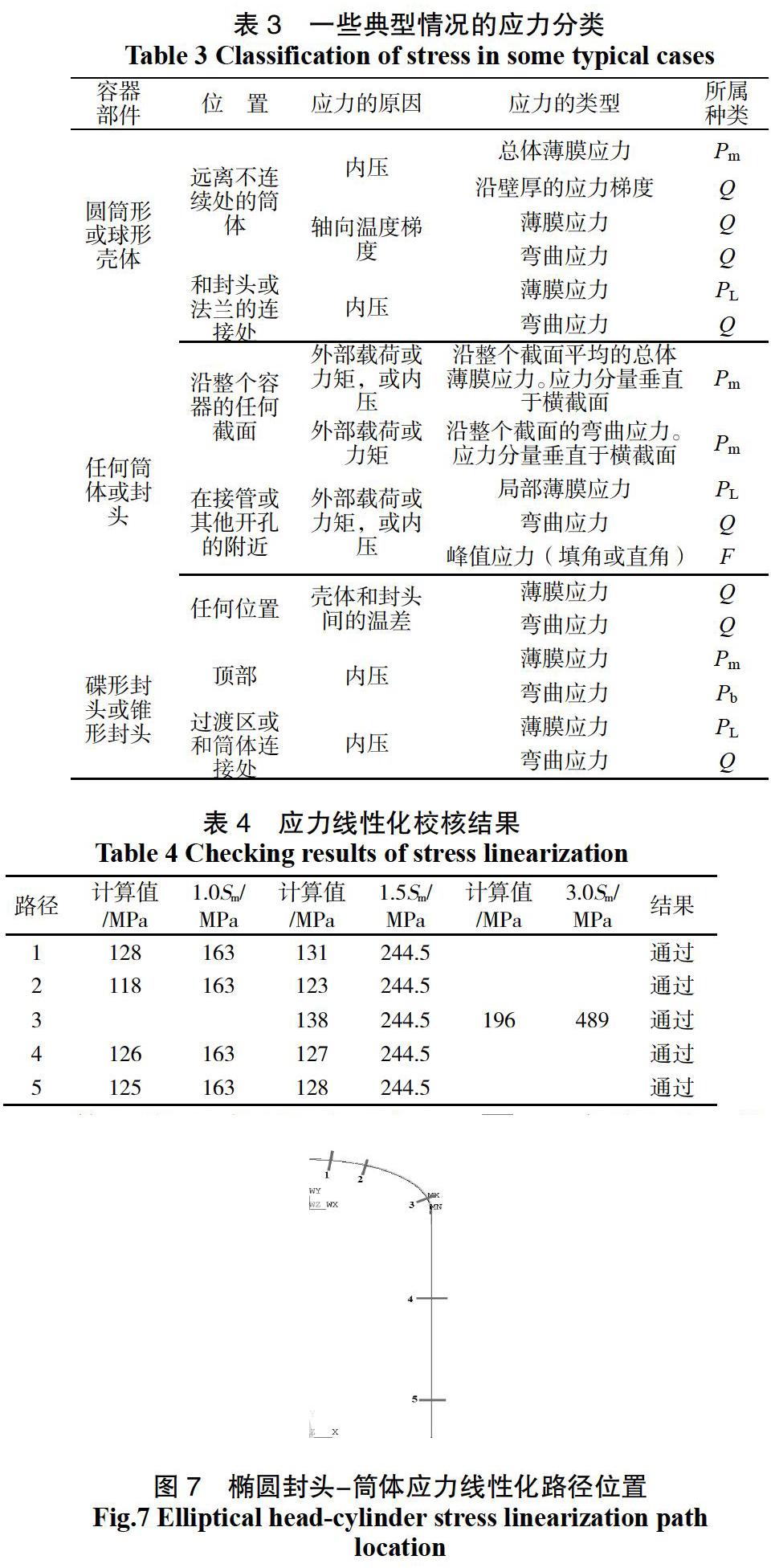
根據中國分析設計標準JB4732-1995《鋼制壓力容器——分析設計標準》（2005年確認）中規定的應力分類方法如表3所示。

同時結合上面的應力分析，應在橢圓封頭上選取兩條路徑，一條靠近橢圓封頭的左側端面，但是為了排除約束條件對應力分布的影響，該路徑距離左側端面的距離應該大于，具體位置如圖7中的路徑1所示。

同時為了保證路徑1的位置正確，應該在距離1較近的位置再做一條路徑2。在筒體和封頭模型連接處，是應力的最大位置，從保證模型安全性的角度出發，應該在此處取一條應力線性化路徑，具體位置如圖7中路徑3所示。為了保證筒體的強度合格，應該在筒體上選擇兩條路徑，一條路徑靠近筒體下端面，但是距離要大于，一條路徑位于筒體的中部，所做路徑的具體位置如圖7中路徑5和路徑4所示。最終所有路徑的位置如圖7所示。

根據JB4732-1995《鋼制壓力容器—分析設計標準》（2005年確認）中規定的16MnR在100 ℃下的設計應力強度為163 MPa，根據圖5中所示的計算結果可知，本文選用的筒體—橢圓封頭模型的最大應力為196.839 MPa，大于16MnR的設計應力強度163 MPa，但是小于1.5倍的設計應力強度244.5 MPa。

如果確定結構中不包含一次應力，那么可以根據標準中的校核方法認定該結構的強度滿足標準要求，但是根據上述分析，可知該結構中包含了一次應力，所以應該按照圖7中所示的路徑位置，在ANSYS有限元軟件中使用應力線性化模塊做相對應的路徑。并依次提取出所做路徑的薄膜應力和薄膜加彎曲應力進行校核。對圖7中的5條應力線性化路徑校核結果如表4所示。

根據表4中的應力線性化校核結果，知道使用可靠性分析設計方法確定的橢圓封頭和筒體厚度是滿足分析設計標準對結構的強度要求。

3 ?結 論

壓力容器設計過程中，設計壓力、筒體內直徑和材料屈服強度等因素不是相互獨立的，相互間存在一定的相關性，所以有必要對壓力容器進行可靠性分析和設計。本文使用JC法推導出壓力容器筒體和橢圓封頭可靠度計算公式，同時通過計算軟件中的可靠度求解方法對結構進行建模求解。最后使用ANSYS有限元軟件中的強度分析模塊對橢圓封頭—筒體模型進行分析計算，并按照中國現行的分析設計標準，對結構上的路徑進行應力分類，并分別校核其計算結果，可以得知該結構的強度滿足標準要求。所以該可靠度計算公式可用于筒體和橢圓封頭的可靠性設計。

參考文獻：

[1] 路智敏.壓力容器殼體的可靠性設計及在固體火箭發動機殼體上的應用[D].北京：北京交通大學，2009.

[2]Yao C. LRFD calibration of bridge foundations subjected to scour and risk analysis[J]. Dissertations & Theses - Gradworks， 2013.

[3]Marquez Balderrama J. A simplified method to develop LRFD preliminary design charts for prestressed concrete bridges[J]. Dissertations & Theses - Gradworks， 2015.

[4]Rackwitz R， a B. Flessler. Structural reliability under combined random load sequences[J]. Computers & Structures， 1978， 9（5）： 489–494.

[5]孫博.燒結爐壓力容器的應力分析與可靠性分析[D]. 沈陽：沈陽工業大學，2014.

[6]Cai B， et al. Exploratory study on load and resistance factor design of pressure vessel for subsea blowout preventers[J]. Engineering Failure Analysis， 2013， 27（1）： 119–129.

[7]胡瀚元，謝禹鈞，黃新，等.基于有限元法的高壓球罐強度可靠性分析[J].當代化工，2005，44（01）：187-189.