基于加權聯合靈敏度方法的損傷識別研究
汪振東 紹興文理學院土木工程系
1 引言
近年來,在民用、機械和航空等眾多工程界中,利用實測動態數據進行結構損傷檢測已成為一個較為熱門的研究方向[1~4]。在目前已經提出的眾多根據實測動態數據進行的靈敏度分析方法中,將頻率靈敏度與振型靈敏度進行共同分析的聯合靈敏度方法有著良好的發展前景[5]。頻率與振型聯合靈敏度在無誤差的情況下對結構損傷的檢測定位較為精確,但是在有誤差影響的情況下計算結果還是存在較大的誤差,而實際工程中誤差是必然存在不可避免的,因此,對于聯合靈敏度在有誤差影響下的改進有著極其重要的意義。在通過靈敏度方法對結構進行損傷識別時,往往會碰到奇異矩陣的計算,而奇異矩陣的計算結果常常導致誤差很大,為解決該問題,學者們提出了嶺估計方法來進行結果修正,可以在很大程度上提高參數估計的可靠性和穩定性。本文在振型和頻率聯合靈敏度方法的基礎上對其進行加權處理,進而得到一種新的加權聯合靈敏度方法,再通過嶺估計的方法對新方法的計算結果進行修正,并通過一個有31個單元的結構模型對新的加權聯合靈敏度方法進行驗證。
2 頻率與振型的聯合靈敏度方法
本文所涉及的靈敏度方法主要是通過得到結構的頻率矩陣和振型矩陣的改變量,從而聯合計算得到靈敏度。而固有頻率的平方即是特征值,在求解特征值靈敏度問題時,有兩個重要的約束方程,公式(1)和(2):
式中:
K——結構的剛度矩陣;
M— —結構的質量矩陣;
λj— —結構的第j階特征值;
Φj— —結構的第j階特征值所對應的特征向量。當結構第i個單元發生結構損傷時,由公式(1)和式(2)對第i個單元的損傷參數求導即可得到:

式中:
αi— —第i個單元的損傷系數;
n— —所取的結構的自由度;
Ki——第i個單元的單元剛度矩陣。
結構某個單元在損傷前后的特征值的變化量Δλ就等于該單元損傷后的特征值去減損傷前的特征值,結構損傷前后的特征向量的變化量ΔΦ也是一樣,即:

而結構的一階特征值和特征向量利用泰勒級數展開,結構損傷前后的特征值和特征向量變化量又可以近似表示成:
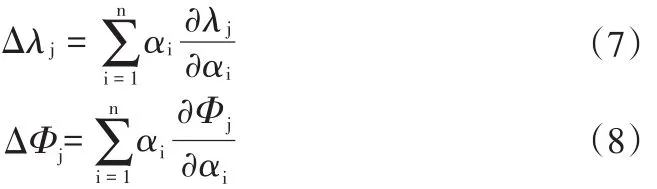
式中:
N— —結構所有的總單元數。在這基礎上根據結構所測的前m階模態和r階自由度,結構的特征值和特征向量的一階靈敏度S1和S2可以表示成:

將公式(9)和式(10)聯立,特征值特征向量兩個靈敏度通過拉直運算可以合并到一個矩陣中從而組成一個新的聯合靈敏度:
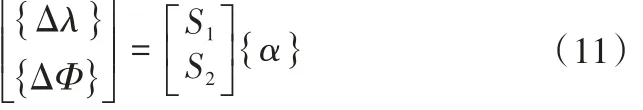
該靈敏度就是特征值與特征向量的聯合靈敏度,也就是頻率與振型的聯合靈敏度。
3 加權聯合靈敏度方法
頻率與振型的聯合靈敏度計算方法同時繼承了頻率靈敏度和振型靈敏度的優點,在不需要測得所有頻率和陣型的時候就可以較為準確的判斷是否損傷,通過廣義逆運算甚至可以計算結構的損傷程度。
但是在實際運用中,頻率與振型的聯合靈敏度矩陣中的特征值和特征向量部分在數量級上往往有104左右的差距,數量級上的巨大差距在一定程度上造成了計算時的誤差。因此,在計算時在特征值部分乘上一個權系數q[如公式(12),通過縮小特征值和特征向量之間數量級上的差距從而縮小計算誤差。而這個權系數應在一定的范圍內時起到較小誤差的作用,當超出這個范圍時,反而會增加誤差。

通過對加權頻率和振型聯合靈敏度廣義逆矩陣的計算可以得到結構各單元的損傷程度。
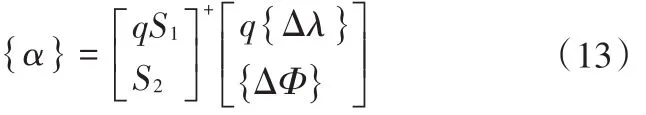
嶺估計方法可以很大程度上提高參數估計的可靠性和穩定性。本文將加權帶入嶺估計方法中,再對計算結果進行修正。
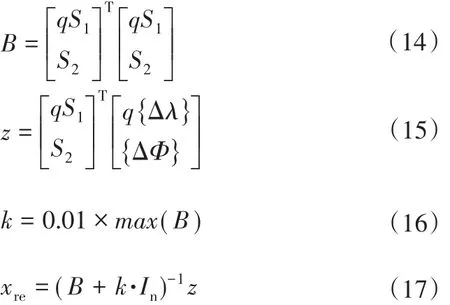
4 算例分析
建立如圖1所示的一個有31個單元的結構模型,其中彈性模量E=200GPa,材料密度ρ=7.8×103kg/m3,橫向和豎向的直桿的長度L=1m,桿件的截面積A=0.004m2,結構的左下角和右下角均為固支,振型的誤差取3%,頻率的誤差取0.3%,計算時只選取結構的前2階模態和前10個自由度。通過減少單元的剛度矩陣來模擬損傷,再通過加權聯合靈敏度方法計算,然后通過嶺估計進行修正。

圖1 31個單元結構模型圖
將第15號單元的單元剛度矩陣減小30%來模擬第15號單元損傷。由于加權聯合靈敏度矩陣的條件數在權系數取1×10-4左右時最小,因此本算例中權系數取1×10-4,通過嶺估計修正后的結果如圖2。加權聯合靈敏度矩陣的條件數為289.7656,而未加權聯合靈敏度矩陣條件數往往在105以上,由此可以看出加權方法可以很大程度上減小加權聯合靈敏度矩陣的條件數。由圖2中可以看出在模態參數較少和有噪聲干擾的情況下,加權聯合靈敏度方法可以準確地判斷出損傷位置,且對于第15號單元損傷程度的計算在0.26左右浮動,與真實值0.3較為接近。
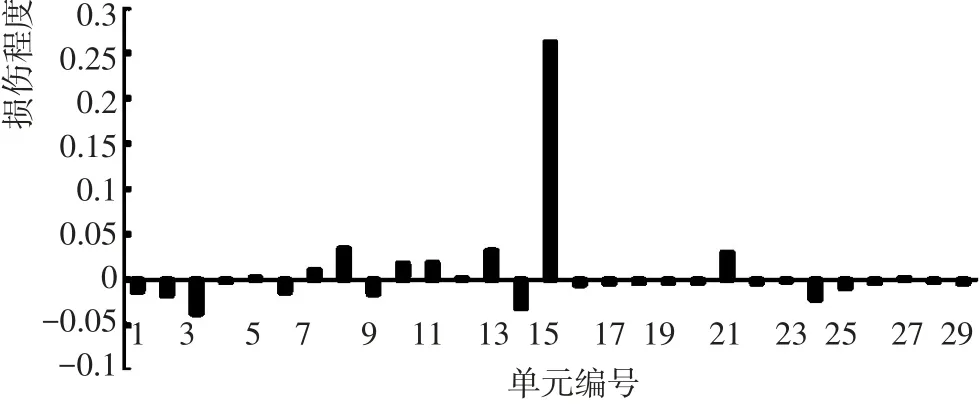
圖2 q=1×10-4時計算結果圖
5 結論
頻率與振型聯合靈敏度在無誤差的情況下計算結果較為準確,但是在有誤差影響的情況下計算結果誤差較大,而其誤差大的原因之一是計算過程中的靈敏度矩陣特征值部分和特征向量部分數量級上有104左右的差距,數量級上的巨大差距導致矩陣的條件數極大,從而影響計算結果。本文提出的加權頻率與振型靈敏度的方法從這個角度入手,通過給靈敏度矩陣的特征值部分加權來減小特征值和特征向量部分的差距,從而減小誤差。
通過一個有31個單元的模型算例,模擬單個單元損傷并進行計算,結果表明條件數在權系數取到1×10-4時最小且在該取值下可以準確的識別損傷位置,未損傷單元的誤差和損傷單元的的損傷程度計算誤差上都較小,但在損傷程度的計算方面還存在一定的誤差,如何進一步縮小誤差還有待研究。

