一元一次方程解法“糾錯”
2019-12-17 09:06:40許玉紅
初中生世界 2019年41期
文 許玉紅
對于一元一次方程,絕大多數同學都能掌握解方程的步驟,但在解方程過程中出現的“錯誤”卻各種各樣。我們要學會“糾錯”,才能少出錯。
例1 解方程7-2x=3+4x。
【錯解】移項得2x+4x=3-7,
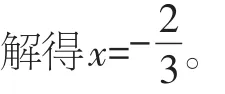
【分析】移項法則的依據是等式性質,上述移項省略了等式變形的過程。同學們如果只背熟移項要變號而未能理解移項的本質,那么就會出現像錯解中-2x沒有移項也變號,而4x移項卻不變號的錯誤。
【正解】移項得-2x-4x=3-7,

例2 解方程-3(x+1)=9。
【錯解】去括號得-3x+1=9,

【分析】同學們運用去括號法則時,主要用乘法分配律。初中階段學習了負數,所有的運算都要考慮結果的符號。因此括號前出現負數時,同學們容易發生錯誤:一是去括號時忘記變號,二是去括號時漏乘系數。
【正解】去括號得-3x-3=9,
解得x=-4。

【錯解】去分母得2(2x-1)=2x+1-1,
解得x=1。
【分析】去分母的依據是等式基本性質二:等式兩邊同時乘或除以同一個不為零的數,所得結果仍然是等式。錯解中方程兩邊同乘分母的最簡公分母時,漏乘整數項導致錯誤。
【正解】去分母得2(2x-1)=2x+1-6,

【錯解】化簡得5(x-2)-2(x+1)=30,
解得x=14。
【分析】分母中的小數化為整數時,利用的是分數的基本性質:分子、分母同乘或除以一個不為零的數,分數的大小不變。有的同學對概念模糊,混淆了分數的基本性質和等式的基本性質。
【正解】化簡得5(x-2)-2(x+1)=3,
解得x=5。
例5 解方程6x=16。

【分析】系數化為1,應除以未知數x的系數,不能除反了,而且最后結果也要化成最簡分數。

猜你喜歡
數學雜志(2021年6期)2021-11-24 11:12:00
中學生數理化(高中版.高二數學)(2021年5期)2021-07-21 02:14:46
數學年刊A輯(中文版)(2021年1期)2021-06-09 09:31:56
民用飛機設計與研究(2020年4期)2021-01-21 09:15:02
中等數學(2020年6期)2020-09-21 09:32:38
中等數學(2019年6期)2019-08-30 03:41:46
電子制作(2018年18期)2018-11-14 01:48:24
中學生數理化·七年級數學人教版(2018年4期)2018-06-28 03:26:30
山東工業技術(2016年15期)2016-12-01 05:31:22
中國中醫藥現代遠程教育(2014年11期)2014-08-08 13:23:44

