回眸“方程”的發展歷程

文 吳秀蘭

代數中引進未知數，具有劃時代的意義，猶如遠古時代的火、航海時代的指南針、工業革命時期的蒸汽機。方程作為人類思想的一次飛躍，是繼算術思想之后的又一重要的數學思想，折射出人類的智慧。今天吳老師帶著同學們一起坐上時光機，穿越到古代，看看方程的發展歷程。

方程是代數史中重要的研究課題之一，它最早出現于我國的《九章算術》中。這里的“方程”其實是指一次方程組。例如：求解三元一次方程組：

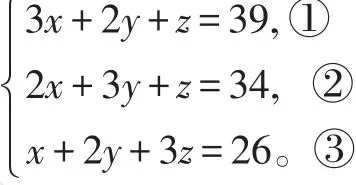
《九章算術》沒有提出表示未知數的符號，而是用算籌將未知數的系數和常數項排列成一個（長）方陣（如下圖），故稱為“方程”。

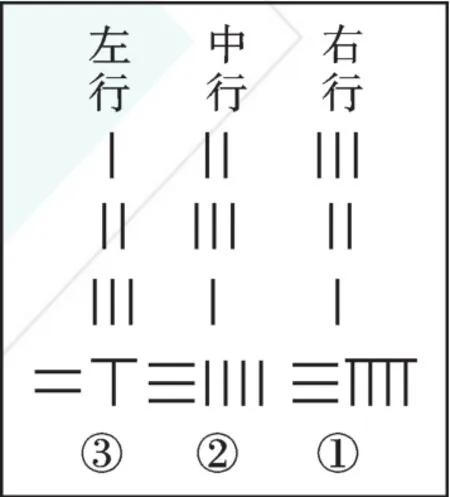
在世界數學史上，對方程的原始記載有著不同的形式。約3600多年前，古埃及人寫在紙草書上的數學問題就涉及了含有未知數的等式。公元825年左右，數學家花拉子米為研究方程，寫過一本《對消與還原》，書里詳細介紹了方程的解法——還原與對消，即移項與合并同類項。宋元時期，中國數學家創立了“天元術”，用“天元”表示未知數進而建立方程，這種方法的代表作是數學家李冶寫的《測圓海鏡》。書中的“立天元一”相當于“設未知數”，所以在簡稱方程時，將未知數稱為“元”，如含一個未知數的方程叫“一元方程”，一元一次方程中的元就來自天元術。

到了17世紀，歐洲數學家韋達完成了數學的符號化。法國數學家笛卡爾最早提出用字母來表示未知數，把字母和普通數字同樣看待，用運算符號和等號把字母與數字連接起來，就形成了含有未知數的等式。后來經過不斷簡化和改進，方程逐漸演變成現在的表達形式，例如6x+8=20，5x+2=10，x-5=2等，才有我們今天“方程”的符號化系統。

隨著數學研究范圍的不斷擴充，方程被普遍使用，它的作用越來越大。列算式解應用題用的是小學的逆向思維；列方程解應用題運用的是正向思維，可以直接快速解決問題。由算術方法到方程方法，是數學思想的一次飛躍。接下來，我們再一起看古人如何利用一元一次方程的知識來解決實際問題。

例如，大數學家丟番圖的墓碑上刻了這樣一個經典問題：

過路人啊，這里安葬著丟番圖，下面的數字可以告訴你他生命有多長。他生命的六分之一是愉快的童年；再過了生命的十二分之一，他的面頰上長了細細的胡須；又過了生命的七分之一，他走進婚姻的殿堂；五年后天賜貴子，他感到很幸福。可是，命運給他兒子的光輝燦爛的生命只有他生命的一半長。自從兒子死后，他的悲傷只有用研究數論去解脫。又過四年，他也結束了塵世的生涯。

我們一起來算一算丟番圖的年齡。

丟番圖是第一位懂得用符號代表數來研究問題的人。同學們，我們用方程來解決這個問題，是不是相當便捷？

看了這么多，相信大家一定能體會到方程不僅形式簡單，而且有非常豐富的內涵。在生活中，只要我們稍加體會，方程思想的價值便隨處可見。古人在數學問題上都能不怕困難，勇登高峰，我們更應該向他們學習。讓我們坐上時光機，返回現代吧。方程是從現實生活到數學的一個提煉過程，一個用數學符號提煉現實生活中的特定關系的過程。在開始學習方程時，同學們用符號表示數值關系，面臨的一個困難是如何把問題的情境翻譯成方程。大家要學會把日常生活中的自然語言等價地轉化為數學語言，得到方程，進而解決有關問題。本次旅行結束，希望大家有所收獲！