復合材料結構與表面壓電材料動態布局優化
單 堯,余 兵,牛 斌
(1.大連理工大學 機械工程學院,遼寧 大連 116024;2.上海宇航系統工程研究所,上海 201109)
0 引言
工程結構大多處在動態載荷環境中,結構受動態載荷產生的振動會影響結構的性能與使用壽命,所以抑制結構的振動具有重要意義。壓電材料是一種可實現機械能與電能相互轉化的智能材料。壓電材料的逆壓電效應可以將電能轉換為機械能,利用該特性,壓電材料被廣泛用于主動或被動控制結構振動[1]。通過優化結構本身材料的分布實現最小化結構振動響應的研究已得到廣泛研究[2]。近年來,學者們通過引入壓電材料來改善結構的動態性能,如Kang和Zhang通過優化結構表面壓電材料的分布研究了結構振動的主動控制[3]。由于脆性壓電陶瓷材料的可加工性差,所以難以實現加工任意拓撲的壓電片,因此,一些學者提出了通過優化指定規格壓電片的布局代替尋找最優的壓電材料拓撲,如Quek等[4]利用直接搜索法得到了抑制結構指定模態自由振動的壓電片的最優分布;Gao等[5]利用遺傳算法研究了抑制振動板噪聲傳遞的壓電傳感器與致動器的位置優化問題。文獻[2-5]的研究工作主要通過單獨優化支撐結構的拓撲或結構表面的壓電材料分布實現結構的振動抑制。本文將優化復合材料支撐結構的鋪層與材料選擇,同時優化結構表面給定尺寸的矩形壓電片布局,實現最小化結構振動響應。數值算例表明,使用該優化方法可提高結構振動抑制的效果及優化設計的制造性。
1 壓電結構振動分析
壓電材料的壓電效應可分為正壓電效應(機械能轉化成電能)與逆壓電效應(電能轉化成機械能)[6],分別表示為
D=eε+κE
(1)
σ=Cε-eE
(2)
式中:ε,σ分別為應變向量與應力向量;C為彈性矩陣;e,κ分別為壓電應力常數矩陣和介電常數矩陣;E,D分別為電場強度向量與電位移向量。

圖1 復合材料層合板示意圖與橫截面圖
本文采用壓電材料作為致動器,與外加電壓相比,由壓電材料正壓電效應產生的電荷量非常小,對壓電材料的作用可忽略不計。因此,我們只考慮壓電材料的逆壓電效應。針對圖1所示復合材料層合結構,只考慮壓電材料的逆壓電效應[7],利用有限元法得到的壓電感應力向量fin為
fin=-Kuφφ
(3)
式中Kuφ,φ分別為壓電矩陣和電勢。
不考慮阻尼,引入壓電材料后振動結構的控制方程為
(4)

2 振動作用下壓電結構優化列式
2.1 離散材料優化(DMO)法材料模型
與各向同性材料不同,復合材料具有方向性。所以,復合材料結構的性能與每一層的纖維分布與鋪設角度有關。在這里對于復合材料結構的建模我們參考DMO法[8],這種方法通過選擇預先設定的備選材料來實現復合材料結構的鋪層材料、鋪設角度及鋪層順序的優化;其中備選材料可以是不同種類的材料,也可以是鋪設角度不同的同一種纖維增強復合材料。本文通過將備選材料設置為泡沫材料和不同鋪設角度的纖維復合材料,實現各層不同纖維角度的分析與優化,以及纖維材料和泡沫材料的拓撲設計。應用DMO法后每層的本構關系矩陣Ql與質量密度ml分別為

(5)
(6)
式中:ξi,Qi和mi分別為第i種備選材料的權函數,本構關系矩陣和質量密度;nl為第l層備選材料總數。
本文中使用的壓電材料為各向同性材料,基于DMO法我們將壓電層備選材料設置為壓電材料與人為定義的孔隙材料,并引入區域(Patch)設計變量[8],從而得到給定尺寸的矩形壓電片的分布。第l層的壓電應力矩陣el為
el=ξ1e1+ξ2e2
(7)
式中:ξ1,ξ2分別為壓電材料和人為定義孔隙材料的DMO權函數;e1,e2分別為壓電材料和人為定義孔隙材料的壓電應力矩陣。
2.2 目標函數與壓電結構優化列式
衡量結構振動的優化指標很多[9],選取結構局部位移作為描述結構振動響應的指標為
g=UTLU
(8)
式中:U為結構位移幅值向量;L為索引矩陣,表示需要優化響應節點的位置;上標T為轉置運算。
引入式(8)與式(4),可得優化列式如下:

0 (9) 利用伴隨法求得目標函數對設計變量的靈敏度為 (10) (11) 本節以圖1所示結構作為算例來說明該方法的有效性。該結構(見圖1)為左側固定的層合懸臂板結構,共5層(每層厚為0.2 mm)。該懸臂板長為1 m,寬為0.5 m。將結構劃分為40×20的有限元網格。第一層全為碳纖維復合材料,備選鋪設角度為[0°,±45°,90°],第二層到第五層除了碳纖維材料,還有各向同性泡沫材料,第六層為各向同性的壓電材料與人為定義的材料屬性很小的孔隙材料。初始設計結構為各備選材料均勻分布。在懸臂板右端中心位置(A點)施加一個垂直板面的f=Feiωpt,F為外加機械載荷的幅值向量,其中幅值為10 N。根據初始結構的自由振動頻率,選取激勵頻率為35 Hz(在第二、三階的自由振動頻率之間)。第六層的壓電片厚為0.2 mm,長和寬均為50 mm。外加電壓的頻率和機械載荷的頻率相同且幅值為1 V。選取全部節點的響應作為優化目標,即L為單位矩陣。壓電材料的性能參數如表 1所示,η=40%。使用移動漸近線法(MMA)[10]求解式中的優化問題。壓電材料、碳纖維復合材料和各向同性泡沫材料的彈性模量E、質量密度ρ、剪切模量G、泊松比υ及壓電應力系數e分別如表1~3所示。 表1 壓電材料性能參數表 表2 碳纖維復合材料性能參數表 表3 泡沫材料性能參數表 此模型在外激勵頻率35 Hz時得到的優化設計如圖 2所示,其中第一層到第五層里的黑色短線代表碳纖維的鋪設角度;第二層和第五層空白處為泡沫材料。第六層中黑色部分代表壓電材料。灰色部分表示未粘附壓電材料。 圖2 35 Hz激勵頻率下優化設計結果 圖3為優化前、后的結構在外激勵頻率35 Hz下的位移幅值分布對比圖,為了使對比結果明顯,圖中顯示的位移幅值為放大5倍后的結果。對比圖3(a)、(b)可知,優化后的結構位移幅值明顯小于初始結構。目標函數(g)由初始的20.84下降到0.046。對比圖3(a)、(c)發現,壓電材料的機械性能可以在一定程度上減小結構的振動響應。觀察圖2可看出,纖維材料和第六層壓電材料片的分布具有較好的對稱性;泡沫材料主要分布在中間層,即第二層到第四層;對比圖3中的位移幅值分布圖,圖2中第五層的纖維材料與第六層壓電層的材料主要分布在位移幅值較大的區域。該結果充分說明了該抑振方法的有效性。 圖3 位移幅值分布圖 在本文中,壓電材料作為壓電致動器使用,其正壓電效應對結構振動產生的影響忽略不計。數值算例表明經過優化,結構的振動響應明顯減小。同時優化壓電材料的分布與結構本身可有效地實現結構振動最小化,其中壓電材料的分布說明,由壓電材料的逆壓電效應產生的力不僅可以有效地抑制結構振動,且壓電材料本身具有的剛度與質量也可以增強結構本身的機械性能。

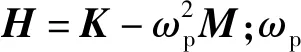

3 數值算例





4 結束語

