基本不等式的應用問題例談
葉 珊
(福建省福安市第一中學 355000)
一、求解最值問題
作為函數最值求解的一大重要工具,基本不等式在利用時要注意相應的條件“一正、二定、三相等”.特別在配湊應用時,要注意條件成立的條件,否則容易出現錯誤.
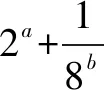
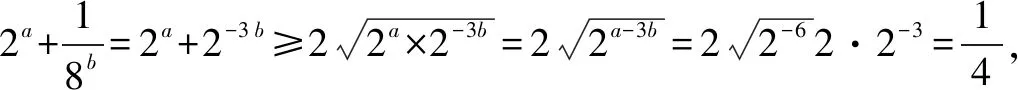
點評利用基本不等式求解代數式的最值問題中,運用時往往需對代數式進行適當地變形(常用的變形技巧是:配方、拆添項、配湊因子和平方等),創造應用基本不等式的條件,要注意應用條件“一正、二定、三相等”.
二、求解參數值問題
在解決一些參數值的求解問題時,經常借助基本不等式來處理,破解的關鍵是先通過猜測確定參數值,結合基本不等式的應用,利用基本不等式的等號成立時的條件來求解相應的參數值問題.


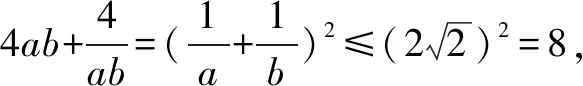
點評應用基本不等式解決一些問題時,往往要考慮等號成立時所滿足的條件,此時也為求解相應的參數值提供條件.特別碰到一些已知相關的方程問題來破解對應參數值問題時,要注意結合關系式的展開,利用基本不等式的應用,再結合相關的不等式、方程等來確定相應的參數值問題.
三、處理恒等式問題
在處理相關的恒等式問題時,關鍵是進行合理分離參數,把相關原參數的取值范圍問題化歸為相應函數的最值問題,再利用基本不等式來處理與解決.特別注意:a>f(x)恒成立?a>[f(x)]max,a 例3若函數f(x)=32x-(k+1)3x+2,當x∈R時,f(x)>0恒成立,則k的取值范圍是( ). 點評將不等式恒成立問題進行合理轉化與化歸,得以轉化為參數恒成立問題,再利用關系式的變形與配湊,借助函數的基本性質與基本不等式來解決相關的函數問題,從而得以確定參數的取值范圍.注意在此過程中,經常采用參數分離法來轉化. 利用基本不等式確定相應代數式的取值范圍問題,關鍵是巧妙借助基本不等式的變式加以應用,從不同的角度確定相應代數式的最大值與最小值即可. 例4(2018屆江蘇省揚州中學高三第四次模擬·14)已知x,y均為非負實數,且x+y≤1,則4x2+4y2+(1-x-y)2的取值范圍為____. 點評根據基本不等式的有效轉化,通過不等式的確定2(x+y)2≤4(x2+y2)≤4(x+y)2,結合參數的引入,分別利用代數式的變換以及二次函數的配方,并結合二次函數的圖象與性質來確定相應的最大值與最小值,利用兩邊夾定理加以綜合,從而得以簡單快捷破解. 作為基本不等式的一大應用,也經常用來證明一些相關的不等式問題.與綜合法相結合,借助所證明不等式的結構特征,利用基本不等式來轉化與處理. 點評利用基本不等式來證明對應的不等式時,要注意基本不等式的結構特征,與所要證明的不等式加以合理比較,進行合理的化歸與轉化.證明時的關鍵就是對相應的不等式進行必要的變形與轉化,再結合基本不等式加以應用. 在解決實際問題中,基本不等式也是用來解決最優化問題的一大工具.實際應用時,要注意基本不等式的條件與實際問題之間的聯系與區別. 例6(2017·江蘇·10)某公司一年購買某種貨物600噸,每次購買x噸,運費為6萬元/次,一年的總存儲費用為4x萬元.要使一年的總運費與總存儲費用之和最小,則x的值是____. 點評本題考查實際應用問題,基本不等式,考查應用意識,運算求解能力.此類問題與求解最值問題差不多,只是要根據實際生活問題,往往對參數的取值有一定的限制,如取整點值、取正數值等,要與實際問題相吻合.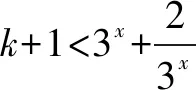
四、確定取值范圍問題

五、證明不等式問題

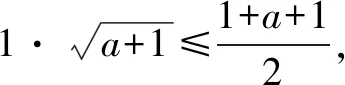
六、解決實際應用問題


