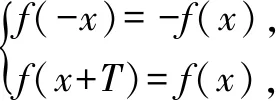高考和模擬題中的十類敗題與錯題
劉彥永
(吉林省長春市東北師范大學附屬中學 130000)
類型一:題目不嚴謹
1.(2014年高考山東理6題)直線y=4x與曲線y=x3在第一象限內圍成的封閉圖形的面積為( ).
敗因:因為第一象限內沒有坐標原點,所以直線y=4x與曲線y=x3在第一象限內不可能圍成封閉圖形,將“第一象限內”改為“第一象限及其邊界上”.
2.(2003年高考江蘇1題)如果函數y=ax2+bx+a的圖象與x軸有兩個交點,則點(a,b)在aOb平面上的區域(不包含邊界)為( ).
敗因:本題標準答案給的是C,但由a≠0知對應圖形中不包含b軸,應畫為虛線.
點評以上兩題屬于敗題,雖然不影響作答,但作為高考的權威性和引用的廣泛性,還是要注意表述上的嚴謹.
類型二:用詞不明確
3.(2017年高考北京理數8)根據有關資料,圍棋狀態空間復雜度的上限M約為3361而可觀測宇宙中普通物質的原子總數N約為1080.則下列各數中與最接近的是(參考數據:lg3≈0.48)( ).
A.1033B.1053C.1073D.1093
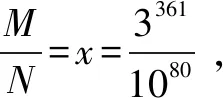

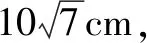
(1)將l放在容器Ⅰ中,l的一端置于點A處,另一端置于側棱CC1上,求l沒入水中部分的長度;
(2)將l放在容器Ⅱ中,l的一端置于點E處,另一端置于側棱GG1上,求l沒入水中部分的長度.

錯因:“沒入”既可以理解為入水,也可以理解為未入水,學生不同的理解就會得出不同的答案.
點評:命制試題時要注意用詞不能引起歧義.
類型三:設問不適宜
5.已知函數f(x)=2ex-x3ex.
(1)求函數f(x)在(0,f(0))處的切線方程;
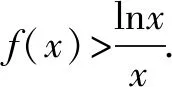

(2)若f(x)≤0,證明:a≤1-b.
敗因:對于(2)問,因為f(x)≤0,所以f(1)=a-1+b≤0,直接得結論a≤1-b.
點評上述兩題來自高三模擬試題,設問可以由條件直接快速得出,失去了壓軸題考查學生能力和區分水平的功效,在試題命制中應反復斟酌,避免這類“烏龍”題.
類型四:定義不符合
7.若f(cosx)=sin2x,則f(sinx)=( ).
A.sinxB.-sin2xC.cosxD.-cos2x
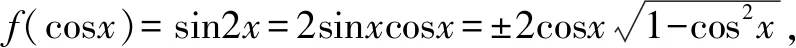
點評不符合函數定義的這類題目在教輔資料里比較多見,對函數概念不清的學生造成了很大困擾.
類型五:結果不檢驗
8.(2013年高考浙江理15題)設F為拋物線C:y2=4x的焦點,過點P(-1,0)的直線l交拋物線C于A,B兩點,點Q為線段AB的中點.若|FQ|=2,則直線l的斜率等于____.

點評在數學解題過程中,要注意變形的等價性,也要注意對結果的檢驗,尤其是出現答案多解的情況更要提高警惕.
類型六:“模型”不存在
9.一個等比數列{an}共有2n+1項,奇數項之積為100,偶數項之積為120,則an+1為.
錯因一方面,由a1a3…a2n+1=100,a2a4…a2n=120作商有

點評這類錯題可謂“深藏不露”,若不深入探究不知“錯”在哪里,還會自以為“是”,因此是流傳更為廣泛的一類錯題.
類型七:“模型”不唯一
11.(2010年福建高考理12題)若一個底面是正三角形的三棱柱的正視圖如圖1所示,則其表面積等于.
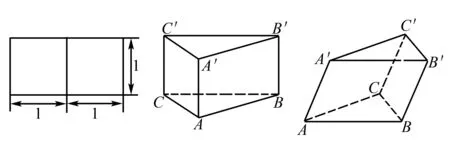
錯因標準答案是按照圖2給出,事實上,根據條件得到的三棱柱可能是圖3(調整角度后的圖,便于讀者理解),即側棱未必與底面垂直,這樣本題的答案就不確定了.
點評這類錯題產生的原因就是條件過于“開放”,導致模型不唯一,此類錯題多出現在立體幾何試題中,如,給定的三視圖對應的幾何體未必是唯一的.
類型八:條件不相容
12.已知定義在R上的奇函數f(x)滿足條件f(x+2)=-f(x),當-2 A.-1 B.0 C.2017 D.2018 事實上,定義在R上的奇函數f(x)滿足則f(x+2)=-f(x),則也有f(-x-2)=f(x),即函數的圖象關于直線x=-1對稱,與-2 點評題目的已知條件制約關系太多,若充分挖掘就會發現自相矛盾,這也是一類流傳較多的錯題,值得關注. 類型九:答案不正確 13.(2005年福建理12題)若f(x)是定義在R上的以3為周期的奇函數,且f(2)=0,在區間(0,6)內f(x)=0的解的個數的最小值是( ). A.3 B.4 C.5 D.6 錯因本題標準答案給的是C,根據條件容易知道f(1)=f(2)=f(3)=f(4)=f(5)=0,忽略了f(1.5)=f(4.5)=0,故正確答案應該是7. 類型十:試題不可解 14.不等式(x-1)2 點評可以將本題改編為“不等式(x-1)2>logax對x∈(0,1)恒成立,求實數a的取值范圍.”遇到錯題時可以適當交給學生探究和討論,培養學生發現問題和解決問題的能力. 美國著名數學教育家波利亞說過,掌握數學就意味著學會解題,而想要學會解題,好的數學題目是關鍵.我們急需深刻總結和反思命制好題的經驗,更要汲取錯題命制的教訓,力爭命制出高質量的好題.