尺規作圖
——過圓外一點作圓的切線方法歸納
胡小華
(江蘇省南京市金陵中學河西分校 210036)
尺規作圖是初中平面幾何中的重要知識,是中考的熱門題型,學生需綜合運用所學的知識,多角度思考問題.在初三第一輪復習時,我設計了這樣一個問題“過圓外一點A作⊙O的切線,尺規作圖,保留作圖痕跡,并說明作圖的依據,比一比誰的畫法多”.
學生作品展示
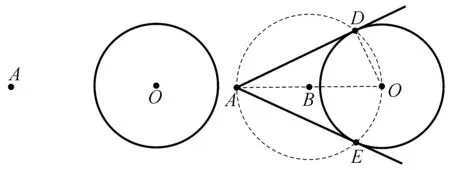
圖1
方法一:利用直徑所對的圓周角是直角.
連接AO,以AO為直徑作⊙B,⊙B與⊙O相交于D、E兩點,則AD,AE即為所求作的切線.
理由:⊙B中∵AO是直徑,
∴∠ADO=90°即OD⊥AD.
∵AD經過半徑OD的外端,
∴AD與⊙O相切.
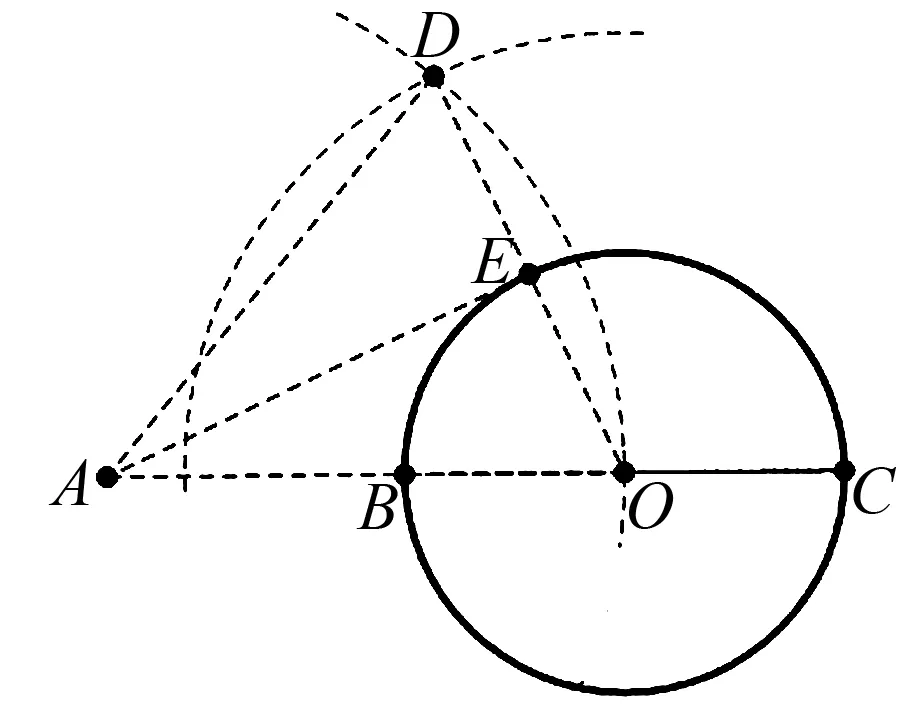
圖2
該方法是由切線想到垂直,構造直角的常用方法之一是利用直徑所對的圓周角是直角這一定理.再由切線的判定方法:過半徑外端,并且垂直于半徑的直線是圓的切線.切線的作法即轉化為主要考慮作半徑的垂線的方法,聯系初三剛學過的知識,我們首先想到的是直徑所對的圓周角是直角這一定理,這一方法也就順其自然而產生.
方法二:利用“等腰三角形三線合一”的性質作垂直.
以O為圓心,BC長為半徑作弧,以A為圓心,AO長為半徑作弧,兩弧交于點D,OD與⊙O相交于點E,連接AE,則AE即為⊙O的切線.另一條切線也可以用同樣的方法作出.
理由:∵AO=AD,
OD=BC=2OE,
∴E為OD的中點.
∴AE⊥OD,
∴AE與⊙O相切.
要作切線想到垂直,而利用等腰三角形三線合一的性質也是我們常見的構造垂直的方法之一.
方法三:利用勾股定理的逆定理構造垂直.
分析:先假設切線畫出來了,則斜邊長為AO長,一條直角邊長為半徑r,根據勾股定理可以求出另一條直角邊的長.

圖3
作∠DCH=90°,在CH上截取半徑r,交CH于點G,以G為圓心,AO長為半徑作弧,交CD于點F,則CF長即為所求作的切線長.
以A為圓心,CF長為半徑作弧交圓O于點E,連接AE,則AE即為所求作的一條切線.
理由:∵∠C=90°,
∴FC2+CG2=FG2.
又∵AO=FG,CG=OE,FC=AE,
∴AE2+OE2=AO2.
∴AE⊥OE,
∴AE是⊙O的切線.

圖4
該作圖方法是利用勾股定理的逆定理構造直角,想法比較獨特,通過先構造直角找到三邊關系,再利用三邊關系構造直角,從而創造切線.學生的思維讓人眼前一亮.
方法四:利用相似作垂直證半徑.
延長AO到D,使得OD=OA.以D為圓心,以⊙O直徑長為半徑作弧,以O為圓心,OA長為半徑作圓,交弧于點F,連接AF.過O點作OE⊥AF,交AF于點E,則AE即為所求作的切線.
證明:∵AD為直徑,
∴∠AFD=90°.∵OE⊥AF,∴OE∥DF,
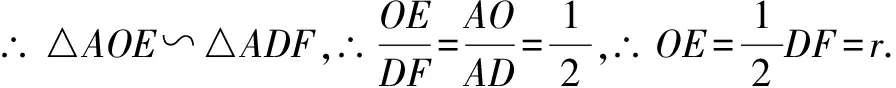
前三種方法均是連半徑,作垂直,第四種方法是作垂直證半徑,剛好復習了初中階段的證明切線的兩種方法,也是學生綜合運用知識解決問題能力的一種體現.
在復習期間這樣一個開放性的問題激發了學生學習的熱情和潛能,圍繞數學問題展開的思維碰撞,無不是學生學習主動性、能動性和創造性的綜合體現.在解決問題的過程中復習了初中階段常見的構造垂直的幾種重要方法,我不禁感嘆“只要給學生一個舞臺,他們必將還我一片精彩”!

