物流配送中多車多點路徑規劃算法研究

李淑飛 駱劍鋒

摘? 要： 物流配送中常用的Dijkstra、Floyd、A*等最短路徑算法只能計算兩點之間的最短路徑，沒有帶約束條件和回程規劃。多車多點路徑規劃算法利用神經網絡對收送貨地點進行分區，用百度地圖API計算各點之間的最短路徑，通過繞行遍歷思想計算繞行貢獻值，利用貪婪思想在車輛限載重、限路程的情況下組合回程，從而形成最優路徑方案。該算法已用在物流企業的多車多點路徑規劃云平臺上，大大提高了物流配送效率。

關鍵詞： 多車多點;最短路徑;繞行貢獻值;規劃算法;物流配送

【Abstract】： The Shortest path algorithms such as Dijkstra， Floyd， and A* commonly used in logistics distribution can only calculate the shortest path between two points， without constraints and backhaul planning. The multi-vehicle multi-point path planning algorithm uses neural network to partition the receiving and delivering places， and uses Baidu Map API to calculate the shortest path between the points，and the detour contribution is calculated by detour traversal idea， and the greedy idea is used to combine the backhaul under the condition of Limited vehicle load and distance， thus forming the optimal path scheme. This algorithm has been used in multi-vehicle multi-point path planning cloud platform of logistics enterprises， which greatly improves the efficiency of logistics distribution.

【Key words】： Multi-vehicle multi-point; Shortest path; Detour contribution value; Planning algorithm; Logistics distribution

0? 引言

在物流配送活動中，物流配送路徑的最優化問題，是物流配送系統優化中關鍵的一環。隨著配送路網的日趨復雜，配送成本日益增大[1]，在物流配送中規劃合理的配送路線，避免迂回運輸與重復運輸，有利于節省配送費用，降低物流成本，提高物流配送的效率和經濟效益。

物流配送問題是典型的組合尋優問題[2]，常用的路徑最優算法有Dijkstra[3]、Floyd、A*等算法[4]。Dijkstra算法是經典的廣度優先算法，該算法的主要特點是以起始點為中心搜索所有與其連接的點，從中心向外層延展，直到延展到終點為止，因此能夠有效解決單源最短路徑問題[5]。Floyd算法是經典的深度優先算法，該算法利用動態規劃思想，尋找給定的加權圖中多源點之間最短路徑，因此能夠有效解決任意兩點之間最短距離[6]。A*算法是基于啟發式的最短路徑算法，是一種靜態路網中求解最短路徑最有效的直接搜索方法，通過計算函數的慢相對最優解來篩選出發點周圍的后繼點[7]。這些算法都是求兩頂點之間的最短路徑，并且沒有帶約束條件，也沒有規劃回程。

現實物流配送中，可能有不同的收送貨地點、不同的收送貨重量，車輛也有限重、限程、限時等多條件的限制，如何合理安排車輛，使得車輛在限制負載、限制行程的情況下遍歷所有客戶，并且規劃回程的路徑方案最優，本文提出了多車多點路徑規劃算法。

1? 多車多點路徑規劃算法思想

1.1? 繞行遍歷思想

多車多點路徑規劃算法主要是對多車輛在限制負載、限制行程的情況下遍歷所有客戶，而且還能規劃回程的最短路徑方案，其核心是繞行遍歷思想。

假設由S點為起始點，現在要去A、B兩個地點去收送貨，兩地間的距離單位為km，如圖1所示，求要規劃回程的最短路徑。

從起始點出發，要遍歷所有點，并且返回起始點，路徑的走法有四種：

①廣播方式：S→A→S→B→S，即從S點出發到A，返回S，再從S點到B，返回S。

②往返方式：S→A→B→A→S，由S點出發，經過所有點A、B，再沿路返回。

③往返方式：S→B→A→B→S，由S點出發，經過所有點B、A，再沿路返回。

④繞行遍歷方式：S→A→B→S，環繞一周，遍

歷所有點，回到起始點。

表1求出了每種走法的距離及繞行貢獻值。根據三角形兩邊之和大于第三邊，可知第四種走法（繞行遍歷方式）是最短路徑，是最佳走法。假設把前三種走法與第四種走法的距離差稱為繞行貢獻值，繞行貢獻值越大，越值得繞行，這是本算法的一個核心思想。

此外，還要根據S點的夾角K來判斷采用廣播方式、往返方式還是繞行遍歷方式。當S點的夾角K為銳角，才采用繞行遍歷，鈍角則不繞行。

1.2? 貪婪思想

本算法中，先要計算出最短距離矩陣SM、繞行貢獻值矩陣RX。RX值根據篩選公式篩選出來后形成隊列，并按降序存放到JXDL隊列中，再逐條路徑從JXDL堆棧中出棧，進入累加堆棧，累加路程值及重量值，一旦路程累加值超過限程值、重量累加值超過限重值就出棧，剔除剛進棧的路徑，在網絡圖上按照貪婪思想連接已經出棧的路徑，形成一條回程路徑。

1.3? 靠近原則

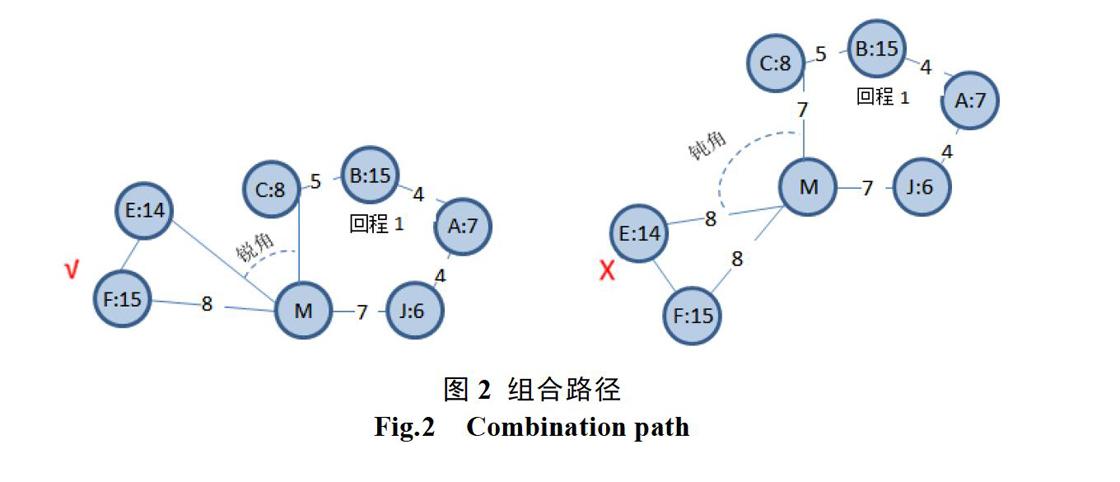
在組成回程時，根據收送貨點是否靠近來組合回路，把相對較遠的路徑推后處理。是否靠近采用模糊神經網絡來處理，如圖2所示，假設E點與組成的回程成銳角時，可以把該地點加入回程，如果是鈍角，則考慮和后面的回程組成回路。

2? 多車多點路徑規劃算法的實現

2.1? 多車多點路徑規劃算法的實現流程

多車多點路徑規劃算法具體的實現流程如下：

（1）先從數據庫中讀取各個收送貨地點的經緯度、客戶收送的貨物重量以及車輛載重、車輛最大行程信息。

（2）利用模糊神經網絡根據收貨點與送貨點的遠近進行分區。

（3）利用百度地圖API計算出各個地點的最短路徑，再算出所有路徑的繞行貢獻值。

（4）對繞行貢獻值篩選后形成降序路徑隊列，再出隊，路徑進入累加堆棧，入棧的時候，累加重量值及路程值;一旦路程累加值超過路程值和重量值就出棧，并剔除剛進棧的路徑。

（5）利用貪婪思想根據路徑是否靠近，對路徑作連接處理形成回路。

（6）把規劃好后的結果存儲到數據庫中，并且用百度地圖API顯示出來。

2.2? 多車多點路徑規劃算法的實現

以物流貨車收貨為例，假設現有A至J的10個收貨地點是在同一組，每個地點的貨物重量（kg）為網絡圖上的結點值，L為起始點S到每個節點的矩離，D為節點間的距離。現有兩種貨車，分別是載重30 kg與50 kg，且貨車一次行駛路程為40公里以內，圖中的邊權為路程（公里）。

（1）收送貨地點進行分區

根據收貨點與送貨點是否靠近進行分區，如果靠近，則把它們歸為一類區，如果不靠近，則把收貨點歸成另外一類區，送貨點歸成第三類區。對于兩點之間是否靠近的判斷，則可以訓練神經網絡來處理。接下來對第一類的客戶點進行分組，使用背包問題的解決方法進行分組：假設有n個客戶點，客戶點j要收貨或送貨的貨物重量為wj（收貨時wj為正值，送貨時wj為負值），價格為pj（pj都為1，因為貨物價格與路徑規劃無相關）。車輛所能承受的最大重量為W。如果限定每種貨物只能選擇0個或1個，用xj表示，使得。

（2）計算最短距離矩陣SM

在數據庫中得到這些地點的經緯度、車輛載重和行程后，利用百度地圖API算出所有結點間的最短路徑，現把收送貨點地圖（圖3）抽象成網絡圖（圖4）。結合百度地圖API和Floyd 算法[8]計算出網絡圖中S起點到各收貨點、收貨點與收貨點的距離，得出收貨線路最短距離矩陣SM（圖5）。

（3）計算繞行貢獻值RX

計算完各結點間最短路徑之后，接下來就要求出哪一條路徑最適合繞行，根據繞行遍歷思想，用繞行公式RX（i，j）=SM（i，0）+SM（j–1，0）–SM（i，j）求出繞行貢獻值[9]（圖6），繞行貢獻值越大，路徑越短，越值得繞行。

（4）對繞行值RX進行篩選

每組成一個回程，則對第二類客戶點與現有的回程作是否靠近的判斷，如果靠近的話，則用插入路徑方法，插入經過此客戶點的路徑。重復此操作，直到所有結點訪問完畢。這樣根據繞行思想和貪婪思想，逐步組合好了規劃路徑，最后通過百度地圖API把這些路徑顯示在地圖上。

3? 結語

本算法是針對多輛車到多個地點的最短路徑問題，在算法中利用神經網絡對地點按遠近進行分區，利用百度地圖API計算出各個地點的最短路徑，根據繞行遍歷思想算出所有路徑的繞行貢獻值，再用貪婪思想把路徑組合起來，最后把規劃好后的結果存儲到數據庫中，并且用百度地圖API顯示出來，使得在物流配送中能夠滿足車輛不超重、不超程并規劃回程的路徑最短。該算法已用在物流企業的多車多點智能路徑規劃云平臺，也可以廣泛應用在物流企業、公交路線規劃、旅游規劃、無人駕駛等各個行業。

參考文獻

[1]鈕亮， 張寶友. 基于云計算求解城市物流配送最短路徑研究[J]. 科技通報， 2015（5）： 184-188.

[2]李晶， 閆軍. 基于Dijkstra算法和Floyd算法的物流運輸最短路徑研究[J]. 科技信息， 2012（2）： 575-576.

[3]王華. 基于Dijkstra算法的物流配送最短路徑算法研[J]. 計算機與數字工程， 2011（3）： 48-50.

[4]高小芳. 物流配送最優路徑規劃[D]. 福建： 華僑大學， 2016.

[5]葉穎詩， 魏福義， 蔡賢資. 基于并行計算的快速Dijkstra算法研究[J]. 計算機工程與應用， 2019， 7.

[6]吳海峰. 最短路徑算法——Dijkstra及Floyd算法[J]. 中國新通信， 2019， 21（02）： 32-33.

[7]魏為民， 陸致靜， 葉語. 一種基于A*算法改進的最短路徑搜索方法[J]. 上海電力學院學報， 2018， 34（02）： 180-184.

[8]張陳翔. 基于Floyd算法的校園導航應用程序開發[J]. 軟件， 2018， 39（4）： 83-85.

[9]駱劍鋒， 陳俞強， 鄭東瀚. 智能交通通信同心游程路由算法[J]. 控制工程， 2016， 6（06）： 975-978.