面向能耗和效率的加工工序排列優化方法研究

高歷 陳冰 肖敏

摘 ?要：以加工時間和能耗雙目標參數的機械加工工序排列優化為應用對象，提出了一種用于優化加工工序排列組合的組合博弈方法。首先建立加工零件模型、工藝流程，搭建了實驗平臺，并根據零件加工過程中各工序所需要的時間、能耗，對零件加工的工序進行了排列組合，在此基礎上，施加合理約束對加工工序組合進行了篩選。基于多目標優化以及博弈理論，采用合作博弈的方法對零件加工工序組合的時間和能耗進行歸一化處理，建立收益函數，按照預設的權重比進行博弈均衡，根據綜合收益選出了加工工序排列組合的最優解。最后通過實例驗證了該優化方法的有效性。

關鍵詞：加工工序排列優化;合作博弈;加工時間;能耗

中圖分類號：TH13 ? ? ?文獻標志碼：A ? ? ? ? 文章編號：2095-2945（2019）35-0001-04

Abstract： In this paper， a combinatorial game method is presented to optimize the permutation and combination of the manufacturing process with the processing time and energy consumption as bi-target parameters. Firstly， the machining part model and process flow are established， and its related experimental platform is built. According to the time and energy-consumption of each process， its machining permutation is cultivated with reasonable constraints applied. Then， these two parameters are normalized with cooperative game method to carry out a profit function， while game is balanced according to the preset weight ratio， and the optimal solution for permutation is eventually figured out under the comprehensive income. Finally， the effectiveness of the optimization is verified by an example.

Keywords： arrangement and combination of manufacturing process; combinatorial game; machining time; energy consumption

引言

當今的全球化市場大環境使得相似機械產品的競爭愈發激烈，從而對產品的快速設計與制造、高柔性、低成本等方面提出了更加嚴格的要求[1]。在具體的產品生產中，出于對時間和能耗等方面的考慮，生產者希望能夠通過在實際生產中通過對工藝以及具體工序的優化，從而減少生產時間和能耗，最終降低成本。但時間、能耗以及可靠性這些指標常常是相互矛盾的，因此生產者需要根據實際生產情況和要求綜合考量時間、能耗以及可靠性等多目標條件要求，最終達成一個盡可能滿足多個設計參考指標要求的方案即博弈均衡。

博弈論是研究決策主體行為發生直接相互作用時候的決策以及這種決策的均衡問題，它主要研究現實中的兩難甚至多難問題，得到一個相對均衡的最優解。通過分析多目標優化的相關理論，發現多目標優化在處理多個目標的矛盾沖突方面與博弈論思想的契合度很高。1991年Rao等[2]率先在機械領域的多目標優化中使用了博弈理論; Lewis等[3]在飛行器設計領域應用了博弈模型;趙健東[4]等將納什均衡應用于挖掘機工裝設計;陳亮[5-6]等根據博弈理論，構建了多目標設計決策模型，并給出了求解方法;Xiao等[7]基于納什均衡，針對多目標、多學科提出了一種非合作博弈的優化方法;Isuamfon等[8]進行了計算機輔助數控刀具路徑能量需求的建模;Li等[9]通過經典推銷員TSP模型，采用模擬退火和蜂巢算法對機床加工的時間和能耗的計算方法進行了推導。

本文將多目標參數優化的博弈論方法應用于生產工藝以及具體工序的排列組合問題，針對合作博弈建立對應的模型和求解方式并給出求解過程，最終通過加工生產案例驗證其有效性。

1 多目標優化模型的構建

多目標優化設計是為了處理各個目標之間的關系及其對最終需求的影響。這正與博弈理論局中人和局中人策略的關系相對應，因此采用博弈理論能夠對多目標優化所面臨的兩難或者多難問題建立合理的模型。而合作博弈追求的是整體效益的最大化，而本文主要研究加工時間和能耗的雙目標參數優化問題，需要將時間和能耗兩個指標綜合起來使得整體效益的最大化，這正與合作博弈思想相契合。

2.3 模型求解約束條件

在實際的產品生產與工藝流程規劃過程中，根據對各個需求指標的權重不同，就會使得博弈結果產生不同。

在進行博弈之前，通常需要通過基于實際生產情況和設備等因素進行考量，設定了三個約束條件：

（1）鉆小孔、鉆大孔工序應該分別在銑小孔、銑大孔工序之前;

（2）盡量減少換刀次數;

（3）銑小孔、銑大孔工序盡量與銑小圓槽、銑大圓槽工序相鄰。

3 基于加工案例的多目標參數合作博弈方法驗證

結合前文，基于加工案例的多目標參數合作博弈方法主要步驟如下：

（1）確定加工模型中特征所需的加工時間和能耗;

（2）計算出加工工序的所有排列組合，通過增加合理約束來縮小備選加工工序排列組合方案;

（3）計算出篩選后的加工工藝流程所需的總時間和總能耗;

（4）通過對各個方案總時間和能耗進行歸一化處理，統一量綱，建立收益函數;

（5）按照合作博弈的收益計算公式，計算出各個方案在該種博弈模型下的最終收益，選出最優方案。

為驗證該方法的有效性，現構建一套有多目標參數的加工方案如圖1所示。在圖1中，加工特征為小孔，其余分別為小圓槽、臺階、大孔、大圓槽，其中臺階為事先已加工完成的工序，因此，主要考慮其余工藝的加工順序排列。

本文的加工設備采用一臺數控加工中心，配備φ3鉆頭、φ3銑刀、φ7鉆頭、φ6銑刀四把刀具，用來加工圖1中與其尺寸匹配的特征，設定了空載、帶載（切削）以及換刀所需的時間和能耗，其中能耗的計算方法如式（8）所示：

其中E代表加工工序（工步）所需要的能量，q代表每一個加工工序（工步）走刀時每秒消耗的能量，t為加工該工序（工步）所需要的總時間。

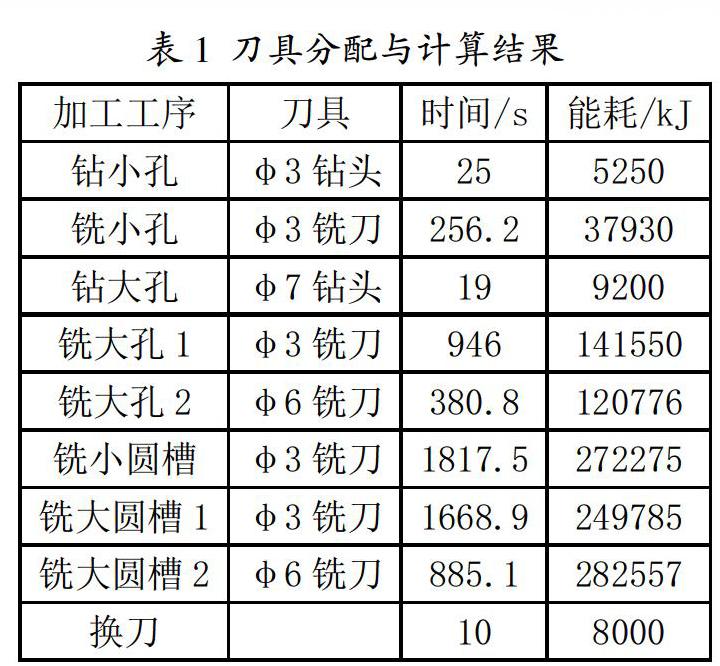
結合式（8）計算方法與圖1中的尺寸數據，計算了不同刀具加工不同特征所需要的時間和能量，最終可得出計算結果與刀具分配方案如表1所示。

結合2.3中所設定的約束，經計算機篩選后，最終得出了滿足約束條件的56種備選加工工序的排列組合。

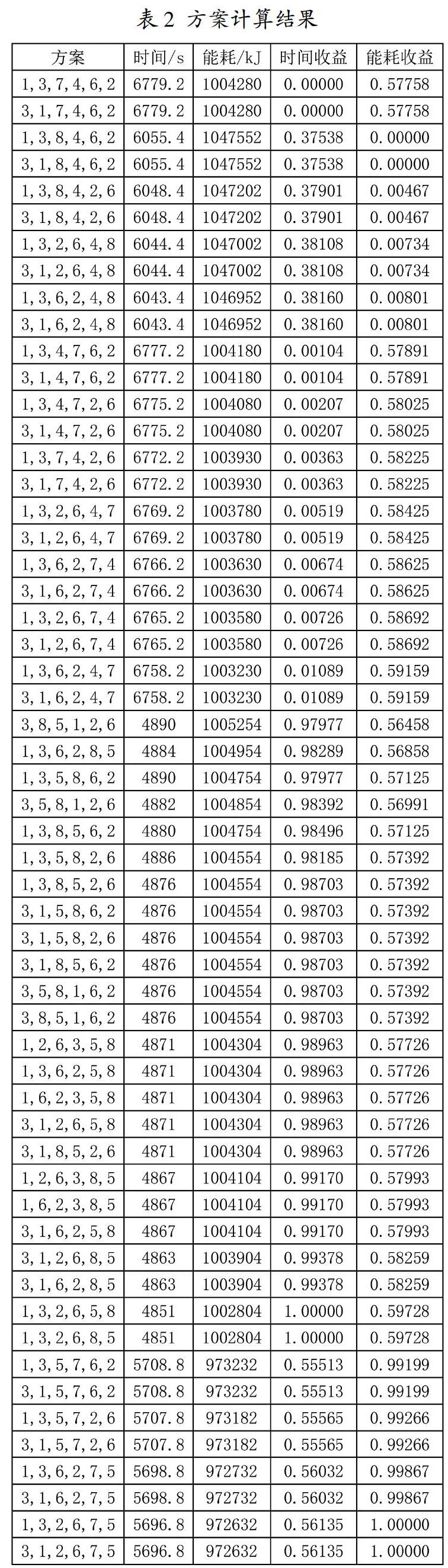
通過對這56種組合的計算，分別得出其所需要的總時間和總能耗，其計算結果如表2第2、3列所示。

由于最終需要綜合考慮時間和能耗需求對方案選擇的綜合影響，因此需要通過博弈相關理論先對其進歸一化處理。時間能耗均對加工工序排列有負向作用，因此應取最小值為最優值。根據式（3），可計算出歸一化處理的時間收益和能耗收益，其結果如表2第4、5列所示。將鉆小孔、銑小孔、鉆大孔、銑大孔1、銑大孔2、銑小圓槽、銑大圓槽1、銑大圓槽2分別編號為1～8，其最終加工方案得出計算結果如表2第1列所示。

歸一化處理之后，根據收益函數計算出其收益，由于本模型只有時間和能耗兩個指標，也只有一個受益人，所以收益函數得出的收益值，就為歸一化處理以后的結果。

合作博弈的目標函數及最后的求解結果， 能較準確地體現各設計需求對產品整體的重要性。由式（4），結合實際加工情況，不妨設時間-工藝重要性系數為0.4，能耗-工藝重要性系數為0.6，其合作博弈收益函數如式（9）所示：

F（X）=[f1（X）]0.4[f2（X）]0.6 （9）

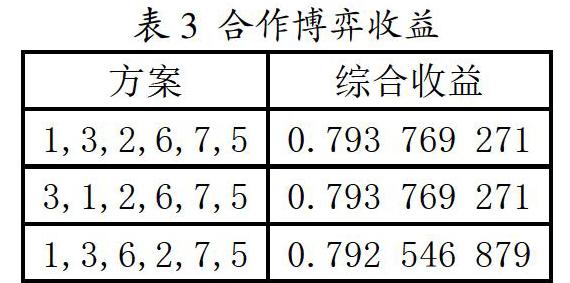
將其最終收益進行計算之后，得出綜合收益結果如表3所示：

其中數字越大，收益越大，故應該優先選擇兩種方案：

方案一：鉆小孔，鉆大孔，銑小孔，銑小圓槽，銑大圓槽1，銑大孔2;

方案二：鉆大孔，鉆小孔，銑小孔，銑小圓槽，銑大圓槽1，銑大孔2。

通過上述模型以及實際案例分析計算可以看出，合作博弈理論在解決加工工藝排列組合的最優解問題上能夠起到很好的效果，所建立的模型也具有一定的科學性和普遍性，也滿足了面向能耗和效率的加工工序排列優化方法研究的需要。

4 結論

本文提出了一種面向能耗和效率的加工工序排列優化方法：針對加工工序優化構建出多目標優化模型，并使用合作博弈對該模型進行求解，到最終通過計算選出最優方案。建立的博弈模型以及求解方法通過加工案例進行驗證，其結果表明該方法基本符合實際情況，對相關問題有指導意義，從而論證了其有效性。

參考文獻：

[1]盧純福，柴灝.機電產品模塊化設計重用的博弈決策[J].浙江工業大學學報，2019，47（04）：406-410.

[2]Rao S S， and Freiheit， T I. A Modified Game Theory Approach to Multiobjective Optimization. ASME[J]. J. Mech. Des. 1991，113（3）：286-291.

[3]Lewis K ， Mistree F. Collaborative， Sequential， and Isolated Decisions in Design[J]. Journal of Mechanical Design， 1998， 120（4）：643-652.

[4]趙健冬，邱清盈，馮培恩.基于Nash均衡的多學科設計優化求解方法[J].農業機械學報，2008（01）：126-128.

[5]陳亮，黃亞慶，劉丹.基于博弈分析的產品多目標設計問題的求解方法[J].中國工程機械學報，2015，13（03）：212-216.

[6]陳亮，李廖平.基于混合博弈的產品多學科柔性設計決策[J].中國機械工程，2017，28（15）：1854-1861.

[7]Mi Xiao，Xinyu Shao，Liang Gao，Zhen Luo. A new methodology for multi-objective multidisciplinary design optimization problems based on game theory[J]. Expert Systems With Applications，2015，42（3）：1602-1612.

[8]Isuamfon F. Edem，Paul T. Mativenga. Modelling of energy demand from computer numerical control （CNC） toolpaths[J]. Journal of Cleaner Production，2017：157.

[9]X.X. Li，W.D. Li，F.Z. He. A multi-granularity NC program optimization approach for energy efficient machining[J]. Advances in Engineering Software，2018：115.