不平衡數據軟子空間聚類算法在臨床醫學中的應用與研究

程鈴鈁 陳黎飛 賴曉燕

摘? 要： 聚類分析是數據挖掘中重要的研究課題，在信息過濾、生物信息學，醫學等領域得到廣泛應用。本課題著重于自上而下的子空間聚類方法，主要原因是當前主要的此型算法都是以K-means或K-modes為基礎的，在均勻效應的影響下，不平衡數據的問題是現有的軟子空間算法不能有效聚類的，所以提出了一種基于劃分的不平衡數據軟子空間聚類新算法。所提算法提高了不平衡數據的聚類精度，在生物信息學和臨床醫學等領域具有一定的理論意義和實際應用價值。

關鍵詞： 聚類分析;子空間聚類;不平衡數據;聚類精度

【Abstract】： Cluster analysis is an important research topic in data mining. It is widely used in information filtering， bioinformatics， medicine and other fields. This topic focuses on the top-down subspace clustering method. The main reason is that the current major algorithms are based on K-means or K-modes. Under the influence of uniform effects， the problem of unbalanced data The existing soft subspace algorithm cannot be effectively clustered， so a new algorithm based on partitioning unbalanced data soft subspace clustering is proposed. The proposed algorithm improves the clustering accuracy of unbalanced data， and has certain theoretical significance and practical application value in the fields of bioinformatics and clinical medicine.

【Key words】： Cluster analysis; Subspace clustering; Unbalanced data; Clustering accuracy

0? 引言

數據挖掘領域的重要研究方法之一是聚類，由于聚類分析具有無監督學習性，所以在眾多領域的得到應用，包括醫學、生物信息、Web日志分析以及金融交易等等。本文是針對在臨床上的應用，我們通常要在手術后最快的預測該病人是否可以正常愈合以便為后續的護理工作提供更好的決策支持。然而，許多臨床藥物產生的數據通常是不平衡的。顯然這些數據是混合數據，這是我們面臨的第一個問題。同時我們還發現在采集的這些混合數據中，不是每個特征對我們最后進行區分病人是否能夠正常愈合都是重要的，其中有的特征是不重要的，這樣一來，我們面對的第二個問題就是特征如何選擇的問題。最后，在實際的臨床應用中，大多數病人都是可以正常愈合的，只有少數的病人不能夠正常愈合，在數據挖掘中，我們將大部分可以正常愈合的人群看做一個類，不能正常愈合的看做另外一個類，很明顯兩大類的數量上具有較大差異，所以我們面對的第三個問題就是類不平衡的問題。 我們將以上3個問題歸納起來稱其為不平衡子空間的聚類的問題。這在臨床醫學應用中是非常有意義的。

子空間聚類是可以識別和生成與每個集群類相關聯的一組特征（或屬性）以形成依賴于集群的子空間。目前的子空間算法有兩種：自下而上的和自上而下的方法。自上而下方法是在整個空間范圍為每個候選聚類計算最佳子空間。實際上，這種類型的當前主要算法基于K均值或K-模式。其研究思想是在原本的算法中增加為每個屬性的增加一個特征權重。這構造了目標集群類的軟子空間。 許多實際應用產生的數據通常是不平衡的[2]。 反例對應于那些沒有患病的人，樣本量相對較大; 基于以上內容本文提出了一種“雙加權”方法，稱為 BWIC（ Bi- Weighting for Imbalanced data Clustering）不平衡數據軟聚類算法。

1? 國內外研究動態

20世紀30年代，Driver 和 Kroeber 第一次提出聚類分析的思想，并將其運用到人類學的研究領域。在之后的幾年，Robert Tryon在心理學領域繼續使用了聚類分析。在接下來的70年中，聚類分析方法已被廣泛開發并應用于許多領域。新提出的算法對低維空間數據集的聚類具有良好的效果。隨著信息時代快節奏的發展，人們更多的開始研究互聯網、人臉文檔等高維數據，這個時候大家發現傳統的聚類算法已經沒有辦法較好的處理這些數據了。Aggarwal在1998年第一次提出子空間聚類之后，闡述了高維數據的尺寸冗余，局部相關性和稀疏性[1]。

在視頻處理、圖形分割等超高維數據問題方面，可惜的是子空間聚類不能給我們較好的結果。但是，對于處理高維數據有較好的效果主要是由于其算法的目標函數都是在歐氏距離度量的基礎上展開研究的。2009年，一種基于自表示模型的稀疏子空間聚類子空間聚類算法誕生了，在之后自適應的k-means 型軟子空間聚類算法出現了，它是由陳黎飛等提出的。次算法需要首先設置一些全局的關鍵參數，在沒有考慮子空間優化問題前提下，通過新的軟子空間聚類優化目標函數最小化了子空間的簇內緊湊度，同時最大化了每個簇類所在的投影子空間[3]。

2? 相關工作

雙加權方法可以為每個群集提供反映其重要性的權重，賦予各個屬性一個特征權重，用來衡量聚類和測量屬性之間的相關性。另一方面，實際數據通常與不同類型的屬性混合，例如數字和分類。導致他們對這兩個重量的“不平衡”貢獻。與K-Means軟子空間算法相比較，該算法提高了不平衡數據的聚類精度。我們可以在手術后最快的預測該病人是否可以正常愈合以便為后續的護理工作提供更好的決策支持。

2.1? 屬性平衡的距離度量

3? 數據集和實驗設置

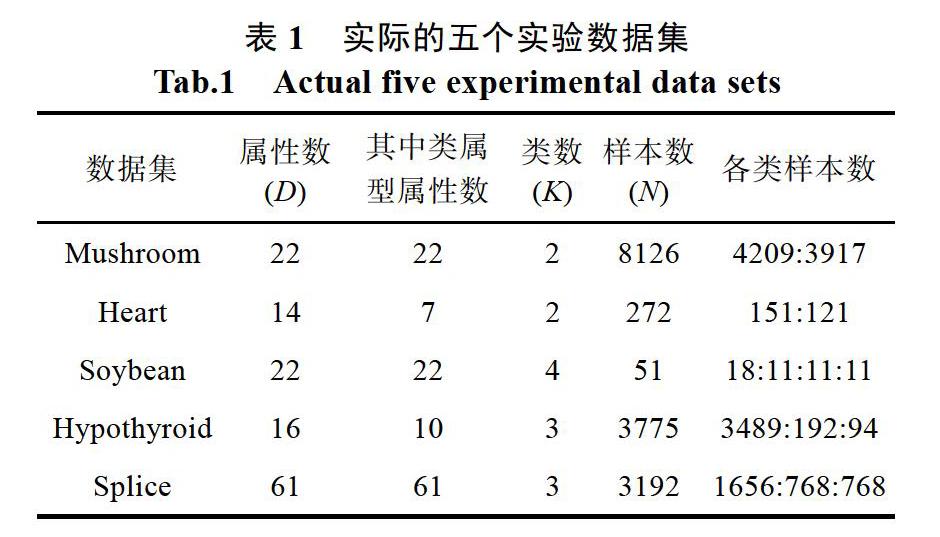
該實驗使用了五個常用的UCI數據集，表1中的Hypothyroid（甲狀腺功能低下者）、Heart（心臟疾病數據）是由數值型數據和類屬型數據混合組成的，而其他的三個數據集單純只含有類屬型屬性，首先前提對所有數據中的所有數值型屬性都預先做了[0，1]規范化處理。此次實驗是對各種算法聚類復雜類型數據的性能的驗證。

所有樣本數據都含“不平衡”的性質，由表1看到，甲狀腺功能低下者Hypothyroid的數據可以分為三組，分別是Hyperfunction超功能、Normal正常和Subnormal次正常表示），最多數據的一組有3489個樣本，而最小的只有94個對象。再有Soybean數據中包含10個樣本數據的有3組，然而第4各組卻有18個樣本，分別用D1～D4表示。還有數據集Splice里的每個對象，都是61個核苷酸序列（位點編號從-30到+ 30），將其分為三組：EI、IE和Neither，對象數分別為768、768和1656;

另外兩組數據集Mushroom、Heart中，盡管各組樣本個數較接近，但卻有明顯的正負例子的區別，Heart數據集可分為“Presence（有心臟疾病）”和Absence（無心臟疾病）”兩種，Mushroom分為“Edible（可食用蘑菇）”和“Poisonous（有毒蘑菇）”兩種。使用這些數據集的原因就是，在實際的臨床應用中，許多臨床藥物產生的數據通常是不平衡的。由于這些數據是混合數據所以實驗數據集這樣安排就是為了解決面臨的第一個問題。同時還解決了前文中提出的第三個問題，實際臨床實驗中，大多數病人都是可以正常愈合的，只有少數的病人不能夠正常愈合，在數據挖掘中，我們將大部分可以正常愈合的人群看做一個類，不能正常愈合的看做另外一個類，很明顯兩大類的數量上具有較大差異。

該實驗過程中使用聚類類屬型數據的K-Modes算法[8-9]（以下簡稱為KM）為基準算法。為了增加對比性，另外選用一種較新的KM改進型算法：基于互補熵的特征加權重KM算法（以下簡稱為WKM），作為對比算法。

3.1? 聚類結果

通過調用BWIC算法聚類每個數據集各20次，分別根據式（9）計算反映結果質量的Silhouette值，再計算平均的Silhouette值。實驗結果表明（見表2）BWIC算法在五個數據集中都取得了較好的聚類結果。由于使用了局部特征加權技術，WKM算法表現出比傳統的KM算法更高的性能。表2也顯示，WKP算法的性能多數情況勝過MKP，其部分原因在于WKP使用了（全局）特征加權技術[7]，可以在聚類過程中識別各屬性對簇類的重要性，進行子空間聚類。相較而言，由于在特征加權基礎上增加了簇類權重的識別功能，BWIC算法的聚類結果顯得更為準確，尤其在樣本分布顯著不平衡的Splice和Hypothyroid數據集上，例如，在Splice數據集上，BWIC算法的平均MacroF1指標和MicroF1指標都超出對比算法近50%。

3.2? 權重計算結果

為檢驗BWIC算法“雙加權”方法的性能，從表3可以得出BWIC算法在每個數據集學習得到的簇類權重。從表中不難發現，輸出的權重值與簇的重要性相關，這樣一來就解決了我們在文中前面提到的第二個特征如何選擇的問題，因為在實際的臨床實驗中，采集的這些混合數據中，不是每個特征對我們最后進行區分病人是否能夠正常愈合都是重要的，其中有的特征是不重要的，有的特征是重要的。

通過3種混合型數據聚類算法BWIC、WKP和MKP在兩個約簡數據集上的聚類性能指標值來看，表中的符號↓表示指標值下降的情況。如表所示， MacroF1和MicroF1兩個指標值都出現了不同程度的下降。

以上結果表明，BWIC算法的“雙加權”可以得到較為準確的結果，尤其是在不平衡數據子空間聚類時[11]。

4? 結論

本文通過提出的新的算法-雙加權方法，即給予每個簇一個反映其重要性的權重（簇權重（cluster- weight）），為衡量屬性與簇類之間的相關性，給予我們每個屬性一個特征權重（feature-weight）。另一方面，現實生活中的數據不可能是單一類型的，而是由數值型和類屬型不同類型的屬性混合組成的，導致它們對兩種權重產生“不平衡”的貢獻。依據在實際應用數據集上進行了實驗，結果表明提出的新算法能夠為不平衡數據中的簇類學習提供更準確的軟子空間;與現有的軟子空間算法相比，新提出的BWIC算法提高了不平衡數據的聚類精度，我們可以在手術后最快的預測該病人是否可以正常愈合以便為后續的護理工作提供更好的決策支持，未來不僅可以在臨床上得到廣泛的應用，在其他的病種分析中也可以得到應用，這將是非常有意義的。

參考文獻

[1]AGGRAWAL C C， Data mining： The textbook， Springer， 2015.

[2]陳黎飛， 郭躬德， 姜青山， 自適應的軟子空間聚類算法， 軟件學報， 21（10）： 2513-2523， 2010.

[3]HUANG J Z， NG M K， RONG H， LI Z， Automated variable weighting in k-means type clustering [J]. IEEE Transactions

on Pattern Analysis and Machine Intelligence， 27（5）： 657- 668， 2005.

[4]CHEN L， WANG S， WANG K， ZHU J， Soft subspace clustering of categorical data with probabilistic distance[J]. Pattern Recognition， 51： 322-332， 2016.

[5]CAO F， JIANG J， LI D， ZHAO X. A weighting k-modes algorithm for subspace clustering of categorical data [J]. Neurocomputing， 108： 23-30， 2013.

[6]MACQUEEN J. Some methods for classification and analysis of multivariate observation[C]//Proceedings of the 5th Berkley Symposium on Mathematical Statistics and Probability， Berkeley： University of California Press， 1967： 281-297.

[7]HUANG Z， NG M. A note on k-modes clustering[J]. Journal of Classification， 20（2）： 257-261， 2003.

[8]李仁侃， 葉東毅. 粗糙K-Modes聚類算法[J]. 計算機應用， 31（1）： 97-100， 2011.

[9]梁吉業， 白亮， 曹付元. 基于新的距離度量的K-Modes 聚類算法[J]. 計算機研究與發展， 47（10）： 1749-1755， 2010.

[10]ZHOU K， YANG S. Exploring the uniform effect of FCM clustering： A data distribution perspective [J]. Knowledge- Based Systems， 96： 76-83， 2016.

[11]HE H， GARCIA E A. Learning from Imbalanced Data[J]. IEEE Transactions on Knowledge and Data Engineering， 21（9）： 1263-1284， 2009.