空時碼不對稱調制方法研究

丁義

摘? 要： 提出了空時編碼不對稱調制方案。軟件分析了比特交織空時編碼調制系統在Rayleigh衰落信道下的成對錯誤概率上界。對于常用的幾種映射方案，采用不對稱調制星座圖，可以增大漢明距離為1的調制符號間的最小歐氏距離，從而提高系統的編碼增益和分集增益，降低成對錯誤概率的上界。理論分析和仿真結果表明，不對稱調制星座圖改善了比特交織空時編碼調制系統在Rayleigh信道下的性能，并且沒有犧牲頻譜效率和增加系統復雜性的代價。

關鍵詞： 比特交織;編碼;調制;不對稱調制;符號映射

【Abstract】： The asymmetric modulation scheme o space-time coded modulation was proposed. The upper pairwise error possibility was analyzed in bit-interleaved space-time coded modulation （BI-STCM） system under Rayleigh fading channels. The minimum Euclidean distance between symbols with hamming distance one can be increased in asymmetric constellation for several ordinary symbol mapping schemes. So the coding and diversity gain can be obtained and the upper pairwise error possibility decreased. Theoretical analysis and simulation results show that asymmetric modulation scheme can greatly improve the performance of BI-STCM under Rayleigh fading channels， with no price of sacrifice the frequency efficiency and increase the complication of the system.

【Key words】： Bit interleaved; Coding; modulation; Asymmetric modulation; Symbol mapping

0? 引言

空時編碼作為一種聯合考慮發射分集、編碼和調制的信道編碼技術，由于其優良的性能，近年來很多學者將比特交織編碼調制（BICM）與空時分集技術相結合，提出了比特交織空時編碼調制（BI-STCM）[1-4]，極大地提高了系統的分集增益、編碼增益和抗衰落性能。文獻[5]對該系統的性能限進行了研究;文獻[6]研究了該系統的容量問題;文獻[7]通過理論錯誤門限的分析，得出迭代時應采用集分割（SP）映射而不是Gray映射的結論;文獻[8，9]分析了BI-STCM的性能限，并對其最優星座映射問題進行了研究。

本文將星座旋轉進一步引入到比特交織空時編碼調制系統中，形成不對稱調制星座。首先分析了影響系統成對錯誤概率上界的參數，詳細討論了星座旋轉對幾種常見映射方案歐氏距離的影響，進而通過不對稱調制，改善信號的距離特性，從而提高系統的編碼增益，降低成對錯誤概率的上界。

1? 系統模型

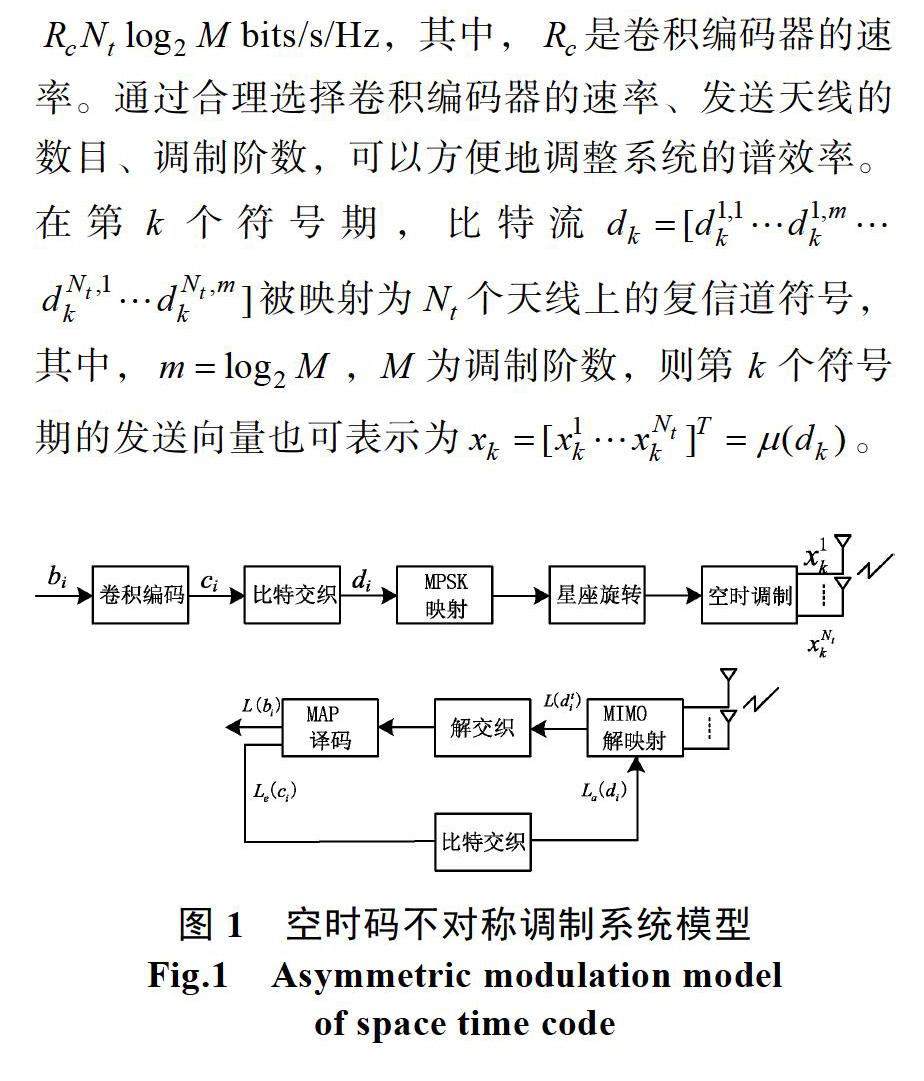
具有根發送天線和根接收天線的比特交織空時編碼不對稱調制系統，如圖1所示。在發送端，信息比特流首先進入卷積編碼器編碼，經比特交織產生比特流，每個比特一組，映射到經星座旋轉形成的不對稱高階相位調制星座圖上，經空時調制后發射出去。系統的譜效率為 bits/s/Hz，其中，是卷積編碼器的速率。通過合理選擇卷積編碼器的速率、發送天線的數目、調制階數，可以方便地調整系統的譜效率。在第個符號期，比特流 被映射為個天線上的復信道符號，其中，，M為調制階數，則第k個符號期的發送向量也可表示為。

接收端采用迭代解碼的方法，首先對來自MIMO信道的接收信號解映射，其中，為信道衰落系數矩陣，為復加性高斯噪聲向量。采用MIMO的軟入軟出后驗概率（MIMO-APP）方法[10]計算每個傳輸比特的軟信息值，求得每一個發送天線上的碼比特的后驗對數似然比，然后，將求得的碼比特的后驗對數似然比依次解交織，送入軟入軟出（SISO）卷積譯碼器，SISO譯碼器按照最大后驗概率（MAP）算法計算信息比特的對數似然比，同時新的對數似然比通過比特交織，反饋回MIMO解映射模塊，作為解映射的外信息，用來進行新一輪的迭代。在最后一輪迭代，通過對的硬判決，獲得信息比特的解碼序列。

由于交織后的信號直接映射到旋轉后的星座點上，因此不對稱調制并沒有增加系統的復雜性。

2? 星座旋轉

對MPSK調制星座的部分或全部星座點旋轉，就形成不對稱調制星座。如前所述，在反饋無誤（EFF）的條件下，要降低比特交織空時編碼調制迭代解碼系統在Rayleigh衰落信道下的成對錯誤概率的上界，必須使系統的分集增益和編碼增益最大化。除設計序列之間的漢明距離使之最大化之外，增大相差一個比特的序列之間的最小平方歐氏距離，即使最大化，就能獲得大的編碼增益。下面討論不對稱調制星座對的影響。

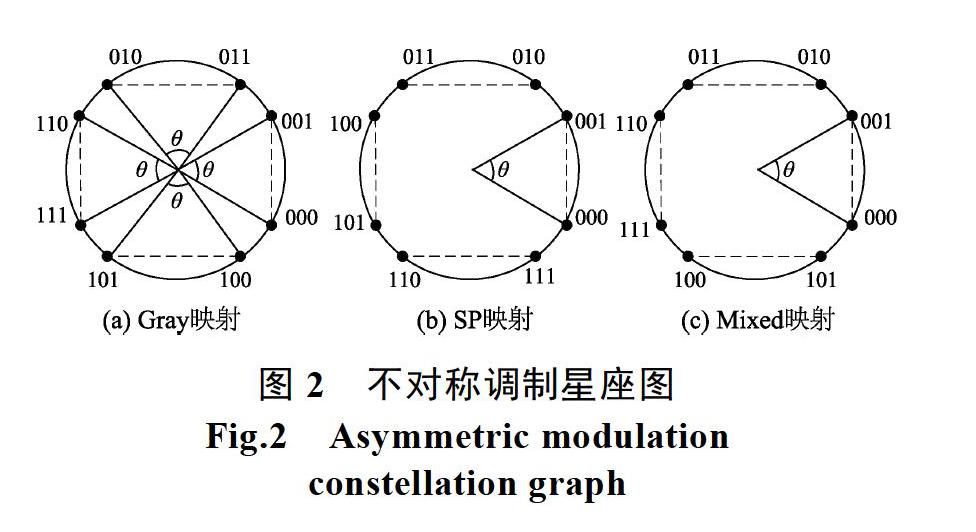
圖2給出了三種映射（Gray、SP、Mixed）的8PSK不對稱調制星座圖。星座的不對稱性用旋轉角表示。對于8PSK調制，當等于時，不對稱調制星座就變成對稱調制星座。

從圖2不難看出，在對稱8PSK星座圖的情況下，在所有三種映射方案中，第一個比特位置或第二個比特位置相差一個比特、且漢明距離為1的調制符號間，都具有較大的歐氏距離，而第三個比特位置相差一個比特、且漢明距離為1的調制符號間歐氏距離最短，因此，它決定了的值，系統的成對錯誤概率上界主要由在第三個比特位置相差一個比特、且漢明距離為1的調制符號間的歐氏距離來決定。圖中虛線分別標出了三種映射在第三個比特位置相差一個比特、且漢明距離為1的符號間的歐氏距離。

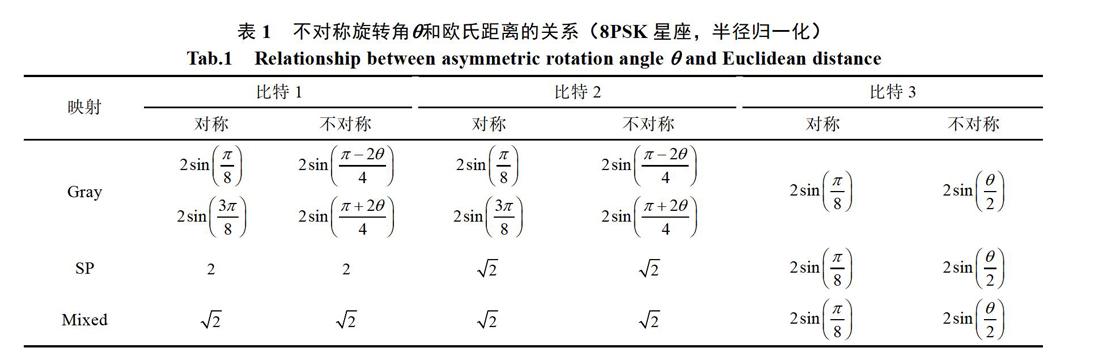
增大角，即采用不對稱調制，能增大在第三個比特位置相差一個比特、且漢明距離為1的符號間的歐氏距離。表1給出了旋轉角和對應的歐氏距離的關系。可以看出，在范圍內，對于Gray映射，增大角后，雖然能增加在第三個比特位置相差一個比特、且漢明距離為1的符號間的歐氏距離，但同時會使第一和第二個比特位置相差一個比特、且漢明距離為1的調制符號間的歐氏距離下降，低于對稱調制星座時的最小歐氏距離。因此，對Gray映射來說，不對稱調制反而使系統的性能下降。

對于SP映射和Mixed映射，增大角后，增加了在第三個比特位置相差一個比特、且漢明距離為1的符號間的歐氏距離，同時，第一和第二個比特位置相差一個比特、且漢明距離為1的調制符號間的歐氏距離保持不變。因此，這兩種映射采用不對稱調制后，能增大最小平方歐氏距離，使系統獲得更高的編碼增益，從而降低系統的成對錯誤概率上界。

3? 軟件仿真結果

仿真參數為：輸入數據塊幀長為260比特;編碼速率為1/3、約束長度為3的卷積碼，生成多項式;長度為780比特的隨機交織器;8PSK調制，旋轉角分別取45（對稱調制）、55、65、75;四發兩收天線系統;迭代次數為8。

圖3給出了BI-STCM系統在Rayleigh快衰落信道下Gray、SP、Mixed三種映射分別采用對稱調制和不對稱調制時的誤幀率性能比較，圖中不對稱旋轉角為55。可以看出，Gray映射采用不對稱調制時的性能下降，這是因為不對稱調制使相差一個比特的Gray映射調制符號之間的最小歐氏距離

變得更小。相比對稱調制，在誤幀率為103時，SP和Mixed映射不對稱調制均能獲得1 dB的信噪比增益。從圖中也可以看出，高信噪比時SP映射的性能優于Mixed映射，這是由于SP映射的距離特性更好，如表1所示。

圖4和圖5分別給出了在Rayleigh快衰落和準靜態衰落信道下，采用Mixed映射時比特交織空時編碼不對稱調制的誤幀率性能。仿真結果表明，當不對稱旋轉角為55時，相比對稱調制方案，在信噪比大于13 dB后，將能獲得明顯的編碼增益。當為65時，快衰落信道下信噪比為13 dB、準靜態衰落信道下信噪比為15 dB時，不對稱調制的性能才與對稱調制時的性能相當，當信噪比更高時，才對系統的性能有所改善。當為75時，不對稱調制使系統的性能惡化，這是因為隨著不對稱旋轉角的

增大，部分星座點歐氏距離變短，使首輪迭代解碼的準確性變差，并通過反饋引起錯誤傳播和影響迭代的收斂性。另外從仿真結果來看，準靜態衰落的誤幀率比較高，這是由于為簡化分析，交織器長度選為780比特，即在幀間無交織，交織僅限制在幀內，從而在準靜態衰落時不用考慮信道的相關性。但不對稱調制對BI-STCM系統性能的影響，在Ray leigh快衰落或準靜態衰落信道下的效果是一致的。

4? 結論

通過分析空時比特交織編碼調制系統的成對錯誤概率上界，可知在Rayleigh快衰落和準靜態衰落信道下，系統的編碼增益和分集增益主要由碼序列的漢明距離和相差一個比特的調制符號間的最小歐氏距離決定。在系統中引入不對稱調制，對于SP映射和Mixed映射，可以增大在特定比特位置上相差一個比特、且漢明距離為1的調制符號間的歐氏距離，而在其它比特位置上相差一個比特、且漢明距離為1的符號間的歐氏距離仍保持不變，從而提高系統的編碼增益，降低成對錯誤概率的上界。

由于沒有準確的先驗信息，不對稱調制星座會使首輪迭代的性能下降。此外，當信噪比較低的時候，很難保證反饋無誤，迭代解碼可能收斂于不正確的值，甚至可能發散。但當信噪比較高時，相比對稱調制，我們提出的不對稱調制方案仍然能獲得一定的性能改善。值得說明的是，這一性能的取得并沒有犧牲頻譜效率和增加系統復雜性的代價。

參考文獻

[1]Zehavi E. 8-PSK trellis codes for a rayleigh channel[J]. IEEE Transaction on Communications， 1992， 40（5）： 873-884.

[2]Caire G， Taricco G and Biglieri E. Bit-interleaved coded modulation[J]. IEEE Trans. Inform. Theory， 1998， 44（5）： 927-945.

[3]Dejonghe A， Jaspar X， Wautelet X， Vandendorpe L. Turbo- equalization considering bit-interleaved turbo-coded modu lation： performance bounds[J]. IEEE International Confer ence on Communications， 2005， 1：521-525.

[4]Young Min Choi， Pil Joong Lee. Analysis of turbo codes with asymmetric modulation[J]. Electronics Letters， 1999， 35（1）： 35-36.

[5]Huang Y H， Ritcey J A. Tight BER bounds for iteratively decoded bit-interleaved space-time coded modulation. IEEE Comm Letters， 2004， vol.8（3）， pp.153-155.

[6]Zhao L， Huber J. Information theoretic analysis of bit interleaved coded space-time modulation. Source and Channel Coding， Erlangen， 2004， pp.143-150.

[7]Hong Z， Hughes B L. Bit-interleaved space-time coded modulation with iterative decoding. IEEE Trans on Wireless Comm， 2004， vol.3（6）， pp.1912-1917.

[8]Huang Y H， Ritcey J A. Optimal constellation labeling for iteratively decoded bit-interleaved space-time coded modulation. IEEE Trans on Info Theory， 2005， vol.51（5）， pp.1865- 1871.

[9]Huang Y， Ritcey J A. Improved 16-QAM constellation labeling for BI-STCM-ID with the Alamouti scheme[J]. IEEE Communication Letter. 2005， 9（2）： 157-159.

[10]Boutros J J， Boixadera F， Lamy， C. Bit-interleaved coded modulations for multiple-inputmultiple-output channels. IEEE Sixth International Symposium on Spread Spectrum Techniques and Applications， 2000， vol.1 pp. 123-126.