鋁合金受壓板件局部屈曲承載力設計方法

袁霖 張其林

摘要：為考察現有鋁合金設計規范預測非焊接受壓板件承載力的準確性，采用殼單元建立單向受壓四邊簡支板、方形截面管柱和十字形截面軸壓柱有限元模型，使用ANSYS計算得到鋁合金板件彈塑性屈曲臨界應力和極限承載力。數值計算結果與理論分析結果對比發現：現有板件彈塑性屈曲應力理論能夠給出鋁合金板件屈曲臨界應力的下限值，誤差較小。中國規范非加勁板件有效厚度預測公式偏保守，因此給出修正的有效厚度預測公式。修正后的非加勁板件有效厚度公式可以提高板件利用率，增強經濟性。

關鍵詞：鋁合金; 板件; 承載力; 有效厚度; 塑性; 屈曲; 局部穩定

中圖分類號：TU512.4; TB115.1

文獻標志碼：B

Design methods for local buckling bearing capacity of

aluminum alloy members under compression

YUAN Lin， ZHANG Qilin

（College of Civil Engineering， Tongji University， Shanghai 200092， China）

Abstract：

To study the accuracy of existing aluminum alloy design standard for predicting the ultimate bearing capacity of non-welded plates under compression， the finite element model of simply supported plate， square-section column and cruciform-section column under axial compression is built using shell elements. The elastic-plastic buckling stress and ultimate bearing capacity of aluminum alloy members are obtained using ANSYS. The comparisons between numerical calculation results and theoretical analysis results show that the existing elastic-plastic buckling stress theories can lead the lower limits of critical buckling stress of aluminum alloy members with small error. The effective thickness predicting formulas of non-stiffened members in Chinese standard are conservative. The improved effective thickness prediction formulas are proposed. The utilization efficiency can be improved by using the suggested formulas on effective thickness of non-stiffened members， which is more economic.

Key words：

aluminum alloy; member; bearing capacity; effective thickness; plasticity; buckling; local stability

收稿日期：2019-07-23

修回日期：2019-08-28

基金項目： 國家自然科學基金（51738009）

作者簡介：

袁霖（1995—），女，河北邯鄲人，碩士研究生，研究方向為鋁合金結構，（E-mail）yuanlin@tongji.edu.cn;

張其林（1962—），男，江蘇海門人，教授，博導，博士，研究方向為鋁合金結構，（E-mail）zhangqilin@tongji.edu.cn

0?引?言

鋁合金具有輕質、高強度的優點，越來越多地被作為承重構件應用于大跨度屋蓋中。[1-3]鋁合金彈性模量小，局部穩定問題較為突出。與鋼材不同，鋁合金材料的應力-應變曲線連續光滑，沒有明顯的屈服平臺，應力超過比例極限后隨即進入應變硬化階段。鋁合金的這一特性對板件的屈曲臨界應力和極限承載力有較大影響。目前，歐洲鋁合金規范（Eurocode 9，以下簡稱“歐洲規范”）[4]和我國《鋁合金結構設計規范》（GB 50429—2007，以下簡稱“中國規范”）[5]均根據材料硬化性能程度的不同分別定義受壓板件全部有效的寬厚比限值和有效厚度公式中的計算因數α1、α2、C1和C2。本文分別應用BLEICH和STOWELL板件彈塑性屈曲理論[6]推導鋁合金板件彈塑性臨界屈曲應力預測公式，并在ANSYS軟件中建立2種鋁合金單板的雙非線性有限元模型，模擬得到板件局部屈曲應力的精確值，然后對22個方形截面管柱和103個等邊十字形截面軸壓柱進行有限元分析，并把數值結果與中國規范、歐洲規范和美國鋁合金設計手冊（Aluminum Design Manual，以下簡稱“美國規范”）[7]的計算結果進行對比，以期為工程設計提供指導。

1?鋁合金板件受壓局部穩定承載力設計?方法簡介

中國規范、歐洲規范和美國規范對板件類型描述對比見表1。同一類型的板件在不同規范中的定義不同，為統一描述，后文以中國規范中的定義進行表述。

1.1?有效厚度法

目前，中國規范、歐洲規范和英國的鋁合金使用規范[8]都允許利用板件的屈曲后強度，并按照有效截面法考慮局部屈曲對構件整體承載力的影響，以便更好地發揮材料性能。考慮到鋁合金擠壓型材截面形狀復雜性和加勁肋形式多樣性，采用有效寬度法[9]進行設計會導致計算繁瑣，因而中國規范沿用歐洲規范中的有效厚度法計算板件承載力。以寬度為b、厚度為t的單向均勻受壓板件為例，有效寬度法的設計思路是，在達到極限承載力時，如果假定板件中間板帶由于受約束較小承受的載荷也較小，大部分載荷由約束較強的板邊承擔，在有效寬度beff?范圍內，板件的應力均達到屈服應力f0.2?，板件的平均應力均為σm，那么板件的極限承載力為

Pu=σmbt=f0.2?beff?t=f0.2?btbeff?b=f0.2?btρc

（1）

式中：ρc為受壓板件有效寬度的Winter公式系數，

ρc=1-0.222

（2）

式中：為板件的換算柔度系數。

按照有效厚度法計算板件承載力的公式為

Pu=σmbt=f0.2?bteff?=f0.2?btteff?t=f0.2?btρc

（3）

式中：teff?為板件的有效厚度。

中國規范中有效厚度折減系數ρc的計算公式沿用Winter公式的形式，只是針對鋁合金硬化類型和板件類型的不同，取略有差異的計算因數α1和α2，即

ρc=tet=α1-

0.22α22

（4）

式中：te為考慮局部屈曲的板件有效厚度。

=f0.2?σcr?=

btf0.2?E12（1-ν2）kπ2

（5）

式中：σcr?為屈曲臨界應力。

對于加勁板件，k=4.0，=0.526btf0.2?E ;對于非加勁板件，k=0.425，=1.61 btf0.2?E。

歐洲規范針對邊緣加勁薄柔板件的有效厚度折減公式為

ρc=C1β/ε-C2（β/ε）2

（6）

式中：β=b/t;ε=250/f0.2?。

取彈性模量E=68 000 MPa，泊松比ν=0.3，將歐洲規范中的有效厚度（式（6））轉化為Winter公式（式（4））形式的等效計算因數α1和α2，見表2。

由表2可以看出，中國規范中的有效厚度公式計算因數α1和α2與歐洲規范中的有效厚度公式轉化后得到的α1和α2非常接近。對于弱硬化合金加勁板件，其應變硬化指數n較大，應變硬化段不明顯，應力-應變曲線接近鋼材的理想彈塑性模型，所以有效厚度法的計算公式與Winter公式相同，即α1=?1.0、α2=1.0。對于強硬化合金，中國規范和歐洲規范都在弱硬化合金計算公式的基礎上乘以0.9的折減因數。

1.2?許用應力法（抗力因數法）

美國規范的設計思路是給出板件允許承受的最大應力FL，該應力與板件的受力形式、寬厚比和材料熱處理方式有關。當板件寬厚比超過S1時，需要考慮局部屈曲對板件極限承載力的影響。采用安全系數nu、ny和na或抗力分項系數y、c和確定板件的極限應力。對于不設加勁肋的加勁板件和非加勁板件，板件的極限應力為

FL=1

y f0.2?，b/t≤S1

cBp-λDpbt，S1

ck2BpE/（λb/t），b/t≥S2

（7）

式中：

S1=（Bp-Fcy?y/c）/λDp;S2=k1Bp/λDp;

Bp、Dp、k1和k2為與材料硬化類型有關的受壓板件屈曲因數;

λ為與板件類型有關的常數，非加勁板件的λ=?5.1，加勁板件的λ=1.6。

1.3?規范中受壓板件全部有效的寬厚比限值

以強硬化鋁合金5083-H321和弱硬化鋁合金6061-T6為例，非比例伸長屈服應力f0.2?分別取266 MPa和245 MPa，彈性模量E=68 000 MPa，泊松比ν=?0.3，計算得到相應受壓板件全部有效的最大寬厚比，見表3。由此可以看出：按照美國規范計算公式確定的寬厚比限值，遠小于中國規范和歐洲規范給出的結果，偏于保守;中國規范和歐洲規范給出的結果基本一致。

2?鋁合金加勁板件屈曲性能和承載力分析

鋁合金材料的應力-應變曲線有應變硬化區段，

且彈性模量只有鋼材的1/3[10]，因此其變形和屈曲問題較為復雜。先從理論上給出采用板件彈塑性屈曲理論推導得到的鋁合金受壓板件屈曲臨界應力計算公式，再建立四邊簡支板單向受壓有限元模型，研究鋁合金板件的屈曲性能。由于均勻受壓的方形截面管柱中各板件的寬厚比相同，所以各板件同時發生屈曲，板件交線將保持直線。假設交線邊為簡支[11]，在有限元軟件中建立方形截面管柱模型進行對比，分析規范中加勁板件設計公式的準確性。

2.1?鋁合金板件塑性屈曲應力

2.1.1?基于BLEICH理論的鋁合金板塑性屈曲應力

BLEICH理論認為，板件在彈塑性階段屈曲時，可假定板件在x方向的抗彎剛度近似按比值Et/E（Et為切線方向彈性模量）減小，x方向對y方向的抗扭剛度按η=Et/E減小，y方向的抗彎剛度保持不變，即假定板件是正交異性的。根據這一假定，可得到板件的彈塑性屈曲微分方程為

Dη4wx4+2η4wx2y2+4wy4+σxt2wx2=0

（8）

采用與彈性屈曲相同的分析方法，可得到彈塑性階段屈曲臨界應力為

σcr，p?=ηkπ2E12（1-ν2）（b/t）2

（9）

基于BLEICH理論，可給出用材料的切線模量Et確定鋁合金板件非彈性屈曲應力σcr，p?的方法。Ramberg-Osgood模型可較好地描述鋁合金材料的應力-應變關系[12]，見式（10），進而可得到任一應力的切線方向彈性模量Et，見式（11），然后用等效切線模量代替彈性模量，可得到式（12）。

ε=σE+0.002σf0.2?n

（10）

Et=σε=11E+0.002nf0.2?σf0.2?n-1

（11）

σcr，p?=Et（σcr，p?）Eσcr，e

（12）

式中：Et（σcr，p?）為材料應力-應變關系中當應力為σcr，p?時對應的切線彈性模量;σcr，e?為板件彈性屈曲臨界應力。在鋁合金板件的彈性屈曲分析中，通常引入板件的換算柔度系數表征板件的彈性屈曲臨界應力σcr，e?與材料屈服強度f0.2?的關系，即

σcr，e?=f0.2?2

（13）

將式（13）代入式（12），得到塑性屈曲應力σcr，p?與屈服強度f0.2?的關系為

σcr，p?=Et f0.2?E2

（14）

引入板件屈曲臨界應力σcr?與屈服強度f0.2?的關系函數χ=σcr?/f0.2?，則有

χ=11+0.002Enf0.2?（χ）n-1?2

（15）

2=χ+0.002Enf0.2?（χ）n-1

（16）

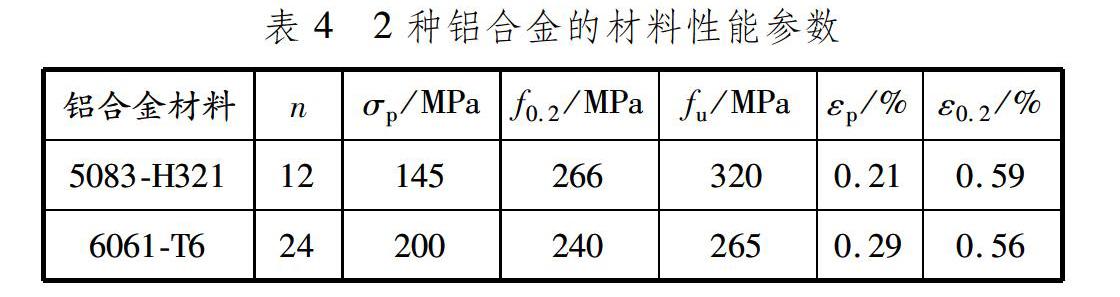
選取2種鋁合金材料5083-H321和6061-T6，分別代表強硬化合金和弱硬化合金，研究材料的應變硬化性能對彈塑性屈曲載荷的影響。2種鋁合金的材料性能參數見表4，其中的σp和εp分別為材料的比例極限應力和比例極限應變。

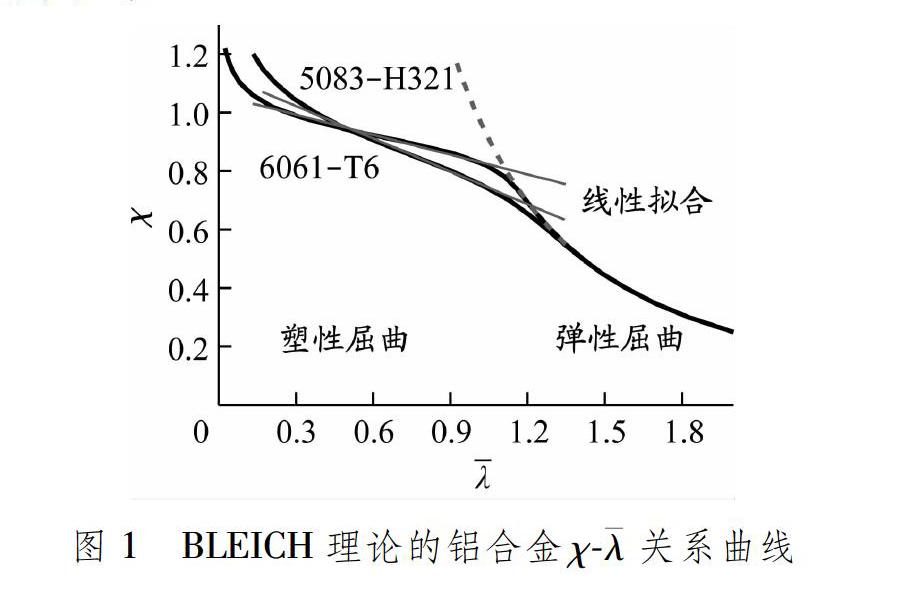
由式（15）可知，當為自變量時，無法得到χ的閉合解，故可先由χ確定，得到兩者的關系曲線，見圖1。

圖1中的χ-關系曲線可以分為2部分：當較大即板件較薄時，板件在彈性階段屈曲;當較小即板件不太薄時，板件在塑性階段屈曲，在這個范圍的塑性屈曲應力與之間沒有閉合解，可由擬合直線近似確定。對于5083-H321鋁合金，

χ=1.13-0.37

（17）

對于6061-T6鋁合金，

χ=1.06-0.23

（18）

由此可得到2種材料基于BLEICH理論的屈曲臨界應力的表達式，對于5083-H321鋁合金，

σcr，t?=（1.13-0.37f0.2?/σcr，e?）f0.2

（19）

對于6061-T6鋁合金，

σcr，t?=（1.06-0.23f0.2?/σcr，e?）f0.2

（20）

2.1.2?基于STOWELL理論的鋁合金板塑性屈曲應力

文獻[13]給出按照STOWELL理論求得的板件彈塑性屈曲應力為

σcr，p?=kmin?π2E12（1-ν2）（b/t）2

（21）

其中：kmin?=2（1+1-ηs），ηs=34（1-Et/Es）。切線模量Et和割線模量Es都隨屈曲應力的變化而變化，因此需要反復試算才能得到彈塑性屈曲應力σcr，p?。基于Ramberg-Osgood模型，可得到

Es=σε=σσE+0.002σf0.2?n

（22）

將式（11）、（22）代入式（21）中，結合χ的定義，可得到關系函數

χ=2+1+31/E+0.002/f0.2?（χ）n-1?1/E+0.002n/f0.2?（χ）n-1?2

（23）

類似地，當為自變量時，無法得到χ的閉合解，故可先由χ確定，得到兩者的關系曲線（見圖2），然后采用線性擬合的方法得到χ與之間的關系式，見式（24）和（26）。

相應地，基于STOWELL理論的塑性屈曲應力表達式見式（25）和（27）。

對于5083-H321鋁合金，

χ=1.210-0.455

（24）

σcr，s?=（1.21-0.46f0.2?/σcr，e?）f0.2

（25）

對于6061-T6鋁合金，

χ=1.079-0.252（26）

σcr，s?=（1.08-0.25f0.2?/σcr，e?）f0.2

（27）

2.2?受壓加勁板件極限承載力分析

采用ANSYS進行數值模擬，用殼單元SHELL181建模，板件厚度取10 mm。對于四邊簡支板，板件長度a取板件寬度b的4倍，邊界條件為四邊簡支，不約束非加載邊的面內位移，見圖3a），其中1為約束，0為不約束。對于方形截面管柱，取截面邊長與四邊簡支板的寬度相等，厚度為10 mm，構件長度取截面高度的3倍，構件軸向網格寬度為20 mm。在上、下端面10 mm的位置設置參考點，施加鉸接約束，見圖3b）[14]，其中1為約束，0為不約束。

在對實際結構進行彈塑性穩定分析時，考慮初始缺陷的影響。按照中國《鋁合金建筑型材 第1部分：基材》（GB/T 5237.1—2008）[15]中的定義，當板件加工精度為超高精級（0.4%）時，缺陷幅值取板寬的0.4%。為力求減小缺陷幅值對屈曲臨界力的影響，本文缺陷采用0.1%板寬的大小。材料采用Ramberg-Osgood模型，取20個應力、應變點構造多折線模型，考慮2種鋁合金材料的性能參數。數值模擬時先對板件進行彈性屈曲分析，把第1階屈曲模態作為初始缺陷形狀施加到模型上，取板件寬度的0.1%作為缺陷幅值進行弧長法分析，得到板件的臨界屈曲應力和極限承載力。

依據應變反向法，當板件承受壓力載荷時，板件兩側表面為相等的壓應力，隨著外部壓力載荷的增大，板件開始出現面外彎曲。[16]由于彎曲拉應力的出現，一側板面的壓應力開始減小，故選取板件屈曲半波上的點代表板面應力分叉的特征點（見圖4）。

當6061-T6鋁合金板件寬度為320 mm時，特征點板面x向壓應力與板面應變關系曲線見圖5。根據該點附近單元的表面應變變化特征，當2條曲線出現分叉時，表明一側板面出現拉應變，板件開始屈曲，該點對應的應力即為屈曲應力。

6061-T6和5083-H321鋁合金板件塑性屈曲臨界應力有限元計算結果與屈曲理論預測值對比分別見表5和6，其中σcr，e?為按照式（2）計算得到的板件彈性屈曲應力，σcr，s?和σcr，t?分別為按照STOWELL屈曲理論和BLEICH屈曲理論計算得到的板件塑性屈曲應力的理論值，σcr，p?為有限元數值模型根據應變分叉法確定的板件彈塑性屈曲應力。由此可以看出，按照BLEICH理論得到的屈曲理論值略小于按照STOWELL理論確定的屈曲理論值，兩者的計算值均小于有限元模擬得到的板件屈曲應力精確解，但誤差很小，故認為可以采用BLEICH理論可以給出板件塑性屈曲臨界應力的下限值，按照BLEICH理論和STOWELL理論均可以較準確地預測鋁合金板件的塑性屈曲應力。

方形截面管柱的具體截面尺寸見表7，其中B為板件寬度，t為板件厚度，L為構件長度。試件編號中的“S5”表示材料為5083-H321，“S6”表示材料為6061-T6，后2位數字為板件的寬厚比。

方形截面管柱屈曲模態云圖和極限承載力下的變形云圖見圖6。ANSYS模擬得到的四邊簡支板極限承載力下的板件平均縱向應力σplate?、方形截面管柱極限承載力下的截面平均軸向應力σsqu?，以及按照中國規范、歐洲規范和美國規范計算公式確定的板件極限應力預測值σGB?、σEC?和σADM?對比見表8。

由此可以看出：由四邊簡支板得到的板件平均縱向應力整體上與方形管柱很接近;中國規范和歐洲規范給出的承載力預測值很接近，與模擬結果的偏差在

10%以內，隨著板件寬厚比增大，2個規范預測的誤差減小;美國規范給出的板件承載力預測值整體上小于中國規范和歐洲規范，偏于保守。

3?鋁合金非加勁板件承載力分析

工程中使用的T形截面板件和工形截面板件的翼緣均為非加勁板件，本文選取等邊十字形截面軸壓柱件進行分析，考察現有規范對于非加勁板件極限承載力計算公式的適用性和準確性。板件厚度均取10 mm，弱硬化合金6061-T6對應的板件寬厚比范圍為5～16（共56個），強硬化合金5083-H321對應的板件寬厚比范圍為4～13（共47個），可涵蓋工程中常用尺寸構件中的非加勁板件寬厚比范圍。材料性能參數、網格劃分與前文的方形截面管柱均相同，十字形截面軸壓柱長度取截面高度的10倍，對板件交線設置鉸接約束，見圖7，其中1為約束，0為不約束。等邊十字形截面軸壓柱屈曲模態和極限承載力下的變形云圖見圖8。

由于篇幅所限，只列出有限元數值模擬和規范對比結果的部分數據，見表9，其中：NGB?、NEC?和NADM?分別為按照中國規范、歐洲規范和美國規范計算得到的截面承載力，NFEM?為有限元模擬結果;

誤差是指與中國規范的誤差;

試件編號中“X5”表示材料為5083-H321，“X6”表示材料為6061-T6，右部的數字為板件的寬厚比。

由表9可以看出，中國規范和歐洲規范會低估

非加勁板件的承載力，有的誤差在10%左右，尤其是當寬厚比增大時，規范結果會更加保守，造成材料不能充分利用。出于經濟性考慮，本文基于有限元模擬結果，提出針對非焊接、非加勁板件有效厚度的建議修正公式，以期在保證安全性的基礎上提高板件的利用率。

中國規范中用于計算非焊接弱硬化合金非加勁板件受壓極限承載力的有效厚度公式為

tet=0.96-0.22×1.02≤1.0

（28）

對應的全部有效板件寬厚比限值[b/t]=6，等效柔度系數限值[]=0.582。

本文給出弱硬化合金有效厚度建議修正公式為

tet=1.1-0.22×1.32≤1.0

（29）

弱硬化合金非加勁板件有限元、中國規范和式（29）計算結果對比見圖9。由此可知，修正公式與有限元數值模擬結果的差值很小，預測較精確。式（29）得到的板件等效柔度系數限值[]=0.679，對應的全部有效的板件寬厚比限值[b/t]=7.01。

中國規范中計算非焊接強硬化合金非加勁板件受壓極限承載力的有效厚度公式為

tet=0.9-0.22×0.92≤1.0

（30）

對應的全部有效板件寬厚比限值[b/t]=7.39，等效柔度系數限值[]=0.512。

本文給出強硬化合金有效厚度修正公式為

tet=0.95-0.22×1.02≤1.0

（31）

式（31）沿用式（4）的形式，在系數確定上保證所有有限元的數據點均落在曲線上方，得到較為安全的有效厚度公式。

強硬化合金非加勁板件有限元、中國規范和式（31）?計算結果對比見圖10。

式（31）對應的板件等效柔度系數限值[]=0.55，?對應全部有效的板件寬厚比限值[b/t]=5.5。

受壓板件全部有效的最大寬厚比[b/t]與材料的非比例伸長應力f0.2?有關。中國規范中引入參數ε=240/f0.2?，在本次分析中：選用6061-T6鋁合金代表弱硬化合金，f0.2?=245 MPa，對應的ε=240/245=0.99，計算得到[b/t]=7.0，當采用其他強度的弱硬化合金時，推導得到對應的最大寬厚比[b/t]=7.0εηk′;選用5083-H321鋁合金代表強硬化合金，f0.2?=266 MPa，對應的ε=240/266=0.95，計算得到[b/t]=5.5，當采用其他強度的弱硬化合金時，推導得到對應的[b/t]=5.8εηk′。公式修正前、后非焊接受壓板件全部有效的最大寬厚比限值見表10。

4?結束語

鋁合金的彈性模量較低，容易發生局部失穩。本文通過理論推導，得到基于BLEICH理論和STOWELL理論、按照Ramberg-Osgood本構模型確定的鋁合金受壓板件彈塑性屈曲臨界應力近似表達式。對比單向受壓的四邊簡支板有限元屈曲分析結果，認為推導得到的表達式能夠較精確地預測板件的彈塑性屈曲臨界應力。對22個等厚度方形截面管柱的數值模擬結果表明，中國規范能夠較精確地預測鋁合金非焊接加勁板件的極限承載力;對103個等邊十字形截面軸壓柱的數值模擬結果表明，中國規范會低估非加勁板件的有效厚度，同時給出優化后的非加勁板件有效厚度計算公式和相應的板件全部有效的最大寬厚比。

參考文獻：

[1]王湛， 段德章， 潘建榮. 鋁合金構件局部穩定問題的研究現狀[J]. 鋼結構， 2017， 32（6）： 1-5. DOI： 10.13206/j.gjg201706001.

[2]常婷. 鋁合金軸心受壓構件局部穩定與相關穩定性能研究[D]. 北京： 清華大學， 2014.

[3]王元清， 常婷， 石永久， 等. 鋁合金軸心受壓構件局部整體相關穩定試驗研究[J]. 土木工程學報， 2016， 49（1）： 14-22. DOI： 10.15951/j.tmgcxb.2016.01.003.

[4]Eurocode9： Design of aluminum structures -?Part 1-1： General structural rules： EN 1999-1-1：2007[S].

[5]鋁合金結構設計規范： GB 50429—2007[S].

[6]BLEICHF. Buckling strength of metal structures[M]. New York： McGraw-Hill， 1952： 105-106.

[7]Aluminiumdesign manual： Specifications & guidelines for aluminum structures： TA690 .A45 2005 F[S/OL].

（2005-12-30）[2019-07-01]. https：//searchworks.stanford.edu/view/5751294

[8]Structuraluse of aluminum： Part 1： Code of practice for design： BS 8118-1[S].

[9]LANDOLFOR， MAZZOLANI F M. Different approaches in design of slender aluminum alloy sections[J]. Thin-Walled Structures， 1997， 27（1）：85-102. DOI： 10.1016/0263-8231（96）00015-8.

[10]季俊， 張其林， 黃政華. 基于有效厚度法的鋁合金構件有效截面特性計算[J]. 計算機輔助工程， 2009， 18（4）： 48-51. DOI： 10.3969/j.issn.1006-0871.2009.04.013.

[11]呂靜， 郭劍， 王彬， 等. 基于ANSYS的角鋼局部屈曲/后屈曲等效分析[J]. 計算機輔助工程， 2013， 22（6）： 74-78. DOI： 10.3969/j.issn.1006-0871.2013.06.014.

[12]Descriptionof stress-strain curves by three parameters： NASA NACA-TN-902[S].

[13]吳亞舸. 鋁合金受壓板件局部屈曲與受彎構件彎扭屈曲承載力研究[D]. 上海： 同濟大學， 2005. DOI： 10.7666/d.w1657626.

[14]常婷， 王元清， 石永久， 等. 鋁合金軸壓構件局部穩定的設計方法分析[J]. 建筑結構， 2015， 45（11）： 32-36. DOI： 10.19701/j.jzjg.2015.11.007.

[15]鋁合金建筑型材： GB/T 5237.1—2008[S].

[16]SOUTHWELLR V. On analysis of experimental observations in problems of elastic stability[J]. Proceedings of Royal Society A： Mathematical， Physical and Engineering Sciences， 1932， 135（828）： 601-616. DOI： 10.1098/rspa.1932.0055.

（編輯?武曉英）