基于漸進法的船舶橫搖非線性阻尼系數識別

孫金偉，邵 萌，邵珠曉，李選群，萬曉正，趙環宇，劉海豐

（1.中國海洋大學工程學院，青島266100；2.山東省海洋工程重點實驗室，青島266100；3.齊魯工業大學（山東省科學院）海洋儀器儀表研究所，青島266001；4.山東省海洋環境監測技術重點實驗室，青島266001）

0 引 言

船舶橫搖阻尼的準確估算是正確預報波浪中橫搖運動的前提。小角度橫搖時，船舶橫搖運動可以用線性方程描述，但當橫搖幅值增大時，必須考慮非線性效應。橫搖非線性主要表現在回復力矩的非線性和阻尼的非線性，很多學者對非線性的阻尼和回復力矩數學模型開展了研究[1-4]。

船舶橫搖回復力矩可由不同階次的奇次多項式函數表示，回復力矩系數可通過與流體靜力學計算得到GZ曲線進行擬合獲得[5]。而對于橫搖阻尼項，目前尚未有完備的理論計算方法，現有的船舶耐波性評估的勢流理論不能預報橫搖運動中由于摩擦、旋渦和流動分離等因素產生的粘性阻尼[6]。基于模型試驗獲得的經驗公式在實際使用中較為方便，但是僅對特定船型適用[7-9]。因此在工程實踐中常用模型試驗的方法來確定船舶橫搖阻尼系數。

最早利用模型試驗進行橫搖阻尼系數估算的學者是Froude（1872）[10]。Wassermann（2016）等[11]對不同的模型試驗技術，包括衰減橫搖試驗和強迫橫搖試驗方法等進行了研究總結。Spouge（1988）[12]對于不同學者提出的各類不同阻尼系數識別方法和結果進行了總結比較，并探討了各種方法的識別精度。Mathisen 和Price（1985）[13]提出了估算衰減橫搖和強迫橫搖試驗阻尼系數的方法，研究發現線性加平方項阻尼模型比線性加立方項阻尼模型具有更好的優越性。Roberts（1985）[5]提出了根據自由橫搖衰減曲線估算非線性橫搖阻尼項的計算方法，該方法適用于小阻尼情形，不限制回復剛度的非線性程度，但遺憾的是作者給出的例子中并沒有考慮強非線性的回復力矩。Chan 等（1995）[14]將徐兆（1985）[15]提出的一種新的漸進法應用于船舶非線性橫搖阻尼系數估算中，該方法適用于大角度橫搖以及強非線性回復力矩，但是其在不同初始橫搖角度下的阻尼系數識別結果存在一定計算誤差，識別精度仍有待提高。李紅霞等（2005）[16]根據衡量耗散的觀點利用橫搖試驗衰減曲線，提出了一種非線性阻尼識別方法，通過算例分析認為二次阻尼模型和三次阻尼模型對船舶橫搖的作用是等效的。馬新謀等（2013）[17]采用李紅霞等提出的能量法，依據兩棲車輛自由橫搖衰減曲線確定了兩棲車輛的非線性阻尼項。馬山等（2012）[6]基于模型試驗的橫搖衰減測量數據，采用能量法進行了船舶橫搖阻尼系數的研究，并通過實驗證實了采用能量法獲取的橫搖阻尼系數結合勢流興波阻尼預報橫搖運動具有較高的精度。

本文基于非線性力學中的漸進法，發展了一種基于橫搖自由衰減數據的阻尼系數識別方法，通過數值仿真和對比研究分析，驗證了該方法的高精度和適用性，最后將該方法應用到船舶橫搖衰減實測數據，識別其非線性阻尼系數，數值模擬結果與試驗數據表現出了較好的一致性。

1 漸進法介紹

對強非線性系統，其運動可由下列微分方程描述

式中：ε為小參數，函數g( x )和f(x,x)滿足如下關系：

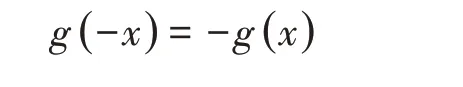
根據攝動理論[18]，（1）式具有如下形式的廣義漸進解

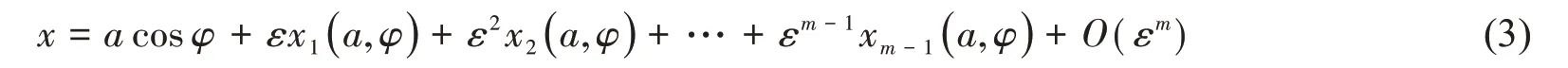
式中：a 是振幅，φ 是相位角，均為時間的緩變函數，x1,x2,…,xm-1是相位角φ 的周期函數，其周期為2π。a和φ由如下微分方程決定：

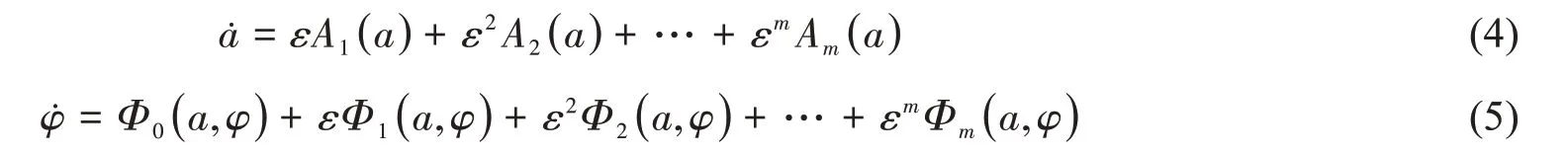
為簡化計算，（1）式的解通常由其一階近似解表示[15]

式中：

因此要求解（6）式，則需要求解（7）式中參數A1( a )，Φ0( a,φ )和Φ1( a,φ )。具體步驟如下：

令ε = 0，則由（7）式可知：a= 0，Φ0( a,φ )= φ。當ε = 0時，（1）式變為

（8）式兩邊同乘以x并積分可得

式中，C是積分常數，且有

假定初始條件為x(0)= a,x( 0 )= 0，則由（9）式可確定C = V(a)。將（6）式代入（9）式中可得

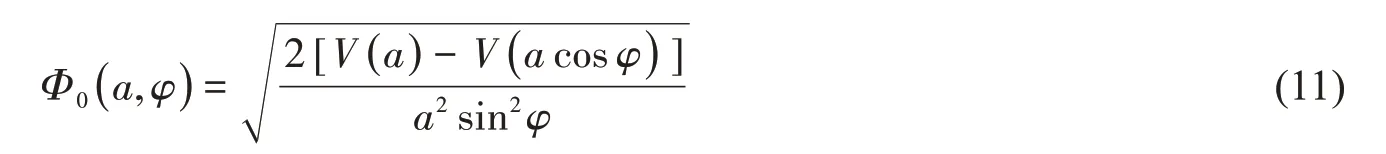
由（6）-（7）式可得

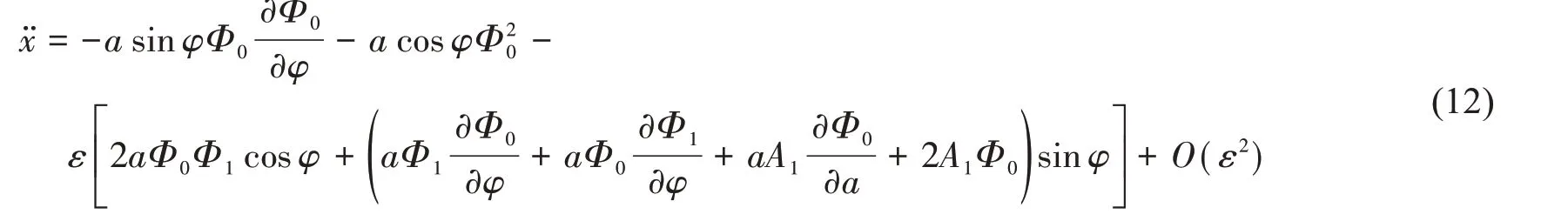
把函數g( x )展開成ε的冪級數

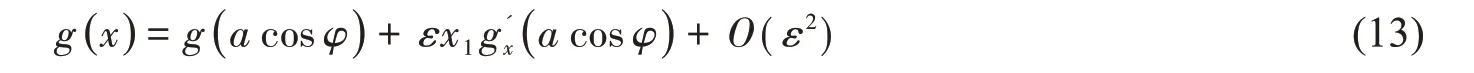
將（12）和（13）式代入（1）式，使等式兩邊ε 項的系數相等，得到

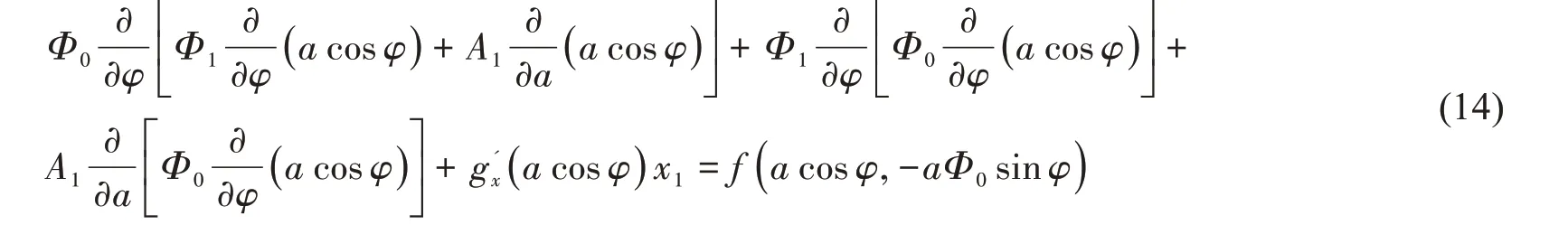
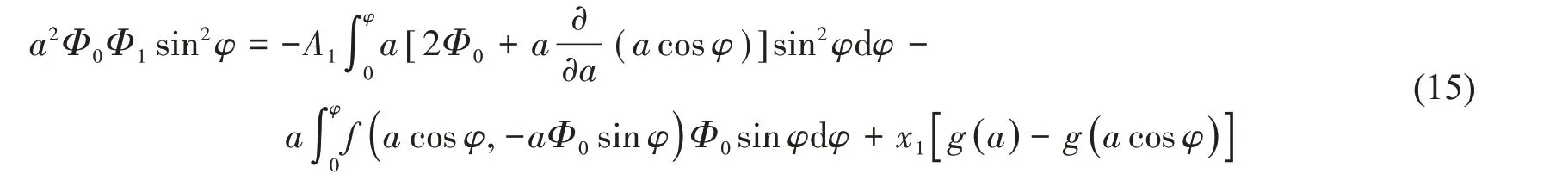
令φ = 2π，可以求出A1表達式

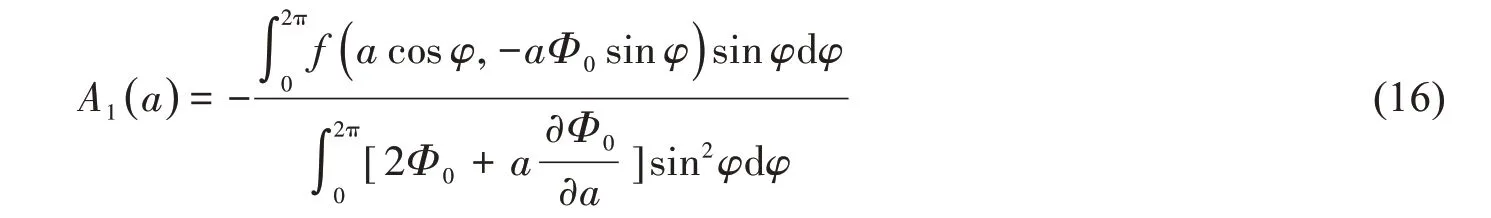
令φ = π，可以求出Φ1表達式。至此，（7）式中的未知項A1( a )，Φ0( a,φ )和Φ1( a,φ )全部求出，于是方程一階近似解的表達式（6）可求出。

2 阻尼系數識別

船舶橫搖非線性阻尼選用如（17）式所示的線性加平方阻尼模型，回復力矩用如（18）式所示的奇次多項式函數表示：

（18）式中的冪次數項j和回復力系數kj可由流體靜力學計算的GZ 曲線進行擬合求得。將（17）式和（18）式代入（1）式，得到船舶橫搖非線性運動方程如下

由（10）式和（18）式可得

將（17）式代入（16）式，可得

式中，

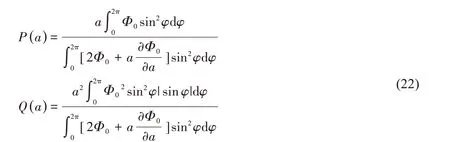
P( a )和Q( a )是幅值a的函數，可以用多項式函數( a )和( a )近似表示：

式中，系數p11，p12，q11和q12可通過最小二乘法進行數據擬合得到。于是（21）式可寫為

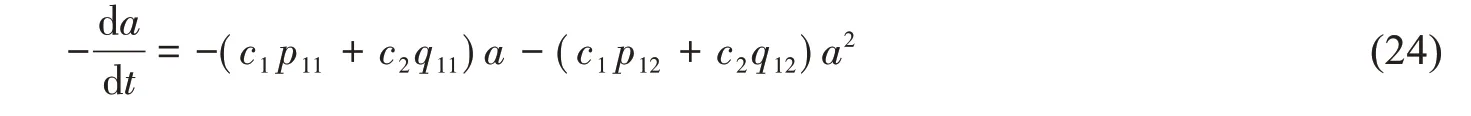
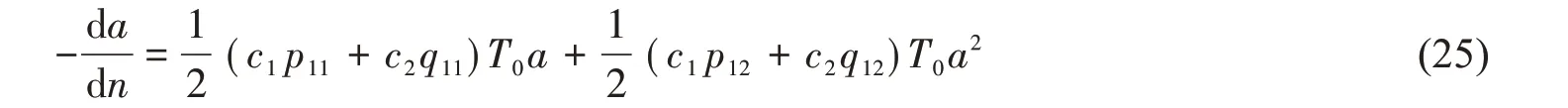
橫搖固有周期T0等于衰減數據的平均周期[13]，可由（26）式確定

式中，x0是初始橫搖角。根據橫搖衰減數據，采用間隔半個周期的橫搖角幅值差與相鄰兩次的平均橫搖角幅值繪制橫搖消滅曲線，對數據進行擬合可得到曲線近似表達式為

由（25）和（27）式可求得阻尼系數c1和c2的估算值：

（28）式中阻尼系數的識別精度與初始橫搖角有關。為提高阻尼系數識別精度，本文進行如下的迭代誤差修正：將（28）式中的阻尼系數初次估算值和代入船舶橫搖運動方程（19）式中，初始條件不變，仍為x( 0 )= x0和x(0)= 0，采用龍格庫塔方法進行數值求解，可仿真生成自由橫搖衰減曲線，求得新的橫搖消滅曲線

同理，再次根據（28）式，可以求得阻尼系數的第二次估算值：

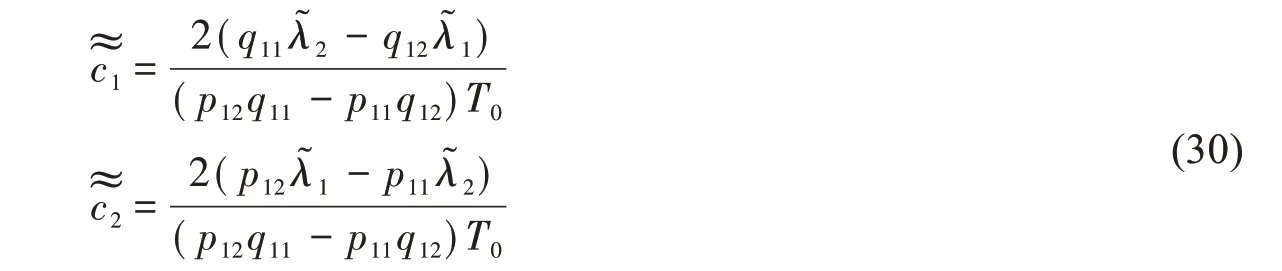
前兩次阻尼系數估算值的相對誤差為：

3 有效性驗證

為驗證本文提出的阻尼系數識別方法的有效性，選用（33）式的橫搖動力學非線性方程作為算例[14]，初始條件x( 0 )=0.3 rad( 0 )= 0。通過數值方法模擬生成自由橫搖衰減曲線，然后用本文方法識別其阻尼系數，并與精確值相比較以驗證方法的有效性。橫搖運動響應采用四階龍格庫塔法求解，時間間隔為0.01s，計算時長為50s。圖1 和圖2 是模擬得到的橫搖衰減曲線及相應的消滅曲線。回復力矩表達式為g( x )= 2.25x - x3，具有強非線性特征，其最大回復力矩對應的橫搖角為0.866 rad，回復力矩曲線如圖3所示。

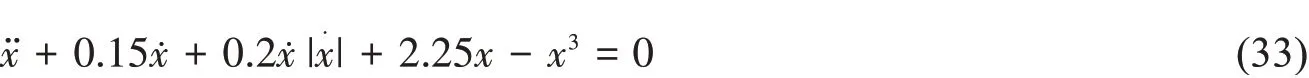
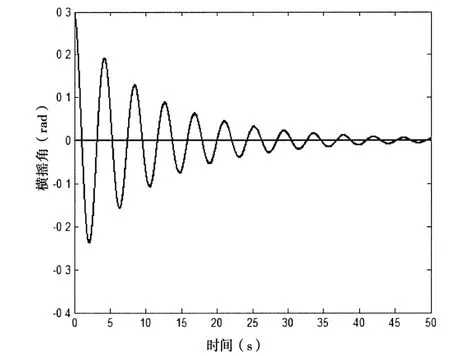
圖1 模擬自由衰減曲線 Fig.1 Simulated free-decay curve

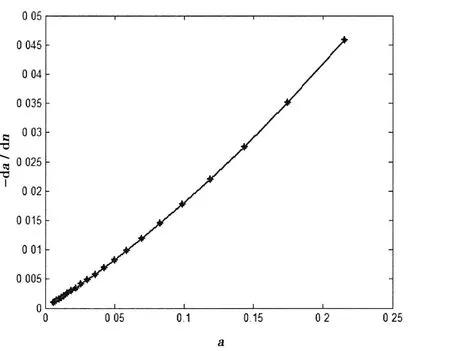
圖2 橫搖消滅曲線Fig.2 Roll extinction curve

根據消滅曲線數據擬合結果，（27）式可寫為

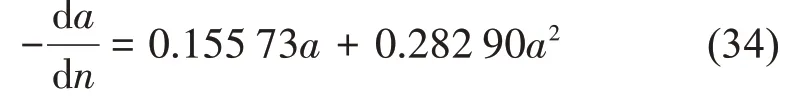
根據（20）式和（11）式計算可得

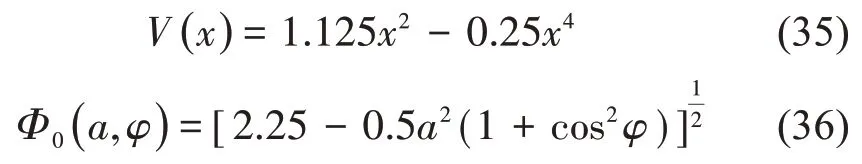
根據（23）式可得

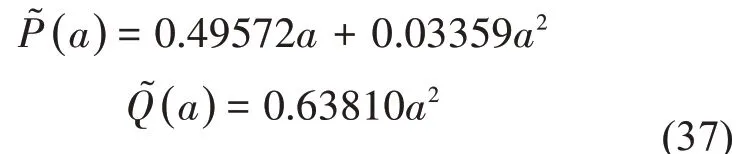
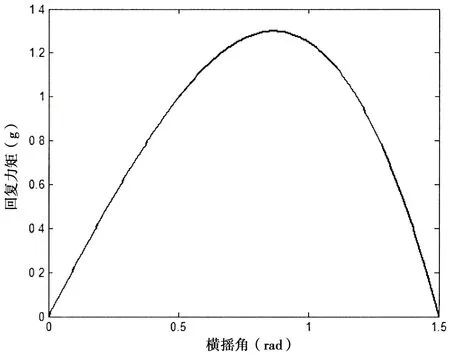
圖3 非線性回復力矩Fig.3 Nonlinear restoring moment

由（26）式可得橫搖衰減運動固有周期T0=4.253 16 s，根據（28）式計算可得到阻尼系數的第一次估算值為= 0.147 83 和= 0.200 70；將和作為新的阻尼系數代入到（33）式中，重復上述計算過程，得到阻尼系數第二次估算值=0.14567和=0.20144，前兩次阻尼系數估算值之間的相對誤差為η1=-1.458 74%和η2=0.367 16%；阻尼系數的第三次估算值=0.143 53和= 0.202 21，后兩次阻尼系數估算值之間的相對誤差為=-1.469 20%和= 0.383 33%。于是，根據（32）式可求得一階和二階阻尼系數的最終估算值c1 =0.150 00和c2= 0.200 00，與（33）式中阻尼系數準確值相等，識別誤差為零。

為考察本文方法的精度，開展不同橫搖角幅值下的參數研究，將船舶橫搖方程的阻尼系數識別結果與采用其他方法得到的估算結果進行對比分析。

采用本文方法對（33）式在不同初始橫搖角時的非線性阻尼系數進行了識別，計算結果見表1，同時將本文中阻尼系數的識別結果和相對誤差等與文獻[14]的計算結果進行了比較，如表2所示。由表1 可知：隨著初始橫搖角的增大，阻尼系數識別質量逐漸變差，相比于一階阻尼項系數而言，二階阻尼項系數識別受初始橫搖角的影響更為敏感，表現在其相對誤差出現時對應的橫搖角更小，且相對誤差值更大。同時由表2 的對比可以看出：無論是對小初始橫搖角還是大初始橫搖角，文獻[14]的阻尼系數識別值均存在相對誤差。而本文方法的識別結果在初始橫搖角不大于0.6 rad 范圍內，均能夠較為精確地識別出一階和二階阻尼系數，識別誤差不大于0.03%；在大初始橫搖角度時，本文阻尼系數識別精度明顯高于文獻[14]，如在最大橫搖角0.866 rad 的初始條件下，本文的一階和二階阻尼系數識別誤差分別為0.26%和0.415%，而文獻[14]給出的阻尼系數識別誤差分別為1.22%和1%，本文方法的一階和二階阻尼系數識別誤差僅為文獻[14]的0.21倍和0.42倍。

表1 不同初始橫搖角下（33）式的阻尼系數識別結果Tab.1 Estimation of damping coefficients from Eq.(33)under different initial roll angles

同時，選取如下船舶橫搖方程進行研究[5]

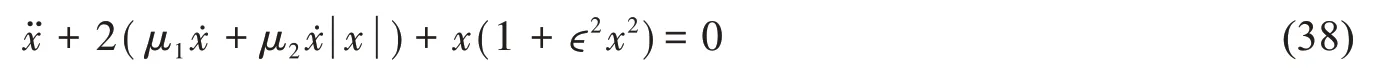
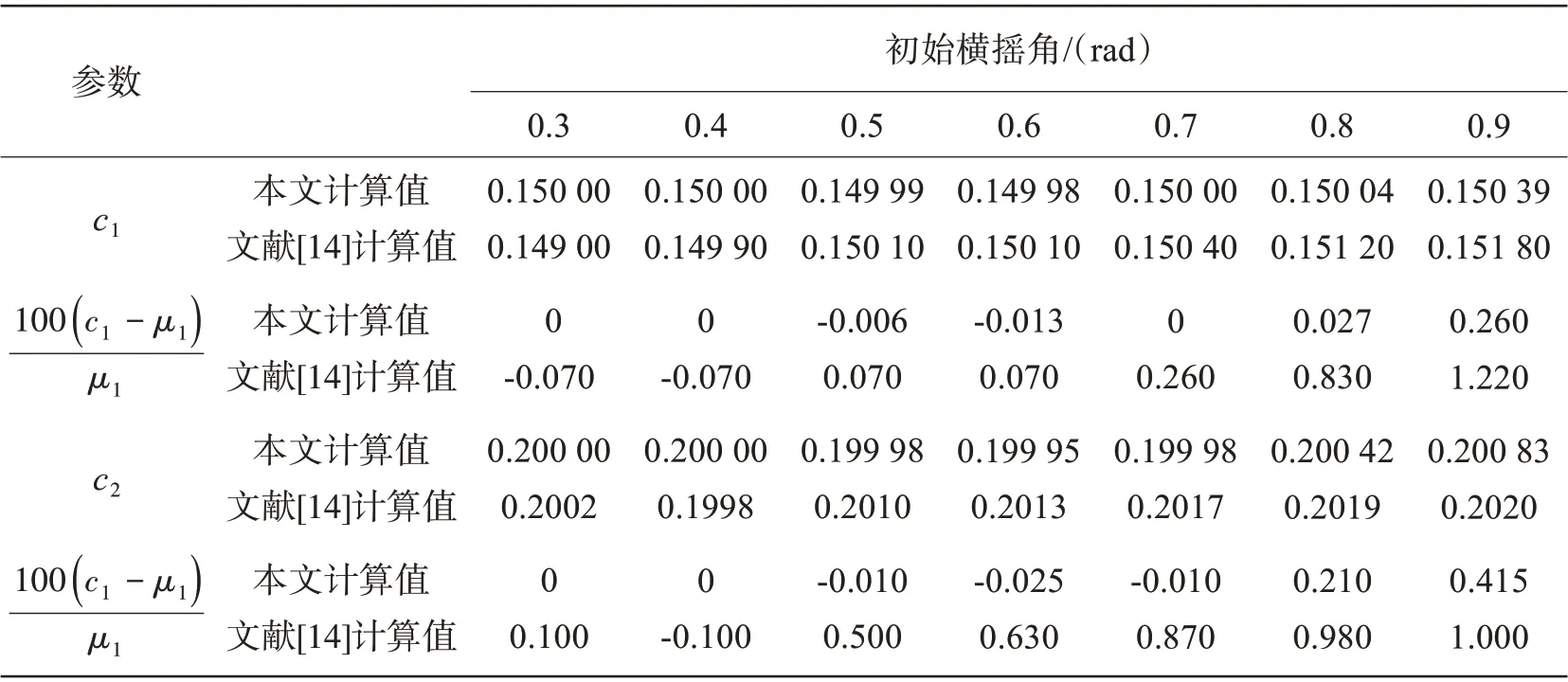
表2 本文識別的阻尼系數與文獻[14]結果比較Tab.2 Comparison of the present work and the results from Ref.[14]

4 實例分析

將本文阻尼系數識別方法應用到實際船舶橫搖衰減數據中。船模試驗得到的橫搖角峰值如表4所示[5]，船模的自搖橫搖周期為2 s，對應實船的船模回復力矩為g( x )= 9.87x + 0.001 974x3。阻尼模型選用線性加二次阻尼模型，于是船舶模型的橫搖運動方程如下：

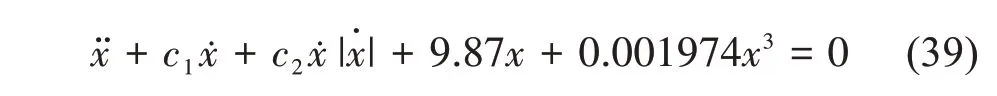
根據回復力矩表達式，可求得Φ0( a,φ )的表達式

計算得到（23）式中擬合系數p11=0.500 0,p12=0,q11=0,q12=1.333 4；由橫搖衰減峰值數據可得到船模的橫搖消滅曲線，進行數據擬合計算得到（27）式中擬合系數λ1= 0.678 4，λ2= 0.073 9。

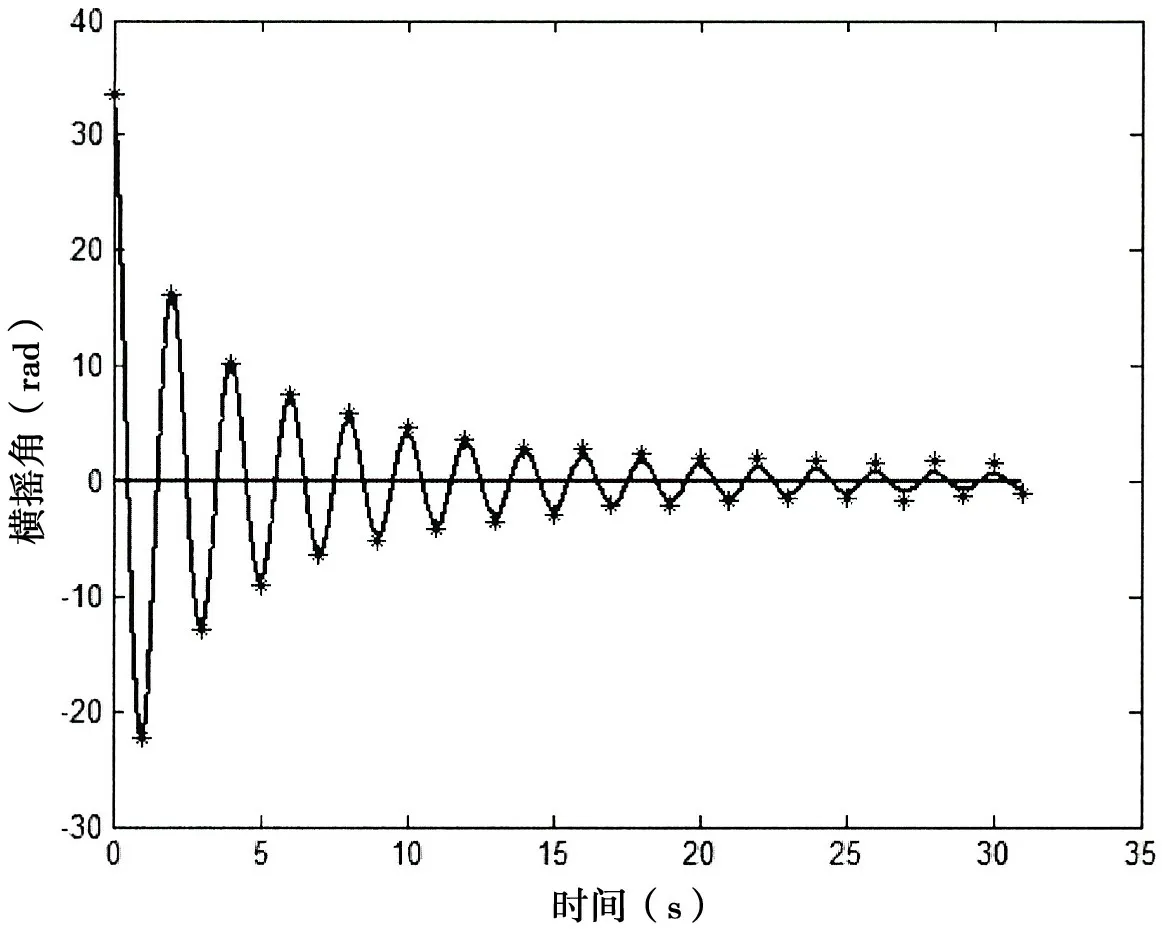
圖4 模擬的自由橫搖衰減曲線和試驗峰值數據比較Fig.4 Comparison of experimental data on free-roll decay motion with the numerically simulated results

根據（28）式，可得阻尼系數c1和c2的第一次估算值= 0.147 9 和= 0.508 8。重復前文所述計算流程，得到阻尼系數最終估算值c1= 0.138 7，c2= 0.528 2。將該阻尼系數代入到（39）式中，通過數值模擬得到自由衰減曲線，并與衰減試驗峰值數據進行比較，對比結果見圖4。由圖4 可知，本文估算得到的橫搖衰減曲線峰值與船模試驗得到的橫搖峰值吻合較好，進一步驗證了本文方法的有效性。

5 結 論

本文基于漸進理論，發展了一種利用試驗衰減曲線進行非線性橫搖阻尼系數識別的方法。通過數值仿真模擬及與已有研究成果的對比分析研究，驗證了本文提出的阻尼系數識別方法的有效性和高精度，最后將該方法應用于實際船舶算例，模擬計算得到的自由衰減結果與試驗數據吻合較好。通過本文的研究，可以得到以下結論：

（1）僅需要自由橫搖衰減曲線峰值數據，利用本文提出的阻尼系數識別方法可精確估算出非線性橫搖阻尼系數；

（2）本文提出的非線性阻尼系數識別方法適用于強非線性的回復力矩情形，回復力矩可以是任意形式奇次多項式函數；

（3）本文提出的非線性阻尼系數識別方法適用于大角度橫搖，且具有較高的識別精度。雖然隨著初始橫搖角幅值的增大，阻尼系數識別質量下降，二階阻尼系數的識別誤差相對更高、出現誤差時對應的初始橫搖角度也更小。但是在最大回復力矩對應的橫搖角范圍內，一階和二階阻尼系數識別的相對誤差仍非常小，在可接受范圍內，特別是在小角度初始橫搖角幅值條件下，阻尼系數的識別誤差接近為零。