半群的帶限度（λ，μ）-雙極值模糊雙理想

王豐效

（喀什大學數學與統計學院，新疆 喀什 844000）

模糊集理論已被廣泛應用于許多領域，作為經典模糊集的推廣，雙極值模糊集、區間值模糊集、直覺模糊集等理論也被應用于許多代數系統，如，群、半群、環、坡代數和 N（2，2，0）代數等[1-4].半群是一類應用廣泛的代數系統，模糊半群理論在許多領域具有重要的作用[5-7].文獻[8]將模糊集應用于半群，研究了半群的幾類模糊理想的特征.謝祥云等[9]的專著中詳細介紹了模糊半群理論.文獻[10-11]分別討論了半群的反模糊子半群和區間值反模糊子半群的特性.文獻[12-13]分別討論了半群的區間值模糊子半群和區間值模糊理想的相關特性. 作為模糊子半群和模糊理想的推廣，帶限度（λ，μ）的模糊子半群和模糊理想被應用于半群等代數系統[14-16]. 本文將雙極值模糊集應用于半群，引入了半群的帶限度（λ，μ）-雙極值模糊雙理想和（λ，μ）-雙極值模糊廣義雙理想的概念，并研究了它們的相關性質，給出了半群的（λ，μ）-雙極值模糊雙理想與模糊雙理想及半群的雙理想的關系.

1 預備知識

定義1[9]設“·”是集合S 的一個二元運算，如果對任意 x、y、z∈S，有

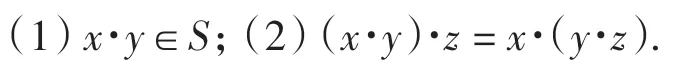
則稱（S，·）為一個半群.為方便，二元運算x·y 簡記為xy.

定義2[9]設S 是一個半群，S 的非空子集T 稱為S 的子半群，如果T2?T.S 的非空子集T 稱為S 的左理想（右理想），如果 ST?T（TS?T）.如果 T 既是 S 的左理想，又是S 的右理想，則稱T 為S 的理想.S 的非空子集T 稱為S 的廣義雙理想，如果TST?T.如果T既是S 的廣義雙理想，又是子半群，則稱T 為S 的雙理想.

定義 3[15]設 0≤α ＜ β≤1. μ 是半群 S 的模糊集，如果對任意 x、y∈S，有 μ（xy）∨α≥μ（x）∧μ（y）∧β，則稱 μ 為 S 的（α，β）-模糊子半群. 如果對任意 x、y、z∈S，有 μ（xyz）∨α≥μ（x）∧μ（z）∧β，則稱 μ 為 S 的（α，β）-模糊廣義雙理想.如果 μ 既是半群 S 的（α，β）-模糊子半群，又是（α，β）-模糊廣義雙理想，則稱μ 為半群 S 的（α，β）-模糊雙理想.

非空集合 X 的雙極值模糊集定義為A=[φ-A，φ+A]，這里 φ+A：X→[0，1]和 φ-A：X→[-1，0]是 X 上的映射.設 A=[φ-A，φ+A]是 X 的雙極值模糊集，記

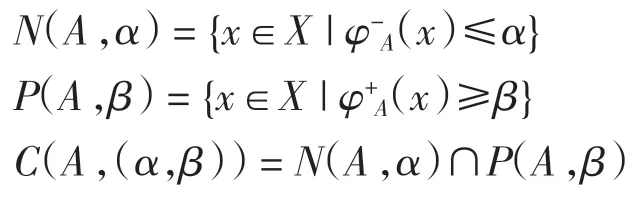
設 A=[φ-A，φ+A]和 B=[φ-B，φ+B]分別是非空集合 X和Y 上的雙極值模糊集，定義A 和B 的直積為A×B=[φ-A×B，φ+A×B]，其中對任意的（x，y）∈X×Y，有

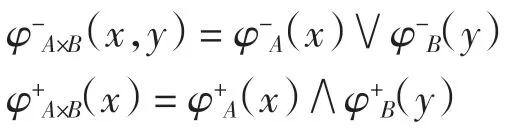
非空集合X 上的模糊集為映射μ：X→[0，1].X 的區間值模糊集為 A：X→D[0，1]，其中 D[0，1]是區間[0，1]的子區間構成的集合，如果子區間退化為一個點，則區間值模糊集就是通常的模糊集.X 的雙極值模糊集為A：X→[-1，0]×[0，1].可見，區間值模糊集和雙極值模糊集都是模糊集的推廣.

定義 4[4]設 A=[φ-A，φ+A]是半群 S 上的雙極值模糊集，如果對任意的 x、y、z∈S，有

則稱 A=[φ-A，φ+A]為半群 S 的雙極值模糊雙理想.

2 半群的（λ，μ）-雙極值模糊雙理想

定義 5設 A =[φ-A，φ+A]是半群 S 的雙極值模糊集，如果對任意 x、y、z∈S 和 0≤λ ＜ μ≤1，有

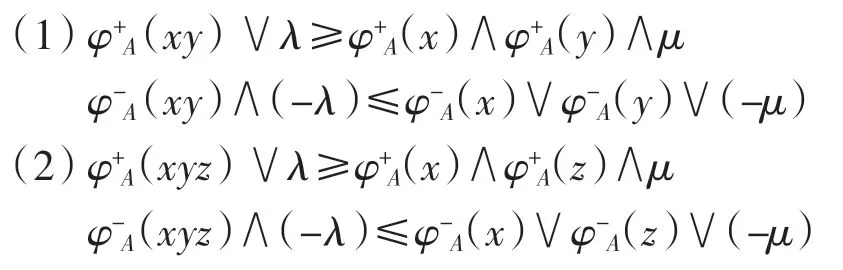
則稱 A=[φ-A，φ+A]為半群 S 的（λ，μ）-雙極值模糊雙理想.

定義 6設 A =[φ-A，φ+A]是半群 S 的雙極值模糊集，如果對任意 x、y、z∈S 和 0≤λ ＜ μ≤1，有

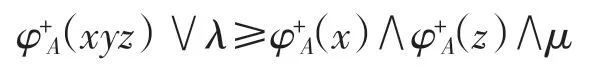
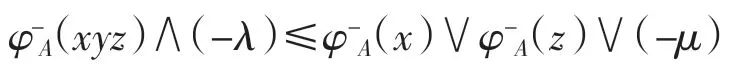
則稱 A=[φ-A，φ+A]為半群 S 的（λ，μ）-雙極值模糊廣義雙理想.

由定義 5 和定義 6 可知，半群的（λ，μ）-雙極值模糊廣義雙理想一定是（λ，μ）-雙極值模糊雙理想.

以下總假定0≤λ ＜μ≤1.

例設 S={a，b，c}，定義 S 的二元運算“·”如下

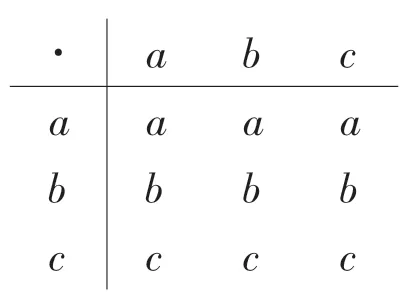
則（S，·）是半群.定義 S 的雙極值模糊集 A 為

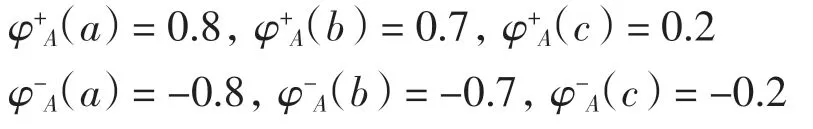
則 A=[φ-A，φ+A]為 S 上的（0.2，0.8）-雙極值模糊雙理想.定義S 的雙極值模糊集B 為

則 B=[φ-B，φ+B]為 S 上的（0.2，0.9）-雙極值模糊雙理想，但 B=[φ-B，φ+B]不是 S 上的雙極值模糊雙理想.

定理1半群的雙極值模糊雙理想一定是（λ，μ）-雙極值模糊雙理想.

證明設 A=[φ-A，φ+A]是半群 S 上的雙極值模糊雙理想，則對 x、y、z∈S，有

從而有

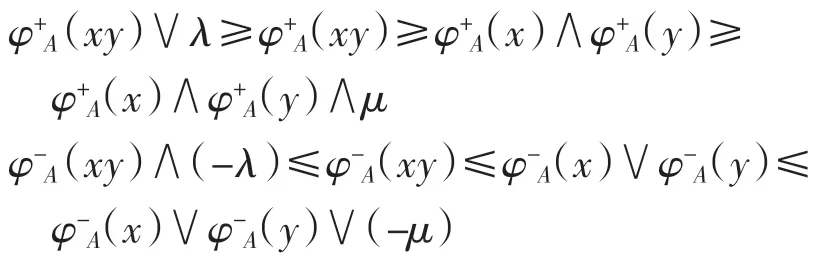
類似可得

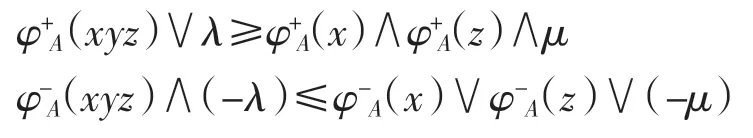
因此 A=[φ-A，φ+A]是半群 S 上的（λ，μ）-雙極值模糊雙理想.

定義 5 中若取 λ =0，μ =1，則半群的（λ，μ）-雙極值模糊雙理想就是雙極值模糊雙理想. 定理1 也表明，半群的（λ，μ）-雙極值模糊雙理想是雙極值模糊雙理想的推廣.

定理2設X 是半群S 的雙理想，則存在半群S上的（λ，μ）-雙極值模糊雙理想 A，使得 A 的（α，β）水平截集 C（A，（α，β））=X.

證明設X 是半群S 的雙理想，對于任意的（α，β）∈[-1，0]× [0，1]，定義 S 上的雙極值模糊集 A 滿足：若x∈X，則φ+A=β，φ-A=α；若x?X，則φ+A（x）=0，φ-A（x）= 0. 因此有 N（A，α）= X，P（A，β）= X，即C（A，（α，β））=X.

先證明A 滿足定義5 的（1），分2 種情況.

（1）若 x、y∈X，則 xy∈X，則有

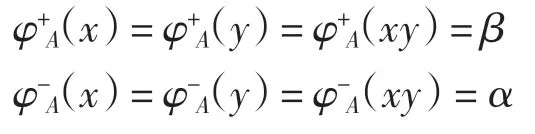
因此有

（2）若x?X 或者y?X，則φ+A（x）=0，φ-A（x）=0或φ+A（y）=0，φ-A（y）=0，則有

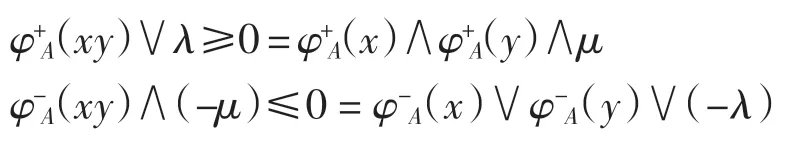
因此對任意的x、y∈S，有

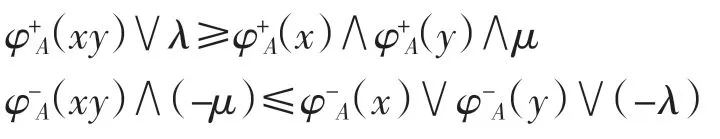
再證明A 滿足定義5 的（2），分2 種情況.

（1）若 x、y、z∈X，則 xyz∈X，則有

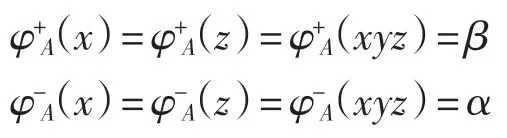
因此有

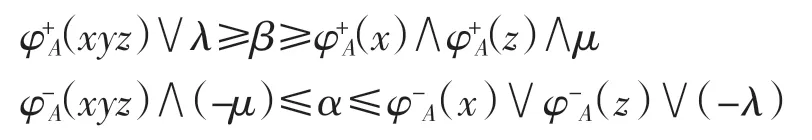
（2）若x?X 或者z?X，則φ+A（x）=0，φ-A（x）=0或φ+A（z）=0，φ-A（z）=0，則有

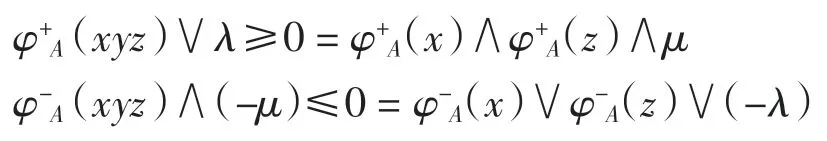
因此對任意的 x、y、z∈S，有

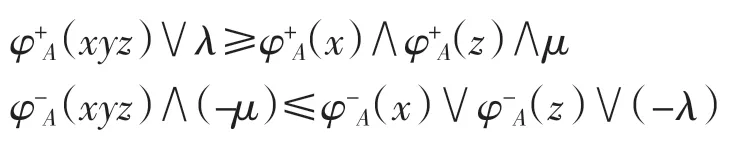
綜上，A 是半群 S 上的（λ，μ）-雙極值模糊雙理想.

推論1設X 是半群S 的廣義雙理想，則存在半群 S 上的（λ，μ）-雙極值模糊廣義雙理想 A，使得 A 的（α，β）水平截集 C（A，（α，β））=X.

定理3設A 是半群S 的雙極值模糊集，則A 是半群S 的（λ，μ）-雙極值模糊雙理想，當且僅當對任意的（α，β）∈[-1，0]× [0，1]，λ≤β≤μ，-μ≤α≤-λ，非空集 C（A，（α，β））=X 是半群 S 的雙理想.

證明（必要性）對任意的 x、y∈C（A，（α，β））=N（A，α）∩P（A，β），有φ-A（x）≤α，φ-A（y）≤α，φ+A（x）≥β，φ+A（y）≥β.由于A 是半群S 的（λ，μ）-雙極值模糊雙理想，因此有

故有 φ+A（xy）≥β，φ-A（xy）≤α. 因此 xy∈P（A，β），xy∈N（A，α）.故 xy∈C（A，（α，β）），從而 C（A，（α，β））是 S的子半群.

對任意的x、z∈C（A，（α，β）），有φ-A（x）≤α，φ-A（z）≤α，φ+A（x）≥β，φ+A（z）≥β.由于A 是半群S 的（λ，μ）-雙極值模糊雙理想，因此有

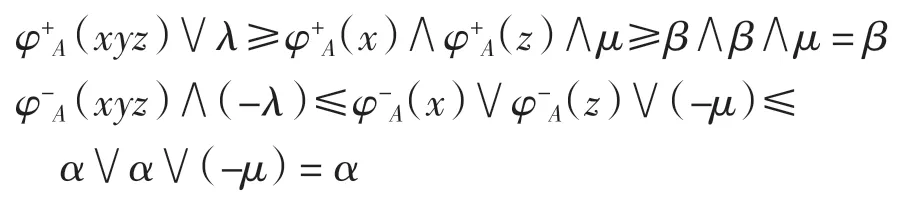
故有φ+A（xyz）≥β，φ-A（xyz）≤α.因此xyz∈C（A，（α，β）），從而 C（A，（α，β））是 S 的廣義雙理想.

綜上可知 C（A，（α，β））是半群 S 的雙理想.

（充分性）設非空集 C（A，（α，β））是半群 S 的雙理想.假設存在 a、b∈S 滿足

取（α，β）∈[-1，0]× [0，1]，滿足 λ≤β≤μ，-μ≤α≤-λ，以及

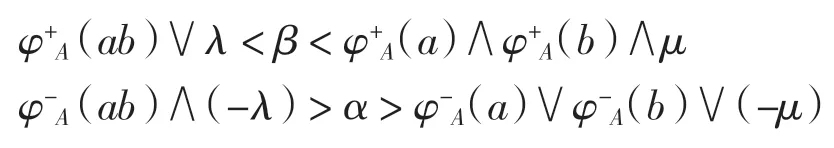
則有φ+A（a）＞β，φ+A（b）＞β，并且φ-A（a）＜α，φ-A（b）≤α.因而 a、b∈P（A，β），a、b∈N（A，α），但是 ab?P（A，β）且 ab?N（A，α）.由于 C（A，（α，β））是半群 S 的雙理想，所以 a、b∈C（A，（α，β）），這與 ab?C（A，（α，β））矛盾.故假設不成立，即對任意的x、y∈S，有

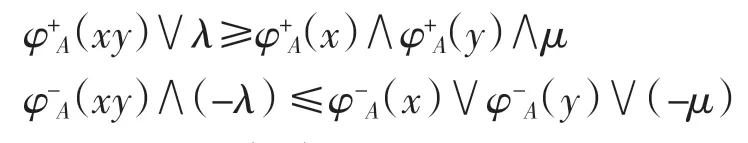
類似可以證明對任意的 x、y、z∈S，有

綜上可知A 是半群S 的（λ，μ）-雙極值模糊雙理想.

推論2設A 是半群S 的雙極值模糊集，則A 是半群S 的（λ，μ）-雙極值模糊廣義雙理想，當且僅當對任意的（α，β）∈[-1，0]× [0，1]，λ≤β≤μ，-μ≤α≤-λ，非空集 C（A，（α，β））是半群 S 的廣義雙理想.

定理4設A 是半群S 的雙極值模糊集，則A 是半群 S 的（λ，μ）-雙極值模糊雙理想，當且僅當模糊集φ+A和-φ-A都是半群 S 的（λ，μ）-模糊雙理想.

證明（必要性）若 A 是半群 S 的（λ，μ）-雙極值模糊雙理想，由定義 5 易知 φ+A是半群 S 的（λ，μ）-模糊雙理想.對任意的 x、y、z∈S，有

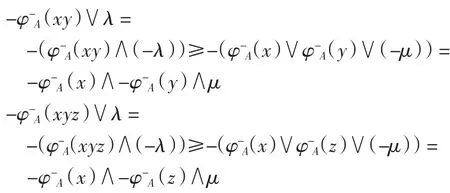
因此-φ-A是半群 S 的（λ，μ）-模糊雙理想.

（充分性）設模糊集 φ+A和-φ-A都是半群 S 的（λ，μ）-模糊雙理想，則對任意的 x、y、z∈S，有

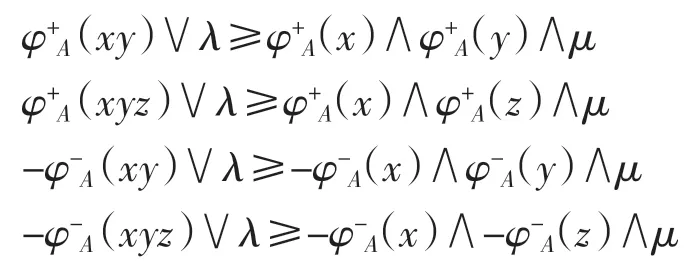
因此有

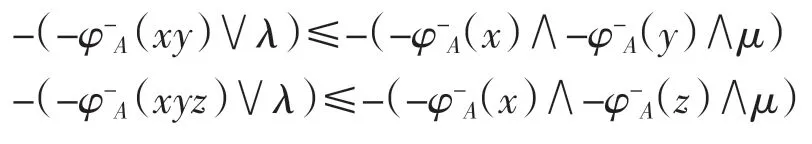
即

由定義 5 知 A 是半群 S 的（λ，μ）-雙極值模糊雙理想.

設 A=[φ-A，φ+A]和 B=[φ-B，φ+B]是非空集 X 的雙極值模糊集，則 A∩B = [φ-A∩B，φ+A∩B]也是 X 的雙極值模糊集，稱 A∩B 為 A 和 B 的交，其中：φ-A∩B（x）=φ-A（x）∨φ-B（x），φ+A∩B（x）=φ+A（x）∧φ+B（x），x∈X.

定理 5若 A 和 B 都是半群 S 的（λ，μ）-雙極值模糊雙理想，則 A∩B 也是半群 S 的（λ，μ）-雙極值模糊雙理想.

證明設 A 和 B 都是半群 S 的（λ，μ）-雙極值模糊雙理想，則對于任意的 x、y、z∈S，有

因此有

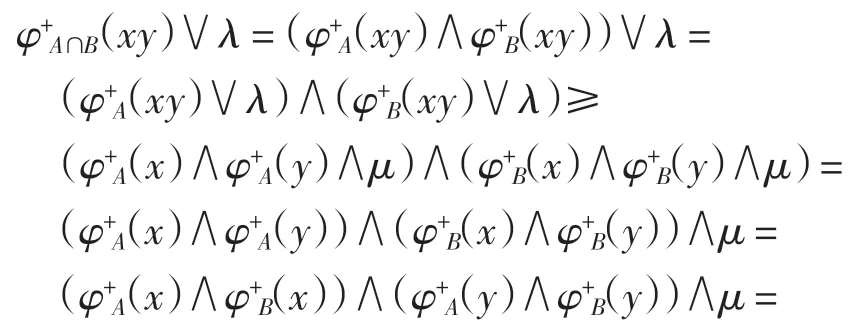
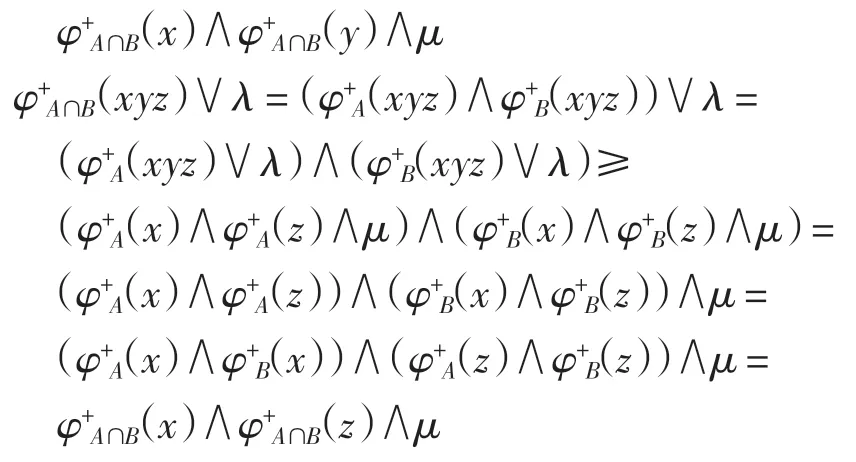
同理可得

因此 A∩B 是半群 S 的（λ，μ）-雙極值模糊雙理想.

推論 3若 A 和 B 都是半群 S 的（λ，μ）-雙極值模糊廣義雙理想，則 A∩B 也是半群 S 的（λ，μ）-雙極值模糊廣義雙理想.

推論 4若 A 和 B 都是半群 S 的（λ，μ）-雙極值模糊雙理想，則 φ+A∩B和-φ-A∩B都是半群 S 的（λ，μ）-模糊雙理想.

下面討論半群的（λ，μ）-雙極值模糊雙理想的直積的性質.設S 和R 是2 個半群，定義S×R 上的二元運算

（x1，x2）（y1，y2）=（x1y1，x2y2）（x1，x2）、（y1，y2）∈S × R則 S × R 也是半群.設 A 和 B 分別是 S 和 R 上的雙極值模糊集，定義S×R 上的雙極值模糊集A×B 為

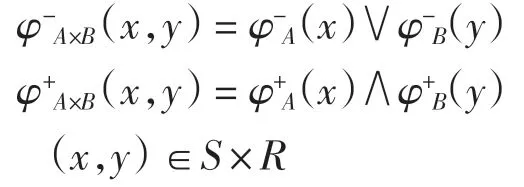
定理 6設 A 和 B 分別是半群 S 和 R 上的（λ，μ）-雙極值模糊雙理想，則 A×B 是半群 S×R 的（λ，μ）-雙極值模糊雙理想.

證明對任意的（x1，y1）、（x2，y2）、（x3，y3）∈S × R，有 A × B（（x1，y1）（x2，y2））=A × B（x1x2，y1y2）.由于 A和 B分別是半群S 和R 上的（λ，μ）-雙極值模糊雙理想，因此有

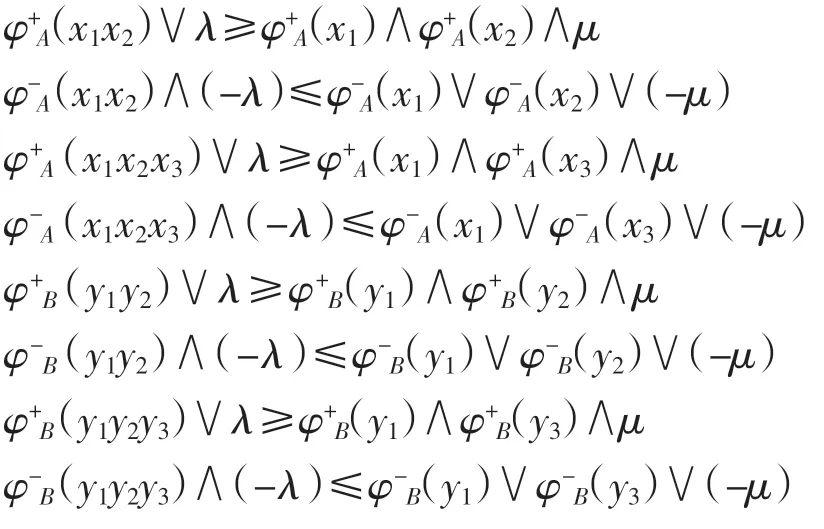
故有

類似可得

因此 A × B 是半群 S× R 的（λ，μ）-雙極值模糊雙理想.

推論 5設 A 和 B 分別是半群 S 和 R 上的（λ，μ）-雙極值模糊廣義雙理想，則 A × B 是半群 S × R 的（λ，μ）-雙極值模糊廣義雙理想.

推論 6設 A 和 B 分別是半群 S 和 R 上的（λ，μ）-雙極值模糊雙理想，則 φ+A×B和-φ-A×B都是半群 S × R的（λ，μ）-模糊雙理想.