壓強對MgO 光彈系數(shù)影響的第一性原理研究

張佳佳，趙 輝

（天津師范大學(xué)物理與材料科學(xué)學(xué)院，天津300387）

在壓強作用下，光學(xué)各向同性介質(zhì)發(fā)生彈性形變，導(dǎo)致折射率發(fā)生改變，這種現(xiàn)象稱為光彈效應(yīng)[1].描述光彈效應(yīng)的光彈系數(shù)有2 種，一種反映介質(zhì)折射率變化量對壓強的響應(yīng)程度，用壓光系數(shù)Π 表示，另一種反映折射率變化量對彈性形變的響應(yīng)程度，用彈光系數(shù)Q 表示[2].光彈效應(yīng)最早于1815 年，由布儒斯特[3-4]在膠狀物中發(fā)現(xiàn)，1816 年，布儒斯特又在玻璃和立方晶體等透明固體中證明光彈效應(yīng)的存在.這一現(xiàn)象的發(fā)現(xiàn)很快引起關(guān)注，大量晶體和非晶體的光彈效應(yīng)陸續(xù)被觀測研究，關(guān)于光彈效應(yīng)的數(shù)學(xué)模型與本質(zhì)規(guī)律探究也在20 世紀這100 年中取得大量成果[5].

在光彈效應(yīng)相關(guān)研究中，作為最常見的巖鹽晶體，由于MgO 的光彈系數(shù)與大多數(shù)巖鹽晶體符號相反，因此引起大量關(guān)注[5-8].MgO 的壓光系數(shù)與彈光系數(shù)先后通過不同實驗方法測得，但與實驗所得光彈系數(shù)存在明顯差異[2，7，9].2013 年，研究人員通過第一性原理模擬證明，彈光系數(shù)不同分量之間的差異由光彈效應(yīng)色散引起[10].2017 年，研究人員對多種混合氧化物永久致密玻璃的光彈實驗表明，混合氧化物的壓光系數(shù)隨壓強增大而減小[11]，這表明壓強可能成為繼入射光頻率和環(huán)境溫度等因素后，另一個值得探究的影響介質(zhì)光彈系數(shù)的因素. 目前關(guān)于壓強對壓光光彈系數(shù)影響的研究較少，因此本研究基于第一性原理計算了MgO 壓光系數(shù)和彈光系數(shù)，進一步分析了MgO光彈系數(shù)與壓強的關(guān)系，得到不同壓強下彈光系數(shù)的變化規(guī)律，從而對光彈效應(yīng)的實驗研究和應(yīng)用提供理論支持.

1 計算方法與原理

1.1 光彈效應(yīng)理論

光彈系數(shù)由Pockels 光彈效應(yīng)理論[12]得到，該理論建立在2 個基本假設(shè)基礎(chǔ)上：

（1）球的光學(xué)參數(shù)；

（2）當應(yīng)變在彈性限度內(nèi)時，形變引起的變化量可以表示為9 個壓強分量pij或9 個應(yīng)變分量ηij（i，j=x，y，z）的齊次線性函數(shù).

下面以笛卡爾坐標系下理想晶體為例，未施加壓強時，晶體的折射率橢球為[1]

式（1）中：εij為晶體的介電張量分量.

設(shè)ηij為晶體的折射率分量，在可見光頻率范圍內(nèi)有[13]

對晶體施加壓強pkl（k，l=x，y，z）后，晶體發(fā)生彈性形變，根據(jù)式（1）的假設(shè)，形變只改變折射率系數(shù)，則形變后折射率橢球變?yōu)?/p>

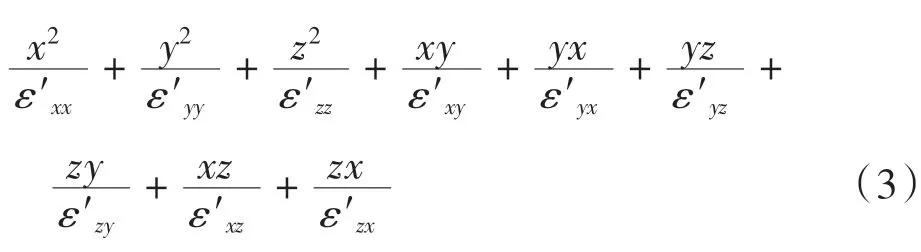
根據(jù)式（2）的假設(shè)，形變前后系數(shù)變化與壓強存在線性關(guān)系

或與應(yīng)變存在線性關(guān)系

式（4）和式（5）中：πijkl和 qijkl分別為壓光系數(shù) Π 和彈光系數(shù)Q 的分量.式（2）的假設(shè)認為，晶體應(yīng)變與所受壓強為線性關(guān)系，因此式（4）與式（5）是等價的.一般認為正的壓強表示壓縮，會引起負的應(yīng)變，因此，式（4）和式（5）存在正負號的差別.

壓光系數(shù)Π 和彈光系數(shù)Q 中獨立分量的個數(shù)與晶體對稱性直接相關(guān)[14].由于介電張量ε 中εij=εji，壓強張量P 中pij=pji，原先具有81 個分量的壓光系數(shù)和光彈系數(shù)的獨立分量減少為36 個[5，12]，為了表述方便，各分量表示簡化如下：ε1= εxx，ε2= εyy，ε3= εzz，ε4=εzy，ε5= εxz；ε6= εyx，p1=pxx，p2=pyy，p3=pzz，p4=pzy，p5=pxz，p6=pyx.

則式（4）和式（5）變?yōu)?/p>

式（6）和式（7）中：i、j=1、2、3、4、5、6.由式（2）可得，在可見光頻率范圍內(nèi)有

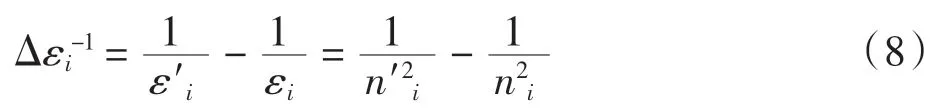
當施加壓強較小時，加壓后的折射率ni′與加壓前的折射率ni近似相等，因此

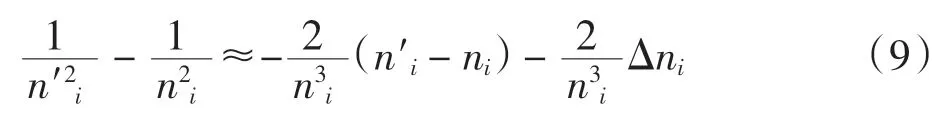
結(jié)合式（6）～式（9）分別求得壓光系數(shù)πij和彈光系數(shù)qij

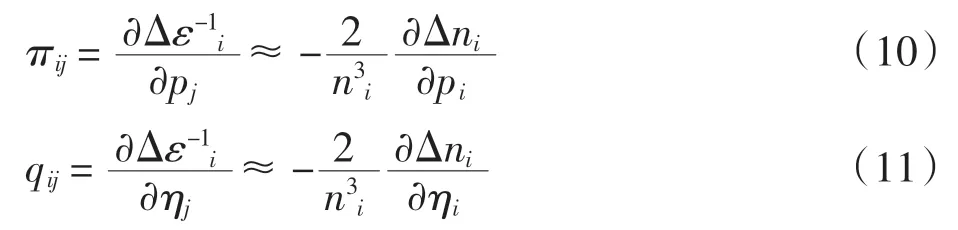
1.2 MgO 光彈系數(shù)計算

MgO 晶體具有面心立方結(jié)構(gòu)，根據(jù)晶體對稱性，MgO 的壓光系數(shù)和彈光系數(shù)中獨立分量只有2 個[1，5]，分別為

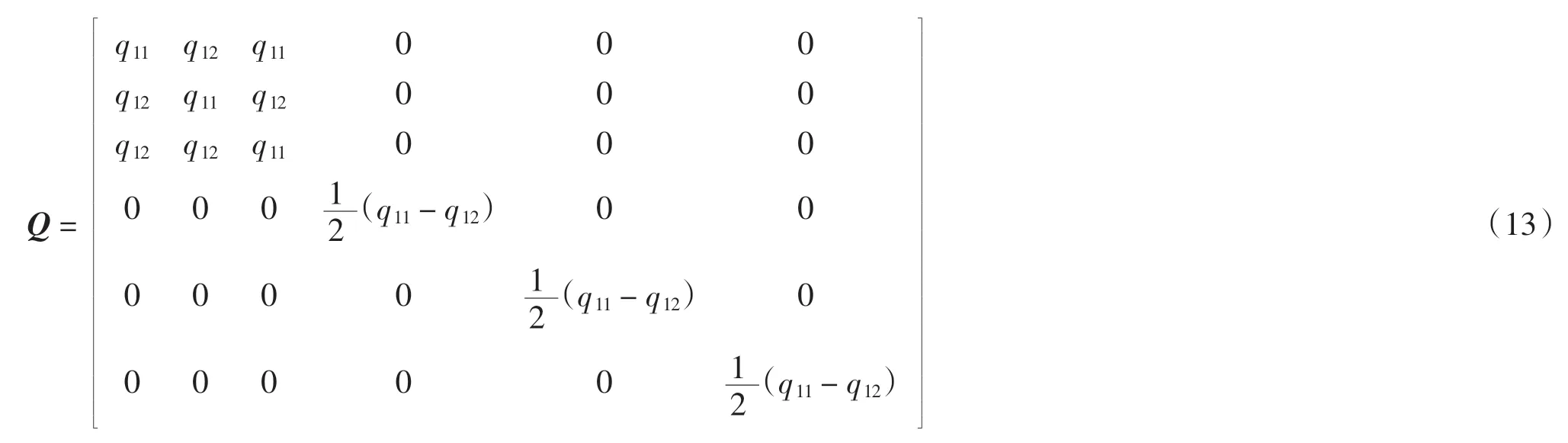
以壓光系數(shù)為例，對MgO 晶體施加均勻壓強，即靜水壓ph（hydrostatic pressure），p1=p2=p3=ph（其他分量為 0）.加壓前后介電常數(shù) ε1= ε2= ε3=ε，ε′1=ε′2=ε′3= ε（其他分量為 0）.根據(jù)式（6）有

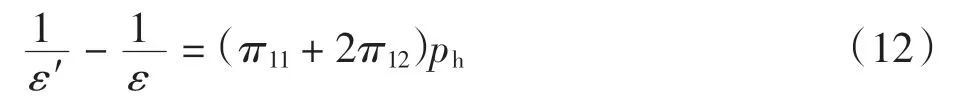
根據(jù)式（10）進一步有

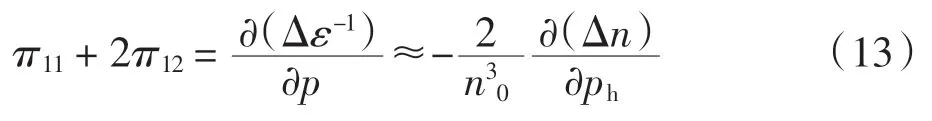
式（13）中：n0為加壓前 MgO 的折射率.根據(jù)式（13）對MgO 施加均勻壓強，并測量折射率的變化量，得到壓光系數(shù) π11+2π12的值.

對MgO 施加某一晶體主軸方向的壓強（如z 軸），即單軸加壓pu（uniaxial pressure）.此時，p3=pu（其他壓強分量為0），MgO 由立方結(jié)構(gòu)變?yōu)樗姆浇Y(jié)構(gòu)，x 與y軸方向等價，與z 方向不等價，根據(jù)晶體的對稱性，加壓前 MgO 的介電常數(shù) ε1=ε2=ε3=ε；加壓后，ε′1=ε′2≠ε′3= ε.根據(jù)式（7）有

式（14）與式（15）相減得

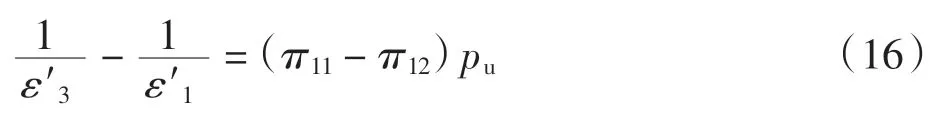
根據(jù)式（10）進一步有

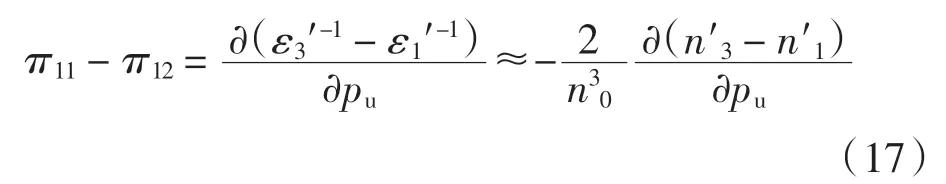
式（17）中：n 為未施加壓強時 MgO 的折射率，n′3和 n′1分別為施加壓強后平行于壓強和垂直于壓強方向的折射率.由式（17）可知，對MgO 施加平行于z 主軸的壓強，并測量加壓后平行和垂直于壓強方向的折射率的差值，即可求得壓光系數(shù)π11-π12.

根據(jù)同樣的方法，得到彈光系數(shù)分量為

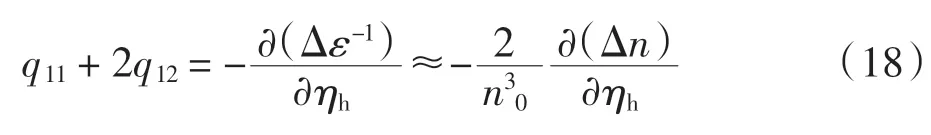
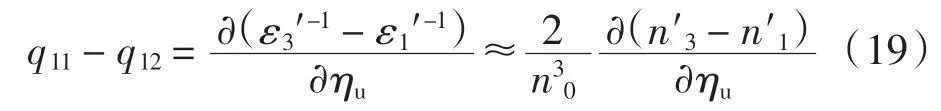
式（18）中：ηh為施加均勻壓力 ph后 MgO 的形變，此時，每個主軸方向的應(yīng)變是相同的，均為ηh.式（19）中ηu為沿z 軸方向施加單軸壓力pu后，MgO 晶體的應(yīng)變，此時，應(yīng)變主要沿z 軸方向，記為ηu.由式（13）和式（17）即可得MgO 晶體壓光系數(shù)中2 個獨立分量π11和 π12的值.同理，由式（18）和式（19）可得彈光系數(shù)中2 個獨立分量 q11和 q12的值.

1.3 模擬計算參數(shù)設(shè)置

MgO 光彈系數(shù)計算使用基于第一性原理的CASTEP（cambridge serial total energy package）軟件包[15]. 交換關(guān)聯(lián)勢采用局域密度近似（LDA）中的CA-PZ 方法[16-17].贗勢選擇規(guī)范保守勢[18]，氧原子的價電子為2s22p4，鎂原子價電子為2s22p63s2. 布里淵區(qū)積分k 點取樣使用Monkhorst-pack 方法[19]，未施加壓強與施加均勻壓強時k 點網(wǎng)格為4×4×4，施加主軸z 方向壓強時，k 點網(wǎng)格為5×5×3.截止能選取為990 eV，使自洽場精度達到5×10-7eV/atom，后續(xù)加壓計算中均選取此截止能.

2 結(jié)果與討論

2.1 壓光系數(shù)

對 MgO 施加 0 ～ 0.7 GPa 的均勻壓強，MgO 的折射率逐漸降低.本研究利用CASTEP 計算不同壓強下MgO 的折射率n（p）和未加壓時MgO 的折射率n0（n0=1.791 1），得到兩者的差值

圖1 為折射率變化量Δn 與壓強P 的變化關(guān)系.Vedam 和 Schmidt[7]對 MgO 施加 0～0.7 GPa 的均勻壓強，并利用干涉法得到折射率隨壓強的變化曲線.圖1中 Bogardus 和 Bridgman 兩條曲線分別由 Vedam 和Schmidt[7]利用 Bogardus[20]的彈光系數(shù)和 Bridgman[21]的三階彈性系數(shù)得到.

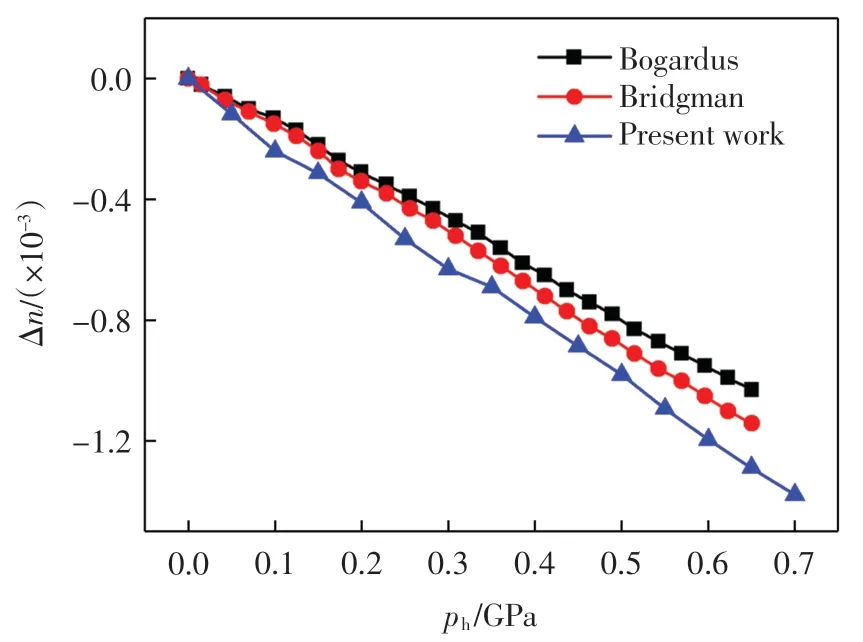
圖1 不同均勻壓強ph 下折射率變化量Δn 的變化趨勢Fig.1 Changes of refractive index Δn under different hydrostatic pressure ph

由圖1 可以看出，折射率變化量Δn 隨壓強ph的增大而減小.由第一性原理計算得到的曲線斜率近似為-1.89×10-3，與 Bogardus 曲線（斜率為-1.63 ×10-3）的誤差為 16.0%，與 Bridgman 曲線（斜率為-1.82×10-3）的誤差為3.8%.

根據(jù)式（13）與圖1 中3 條曲線得到壓光系數(shù)π11+2π12如圖 2 所示.

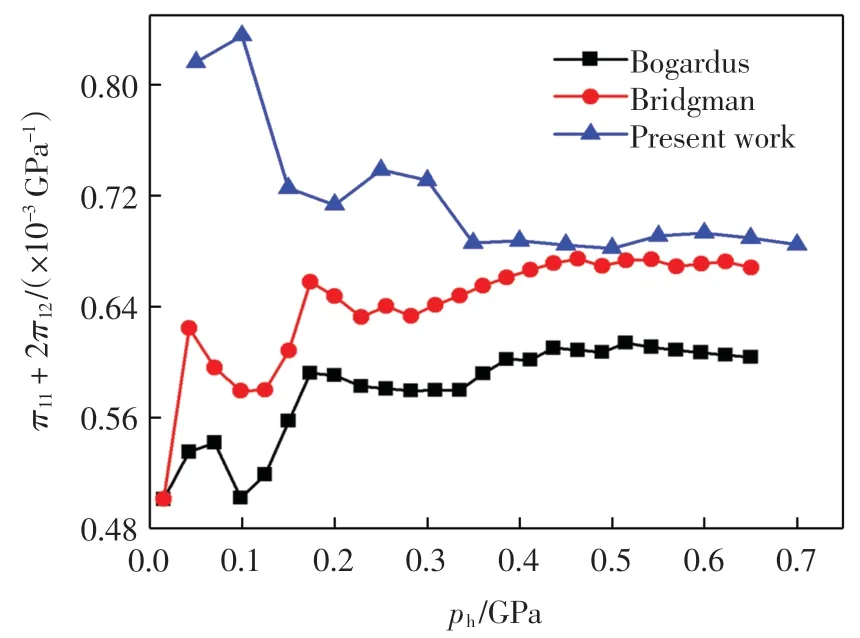
圖2 不同均勻壓強ph 下π11+2π12 的變化趨勢Fig.2 Changes of π11+2π12 under different hydrostatic pressure ph

由圖2 中3 條曲線可以看出，壓強小于0.4 GPa時，π11+2π12的波動較大，這可能是由于應(yīng)變太小，導(dǎo)致測量誤差較大[7].壓強大于0.4 GPa 時，3 條曲線均趨于穩(wěn)定值，此時，CASTEP 計算所得 π11+2π12=5.6×10-4GPa-1，Bogardus 曲線趨于 6.1 × 10-4GPa-1，Bridgman 曲線趨于6.7×10-4GPa-1.CASTEP 計算結(jié)果與兩者誤差分別為8.2% 和16.4%.由于CASTEP 模擬的為理想晶體，因此會與實驗結(jié)果產(chǎn)生誤差.此外，由于實驗參數(shù)選取不同，2 個實驗本身也存在較大誤差[7].

對MgO 施加z 軸方向的壓強，根據(jù)式（17）得到壓光系數(shù)π11－π12與壓強的關(guān)系如圖3 所示.施加z 軸方向壓強后，MgO 變?yōu)樗姆骄w，產(chǎn)生雙折射[1]，壓光系數(shù)π11－ π12可以通過這一現(xiàn)象測量得到[7]. Giardini等[2]利用這一原理測得對MgO 施加0.056 GPa 壓強時，π11－ π12=1.25× 10-3GPa-1，這與本研究所得結(jié)果 π11－π12=1.22×10-3GPa-1接近，說明第一性原理模擬計算光彈系數(shù)具有較高的可信度.由圖3 可以看出，壓強小于0.35 GPa 時，壓光系數(shù)π11－π12隨壓力的增加迅速減小，因此，由于對MgO 施加壓強不同，不同實驗的測量結(jié)果必然存在差距.

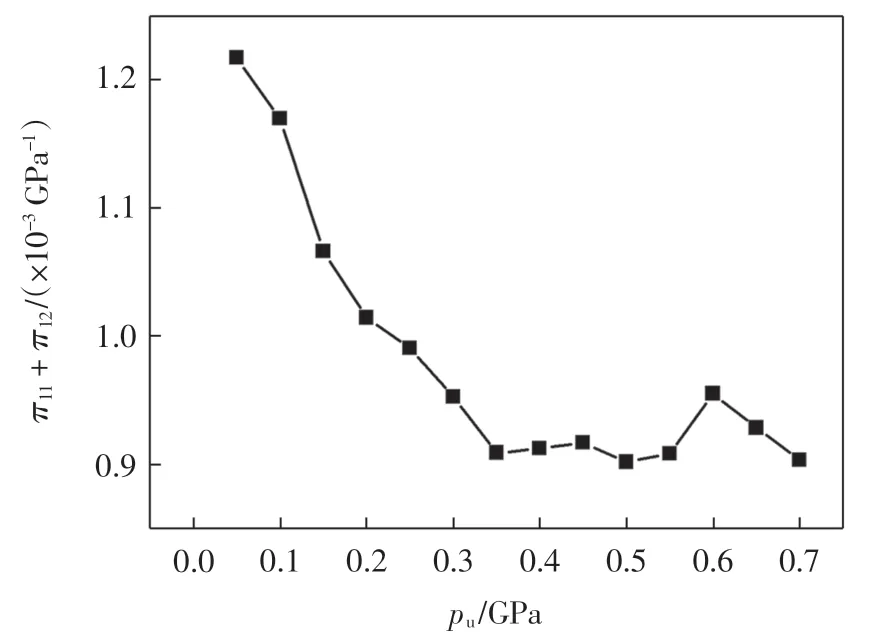
圖3 不同單軸壓強pu 下π11－π12 的變化趨勢Fig.3 Changes of π11－ π12 under different uniaxial pressure pu

根據(jù)圖2 和圖3 計算結(jié)果得到壓光系數(shù)π11和π12的值如圖4 所示.

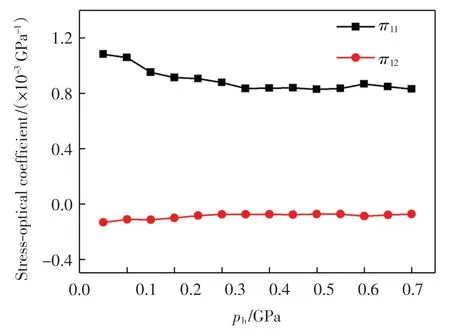
圖4 不同壓強ph 下壓光系數(shù)的變化趨勢Fig.4 Changes of stress-optical coefficients under different pressure ph

由圖4 可以看出，壓強對π12值的影響較小，但對π11值的影響較大，特別是壓強小于 0.2 GPa 時，π11隨壓強增大呈現(xiàn)明顯下降趨勢.

2.2 彈光系數(shù)

圖 5 為對 MgO 施加均勻壓強 0～0.7 GPa 時，MgO應(yīng)變隨壓強的變化情況.本研究和Bogardus 曲線均采用非線性彈性理論[22]，曲線Bridgman 采用Bridgman 提出的經(jīng)驗參數(shù)，得到MgO 在不同壓強下的應(yīng)變.

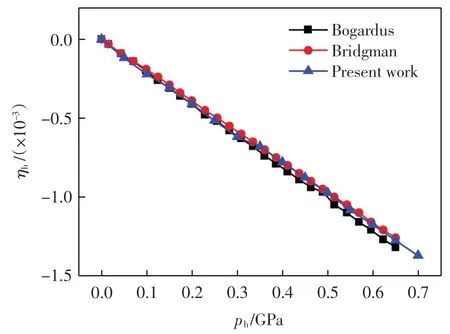
圖5 不同均勻壓強ph 下應(yīng)變ηh 變化趨勢Fig.5 Changes of strain ηh under different hydrostatic pressure ph

由圖5 可以看出，3 條曲線基本一致，說明第一性原理計算應(yīng)變可信度較高.同時，3 條曲線均由非線性理論得到，但應(yīng)變隨壓強近似為線性變化，這是由于MgO 彈性系數(shù)較大，施加壓強較小，應(yīng)變較小所導(dǎo)致的.

結(jié)合圖1 折射率變化量與壓強關(guān)系以及圖5 應(yīng)變與壓強關(guān)系，得到折射率變化量隨應(yīng)變變化曲線如圖6 所示.

圖6 折射率變化量Δn 與應(yīng)變ηh 變化關(guān)系Fig.6 Changes of refractive index Δn with strain ηh

由圖6 可知，折射率變化量與應(yīng)變近似為線性關(guān)系.由第一性原理計算得到的曲線斜率近似為1.01，與Bogardus 曲線（斜率為 0.80）的誤差為 26.2%，與Bridgman 曲線（斜率為0.93）的誤差為8.6%.

根據(jù)式（18）及圖6 得到彈光系數(shù)q11+2q12如圖7所示.由圖7 中3 條曲線可知，壓強小于0.4 GPa 時，q11+2q12隨壓強波動較大，且3 條曲線波動趨勢相近；壓強高于0.4 GPa 時，隨著壓強的增加，由第一性原理計算得到q11+2q12的值趨近于-0.351，與Bogardus 曲線中 q11+ 2q12的趨近值-0.300 的誤差為 17%，與Bridgman 曲線中q11+2q12的趨近值-0.346 的誤差為1.4%.由0～0.7 GPa 整個加壓過程可知，第一性原理計算結(jié)果相對更穩(wěn)定.

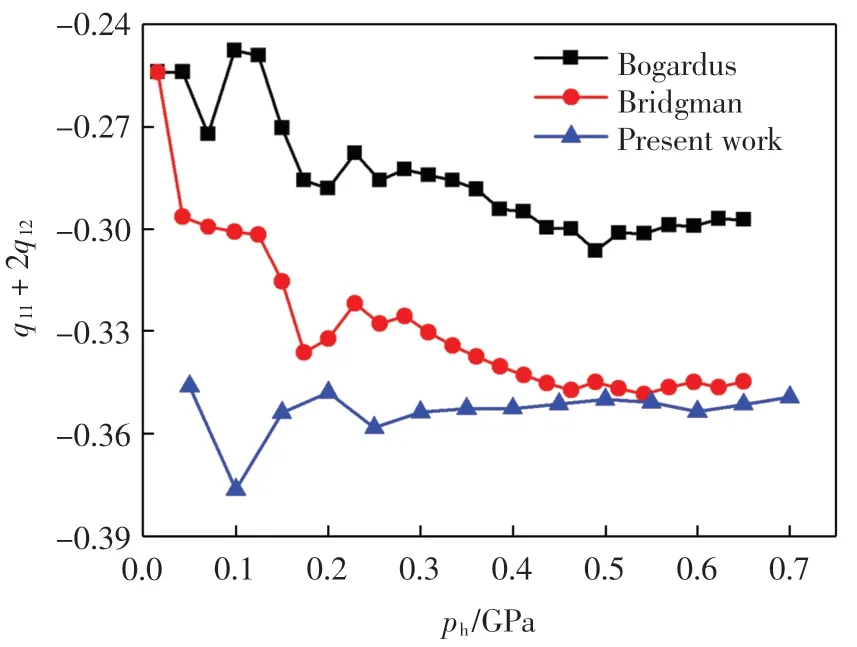
圖7 不同均勻壓強ph 下q11+2q12 的變化趨勢Fig.7 Changes of q11+2q12 under different hydrostatic pressure ph

對MgO 施加0～0.7 GPa 平行于z 軸方向的壓強，得到彈光系數(shù)q11－q12值如圖8 所示.

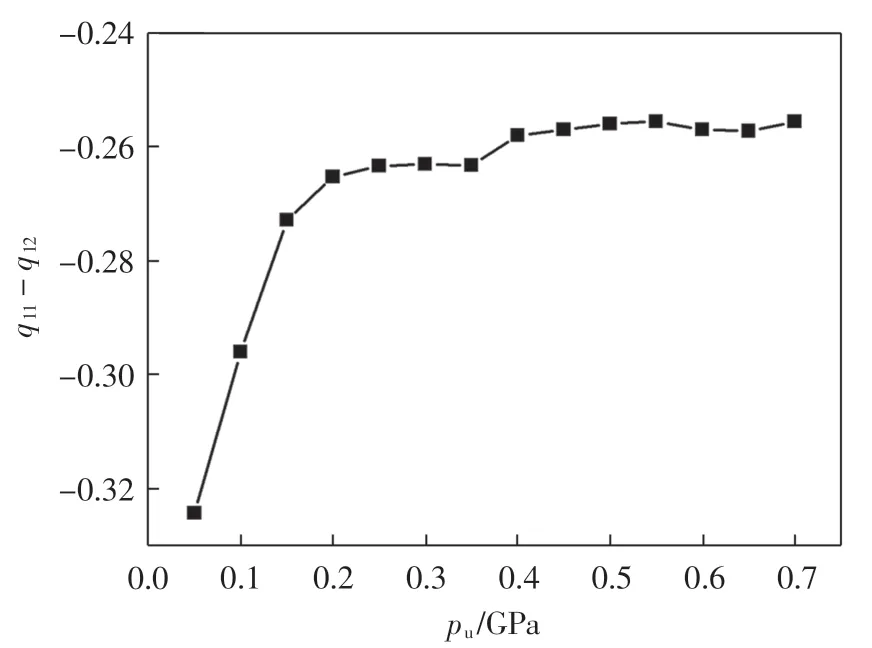
圖8 不同單軸壓強pu 下q11－q12 的變化趨勢Fig.8 Changes of q11－q12 under different uniaxial pressure pu

由圖8 可以看出，與圖4 壓光系數(shù)π11－π12相似，壓強較小（小于0.2 GPa）時，q11－q12隨壓強迅速增加.由壓強雙折射產(chǎn)生原因可知[1]，此時沿z 軸方向振動與沿x 和y 軸方向振動的入射光折射率差值迅速增大，雙折射現(xiàn)象更加顯著.由圖7 也可以預(yù)測，當壓強增大時，由于q11－q12的值趨于穩(wěn)定，雙折射值也趨于穩(wěn)定值.

根據(jù)圖7 和圖8 計算結(jié)果得到彈光系數(shù)獨立分量q11和q12的值如圖9 所示.當壓強小于0.1 GPa 時，q12隨著壓強的增加明顯減小. 當壓強小于0.15 GPa時，q11隨著壓強的增加明顯增大.整體考慮，q11和q12的值比較穩(wěn)定，分別在-0.260 與-0.025 上下浮動.與Vadem 等[7]所得 q11= -0.265 的誤差為 1.9%，與 q12=-0.017 的誤差為47.1%.這與其他實驗和理論研究所得q12的差距較大，甚至出現(xiàn)符號不一致的情況[2，10].產(chǎn)生上述差距的原因為，第一性原理計算采用的入射光頻率為光頻波段（頻率趨于無窮大），實驗則多采用可見光的某一頻率波段，本研究基于第一性原理計算所得結(jié)果符合Erba 和Dovesi 基于第一性原理計算所得MgO 光彈系數(shù)的色散規(guī)律.

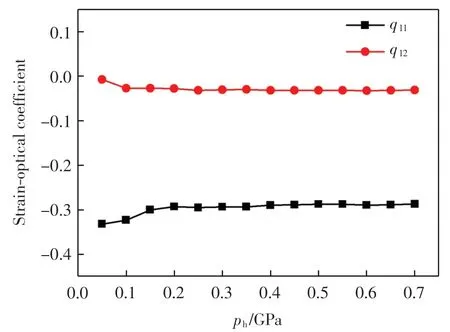
圖9 不同壓強ph 下彈光系數(shù)的變化趨勢Fig.9 Changes of strain-optical coefficients under different pressure ph

3 結(jié)論

（1）由壓光系數(shù)和彈光系數(shù)實驗和第一性原理模擬計算結(jié)果可知，壓強較小時，測定壓光系數(shù)與彈光系數(shù)均隨壓強存在較大波動.特別是可以由實驗直接測量的系數(shù) π11+ 2π12、π11- π12、q11+ 2q12和 q11- q12，這些量在壓強較小時測量結(jié)果波動明顯，這可能是由于電子極化率在壓強較小時波動更大引起的.

（2）壓光系數(shù)獨立分量π11和π12以及彈光系數(shù)獨立分量q11和q12只在小范圍壓強內(nèi)增大或減小，且變化量較小，之后保持在穩(wěn)定值不變，這可能是由于壓強增大后MgO 彈性系數(shù)增大，導(dǎo)致MgO 更難被壓縮造成的.

（3）光彈效應(yīng)和光彈系數(shù)與介質(zhì)電子結(jié)構(gòu)密切相關(guān)[23]，對微觀結(jié)構(gòu)的研究和精密光學(xué)器材的制備具有重要的指導(dǎo)意義[24].本研究補充了壓強對光彈系數(shù)的作用，對不同壓強條件下MgO 光彈效應(yīng)的變化具有積極的指導(dǎo)作用.后續(xù)研究將從MgO 電子結(jié)構(gòu)出發(fā)，以揭示壓強對MgO 電子結(jié)構(gòu)的影響，從而闡釋MgO 光彈效應(yīng)隨壓強變化的原因.