帶落角約束與過載約束的尋初比例導引法*
王煜東,許承東,鄭學恩,孫光輝,簡益梅
(北京理工大學宇航學院, 北京 100081)
0 引言
隨著現代戰爭的發展,對導彈末端精確打擊的要求越來越高。落角是導彈命中目標時速度矢量與水平面之間的夾角,落角越大,對目標的擊頂效果越好,對落角提出更高的要求,能夠使導彈末制導段的參數更加合理。國內外大多采用帶落角約束的制導律來對落角加以限制,該方法主要分三類[1]:一是采用最優制導律的方法,如馮艷清[2]等人設計了帶落角約束的三維導引律,可以對靜止目標及低速目標以一定攻擊角度進行攻擊;張友安[3]等人結合落角、目標攻角及脫靶量設計了一種二次型最優制導律,能夠滿足在高精度的前提下以一定落角進行攻擊。二是采用滑模制導律,Harl N[4]等人采用視線角整形技術推導出具有攻擊時間與攻擊角度約束的制導律,但是制導律形式十分復雜,制導指令需要大量迭代,只能離線完成;楊峰[5]等人提出了帶落角約束的模糊變結構導引律,滿足了制導精度與落角要求。三是采用改進比例導引法,Lee C H[6]等人在傳統的比例導引法上加入落角約束,提出了帶落角約束的偏置比例導引,但是該方法僅對固定目標有較好的效果,且還需要對剩余飛行時間進行估計,實用性受限。高峰[7]等人設計了一種三維聯合偏置比例導引律,采用時變比例系數可對高速目標與低速目標分別攔截,是一種普適的制導律,但是在攔截初始段的需用過載要求比較大,并且還需要精確的估計剩余時間才能滿足落角精度。比例導引法理論成熟,成果豐富,工程實現簡單,因此文中采用比例導引法,在理論上推導落角的數學表達式,建立落角預測模型,根據模型結果選取恰當的比例系數,即可實現對預計目標以一定的落角進行打擊,只需在導彈平飛段選擇合適的攻擊參數與導彈比例系數即可。
為簡化分析,文中以圖像制導導彈[8]為例,導彈最大可用過載為5,攻擊目標為敵方坦克,命中目標時落角大于30°時即可達到理想效果。
1 尋初比例導引法
比例導引法是指導彈在攻擊目標的導引過程中,導彈速度矢量旋轉的角速度與目標線旋轉角速度成比例。導彈在飛行過程中過載時刻在變化,傳統的比例導引法無法保證命中時的落角,因此提出一種改進比例導引法,該方法通過尋找滿足過載約束與落角約束的初始值,其中落角會隨著初始目標線角q0增大而增大,過載會隨著轉比距離r0增大而減小,因此需要找到合適的q0及r0,使導彈命中目標時既滿足過載約束,又能符合落角要求。
1.1 建立導彈相對運動方程
按比例導引時,導彈與目標之間的相對運動方程組為:
(1)
當導彈在鉛垂面內從某一高度平飛到開始啟動比例導引法進行末制導,導彈與目標相對運動關系如圖1所示。
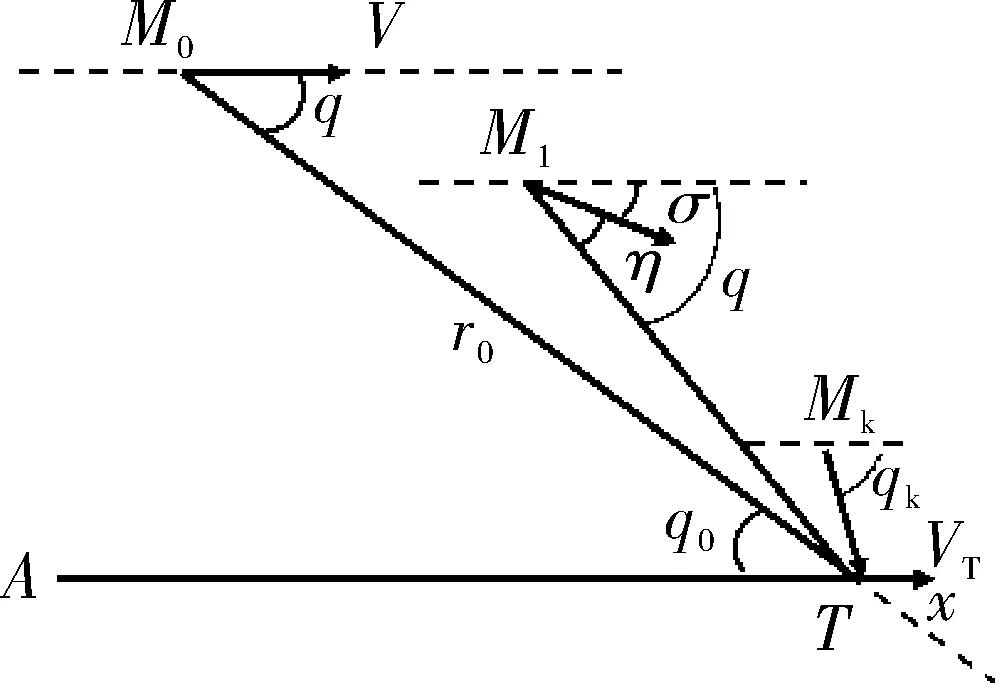
圖1 導彈與目標相對運動關系
圖中M0,M1,Mk分別是導彈由平飛段轉到比例導引的初始位置,中間某一時刻位置,及命中目標時的位置;T為目標位置;初始距離為r0;選取Ax軸作為基準線,初始目標線角為q0,命中目標時目標線角為qk,導彈速度矢量及目標速度矢量與目標線之間的夾角為前置角,分別記作η,ηT;導彈速度矢量與目標速度矢量與基準線之間的夾角為導彈彈道角及目標航向角,記σ,σT。
1.2 落角的幾何關系
落角即導彈速度矢量與水平線之間的夾角,由圖1可知,落角近似等于命中目標時目標線角qk,由于qk未知,但是由幾何關系可得:
qk=q0+(qk-q0)
(2)
將qk-q0記作目標線偏轉角△q,得到落角公式:
qk=q0+Δq
(3)
由于初始q0為已知量,求得目標線偏轉角Δq的范圍,即可得出落角qk的范圍。
1.3 Δq的解析表達
將式(1)中的第二個方程單獨分析:
(4)
考慮到命中目標時距離為0,所以當rk=0時,式(4)化簡為:
Vsinη=VTsinηT
(5)
將幾何關系ηT=qk-σTk代入上式得到:
Vsinη=VTsin(qk-σTk)
(6)
由比例導引法定義可得:
η-η0=(1-K)(qk-q0)
(7)
聯立式(6)與式(7),消去導彈速度前置角η,并將導彈速度與目標速度的速度比p引入該方程可得:
(8)
將式(8)右端qk-q0記作△q得到目標線偏轉角的解析表達式為:
(9)
由式(9)可以看出,目標線偏轉角與轉比距離r0無關。
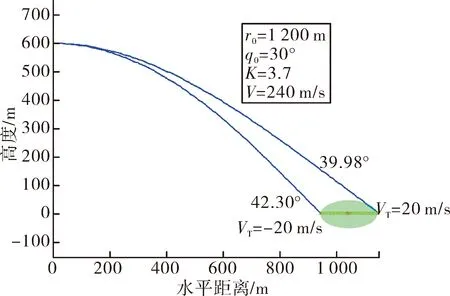
為簡化分析,飛行速度保持恒定V=240 m/s,導彈射程為1~10 km,最大法向過載為n=5,導引頭最大探測距離為3 km,導引頭瞬時視場為4°×3°[9]。將數值進行仿真,畫出彈道曲線如圖2所示。
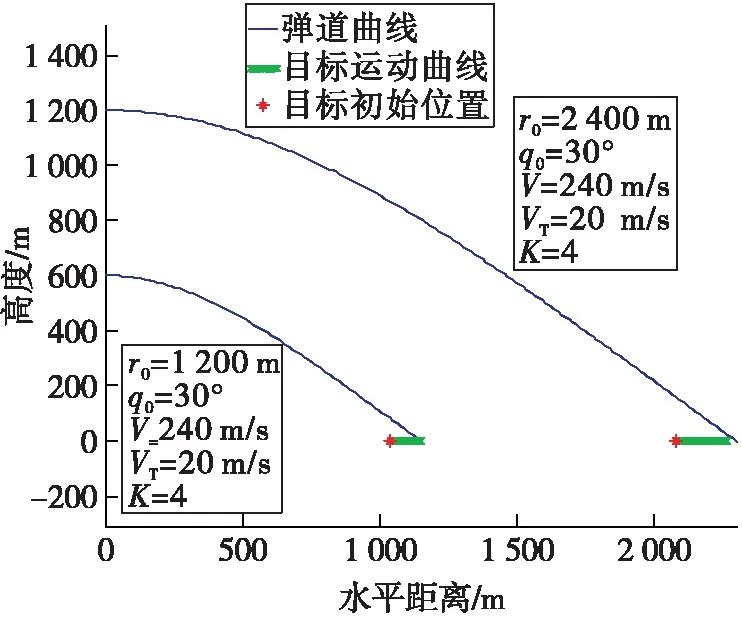
圖2 不同轉比距離的彈道曲線對比
觀察到僅改變初始距離r0,q0為30°保持不變,兩次計算出的落角均是38.99°,驗證落角與r0無關。
1.4 落角預測模型
觀察到式(9)中,式右端包含3個參數K、p、η0,及一個未知量qk,無法精確求得目標線偏轉角的大小,但是由于sinqk在實際情況中有取值范圍,即:
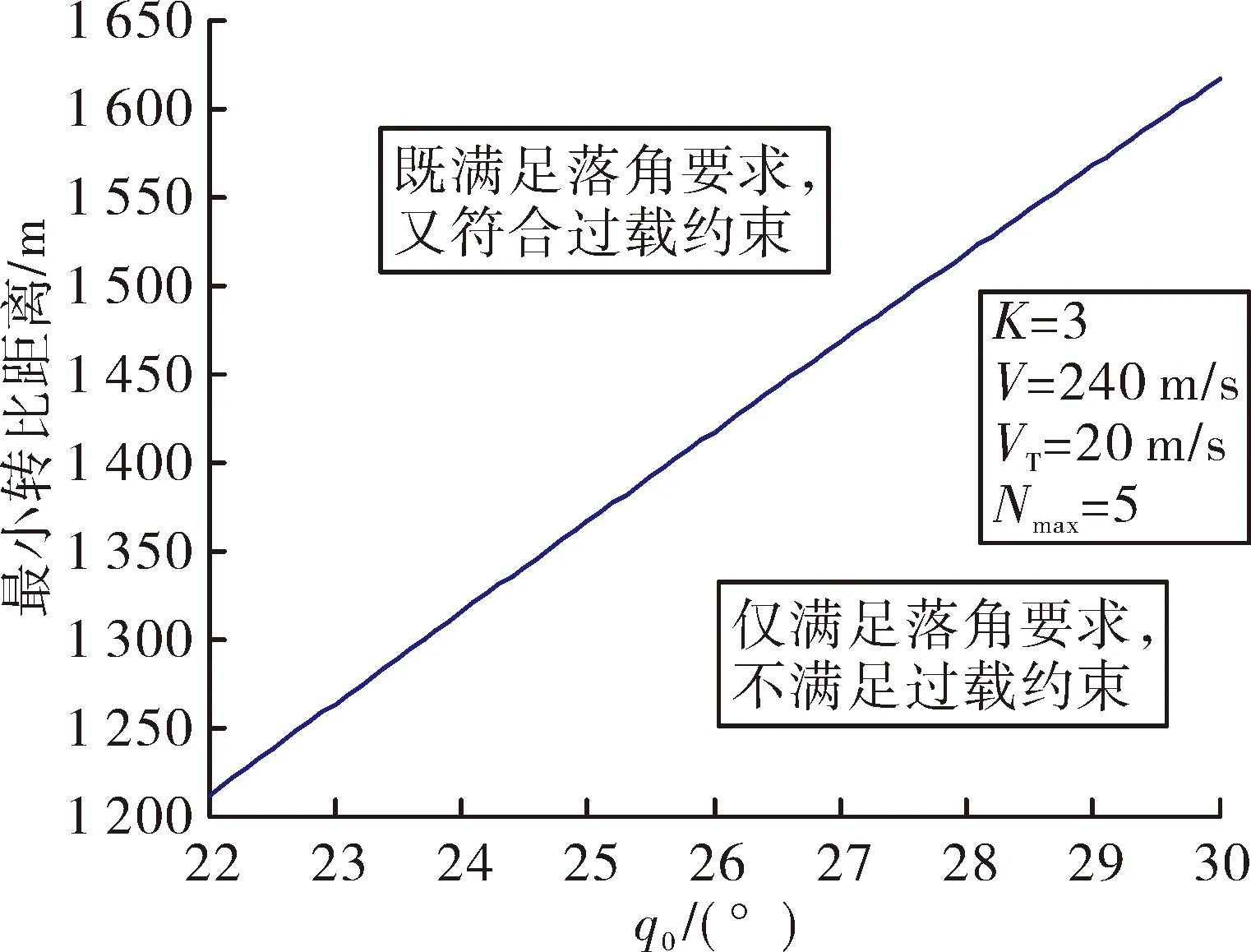
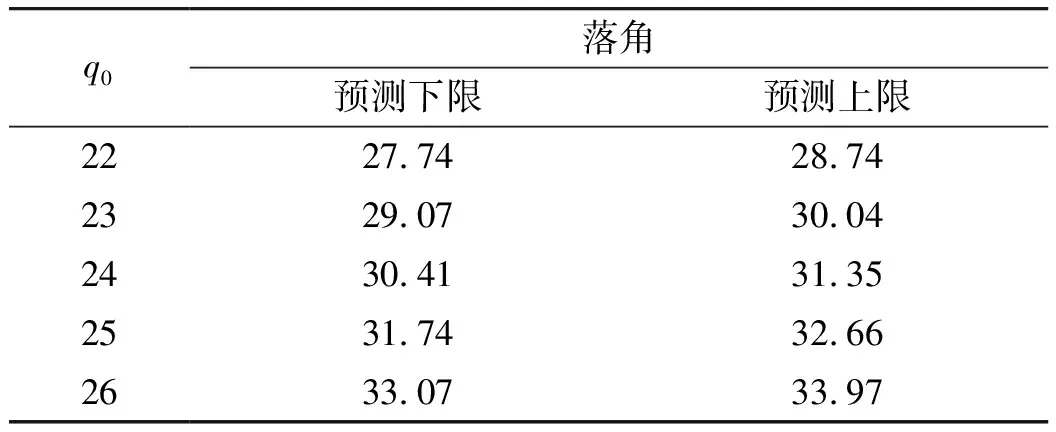
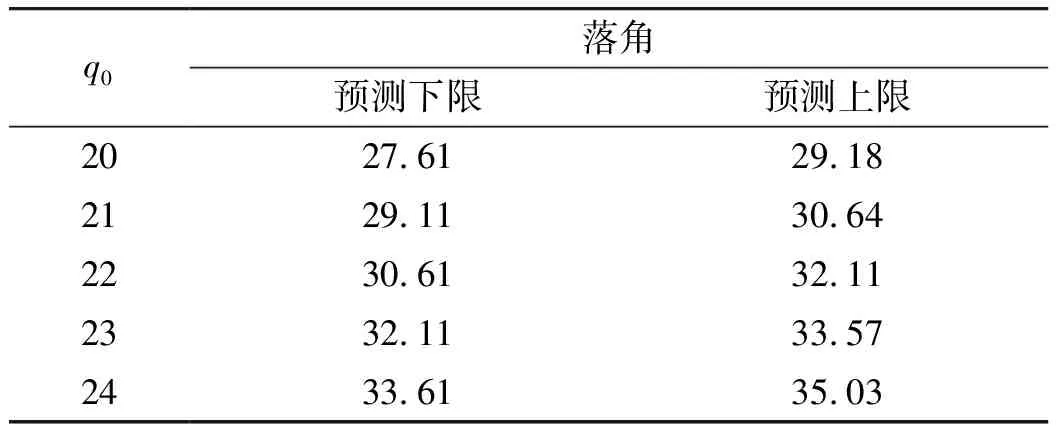
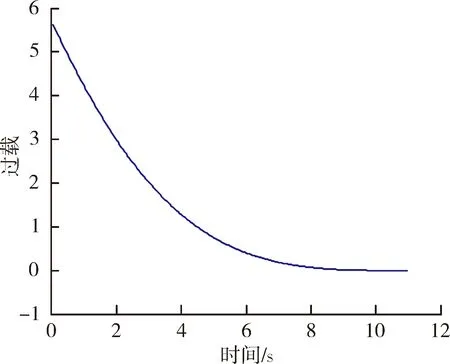
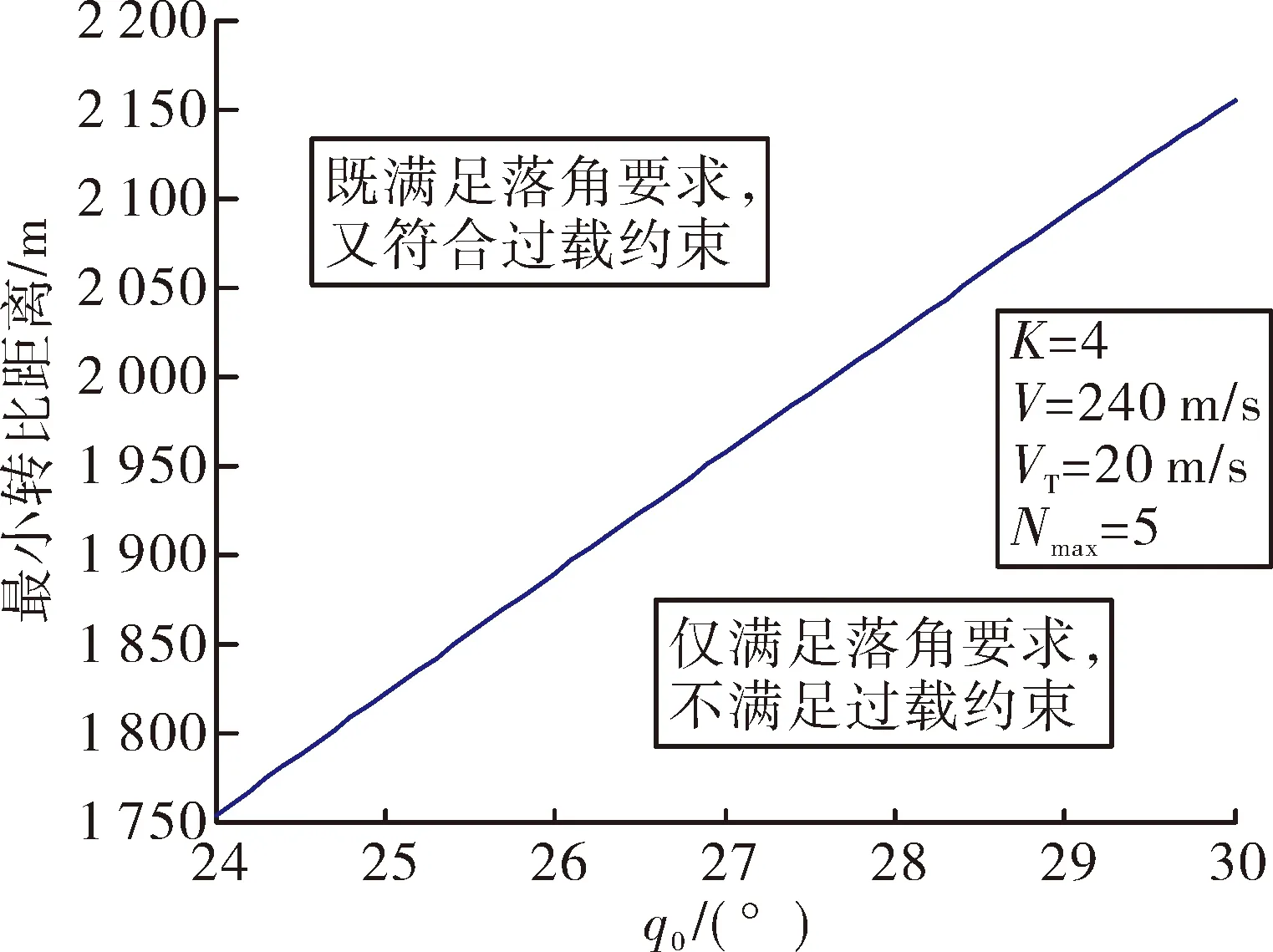
sinq0 (10) 將式(10)代入式(9)中,能得到Δq的取值范圍為: Δqmin<Δq<Δqmax (11) 這兩個端點數值均可以根據已知數據求出,當導彈從平飛轉到比例導引的時候,平飛段的速度前置角η0正好等于開始轉比的初始目標線角q0,所以Δq僅與比例系數K、速度比p、初始目標線角q0有關,可以看成這3個參數的函數: Δq=f(K,p,q0) (12) 首先確定速度比p,考慮到坦克機動的影響,設坦克分別以20 m/s的速度和-20 m/s的速度勻速前進,畫出這兩種彈道曲線如圖3所示。 圖3 不同速度比的彈道曲線對比 圖3中紅點是坦克初始位置,綠線是坦克前后兩種運動軌跡,綠圈是以坦克初始位置為圓心,以坦克最大速度20 m/s行駛時,在導彈命中目標大約5 s內所能到達最遠的圓。分析可得,當坦克迎面向導彈前進時落角更易滿足30°的約束,當坦克背離導彈前進時落角最難達到30°約束。所以只需要讓最難滿足落角約束的情況滿足條件,那么其他情況(坦克無論向什么方向以多大速度均可)都會滿足條件。所以之后將坦克速度按+20 m/s進行模擬。 假設導彈速度240 m/s,坦克速度20 m/s,坦克沿直線全速逃離導彈的情況下,初始r0=2 400 m,q0=30°,V=240 m/s,VT=20 m/s,K=4,根據數值進行仿真計算得出表1結果。 表1 仿真實例 (°) 當比例系數K不變,速度比p不變,可以根據不同初值q0求得最終目標線偏轉角的范圍,見表2。 表2 K=4,p=12時的落角預測 (°) 由表2可知,當要求滿足落角大于30°約束時,初始目標線角應大于24°,這樣最終加上最小偏轉角Δqmin后為30.4°,滿足落角約束條件。 表3 K=3,p=12時的落角預測 (°) 由表3可以看出,當要求滿足落角大于30°約束時,初始目標線角應大于22°,此時加上最小偏轉角Δqmin后為30.6°,滿足落角約束條件。 將式(4)對時間進行求導,可得: (13) (14) (15) (16) (17) 因為η是從q0變化到0,逐漸減小,所以當η=0時,式(17)右端有最大值,比例系數K應大于右端最大值。 將η=0代入式(17)得到: (18) 圖4 導彈過載曲線 可以發現在最初始階段過載已經為5.6左右,超過預計的最大可用過載5。 將過載表達式(16)與法向運動方程(4)聯立可得: (19) 因為nk≤nmax,可知比例系數K有上限,即 (20) 式中:rmax=3 000 m(導引頭最大識別距離),g=9.8 m/s2,nmax=5,V=240 m/s,VT=-20 m/s,η=ηT=30°,經計算可得:K<4.712。 綜上,比例系數K的范圍應滿足公式 (21) 在過載約束下影響導彈的落角主要有兩個參數,一個是初始目標線角q0,另一個是轉比距離r0。考慮到落角指標可根據落角預測模型得到,并且由于導彈受到過載限制,轉比距離不能太小,所以在開始啟動比例導引時,需用過載要小于等于最大可用過載,則可以按照導彈最大可用過載來估算轉比距離。 由式(21)可得: (22) 在啟動比例導引之前,導彈保持平飛,所以在初始時刻η=ηT=q0,可以得到: (23) 根據公式可以得到啟動比例導引制導律的最小距離rmin,令比例系數K=4,nmax=5,經式(23)計算出最小轉比距離r0,由于在落角預測中當K=4時得到初始目標線角大于24°時會滿足最終落角要求,以初始目標線角q0為橫坐標,r0為縱坐標,畫出曲線如圖5所示。 圖5 K=4時最小轉比距離與q0的關系 在圖5藍色曲線左上方的點,表示既滿足落角要求,又符合過載約束的初始彈道參數,曲線右下方的點表示僅滿足落角的要求,但是不滿足過載約束。同理,可以畫出當比例系數K=3時的最小轉比距離r0與q0的關系,如圖6所示。 文中根據理論分析得出落角公式,并建立落角預測模型。在計算彈道之前,僅根據初始值即可估算出落角的大致范圍,對導彈平飛段的平飛高度有指導性的作用。在實例中結合過載約束,選取合適的比例系數K,得出導彈需用過載變化趨勢。在給定最大可用過載的前提下,得出轉比距離、初始目標線角之間的 關系,根據仿真圖找出既滿足的過載約束,又符合落角條件的參數r0及q0,同時以期望落角命中目標。該方法原理簡單,工程上容易實現。但仍存在一些問題,如沒有完全挖掘出導彈的潛力,該模型僅考慮了最難滿足的落角要求,即目標遠離導彈全速逃跑的情況,如果不是該情況,那么落角會更大,將會得到更好的擊頂效果,這樣會造成導彈性能的浪費。 圖6 K=3時最小轉比距離與q0的關系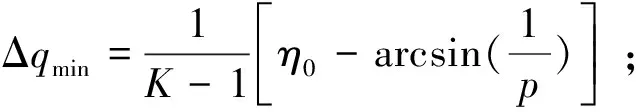

1.5 比例系數K的范圍
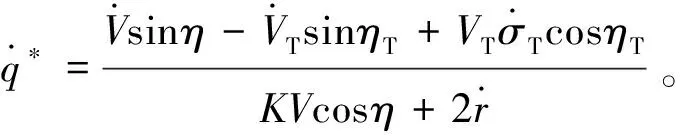
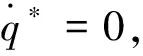
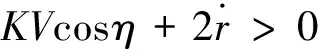
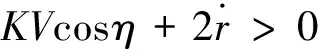
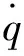
1.6 滿足戰技指標的初值范圍
2 小結