周期性自發調節下非線性經濟周期模型動力幅值分析
文/趙君,1.天津外國語大學英語學院國際商務系;2.“一帶一路”天津戰略研究院
1 引言
隨著世界經濟發展呈現繁榮、衰退、蕭條、復蘇周期性發展現象,使人們逐步認識到經濟系統受到多種復雜因素影響,不再是一個簡單的線性經濟系統。目前,關于經濟周期已形成了頗為豐富的理論,成為了宏觀經濟學研究的重要分支。對于非線性經濟周期模型的研究已成為近年來經濟周期理論研究的熱點問題,揭示了不同復雜條件下非線性經濟周期模型經濟指標演變規律與控制因素,提出了宏觀調控市場經濟活動的原則與措施,研究成果顯著。本文結合Goodwin 經濟周期模型與Puu 非線性經濟周期模型,以諧波函數作為模型的自發函數,建立了周期性自發調節下非線性經濟周期模型。
2 周期性自發調節下非線性經濟周期模型
結合Goodwin 經濟周期模型與Puu 非線性經濟周期模型,投資函數假定為自發投資、前期收入相關的函數
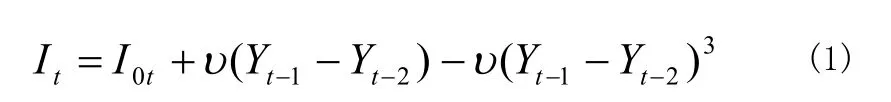
其中,It為現期投資;I0t 為自發投資;v 為資本-產出率,一般情況考慮v>0 的情況。Puu 采用前兩個時期收入差一次與三次方形式,模擬政府對公共基礎設施投資的反周期性。
同時,消費函數假定自發消費、補充儲蓄率和前期收入相關的函數

本文采用李佼瑞的方法將差分方程轉換為微分方程進行研究經濟周期的動力響應。此三種函數形式可以模擬不同的經濟環境影響。采用周期函數可以模擬經濟活動按照一定的周期規律自發調節,如下式所示

其中,q為投資強度系數,ω為自發調節變化頻率。
3 隱式增量諧波平衡法
本文采用一種隱式增量諧波平衡法研究周期性自發調節下非線性經濟周期模型動力幅值變化規律。當傅里葉級數選取適當的項數,所獲得周期解與式(3)的精確解符合良好。
收入Y展開為帶有N 項諧波函數和的形式

將式(4)代入式(3)將產生很多余弦函數與正弦函數乘積形式。將相同頻率倍數的余弦函數與正弦函數進行同類項合并,并將同類項系數表達式等于0,便獲得了m項帶有am 與ω的非線性代數方程,

當收入Y包含有較多項余弦函數與正弦函數時,求解式(5)每一項代數表達式是一項費時費力的工作。本文采用Cheung 和Iu 提出的一種隱式諧波平衡法進行計算機編程求解。
式(5)的非線性代數方程的殘差可以通過對式(3)逐項推導獲得。將式(4)代入式(3),逐項推導如下
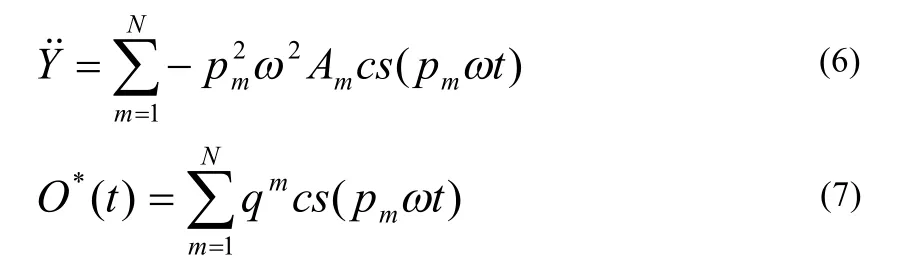
采用諧波平衡法,將以上表達式中相同cs(pmωt)的系數合并,歸到式(5)的第m項殘差中。對于收入Y 的時間導數,由于諧波函數的導數仍為諧波函數形式,所以引入相應標引參數計算余弦函數與正弦函數的求導結果,

其中,標引參數αm不但記錄了求導余弦函數與正弦函數的正負性,而且也記錄了求導后的項歸為哪項諧波函數的系數代數表達式。
對于項,表達式為

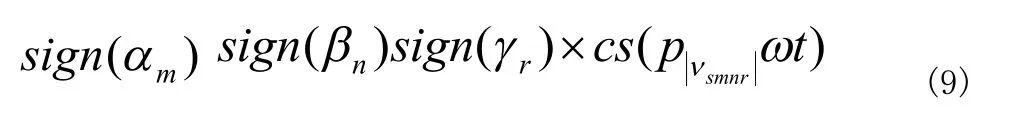
其中,βn,γr,vsmnr都為標引參數,與αm 的作用相同。具體三次余弦函數與正弦函數乘積表達式展開如下
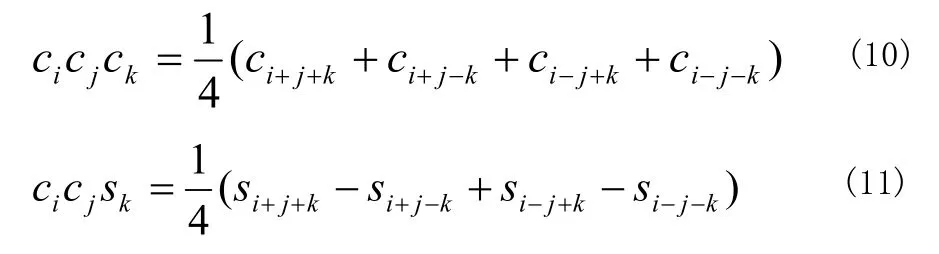
其中,ci= cos(iωt),si= sin(iωt)。
在對相同頻率倍數的余弦函數與正弦函數進行同類項合并后,獲得包含有A1,...,Am,ω變量的m個非線性代數方程組,將式(3)解的變化規律求解出來。本文采用Lagrangian 公式進行非線性代數方程組解的外推求算。設定式(3)解的曲線弧長s為非線性求解參數,向量A 包含有未知解A1,...,Am, ω,采用二次外推求解每個非線性代數方程組的解,即l=2,則有
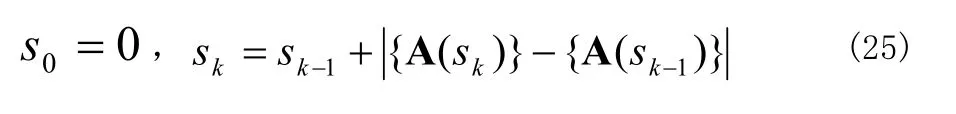
初始解可以選擇小振幅的線性自由振動的解。在追蹤變化頻率與振幅關系曲線式時,可以在小振幅可能出現的區間設定初始解。如果有多條變化曲線時,可以設定初始解并改變增量的正負性獲得不同的變化曲線。
4 結論
本文結合Goodwin 經濟周期模型與Puu 非線性經濟周期模型,以諧波函數作為模型的自發函數,建立周期性自發調節下非線性經濟周期模型,采用一種隱性增量諧波平衡法對周期性自發調節下非線性經濟周期模型動力幅值演變進行了數值分析。收入周期解假設為由正弦與余弦函數的組成的傅里葉級數形式。

