北京大興國際機場線160 km/h剛性接觸網系統弓網耦合受流質量分析

杜智恒

(1.北京市軌道交通建設管理有限公司,100068,北京；2.城市軌道交通全自動運行系統與安全監控北京市重點實驗室,100068,北京//工程師)

目前，剛性接觸網的適應速度已從最初的60 km/h，發展到了目前北京大興國際機場線(以下簡為“大興機場線”)的160 km/h。運行速度的大幅提升帶來了弓網受流關系的改變，致使弓網受流質量成為城市軌道交通供電系統的研究熱點。影響弓網受流質量的因素有很多，包括受流的直接部件剛性接觸網和受電弓的參數，以及設備材質、施工質量、設計參數、列車運行參數等[3]。這些因素不僅關系到弓網受流質量，同時也制約著剛性接觸網弓網性能的提升。諸多影響因素的存在，使得弓網受流質量一直成為學術研究的重點以及實際運行的難點。目前，計算機模擬法已成為研究剛性接觸網系統的常用方法[5]。

本文結合大興機場線現場實際數據、場景與工況，在建立剛性接觸網有限元模型與弓網耦合模型的基礎上，著重分析了剛性接觸網參數中的接觸網坡度、懸掛結構等效剛度、懸掛結構等效質量，以及受電弓參數中的弓頭質量、阻尼、剛度對弓網受流質量的影響，并針對大興機場線提出了優化措施。

1 弓網受流質量評價體系

1.1 弓網受流質量評價標準

弓網接觸壓力能夠準確地體現弓網間的接觸情況，以及直接地反映弓網受流質量[6]。目前可參考IEC 62486—2017來設定弓網間接觸力的最大值、最小值、平均值及標準差，并以此作為弓網受流質量的評價標準。

1.1.1 平均接觸力

接觸力平均值Fm反映列車運行時弓網間接觸力的整體狀況，其值按下式計算：

(1)

式中:

Fi——受電弓和接觸網間i處的接觸力；

n——總共采集的點數。

1.1.2 接觸力標準偏差

接觸力標準差σ表示弓網間接觸力的整體波動情況及弓網間接觸力的離散程度，是評價弓網受流質量的主要指標[7]，其值按下式計算：

(2)

1.1.3 接觸力的最大值與最小值

接觸力過大會使受電弓滑板和接觸線磨耗增大，因此接觸線和受電弓滑板需要經常更換，以縮短其使用壽命。弓網間接觸力過小會使弓網間的接觸電阻變大、弓網能耗增加，以及接觸線和滑板發熱嚴重。當接觸力小到一定程度時，會出現弓網離線現象，造成拉弧、灼傷接觸線與受電弓滑板，且損壞處后期會進一步加劇，導致弓網受流質量進一步惡化。

1.2 弓網受流質量案例選取

為使試驗結果更加真實地反映實際運行環境，以及為使試驗結果可靠性更高，本文選取大興機場線作為仿真案例。設定地下線和U型槽線路總長為21.981 km，列車運行時速為160 km/h；接觸網懸架方案為架空剛性接觸網，跨度為8 m，接觸線類型為CTAH120(高強度銅銀合金)，標稱電壓AC 25 kV。單側腕臂安裝如圖1所示。

圖1 單側腕臂安裝示意圖

1.3 弓網耦合動力學模型

列車行進時，受電弓沿著接觸線移動，接觸線與受電弓的相對位置、接觸狀態和整個弓網系統的剛度隨之變化，所以弓網耦合系統屬于時變系統，需用非線性理論和動力有限元方法進行分析。

非線性理論體一般體現在3個方面，分別為材料非線性(塑性、超彈性、蠕變等)、幾何非線性(大應變、大撓度、應力剛化等)和狀態改變非線性(接觸、單元死活)。隨著列車的行進，受電弓的位置不停地變化，導致弓網系統動力方程中的剛度矩陣亦不停地發生改變。所以本次研究可以定義為狀態改變非線性接觸。

在建立單元體的力學關系式時，除靜力作用外，還需考慮動荷載以及慣性力和阻尼力的作用。通過引入這些影響因素，建立單元體和整個體系的動力基本方程，并采用動力有限元法進行求解。其基本步驟為：①將有限元模型的連續區域進行離散化；②構造插值函數；③建立結構體系的運動方程；④求解運動方程；⑤計算結構的應力、應變和位移。

本文研究的動力學模型建立在受電弓與接觸網的耦合狀態下，在有限元軟件中通過建立“接觸對”來實現，即一個目標單元和一個接觸單元構成一個“接觸對”，程序通過一個共享的實常數號來識別接觸對。“接觸對”相當于在兩個物體間設置了一個彈簧，接觸力等于接觸剛度與穿透的乘積。但“接觸對”又不等同于彈簧，當兩物體分開時，接觸剛度不起作用。研究弓網耦合關系，首先需建立弓網間的剛度關系，弓網接觸剛度表征了弓頭為抵抗接觸線垂直移動而產生彈性變形的能力。

對于剛性懸掛而言，接觸線在受電弓頂升作用下產生一定的變形，受電弓弓頭本身相對接觸線而言變形很小，故可設置接觸線為柔性、弓頭為剛性。由有限元軟件中凸、凹面接觸時目標面和接觸面的指定規則，指定接觸線為目標面、弓頭為接觸面。

2 剛性接觸網參數對弓網受流質量的影響

2.1 剛性接觸網坡度對弓網受流質量的影響

城市軌道交通中的列車運行環境較為復雜，由于受到當地條件、施工條件及后期維護條件的影響，接觸線并不能保證能夠始終處于水平位置。同時，城市軌道交通線路運行環境的改變，勢必造成接觸網坡度發生變化，坡度變化的幅度δ可表示為：

δ=(Ha-Hb)/L

(3)

式中：

Ha——錨段始端垂直高度；

Hb——錨段末端垂直高度；

L——錨段長度。

在仿真試驗中，為更好地探究坡度變化對弓網受流質量的影響，設定坡度變化范圍為0～5‰，增長幅度為1%。仿真結果如圖2所示。

圖2 接觸網坡度對弓網接觸力影響情況

從圖2可見，F隨坡度的增加呈遞減趨勢，Fm隨坡度增加呈下降趨勢，下降速率與坡度的增加速率并無明顯關系；Fmax和Fmin隨坡度增加降低程度不斷增加，其中Fmin的變化較為明顯，甚至出現Fmin=0的情形;σ隨著坡度增加不斷擴大，表明接觸網坡度會影響弓網間受流質量。坡度和弓網的受流質量呈反比,當坡度為2‰～3‰ 時Fmin為9.945 N，小于行業標準中的30 N。在考慮設計預留的情況下，需將機場線坡度控制在1‰以下，以保證列車運行過程中穩定可靠地受流。

2.2 懸掛結構等效剛度對弓網受流質量的影響

腕臂底座安裝高度及調節螺栓能夠在一定范圍內對接觸網的垂直距離進行調節，以此來降低接觸線和軌道的坡度。但調整的幅度受角度不斷變化的影響，調整幅度的不同使得剛性接觸網懸掛結構的等效剛度(復雜結構進行有效歸算)亦發生相應變化，從而影響弓網受流質量。為探究等效剛度的影響結果，改變懸掛結構的等效剛度，分析弓網間動態接觸力指標的變化，結果如圖3所示。

從圖3可以看出，懸掛結構的等效剛度對F的影響很小；反之，當懸掛結構等效剛度不斷減小時，F參數得到一定改善，表明弓網受流質量得到改善提升。因此，北京新機場線在設計與施工過程中，調節螺栓可在0.01～1.00倍等效剛度間適度調整，以提高弓網受流質量。

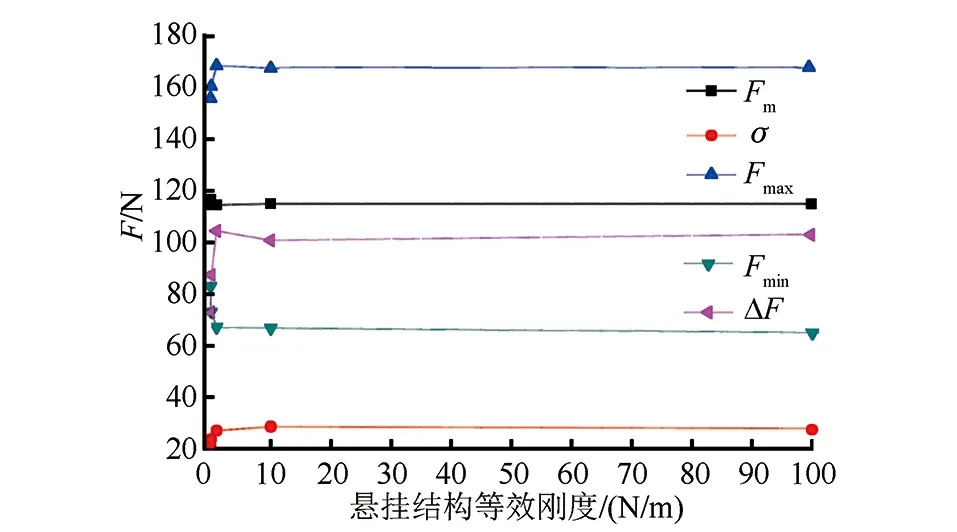
圖3 懸掛結構等效剛度對弓網間接觸力的影響曲線

2.3 懸掛結構等效質量對弓網受流質量的影響

不同類型懸掛結構的材質、質量影響著懸掛結構的等效質量。為探究等效質量的影響結果，懸掛結構等效剛度不變，在原有懸掛結構等效質量的基礎上，分別進行10%和20%的上下浮動，分析F的變化，結果如圖4所示。

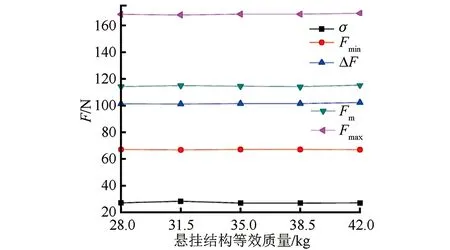
圖4 懸掛結構等效質量對弓網間接觸力的影響曲線

從圖4可以看出，無論等效質量增加還是減小，當其處于20%的變化幅度范圍之內時，Fm、Fmax、Fmin、ΔF和σ均未發生明顯改變，說明等效質量在一定范圍內的變化并未對弓網受流質量產生影響。

3 受電弓參數對弓網受流質量的影響

弓網受流過程中，受電弓弓頭滑板與接觸線之間的接觸處于動態變化中，在一定程度上影響著弓網受流質量。因此，應著重探究受電弓弓頭的參數對弓網受流質量的影響程度。

3.1 受電弓弓頭質量對弓網受流質量的影響

為增加仿真結果的通用性，以及為更全面地分析受電弓弓頭集總質量對弓網間動態接觸力的影響。以原質量為16.12 kg的Stemmann DSA380D型受電弓為設定標準，分別對受電弓弓頭集總質量設定為原質量的0.8、1.0、1.2、1.5、2.0、4.0倍，分析F的變化，結果如圖5所示。

從圖5可以看出，弓頭集總質量的增加，對于Fm影響較小，但是對Fmax和Fmin的影響卻較為明顯，這導致F的變化幅度變大，弓網受流質量受到影響。當弓頭集總質量適當減小時，F的變化幅值與σ的降低幅度較為明顯。因此，大興機場線在進行受電弓選型過程中，盡可能選取弓頭集總質量為14.98 kg左右的Panto420型新型受電弓，以提升弓網受流質量。

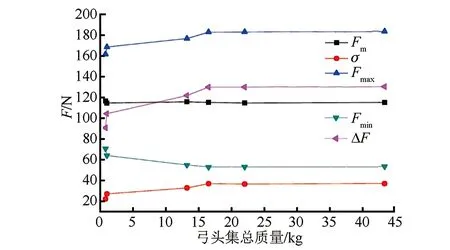
圖5 弓頭集總質量對弓網間接觸力的影響曲線

3.2 受電弓弓頭阻尼對弓網受流質量的影響

實際運行中，受電弓滑板與接觸線的振動是不可避免的，但是可以通過調節受電弓的弓頭阻尼降低振動。在仿真分析中，其他參數設定不變，設置受電弓弓頭阻尼分別為0 Ns/m、30 Ns/m、60 Ns/m、90 Ns/m、120 Ns/m和150 Ns/m，來分析弓網動態接觸力的變化，結果如圖6所示。

從圖6可以看出，受電弓弓頭阻尼為90 Ns/m是F指標參數的分水嶺。當弓頭阻尼為0～90 Ns/m，且當其不斷增大時，Fmax和Fmin數據得到優化，說明弓網受流質量得到提升改善；當弓頭阻尼為90～150 Ns/m，且當其不斷增大時，F的變化趨勢與前述相反，說明弓網受流質量降低。因此，將弓頭等效阻尼設定為90 Ns/m左右，可以較好地保證弓網受流質量。

圖6 弓頭阻尼對弓網間接觸力的影響曲線

3.3 受電弓弓頭剛度對弓網受流質量的影響

弓網系統中，懸掛結構等效剛度是影響弓網受流質量的因素之一。為更全面地分析受電弓弓頭剛度對F的影響，分別將受電弓弓頭剛度設定為原弓頭剛度的0.6、0.8、1.0、1.2、1.4倍，其他參數設定不變，分析F的變化，結果如圖7所示。

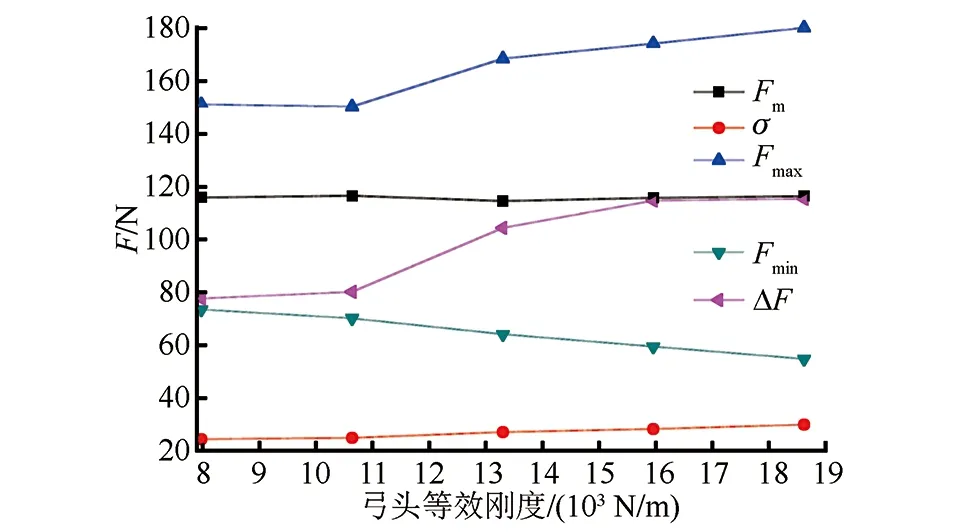
圖7 弓頭等效剛度對弓網間接觸力的影響曲線

從圖7可以看出，F與受電弓弓頭剛度間的變化關系較為明顯，隨著受電弓弓頭剛度增加，Fm并未發生明顯變化，但是對Fmax和Fmin影響很大，增加了弓網之間的波動幅度，造成F的變化幅值增加；通過變化趨勢可以看出，受電弓弓頭剛度的增加，降低了弓網受流質量。

4 結語

通過設定弓網受流質量標準，選取大興機場線作為工程案例，研究剛性接觸網參數及受電弓參數對弓網受流質量的影響，并以此為基礎為大興機場線的設計與施工提出合理化優化建議，從而在一定程度上提升了弓網受流質量，為保障該路線穩定、可靠運行提供重要的理論參考。