主題聚焦漸次展開微型專題精準備考

劉東升 王俊蓉

最近一次跨地區（江陰市與海安市）初中數學教研活動上，我們把研討主題確定為中考微專題，讓專題復習的主題更加聚焦。由于承辦地安排在江陰，為了貼近無錫地區中考風格，我們共同打磨研發了一節關注綜合題中“直線表達式”的求解專題復習課。本文先簡要整理該課的教學設計，再給出教學立意的相關闡釋，以供分享和研討。

一、綜合題中“直線表達式”的求解專題復習課

活動1 自主先練，開課交流。

問題1 已知，平面直角坐標系xOy中，直線y=kx+b經過A，B兩點。

（1）若點A（6，0），B（0，4），求k，b的值;

（2）若點A（[133]，0），B（0，[132]），求k，b的值;

（3）若點A（0，0），B（[72]，[32]），求k，b的值;

（4）若點A（3[5]，5），B（0，-1），求k，b的值。

教學組織：這組練習可安排學生課前完成，開課之后就進行板演或投影，引導學生互評解答。

設計意圖：已知兩點坐標求解直線表達式，考查的是基本運算能力。課前安排學生先練，節約了課堂復習時間，并且這4個運算求得的結果，分別對應著本課后續一些綜合題中的解答，能讓學生在后續復習活動中把更多的精力用在思路分析與解法優化上。

活動2 旋轉變換后求正比例函數的表達式。

問題2 已知，平面直角坐標系xOy中，點A（2，[3]）。在射線OA上任取一點P（m，n），其中m，n為正實數，過點P作PH⊥x軸，垂足為H。

（1）直接寫出直線OA的表達式，并用含m的式子表示n。

（2）將PH繞點P逆時針旋轉60°到PQ的位置，點H與點Q為旋轉前后的對應點。求直線OQ對應的函數表達式。

教學組織：安排學生先根據題意構造草圖分析，并先解決第（1）問，處理第（2）問時分析Q點的坐標。學生可能會構造圖1進行分析。可安排學生上臺講解思路。在此基礎上跟進一道變式習題。

圖1? ? ? ? ? ? ? ? ? ? ? ? 圖2

變式：如圖2，平面直角坐標系xOy中，將直線y=[12]x繞原點逆時針旋轉45°后所得直線對應的函數表達式是__________。

教學組織：安排學生先畫圖分析，解題的關鍵是分析出旋轉后直線上某個特殊點的坐標，然后就可確定直線表達式。

設計意圖：這個活動及變式的立意主要是讓學生感受在平面直角坐標系中分析旋轉變換后某點的坐標，是確定過這點與原點的直線表達式的關鍵。

活動3 求綜合題中直線對應的函數表達式

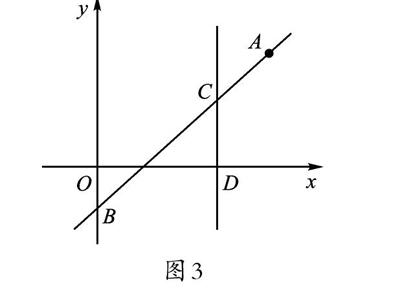
問題3 已知，如圖3，一次函數y=kx-1的圖像經過點A（[35]，m）（m>0），與y軸交于點B，點C在線段AB上，且BC=2AC，過點C作x軸的垂線，垂足為點D。

（1）當CD=2時，求直線AB對應的函數表達式;

（2）小江設計一個問題：若AC=CD，求直線AB與x軸交點的坐標。你覺得“小江問題”該如何解決？請思考后先在小組內交流大致思路或解題方向，再演算求解。

圖3

教學組織：（PPT漸次呈現）教師提問，“你能讀出哪些信息？”學生在小組內交流分享個人理解，然后PPT再漸次呈現后續兩個小問。在學生獨立思考演算解答之后，再安排學生上臺講解。

設計意圖：這個題組改編自無錫地區中考綜合題，將其中關鍵步驟分解、重組成這一問題串，以幫助學生訓練中考較難題中的關鍵一步。

活動4 求“位置不定”的直線對應的函數表達式

平面直角坐標系xOy中，已知原點O、點A（a，0）、B（0，b）、C（6，4）四點在同一個圓上，其中a，b為正實數。

教學組織：先PPT呈現，請設計一個問題并求解，然后小組內交流。

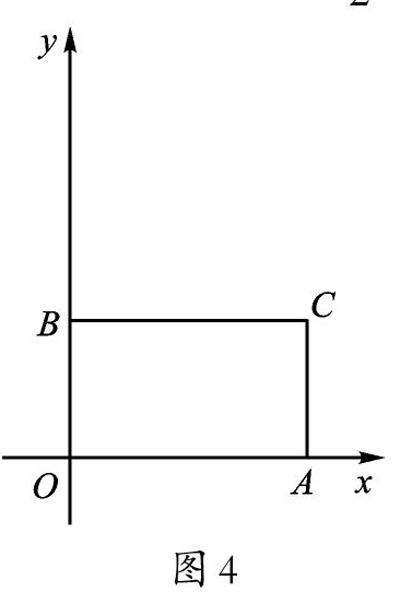
教學預設：∠ACB=90°;求tan∠ABC的值為[23];再比如增設“如圖4，當四邊形AOBC是矩形時”，還可繼續引導學生探究它的外接圓的直徑是[213]，半徑是[13]等。目的是為了引出較難的一道挑戰題。

挑戰：連接AB，AC，BC，當△ABC與△AOB的面積相等時，求直線AB對應的函數表達式。

教學預設：學生可能會容易想到四邊形AOBC是矩形的情況（如圖4），這時可求出直線AB對應的函數表達式為y=-[23]x+4;另一種情況（如圖5）是作線段OC的垂直平分線，與x，y軸的交點就是符合要求的點A，B。此時直線AB對應的函數表達式是y=-[32]x+[132]。

? ? ? ? ? ? ? ? ? 圖4? ? ? ? ? ? ? ? ? ? ? ? ? ?圖5

課堂小結：

1.在綜合題中涉及求直線對應的一次函數表達式，你覺得有哪些經驗值得分享？小組內分享，可以結合本課中提到的一些題例分享各自的經驗。

2.這節課主要復習綜合題中涉及一次函數表達式的求解;無錫考卷中的一些中考真題有哪些呢？布置三道作業，2017年無錫中考試卷第25題，2018年的第26題、第28題。

二、教學立意的進一步闡釋

第一，專題突破，讓復習主題更加聚焦。

就我們在學校聽課所見，多數中考專題復習課仍然沿襲著“開放題”“規律探究題”“閱讀理解問題”“運動變化問題”等專題分類方式。以上述專題分類，只是從試題的“外形”上進行劃分，似乎有一定的道理，但從具體來看，這些“形似”的專題放在一起，很可能它們涉及的知識點、解題策略卻是“各不相同”的。這樣的專題復習課難免會“七零八碎”，復習效益難有提升。我們提出中考微專題的復習追求，比如上文課例中主題關注綜合題中的直線表達式的求解，就是從“形似”走向“神似”，將那些解題策略相近、涉及知識點相近的習題聚集在一起，串珠成線，提煉主線，讓復習主題更加聚焦，追求專題復習效益的顯著提升。

第二，貼近中考，讓復習選題更加精準。

從上文課例中的選題可以看出，我們在不同“活動”下預設的系列問題都改編自無錫地區的中考真題，這也是最后布置作業時提到這些考題的原因。目前江蘇的中考都是各大市獨立命題，每個地區中考試卷都有明顯的地區風格或“考查喜好”。我們研究了近三年無錫中考最后三道綜合題，在這些題中都涉及確定直線表達式的考查要求，這也是我們研發這節微專題的主要用意。中考備考，時間緊、任務重，如何精準備考、高效備考，我們認為貼近地區中考命題風格的選題復習才是精準有效的。那種盲目選取外地“無關”考題的所謂鏈接中考是要不得的，浪費學生寶貴的復習時間，得不償失。

第三，預設鋪墊，讓較難問題漸次展開。

由于本課選題的來源是近幾年無錫中考綜合題，雖然進行了改編、刪減，聚焦了綜合題中直線表達式的確定，但是課堂教學時間還是偏緊，如果只是呈現“原生態”的考題，學生就更難在一節課中突破幾個較難問題。所以，我們在課前就針對這些較難題預設了鋪墊式問題，比如“活動1”就是后續三個活動的鋪墊，讓學生課前先把一些基本運算都解決掉;再比如“活動3”中綜合題本來要分類討論，但我們通過開放式設問、跟進追問，在較難題呈現前已有了必要的鋪墊，比較優秀的學生就能循著前面的問題，較順利地獲得思路和解答，既節約了課堂教學時間，也給了學生求解較難題的思路啟示，這是通過“學習解題”達到幫助學生“學會解題”的一種追求。

（作者單位：①江蘇省海安市城南實驗中學;②江蘇省江陰市教師發展中心）

【參考文獻】

[1]劉東升.中考專題復習課：求聯求變讓老歌新唱——以中考“二次三項式再認識”復習為例[J].中學數學，2019（2）：54-55，60.

[2]劉東升. “形散神聚”的主題，“淺入深出”的環節——中考二輪微專題復習課“無處不在的邊角關系”教學流程與立意[J].教育研究與評論（中學教育教學），2018（04）：87-91.

[3]劉東升.“開放”需要“放開”，“對話”促進“生成”———“二次函數復習”展評課的設計、對話與思考[J].中學數學月刊，2012（11）：26-31.