具有3T、2T1R和2R1T模式的并聯(lián)機構構型綜合

劉 偉 劉宏昭

(1.西安理工大學機械與精密儀器工程學院， 西安 710048; 2.西安工程大學機電工程學院， 西安 710048)

0 引言

具有多種運動模式的并聯(lián)機構的特征為：較少的驅動副可以實現(xiàn)多種運動模式；運動模式變換時不需要對機構進行重新組裝，因而可以快速實現(xiàn)機構重構；一些此類并聯(lián)機構在進行運動模式變換時，需要通過機構的奇異位形[1]。

DOMY并聯(lián)機構具有4種不同的3自由度運動模式[2]，這種機構中含有特殊的運動鏈，HUNT[3]最早在研究連軸器時對其特征進行了分析。文獻[4]使用幾何代數(shù)方法[5]分析了此類具有運動分岔的機構所具有的運動模式類型。文獻[6-7]對單環(huán)機構運動分岔的特征進行了分析，將轉動軸線、移動方向的重合或平行作為機構運動模式變換的臨界條件，并基于此設計了具有多種運動模式的機構。文獻[8]對機構運動分岔時的奇異位形進行了分類，設計了一些具有多種運動模式的并聯(lián)機構[9]。文獻[10]綜合了實現(xiàn)3T、3R、2R1T、2T1R三自由度運動模式相互轉換的并聯(lián)機構。文獻[11-12]使用幾何方法討論了一些單環(huán)機構的運動分岔[13]問題。文獻[14]使用可重構轉動副設計了一種具有2R1T和3R運動模式的完全對稱并聯(lián)機構。文獻[15]使用虛擬運動鏈，先對不同運動模式的并聯(lián)機構支鏈進行型綜合，選擇兩種運動模式共有的支鏈結構作為可選支鏈，再結合不同運動模式支鏈裝配的幾何條件，綜合了具有多種運動模式的并聯(lián)機構。文獻[16]基于方位特征集，使用可變自由度支鏈、定自由度支鏈，綜合了具有兩轉兩平移和一轉三平移運動模式的并聯(lián)機構。文獻[17-18]基于位移流形理論，使用串聯(lián)變自由度支鏈綜合了具有兩移動一轉動和兩轉動一移動運動模式、具有兩轉動一移動和三轉動運動模式的并聯(lián)機構。具有2T1R運動模式的并聯(lián)機構在工業(yè)裝配機器人、姿態(tài)調節(jié)器、并聯(lián)機床等領域應用比較廣泛。具有3T運動模式的并聯(lián)機構在3D打印和分揀搬運等領域應用廣泛。具有2R1T運動模式的并聯(lián)機構，適合應用于在曲面上工作的操作手，具有剛度高、精確度高、靈巧性強等特點。

目前，具有多種運動模式的并聯(lián)機構并沒有被完全綜合出來，一些機構所具有的新型運動模式相繼被發(fā)現(xiàn)，具有多種運動模式的并聯(lián)機構綜合仍然是機構學研究的熱點之一。多運動模式的并聯(lián)機構在運動模式變換時，機構處于奇異位形，機構的自由度增加，對機構運動模式變換造成了困難。文獻[19]提出實現(xiàn)運動模式變換的方式：手動、動態(tài)通過、增加額外的驅動副。增加額外的驅動副可對機構進行控制，但過多的驅動副會增加機構的制造成本，并且增大了機構的控制難度。本文設計使用較少驅動副和支鏈，實現(xiàn)多種運動模式的機構，以期該類機構具有應對一定復雜工況的能力。

1 變自由度支鏈

1.1 串聯(lián)變自由度支鏈

一般情況下，并聯(lián)機構支鏈結構可以根據(jù)位移子群或位移流形的生成元得到。典型的變自由度支鏈uRv1RwPv2RaR支鏈，如圖1a所示，其位移流形可表示為

{R(A,u)}{R(v1)}{T1(w)}{R(v2)}{R(A,a)}

(1)

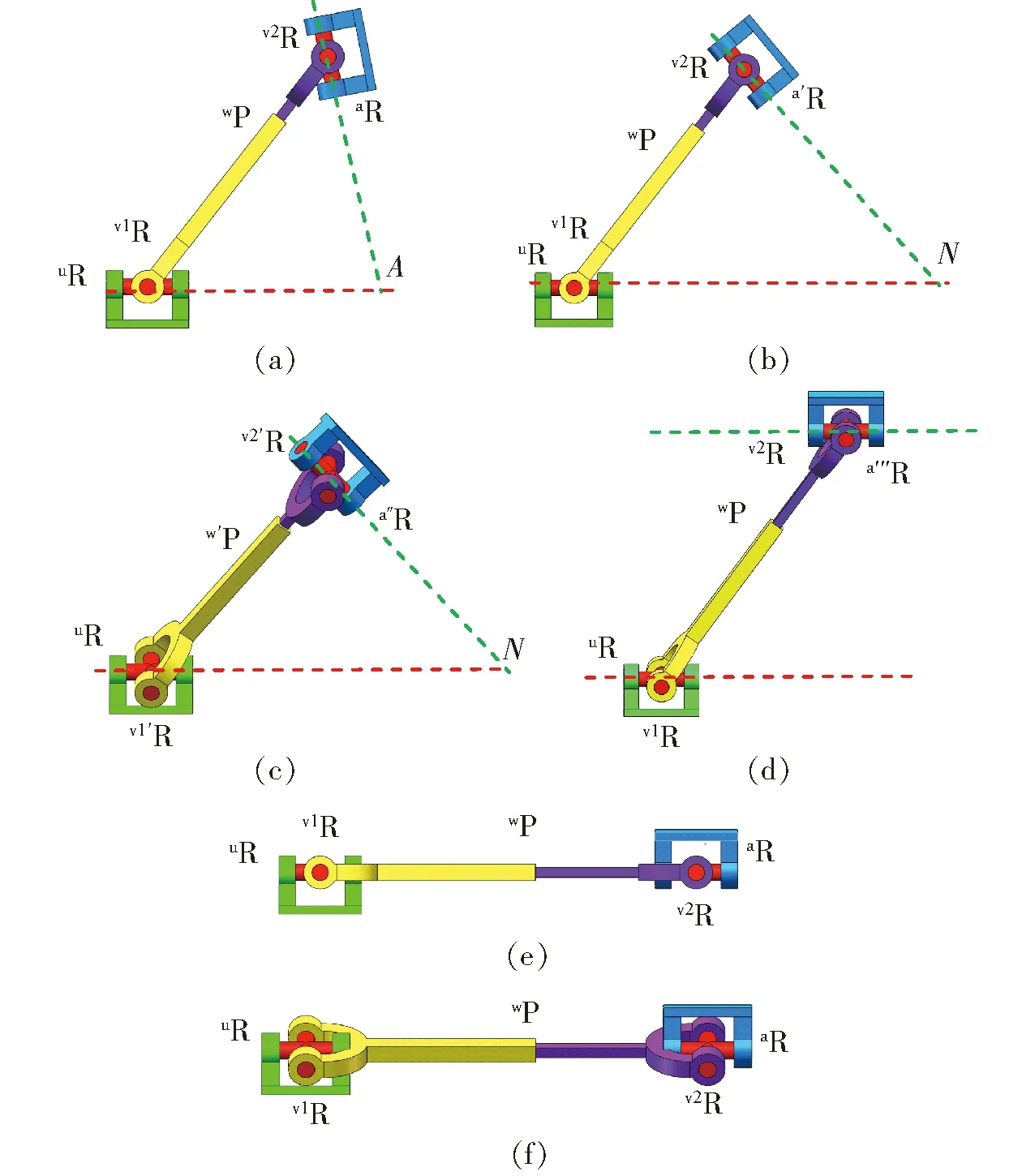
圖1 uRv1RwPv2RaR變自由度支鏈運動模式變換Fig.1 uRv1RwPv2RaR variable DoF branch chain motion mode transformation

當圖1a所示支鏈末端繞平行于轉軸v1R的軸線做有限轉動或沿移動副wP做有限移動后，轉軸aR與連接在定平臺上的U形副轉軸uR的交點，從圖1a中的點A移動到點N，此時支鏈位形如圖1b所示。當圖1b所示支鏈繞uR轉軸做有限轉動后，轉軸a′R與U形副轉軸uR的交點不變。轉動副v1′R、v2′R與它們相連接的移動副w′P和連接動平臺的轉軸a″R發(fā)生變化，如圖1c所示。當圖1b所示支鏈繞v2R轉軸做有限轉動后，轉軸a?R與轉軸uR平行，如圖1d所示。該支鏈位形下支鏈末端具有2個轉動自由度和3個移動自由度，支鏈末端受到1個垂直于萬向鉸鏈轉軸的約束力偶。當圖1d所示機構支鏈末端移動后，支鏈處于圖1e所示位形，支鏈中存在1個局部轉動自由度，支鏈末端姿態(tài)不變，支鏈1中的vRwPvR運動鏈可繞軸線uR轉動后，支鏈處于圖1f所示位形。從圖1支鏈位形的變化過程中可以發(fā)現(xiàn)，圖1a中的支鏈vRwPvR具有2個移動自由度和1個轉動自由度，由于支鏈中轉動副uR的轉動，vRwPvR子鏈的移動平面的法線v將會發(fā)生改變。并且，由于vRwPvR子鏈所具有的移動和轉動自由度，使得轉軸aR的軸線與轉軸uR的軸線的交點，在轉動副uR的軸線上產生移動。當該交點移動到無窮遠位置時，支鏈位形圖如圖1d所示。不同支鏈在移動、轉動運動求交集時，移動平面的法線方向和轉動中心起重要作用。圖1所示支鏈所具有的上述運動特性，使得以其作為支鏈的并聯(lián)機構可以實現(xiàn)運動模式的變換。

1.2 混聯(lián)變自由度支鏈

具有2T1R和2R1T運動模式的機構如圖2所示[17]，如圖2a所示，當定自由度支鏈B1A1中的轉動副R14的軸線l1與串聯(lián)變自由度支鏈B2A2的轉動副R24的軸線l2不平行時，該機構具有2T1R運動模式；如圖2b所示，當定自由度支鏈B1A1中的轉動副R14的軸線l1與串聯(lián)變自由度支鏈B2A2的轉動副R24的軸線l2平行時，該機構具有2R1T運動模式。圖2所示并聯(lián)機構的動平臺A1A2A3串聯(lián)移動副后，可得到混聯(lián)變自由度支鏈，支鏈末端具有3T1R和2R2T兩種運動模式，該支鏈結構如圖3所示。然而，移動副一般情況下不作為被動運動副，可以使用等效移動副對其進行替換。平面平行四邊形四桿機構可作為單自由度等效移動副，如圖4所示。

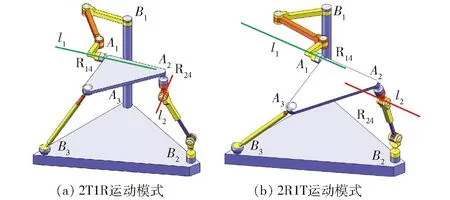
圖2 具有2T1R和2R1T運動模式的并聯(lián)機構Fig.2 Parallel mechanisms with 2T1R and 2R1T motion modes

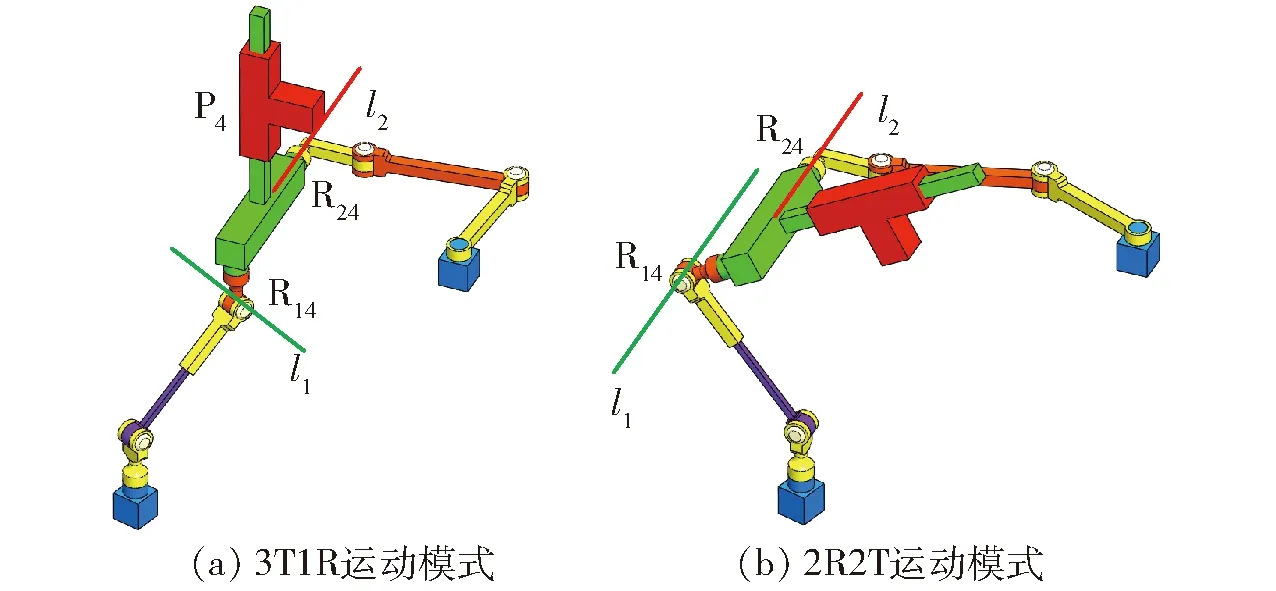
圖3 具有3T1R和2R2T運動模式的混聯(lián)變自由度支鏈Fig.3 Hybrid variable DoF branched chain with 3T1R and 2R2T motion modes

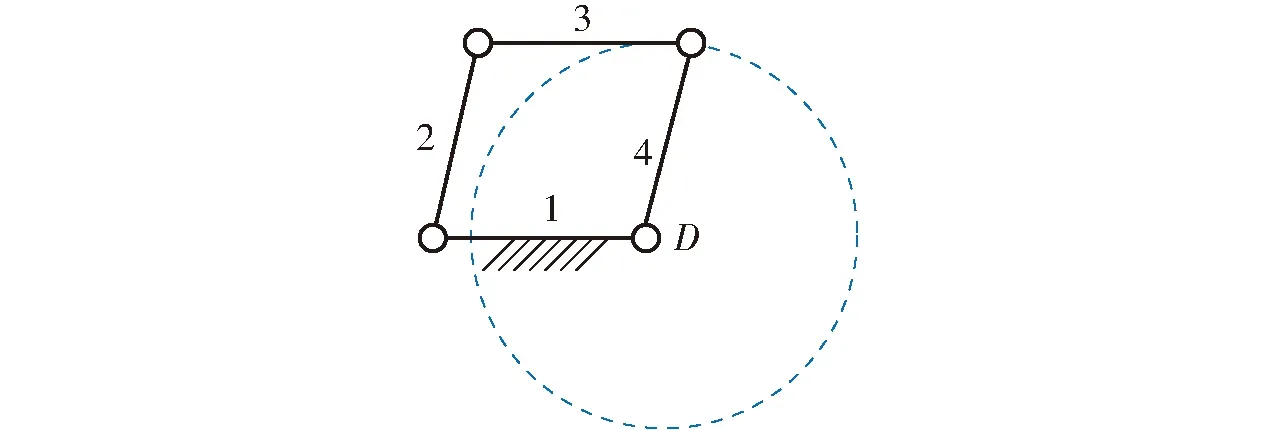
圖4 平面平行四邊形機構Fig.4 Planar parallelogram mechanism

圖4所示平面平行四邊形機構的連桿3繞圓心D沿圖中的圓進行移動，連桿3具有一維移動位移流形，其運動不具有群的結構。假設圖4所示連桿1上串聯(lián)兩個沿X、Y軸的移動副，連桿3在平面YOZ中進行一維圓周移動，連桿3的運動所具有的位移流形為

{T1(X)}{T1(Y)}{T1(YOZ)}

(2)

由于 {T1(X)}{T1(Y)}?T3

{T1(YOZ)}?T3dim({T1(X)}{T1(Y)}{T1(YOZ)})=dim(T3)=3

(3)

可得

{T1(X)}{T1(Y)}{T1(YOZ)}=T3

(4)

圖4中連桿1串聯(lián)2個移動副，且保證連桿3移動自由度與上述2個移動副運動獨立，則連桿3具有空間3維移動的運動模式。因而，將圖3中的移動副P4用圖4中的平行四邊形機構替換后，圖3a支鏈末端具有3T1R運動模式。當圖3b機構中的運動副P4用圖4中的平行四邊形機構替換后，圖3b支鏈末端具有2R2T運動模式，支鏈末端的移動曲面為圓周弧線沿直線移動形成的曲面，該移動運動模式不具有群的結構，為2維移動位移流形。

2 具有3T、2T1R和2R1T運動模式的并聯(lián)機構

當機構處于運動模式的變換位形時，機構瞬時自由度會增加，為了使用較少的驅動副，實現(xiàn)3T、2T1R、2R1T多種運動模式相互變換，應盡量避免機構同時具有3種運動模式時進行運動模式變換。當機構在2種運動模式之間變換時，改變1個自由度，則機構在變換位形自由度增加1個。如果機構運動模式自由度改變多于1個，則機構在變換位形自由度也會增加多個自由度，因而需增加多個輔助驅動副，來實現(xiàn)機構運動模式的變換，這增加了機構運動模式變換過程中機構的控制難度和機器設備制造成本。機構在3T、2T1R、2R1T運動模式間的變換路徑可以為：機構從3T運動模式運動到3T1R瞬時自由度變換位形，然后變換為2T1R運動模式，機構再從2T1R運動模式運動到2R2T瞬時自由度變換位形，最終變換為2R1T運動模式。機構從最初的3T運動模式變換到2T1R運動模式，機構3T運動模式的1個移動自由度變換為1個轉動自由度，機構在自由度變換位形下具有3T1R瞬時自由度，此時機構自由度增加1個。機構再從2T1R運動模式變換為2R1T運動模式，機構2T1R運動模式的1個移動自由度變換為1個轉動自由度，機構在自由度變換位形下具有2R2T瞬時自由度，此時機構自由度同樣增加1個。機構在運動模式變換時，始終自由度增加1個，理論上只需要1個輔助驅動副就可以實現(xiàn)機構運動模式的變換，這有利于降低機構運動模式變換的控制難度和機器設備的制造成本。可以通過設計非對稱結構的并聯(lián)機構來避免機構運動模式變換時，機構同時具有多種運動模式，造成機構自由度增多，需多個輔助驅動副來實現(xiàn)機構運動的控制問題。

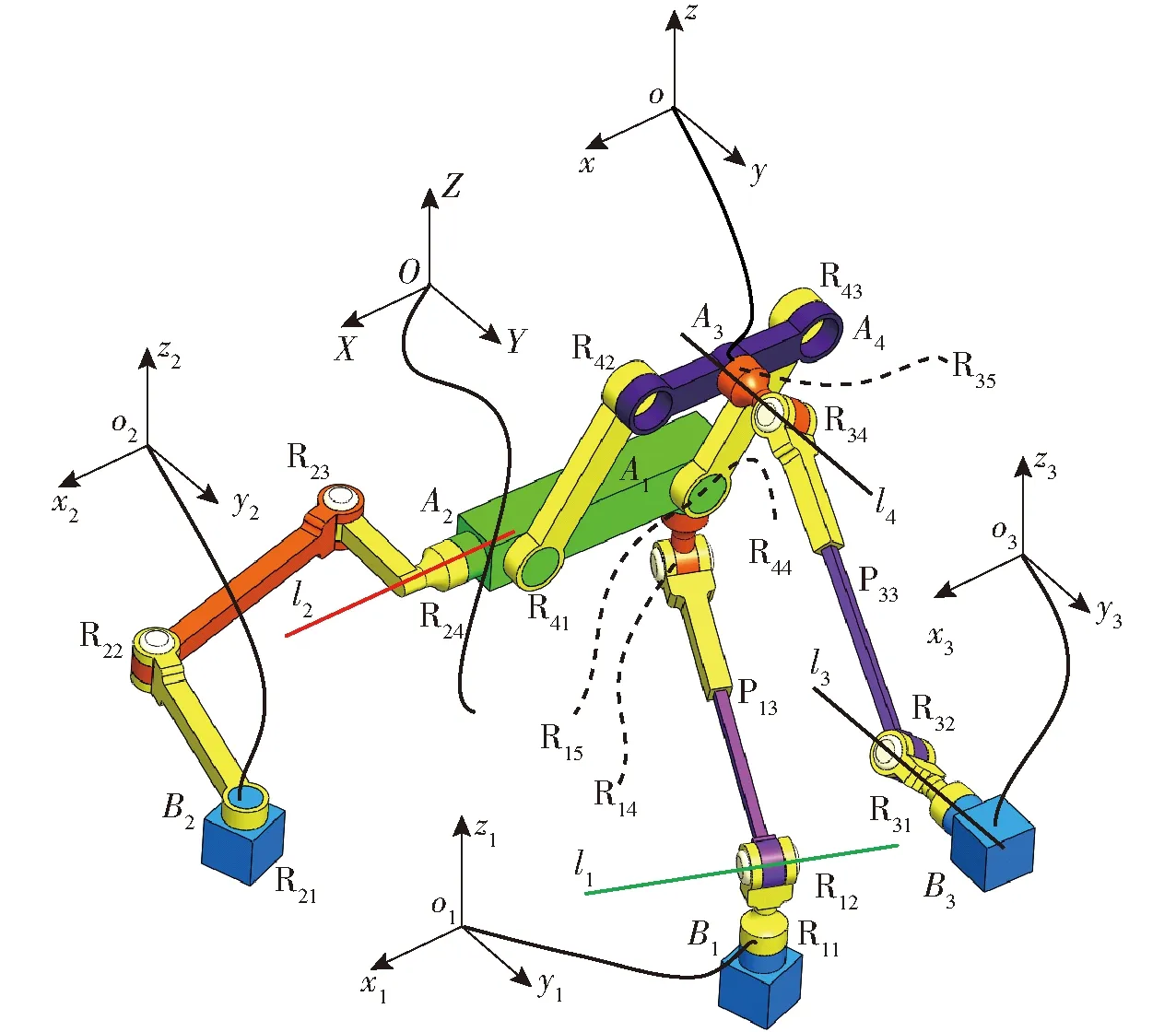
圖5 具有3T、2T1R和2R1T運動模式的并聯(lián)機構Fig.5 Parallel mechanisms with 3T, 2T1R and 2R1T motion modes

由于1.1節(jié)和1.2節(jié)中的串聯(lián)變自由度支鏈和混聯(lián)變自由度支鏈可以實現(xiàn)運動模式的變換，且都能實現(xiàn)3T、2T1R、2R1T運動模式，理論上可以使用該混聯(lián)變自由度支鏈和串聯(lián)變自由度支鏈來實現(xiàn)3T、2T1R、2R1T運動模式的變換。如圖5所示，定平臺為B1B2B3，動平臺為A3A4。連接B1與A1的運動鏈結構為ZRuRPuRZR，兩個轉動副ZR分別與定平臺上點B1和連桿A1A2上A1點相連接。連接B2與A2的運動鏈結構為ZRZRZRXR，轉動副ZR與定平臺上點B2相連接，轉動副XR與連桿A1A2上A2點相連接，連接B3與A3的運動鏈結構為YRwRPwRYR，轉動副YR與定平臺上點B3相連接，另一個轉動副YR與動平臺A3A4的點A3相連接。動平臺A3A4與連桿A1A2通過平行四邊形四桿機構連接。

3 機構運動模式自由度分析

3.1 3T運動模式

3.1.1自由度分析

如圖5所示，在Bi點建立與坐標系OXYZ對應平行的坐標系oixiyizi。分析圖5所示機構的自由度，第1種方法，以A3A4作為動平臺，先計算運動鏈B1A1，運動鏈B2A2施加在連桿A1A2的約束旋量，然后求解連桿A1A2的運動螺旋，接著得到連桿A1A2連接平行四邊形機構R41R42R43R44后得到的混聯(lián)運動鏈的運動旋量，求解混聯(lián)運動鏈施加在動平臺A3A4上的約束旋量，最后結合運動鏈B3A3施加在動平臺A3A4的約束旋量，對其求解互易積計算動平臺A3A4的自由度。混聯(lián)運動鏈中的驅動副產生的驅動旋量也可以使用上述方法進行計算，這種方法計算量較大。第2種方法，可以將圖5中連桿A1A2作為動平臺，支鏈B1A1作為第1支鏈，支鏈B2A2作為第2支鏈，支鏈B3A3連接平行四邊形機構R41R42R43R44作為第3支鏈，計算圖5所示機構在鎖定驅動副后的自由度。使用這種方法，可將具有混聯(lián)支鏈的機構轉換為并聯(lián)機構，改變了機構動平臺的選取，機構的自由度不會發(fā)生改變，便于支鏈約束旋量、驅動旋量分析，但該方法不能求解動平臺A3A4的運動模式和自由度。因而，使用旋量理論分析機構運動模式時，使用第1種方法。計算鎖定驅動副后機構的自由度，分析驅動副選取合理性時，使用第2種方法。

圖5所示機構轉動副R12的軸線l1和R24的軸線l2異面，轉動副R31的軸線l3與轉動副R35的軸線l4平行。結合圖2a機構所具有的2T1R運動模式，平行四邊形機構R41R42R43R44等效為移動副P。圖5機構位形下，混聯(lián)運動鏈B1A1B2A2-P在定坐標系OXYZ下的約束旋量為

(5)

同理，支鏈B3A3在定標系OXYZ下施加在動平臺A3A4上的約束力偶旋量可表示為

(6)

結合式(5)、(6)可知，動平臺上施加的約束系不存在冗余約束，υ=0，采用修正的Kutzbach-Grübler公式計算機構自由度。值得注意圖5中混聯(lián)支鏈B1A1B2A2-P可等效為ZRZRZRP，因而n、g、fi應參照使用等效支鏈ZRZRZRP替代混聯(lián)運動鏈B1A1B2A2-P后的結構取值。機構自由度為

M=6×(7-7-1)+9+0=3

(7)

機構具有3個自由度，對動平臺A3A4上的約束旋量求解互易積，可知動平臺A3A4在圖5所示位形下，具有3T運動模式，即沿空間的3維移動自由度。根據(jù)文獻[20]的方法判定運動模式是否瞬時，對應每一個自由度和其性質依次給出相對起始位型的一個足夠小的有限位移。可以驗證該3維移動自由度是全周的。

3.1.2驅動副選取合理性分析

當鎖定支鏈中驅動副后機構自由度為零，說明驅動副選取正確。否則說明驅動副選取錯誤。將圖5所示機構，運動鏈B1A1中的移動副P13，運動鏈B2A2轉動副R21，運動鏈B3A3中的移動副P33作為驅動副。圖5所示機構位形下，支鏈施加在連桿A1A2上的約束力旋量為

(8)

鎖定運動鏈B1A1中的移動副P13，運動鏈B2A2轉動副R21(鎖定移動副P33不在連桿A1A2施加驅動力旋量)，施加在連桿A1A2上的驅動力旋量系為

(9)

結合式(8)、(9)組成的旋量系可知，該旋量系中的6個旋量在機構3T運動模式的一般位形下，線性無關，連桿A1A2上施加的約束系不存在冗余約束，υ=0。考慮到圖5中平行四邊形機構R41R42R43R44等效為移動副P，因而n、g、fi應參照使用移動副P等效替代平行四邊形機構R41R42R43R44后的結構取值，則自由度為

M=6×(7-8-1)+12+0=0

(10)

機構具有0個自由度，可知機構在圖5所示機構位形下，選取的3個驅動副能實現(xiàn)機構3T運動模式的控制。

3.2 3T1R瞬時自由度位形

3.2.1自由度分析

當控制3個驅動副使機構從圖5所示位形做3維移動，運動到圖6所示機構位形。圖6所示機構位形下，轉動副R12的軸線l1和R24的軸線l2異面，轉動副R31的軸線l3與轉動副R35的軸線l4平行(不重合)，轉動副R32的軸線l5平行于Z軸，結合圖2a機構所具有的2T1R運動模式，施加在動平臺A3A4上的約束旋量在定坐標系OXYZ中可表示為

(11)

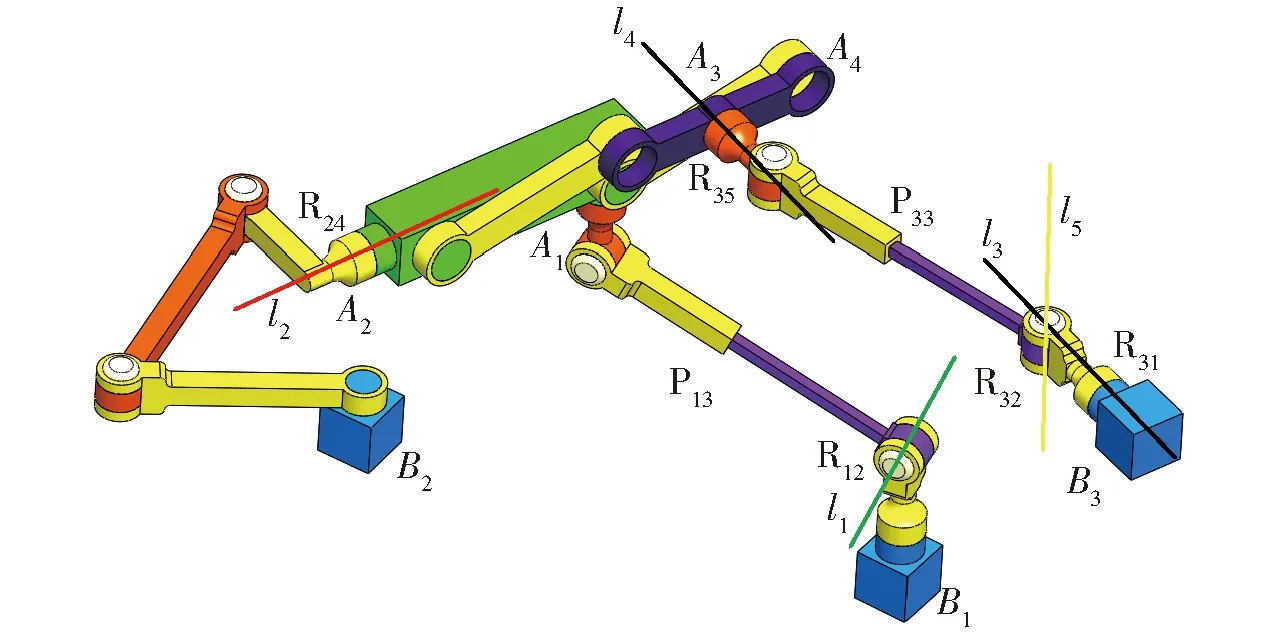
圖6 3T1R瞬時自由度位形Fig.6 3T1R instantaneous DoF configuration

圖6所示機構施加在動平臺A3A4上的約束系存在冗余約束，υ=1。采用修正的Kutzbach-Grübler公式計算機構自由度。考慮到圖6中混聯(lián)支鏈B1A1B2A2-P可等效為ZRZRZRP，因而應參照使用等效支鏈ZRZRZRP替代混聯(lián)支鏈B1A1B2A2-P后的結構對n、g、fi取值，自由度為

M=6×(7-7-1)+9+1=4

(12)

機構具有4個自由度，對動平臺A3A4上的約束旋量求解互易積，可知機構在圖6所示位形下，機構動平臺A3A4具有1個平行于Z軸的轉動自由度和3個移動自由度。考慮到機構從圖5所示位形運動到圖6所示位形，機構自由度由3T變?yōu)?T1R，且機構在圖5所示位形下的自由度是全周的，因而圖6所示機構4個自由度是瞬時的。

3.2.2驅動副選取合理性分析

鎖定運動鏈B1A1中的移動副P13，運動鏈B2A2中的轉動副R21，鎖定運動鏈B3A3中的移動副P33(鎖定移動副P33不在連桿A1A2上施加驅動旋量)，施加在連桿A1A2上的驅動力旋量為

(13)

施加在連桿A1A2上的約束力旋量為

(14)

結合式(13)、(14)組成的旋量系可知，該旋量系中的6個旋量在圖6所示機構位形下，線性相關，υ=1。采用修正的Kutzbach-Grübler公式計算機構自由度。考慮到圖6中平行四邊形機構R41R42R43R44等效為移動副P，因而n、g、fi應參照使用移動副P等效替代平行四邊形機構R41R42R43R44后的結構取值。自由度為

M=6×(7-8-1)+12+1=1

(15)

因而，機構具有1個自由度，可知機構在圖6所示位形下，選取的3個驅動副不能實現(xiàn)機構3T1R瞬時自由度位形下的控制。

3.2.3輔助驅動副選取

根據(jù)3.2.2節(jié)的分析結果，鎖定運動鏈B1A1中的移動副P13，運動鏈B2A2中的轉動副R21，運動鏈B3A3中的移動副P33后，并不能實現(xiàn)對機構在3R1T瞬時自由度位形下的控制。因而，需要增加輔助驅動副。選取輔助驅動副時，應使得輔助驅動副的數(shù)目盡可能少，且輔助驅動副的布置盡可能靠近基座，以減少設備的制造成本和設備的運動慣量。當鎖定輔助驅動副和支鏈的常規(guī)驅動副后，機構的自由度為零，則說明機構的輔助驅動副選取正確。轉動副R11、R31都可作為輔助驅動副的備選選項。選取運動鏈B3A3中的轉動副R31作為輔助驅動副，鎖定該驅動副后，在連桿A1A2施加驅動力旋量

(16)

結合式(13)、(14)、(16)，該旋量系中的7個旋量在圖6所示機構位形下，滿秩且線性相關，υ=1，采用修正Kutzbach-Grübler公式計算機構自由度。圖6中平行四邊形機構R41R42R43R44等效為移動副P，因而n、g、fi應參照使用移動副P等效替代平行四邊形機構R41R42R43R44后的結構取值。自由度為

M=6×(7-8-1)+11+1=0

(17)

根據(jù)式(17)可知，當鎖定運動鏈B1A1中的移動副P13，運動鏈B2A2中的轉動副R21，運動鏈B3A3中的移動副P33和轉動副R31后，機構自由度為零，因而可以通過控制上述驅動副，實現(xiàn)機構在圖6所示3T1R瞬時自由度位形時對機構的控制。可鎖定移動驅動副P13、轉動驅動副R21、輔助轉動驅動副R31后，控制移動驅動副P33即可實現(xiàn)動平臺A3A4繞平行于Z軸的軸線轉動。動平臺A3A4繞平行于Z軸的軸線轉動后，支鏈B3A3中的轉動副R31、R35軸線相交，根據(jù)3.3.1節(jié)的分析可知，此時機構離開3T1R瞬時自由度位形。

3.3 2T1R運動模式

3.3.1自由度分析

當控制圖6所示機構的3個驅動副和1個輔助驅動副，使得機構動平臺A3A4繞平行于Z軸的軸線轉動后，機構處于圖7所示位形，轉動副R12的軸線l1和R24的軸線l2異面，轉動副R31的軸線l3與轉動副R35的軸線l4相交，轉動副R32的軸線l5平行于Z軸。結合圖2a機構所具有的2T1R運動模式，施加在動平臺A3A4上的約束旋量可表示為

(18)

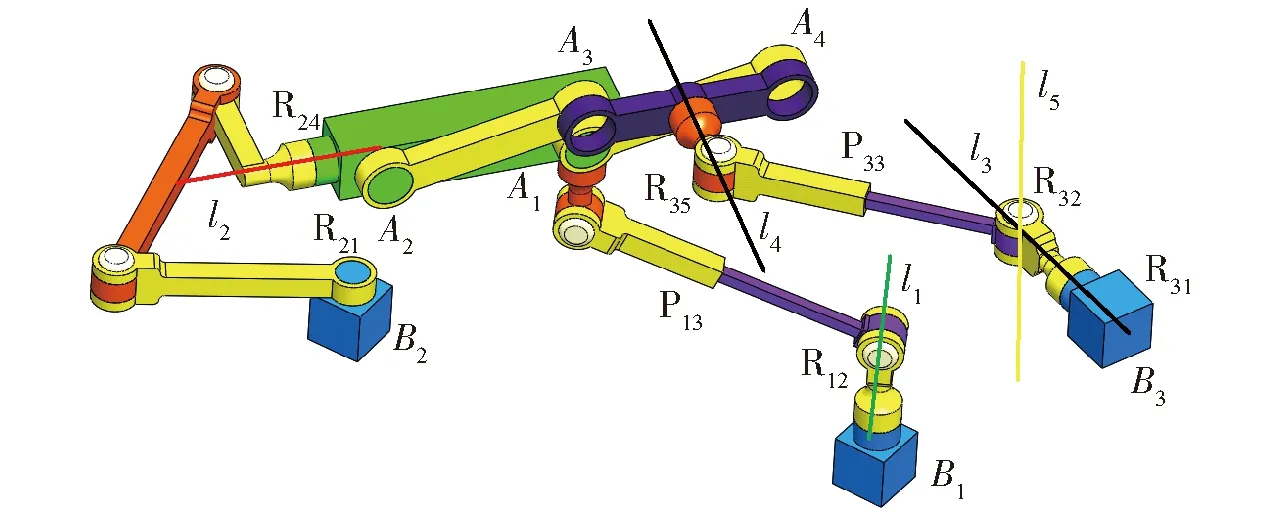
圖7 2T1R運動模式Fig.7 2T1R motion mode

動平臺A3A4上施加的約束系不存在冗余約束，υ=0。采用修正的Kutzbach-Grübler公式計算機構自由度。 考慮到圖7中平行四邊形機構R41R42R43R44等效為移動副P，圖7中混聯(lián)支鏈B1A1B2A2-P可等效為ZRZRZRP，因而應參照使用等效支鏈ZRZRZRP替代混聯(lián)支鏈B1A1B2A2-P后的結構對n、g、fi取值。自由度為

M=6×(7-7-1)+9+0=3

(19)

機構具有3個自由度，結合動平臺A3A4上的約束，對其求解互易積，可知機構動平臺A3A4在圖7所示位形下，具有2T1R運動模式，即沿XOY平面的2個移動自由度和繞平行于Z軸軸線轉動的1個轉動自由度。可以驗證該3自由度是全周的。

3.3.2驅動副選取合理性分析

當機構處于圖7所示位形，鎖定驅動副P13、R21、P33在連桿A1A2上施加驅動力旋量為

(20)

施加在連桿A1A2上的約束力旋量為

(21)

結合式(20)、(21)可知，該旋量系中的6個旋量在機構2T1R運動模式的一般位形下，線性無關，連桿A1A2上施加的約束系不存在冗余約束，υ=0，采用修正的Kutzbach-Grübler公式計算機構自由度。考慮到圖7中平行四邊形機構R41R42R43R44等效為移動副P，因而n、g、fi應參照使用移動副P等效替代平行四邊形機構R41R42R43R44后的結構取值。自由度為

M=6×(7-8-1)+12+0=0

(22)

機構具有0個自由度，可知機構在圖7所示位形下，選取3個驅動副能實現(xiàn)對機構2T1R運動模式的控制。

3.4 2T2R瞬時自由度位形

3.4.1自由度分析

當控制圖7所示機構的3個驅動副，機構從圖7位形繞平行于Z軸的軸線轉動，運動到圖8所示位形，此時轉動副R12的軸線l1與轉動副R24的軸線l2平行，轉動副R31的軸線l3與轉動副R35的軸線l4相交，轉動副R32的軸線l5平行于Z軸。結合圖3b機構具有的2R2T瞬時自由度，施加在動平臺A3A4上的約束旋量為

(23)

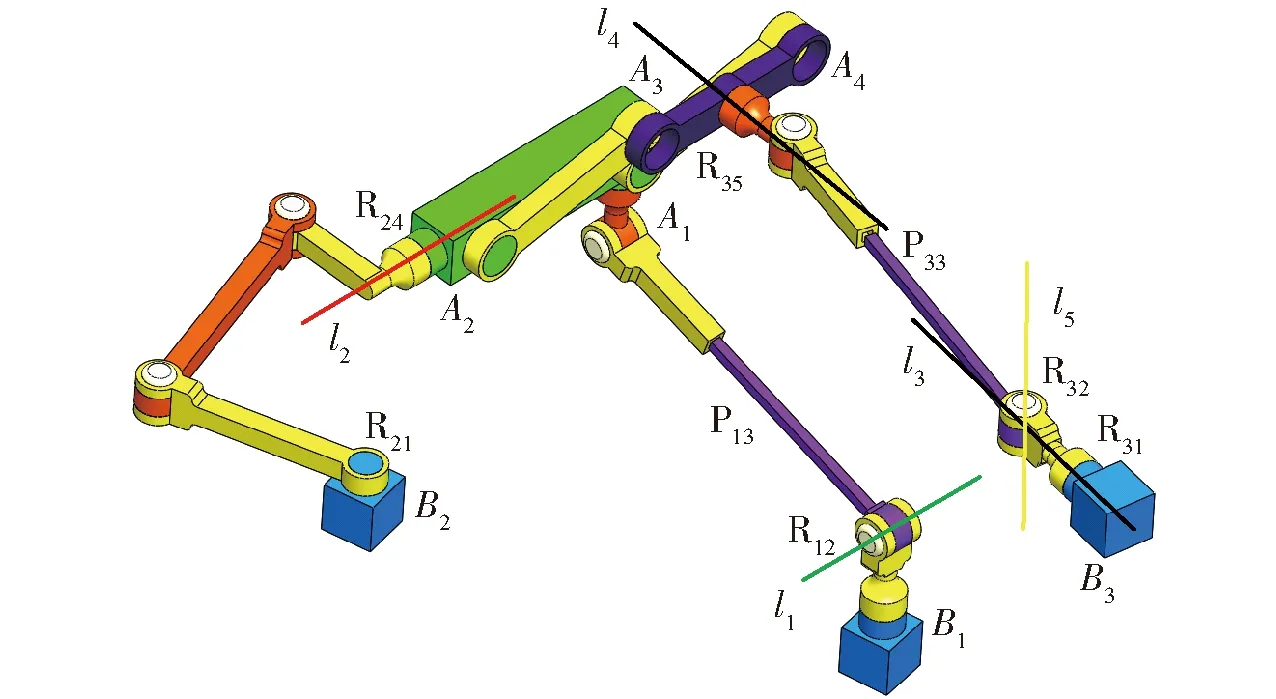
圖8 2R2T瞬時自由度位形Fig.8 2R2T instantaneous DoF configuration

圖8位形下，連桿A1A2具有2R2T瞬時自由度，因而混聯(lián)支鏈B1A1B2A2-P可等效為ZRZRZRvRZP(向量v平行于圖8中軸線l2)，因而n、g、fi應參照使用等效支鏈ZRZRZRvRZP替代混聯(lián)支鏈B1A1B2A2-P后的結構取值。在圖8所示機構位形下，動平臺A3A4上施加的約束系不存在冗余約束，υ=0。采用修正的Kutzbach-Grübler公式計算機構的自由度為

M=6×(8-8-1)+10+0=4

(24)

因而機構具有4個自由度，結合動平臺A3A4上的約束對其求解互易積，可知機構在圖8所示機構位形下，動平臺A3A4具有2個移動自由度和2個轉動自由度。由于圖8所示機構位形是由圖7機構位形繞平行與Z軸的轉軸轉動得到的，且圖7所示位形下動平臺A3A4的3個自由度是全周的，因而圖8位形下動平臺A3A4的2R2T運動模式是瞬時的。

3.4.2驅動副選取合理性分析

圖8所示機構位形下，鎖定移動副P13、轉動副R21、移動副P33，施加在連桿A1A2上的驅動力旋量系為

(25)

施加在連桿A1A2上的約束力旋量為

(26)

結合式(25)、(26)可知，該旋量系中的6個旋量在機構2T2R瞬時自由度位形下，線性相關，動平臺上施加的約束系存在1個冗余約束，υ=1，采用修正的Kutzbach-Grübler公式計算機構自由度。考慮到圖8中平行四邊形機構R41R42R43R44等效為移動副P，因而n、g、fi應參照使用移動副P等效替代平行四邊形機構R41R42R43R44后的結構取值。自由度為

M=6×(7-8-1)+12+1=1

(27)

圖8所示機構具有1個自由度，可知在圖8所示位形下，選取的3個驅動副不能實現(xiàn)機構2R2T瞬時自由度位形下的控制。

3.4.3驅動副選取

根據(jù)3.4.2節(jié)的分析結果，鎖定移動副P13、轉動副R21、移動副P33后，并不能實現(xiàn)對機構在2R2T瞬時自由度位形下的控制。因而，需要增加驅動副，根據(jù)3.2.3節(jié)的內容，選取支鏈3中的轉動副R31作為輔助驅動副，鎖定該驅動副后，在連桿A1A2施加驅動力偶旋量

(28)

結合式(25)、(26)、(28)中的旋量，該旋量系中的7個旋量在機構具有2R2T瞬時自由度時，滿秩且線性相關，υ=1，采用修正的Kutzbach-Grübler公式計算機構自由度。考慮到圖8中平行四邊形機構R41R42R43R44等效為移動副P，因而n、g、fi應參照使用移動副P等效替代平行四邊形機構R41R42R43R44后的結構取值。自由度為

M=6×(7-8-1)+11+1=0

(29)

根據(jù)式(29)可知，當鎖定運動鏈B1A1中的移動副P13、運動鏈B2A2中的轉動副R21、運動鏈B3A3中的移動副P33、運動鏈B3A3中的轉動副R31后，機構的自由度為零，因而可以通過控制上述驅動副，實現(xiàn)機構在2R2T瞬時自由度位形時對機構的控制。可鎖定移動驅動副P13、轉動驅動副R21后，控制移動驅動副P33、轉動驅動副R31，即可使動平臺A3A4產生繞平行于軸線l2的轉動和一維移動。動平臺A3A4繞軸線l2的轉動和做一維移動后，根據(jù)3.5.1節(jié)的分析可知，機構即可離開2R2T瞬時自由度位形。

3.5 2R1T運動模式

3.5.1自由度分析

當控制圖8所示機構的3個驅動副和1個輔助驅動副，機構連桿A1A2從圖8位形繞平行于轉動副R24的軸線l2轉動，運動到圖9所示位形，此時轉動副R12的軸線l1與轉動副R24的軸線l2平行，轉動副R31的軸線l3與轉動副R35的軸線l4相交。結合圖2b機構具有的2R1T運動模式，施加在動平臺A3A4上的約束旋量為

(30)

圖9所示位形下，動平臺上施加的約束系不存在冗余約束，υ=0，采用修正的Kutzbach-Grübler公式計算機構自由度，圖9中混聯(lián)支鏈B1A1B2A2-P可等效為ZRwPvRP(向量v與轉動副R24轉動軸線重合，向量w與移動副P13移動軸線重合)，n、g、fi應參照使用等效支鏈ZRwPvRP替代混聯(lián)支鏈B1A1B2A2-P后的結構取值。自由度為

M=6×(7-7-1)+9+0=3

(31)

機構具有3個自由度，結合動平臺A3A4上的約束對其就求解互易積，可知動平臺A3A4在圖9所示機構位形下，動平臺A3A4具有2個轉動自由度和1個移動自由度，即圖9所示機構位形下，機構具有2R1T運動模式。可以驗證該2R1T運動模式是全周的。

圖9 2R1T運動模式Fig.9 2R1T motion mode

3.5.2驅動副選取合理性分析

圖9所示機構位形下，鎖定移動副P13、轉動副R21、移動副P33，施加在連桿A1A2上的驅動力旋量系為

(32)

施加在連桿A1A2上的約束力旋量為(混聯(lián)變自由度支鏈B3A1A2不在連桿A1A2上施加約束)

(33)

結合式(32)、(33)組成的旋量系可知，該旋量系中的6個旋量在機構圖9所示2R1T運動模式位形下，線性無關，連桿A1A2上施加的約束系不存在冗余約束，υ=0，采用修正的Kutzbach-Grübler公式計算機構自由度。考慮到圖9中平行四邊形機構R41R42R43R44等效為移動副P，因而n、g、fi應參照使用移動副P等效替代平行四邊形機構R41R42R43R44后的結構取值。自由度為

M=6×(7-8-1)+12+0=0

(34)

鎖定圖9中移動副P13、轉動副R21、移動副P33后，機構具有0個自由度，可知機構在圖9所示位形下，選取的3個驅動副能實現(xiàn)機構2R1T運動模式的控制。

綜上所述，該機構使用3個驅動副和1個輔助驅動副，可使得機構從3T運動模式的位形下，運動到3T1R的瞬時自由度位形，變換到2T1R運動模式下，然后運動到2R2T瞬時自由度位形，變換到2R1T運動模式。機構在上述3自由度運動模式下，使用3個驅動副可以實現(xiàn)機構的控制，當機構處于運動模式變換的瞬時4自由度位形時，除了使用3個驅動副以外，還需使用1個輔助驅動副來實現(xiàn)機構運動模式的變換。

4 結論

(1)使用混聯(lián)變自由度支鏈可以實現(xiàn)機構運動模式的變換，提出的一類機構具有3T、2T1R和2R1T運動模式，在不同運動模式的機構位形下，采用旋量理論對機構自由度進行分析，驗證了機構的多模式運動特性。

(2)選取的3個驅動副能在機構3種運動模式的一般位形下，實現(xiàn)對機構的控制，當機構在運動模式變換位形下，具有3T1R或2R2T瞬時自由度時，需要增加1個輔助驅動副，控制該輔助驅動副和上述機構的3個驅動副可以實現(xiàn)機構運動模式的變換。