熵值法對某礦用自卸車駕駛室振動的分析與優化

周新濤,崔亞輝,馬 娜

(西安理工大學 機械與精密儀器工程學院,陜西 西安 710048)

礦用自卸車在路況條件非常復雜的礦區工作,如路面凸凹不平、石塊障礙物多、多彎和多坡道等情況,其運行條件極其惡劣[1-2].車輛在運行過程中,當外激勵的振動頻率與懸置系統的固有頻率相接近時,將會產生共振,從而使駕駛室的駕乘舒適性大幅度降低[3].駕乘人員若長時間置身于振動幅度較大的環境中,極易疲勞,進而影響到車輛駕駛的安全性[4].因此,近年來車企、學者等對礦用車輛駕駛室駕乘舒適性問題都十分關注.

當前,為了解決礦用自卸車駕駛室懸置系統隔振性差的問題,通常情況下廣泛采用被動隔振的方式來改善駕駛室駕乘的舒適性.如采用理論模擬仿真的方式來分析駕駛室系統的振動情況,然后根據分析結果來指導減振系統的改進[5-6].該方法在實際使用過程中,對某些礦用車輛駕駛室振動系統的改進有一定的指導意義.但車輛在礦區行駛的環境復雜多變,理論仿真與實際運行情況差距較大,故該方法難以從根本上解決駕駛室振動問題.另外一種途徑是采用實際測試法,根據礦用自卸車的實際運行工況,真實地測量出各懸置系統的振動特征信號.之后,對實測振動信號進行深入分析,找出影響礦用自卸車駕駛室舒適性差的根本原因,進而指導駕駛室減振系統的改進[7-9].在復雜多變的環境中進行試驗測試,所獲得的信號將會被周圍的干擾信號嚴重污染,若只按照傳統方法對被測信號進行處理,不能完全消除干擾信號,有用的信號會被削弱,導致后續對車輛駕駛室懸置系統優化后的減振效果不明顯或優化失敗等結果.

本文將會在上述研究的基礎上，采用有效的方法,對礦用自卸車駕駛室懸置系統的振動特性進行研究.首先,通過實測試驗得出礦用自卸車駕駛室各懸置系統的振動信號,采用多尺度排列熵(Multiscale Permutation Entropy,MPE)法對獲得的被測信號進行深入處理,消除干擾信號從而保證被測信號的純度;然后,通過對有效信號的頻譜分析和振動能量傳遞路徑分析找出問題,優化駕駛室懸置系統相關的減振特性參數,使駕駛室的駕乘舒適性達到最佳狀態.

1 振動特征分析理論

先簡單介紹MPE的計算原理和分析方法,為后續對礦用自卸車駕駛室懸置系統振動實測信號的預處理及懸置振動特征提取作為理論支撐.

1.1 奇異值分解理論

奇異值分解[10](Singular Value Decomposition,SVD)的實質是將實測信號進行正交變換,對信號中的高頻隨機噪聲有很好的過濾效果.SVD法所得到的矩陣奇異值具有唯一性、穩定性和比例不變性等性質,其變換關系式為

(1)

式中:U和V為變換后的正交矩陣;S為奇異值矩陣.

1.2 排列熵算法理論

排列熵(Permutation Entropy,PE)法是由Bandt等[11]提出,常用于定量描述一維時間序列復雜程度的非線性指標,具有計算簡單、抗噪聲能力強、分析時所需時間序列短等優點.PE法的計算關系為

(2)

式中:m為時間序列的嵌入維數;τ為延遲時間;T(ω)為任意一種排列方式ω出現的相對頻次;N為原始時間序列的尺度.

由式(2)可以得出,序列復雜程度越低,排列熵值越小;反之,排列熵值就越大.PE法能用序列排列方式的變化放大信號中的細微波動,從而反映信號中的異常情況.

1.3 MPE法理論

MPE法的概念是由Aziz等[12]在多尺度算法的基礎上提出來的,也是后續采用多尺度算法和排列熵算法相結合的產物.MPE法的計算本質,是將原始時間序列按順序粗粒化的一種處理方式,從而構建出一個新的時間序列,其操作過程如表1所示.

表1 多尺度時間序列粗粒化處理原理Tab.1 Principle of coarse granulation of multi-scale time series

由表1所示的計算原理,對一組原始時間序列進行粗粒化處理,可得出新構建的時間序列的平均值計算關系式為

(3)

式中:λ為尺度因子.

2 道路測試及結果分析

2.1 實車測試

根據礦區用戶反饋,該礦用自卸車在某路面某車速下,駕駛室本體振動幅度過大,嚴重影響到駕駛室的駕乘舒適性.為此,需要對該車進行實測摸底試驗,但在礦用自卸車行業的相關領域中,對該類車輛的道路試驗時測試軟件常采用的是C級隨機路面激勵，而礦區實際的路面情況與軟件所采用的路面激勵有較大差距,從而對后續駕駛室懸置系統的振動分析有很大影響.因此,本文在道路試驗時,根據非公路礦用車運行的實際情況和標準[13-14],選用礦用自卸車常用實際工況下測試的振動數據分析,故本次分析結果更具有實際指導意義.本次測試選用的場地如圖1所示.

圖1 礦區試驗場地Fig.1 The mine test site

本次道路試驗所采用的主要設備為LMS振動數據采集與分析儀,以及多軸向振動加速度傳感器.試驗工況[15]為:礦車滿載100 t,測試車速10,20,30和40 km/h 4種常用車速.測點分別布置在板簧、車架、駕駛室懸置、駕駛室地面(腳墊)和座椅支撐面(座墊)等位置處.在每個工況下分別進行2次測試,以確保測試后獲得的信號正常有效.

2.2 測試數據的MPE法分析

由于在環境復雜的礦區試驗,所測得的試驗信號已受到多種干擾信號的影響,如路面隨機信號、發動機輸出的高頻信號、傳動系統產生的振動信號和其他結構體產生的噪聲等,嚴重影響到振動分析信號的純度.同時,在整個時間序列上,這些振動信號之間的振動特征存在復雜的多尺度耦合現象,使得對駕駛室本體振動特征提取及分析的難度大大增加.本文采用MPE法,能去除信號中的干擾因素,反映出系統振動真實的本質.

2.2.1測試數據的SVD法降噪處理

本次測試布置的測點較多,其座椅座墊處、腳墊處的測點直接與人的身體接觸,此處的振動情況將直接影響到駕乘的舒適性.本節以礦用車最常用的速度20 km/h情況下，座椅座墊處的振動情況為例.如圖2所示座椅處的振動情況,其各方向處的振動加速度數據與其他形式的振動信號高度耦合,從而將座椅處振動特征的本質給淹沒了.故對此測點處的振動特征分析前,先將測試信號進行必要的降噪處理.

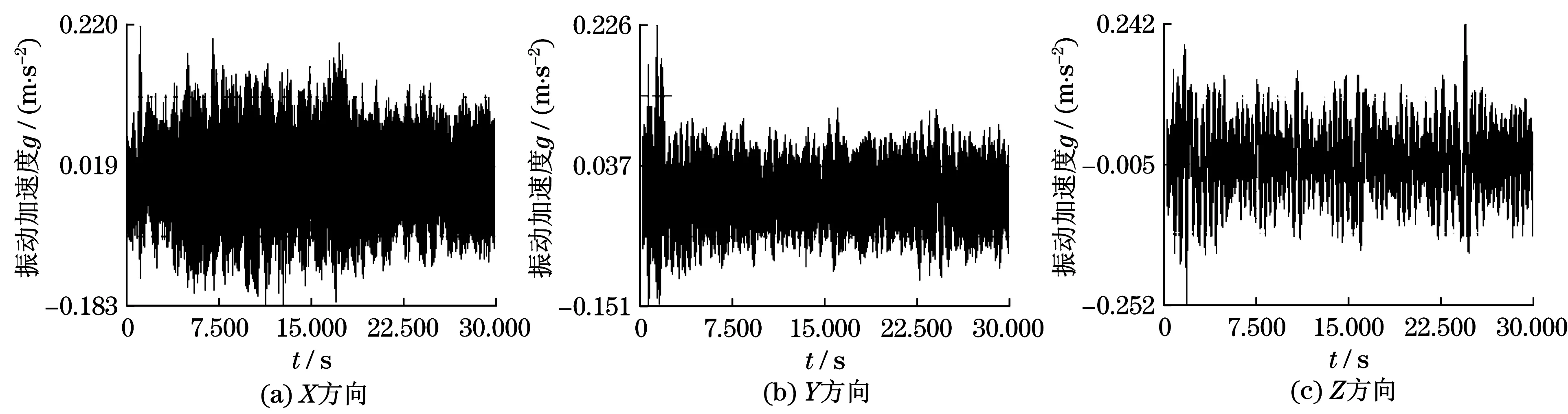
圖2 20 km/h時座椅處實測振動加速度時域圖Fig.2 The time-domain graph of vibration acceleration at 20 km/h

依據SVD原理,將本次所測得的振動信號進行降噪處理.過濾掉噪聲等干擾信號后,利用SVD的逆運算重構振動相空間矩陣,該矩陣就是降噪后振動信號的最佳逼近矩陣.

如圖3所示,通過對測試信號進行SVD后,得出在4種車速下座椅處振動的奇異值,以此判斷噪聲信號所在的相空間.從圖3中可以得出座椅處在X,Y,Z方向的奇異值分布情況大致相同,從一個最大值處大幅度下降,當奇異值為2.15以后其值逐漸趨于0.說明奇異值為2.15處是有效信號和噪聲信號的過渡處,將保留有效信號,并將噪聲信號的奇異值全部置成0以達到降噪目的.

根據信號降噪的原理,SVD降噪的關鍵為找出奇異值的峰值,因此，選擇峰值前的R個奇異值對振動信號進行重構.為了準確地描述奇異值序列的變化規律,需將奇異值序列進行差分譜的計算,找出奇異值差分譜序列的最大值.該值所對應的維數就是振動信號重構的階數.再經過多次試算與調整,確定了各類參數值,得出了座椅處在X,Y,Z方向上奇異值差分譜的變化規律,如圖4所示.由此,可以準確得出振動信號重構的階數.

圖3 座椅處振動信號奇異值的分布圖Fig.3 Distribution graph of singular value of vibration signal in seat

圖4 座椅處振動信號奇異值差分譜的分布圖Fig.4 The distribution graph of differential spectrum of singular value for vibration signal in seat

將被測振動信號經SVD后,剔除噪聲等干擾信號.再通過奇異值差分譜分析,確定了振動信號重構階數,并按該階數將信號重構，為后續的振動分析作基礎.降噪后重構的信號如圖5所示.

2.2.2振動數據的MPE法分析

將降噪后的信號進行MPE分析,得出座椅處X,Y,Z方向上的熵值分布情況.隨著尺度增加,熵值也在不斷增大.說明座椅處的振動情況,隨著尺度因子的增大而惡化,該處的振動情況越復雜,振動源的激勵形式也呈多樣化.如圖6所示:當車速在30 km/h以下時,X方向處熵值變化的規律大致相同;當車速在40 km/h時,X方向處熵值的變化幅度最小,波動較為平穩.Y方向處熵值,受車速變化情況的影響程度最大.Z方向上熵值的波動規律與X方向處的基本相同.

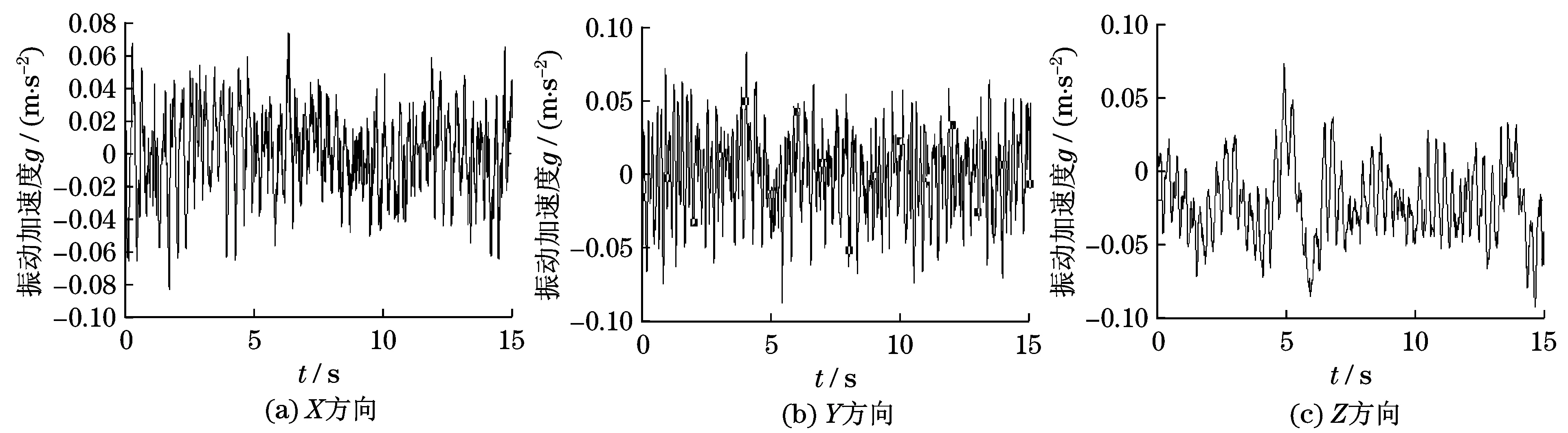
圖5 20 km/h時座椅處經SVD降噪后的振動加速度時域圖Fig.5 The SVD de-noised for the time-domain graph of vibration acceleration in seat at 20 km/h

圖6 座椅處經SVD降噪后的MPE特征關系圖Fig.6 The MPE feature graph of seat after SVD noise reduction

3 座椅坐墊處的頻響分析

在駕駛室與駕乘人員振動響應系統中,主要考慮駕乘人員對振動最敏感的頻段[16].人體最敏感頻率為:垂直方向的頻率為4 Hz,前后方向的頻率為0.629 5 Hz,左右方向的頻率為0.652 Hz.根據文獻和標準中給出的權值,將這3個方向上頻率加權后得出0～20 Hz范圍.當人體暴露在這些頻段附近時,即使暴露的時間較短,也會感覺到十分不適.而當頻率在0.5 Hz以下的低頻高振幅的環境中,將會對人體產生較大的機械損傷,如扭傷、碰傷等情況.

如圖7所示:當車速在10 km/h、20 km/h時,座椅處X,Y,Z方向的頻率均在0～20 Hz的范圍內,且座椅處水平方向的振動比垂直方向的復雜很多;當車速在30 km/h時,座椅處水平方向的振動能量較小,垂直方向的振動能量較大(即上下顛簸幅度較大);當車速在40 km/h時,座椅處水平振動頻率增大,Z方向的振動頻率較小.對座椅3個坐標方向上的振動頻率分析,得出的振動響應與上述振動熵值分析的結果相近.

4 駕駛室懸置系統優化

通過上節頻響分析,得出座椅處的振頻剛好落在0～20 Hz范圍內,導致駕駛室駕乘平順性較差,故需要對該車駕駛室懸置系統的減振性能進行優化.由于駕駛室及其他部件的布置位置較為緊湊,懸置系統的安裝區域較小,若重新設計懸置系統的結構,此法就難以實現,并且受周期長、成本增加等因素的制約.因此,本文在優化懸置系統的減振性能時,主要從懸置支撐剛度和阻尼參數匹配兩方面入手.

按照特定的設計準則多次調整匹配和試算驗證,得出駕駛室懸置系統的一組較為理想剛度和阻尼參數.根據這組參數重新裝配好懸置系統,再按上述相同的方法與條件進行實測,得出駕駛室座椅處的振動響應情況,如圖8所示.通過對圖7與圖8對比分析,得出優化后的懸置系統的峰值頻率范圍,整體向后推移到22～45 Hz內,能有效地避開人體對振動最敏感的頻段.

圖7 座椅處經SVD降噪后的頻響特性關系圖Fig.7 Relationship graph of frequency response characteristics of seat after SVD noise reduction

圖8 座椅處經SVD降噪優化后的頻響特性關系圖Fig.8 The graph of optimization frequency response characteristics of the seat after SVD noise reduction

5 結論

本文根據礦用自卸車工作時,駕駛室振動幅度較大的問題,采用試驗測試法優化其懸置系統的減振特性.通過本研究得出如下幾點結論:① 依據礦用自卸車的工作工況和相關標準,對該車駕駛室的振動情況進行了摸底試驗,得出了駕駛室座椅處的振動特性;② 采用SVD將被測振動信號進行了奇異值和奇異值差分譜計算,根據其計算結果重構出無噪聲及干擾的真實特征信號(即信號的降噪處理);③ 將降噪后座椅處的信號進行MPE分析,得出該處X,Y,Z方向上的熵值分布情況;④ 在上述基礎上,對座椅處在不同車速下的振動情況進行頻響分析,得出該處的頻響特性剛好處在人體敏感的區間范圍內;⑤ 結合該車駕駛室懸置系統的實際安裝情況,對懸置系統的減振性進行優化,優化后懸置系統的減振效果較好.