考慮彈性連接的結構振動環境預示方法

楊艷

攀枝花學院交通與汽車工程學院,四川 攀枝花617000

飛行器在發射、飛行過程中將經受復雜且嚴酷的振動環境，為了保證飛行器的高可靠性，必須通過地面振動環境試驗。合理地制定振動環境條件，對飛行器的研制至關重要。過低的環境條件將導致欠試驗，使飛行器在地面試驗中無法充分暴露潛在缺陷，飛行器在實際環境下發射、飛行可能失敗；過高的環境條件將導致過試驗，使飛行器必須通過高于實際環境的地面試驗，從而導致飛行器研制難度的增加，進而造成研制周期過長、經費浪費等[1,2]。當有大量的實測環境數據時，基于統計歸納方法所制定的環境條件與實際環境最為接近。但對于新研飛行器而言，存在較多的不確定參數，且實測環境數據匱乏，故而導致制定環境條件本身的需要與飛行器研制對環境條件的需求往往是矛盾的。在這種情況下，準確高效的振動環境預示則是解決問題的必然選擇[3]。

然而，飛行器是一個十分復雜的結構系統，復雜結構中往往存在著大量的彈性連接（例如螺栓連接），彈性連接對結構振動特性的影響不可忽視[4]。因此，合理地等效彈性連接是準確進行結構振動環境預示的一個重要前提。文獻[5,6]利用六自由度標量彈簧-阻尼系統等效結構中的彈性連接，對考慮彈性連接的結構振動環境預示方法進行了初步研究，并取得了一定的研究成果，但這種等效方法沒有考慮彈性連接各自由度間的耦合作用，與工程實際并不相符。文獻[7]通過大量的計算、比對，并結合相關的有限元理論知識，由數值結果反推出BUSH 單元的剛度矩陣，發現BUSH 單元單個結點的剛度矩陣并非對角陣，存在垂向移和轉角的耦合剛度項，可更為準確地等效工程實際結構中的彈性連接。鑒于此，BUSH 單元也在航天領域結構建模中得到了廣泛應用。但是，直接利用傳統的FEM 對飛行器的振動環境進行預示時，若要提高預示精度，則需對飛行器的結構進行精細化建模，這會導致計算成本驟增，故需開發更為高效的結構振動環境預示方法。文獻[8,9]指出，FIMSM為高效處理復雜結構動力學特性問題的方法，故利用FIMSM 對考慮彈性連接的結構振動環境進行準確高效地預示具有切實的可行性。

綜上所述，本研究利用MSC.Nastran 軟件中的BUSH 單元等效復雜結構中的彈性連接，基于FIMSM 對考慮彈性連接的結構固有頻率進行了理論推導，并通過算例仿真驗證了該方法的正確性。本研究所得結論具有一定的理論研究和工程應用價值。

1 BUSH 單元剛度矩陣

文獻[7]基于數值結果反推的研究思路，首先，利用DMAP 語言輸出BUSH 單元的剛度矩陣；然后，改變輸入參數并記錄剛度矩陣的變化規律；最后，通過分析大量的計算結果獲取BUSH 單元剛度矩陣Kb的解析表達式。剛度矩陣Kb按2 個結點進行分塊，如下所示：

上式中，4 個分塊矩陣K11、K12、K21和K22的解析表達式分別如下所示：

式中：ki（i=1,2,…,6）為BUSH 單元的6 個輸入參數；L為單元長度。通過查閱文獻[10]可知，BUSH 單元與剪切梁單元的剛度矩陣形式相同，都存在垂向位移和轉角的耦合剛度項，故與六自由度標量彈簧-阻尼系統相比，BUSH 單元可更為準確地等效工程實際結構中的彈性連接。

2 考慮彈性連接的結構固有頻率

如圖1 所示，設整體結構是由P和Q兩部分組成，且P和Q之間通過n個規格相同的彈性連接（pi～qi，i=1,2,…,n）進行連接。

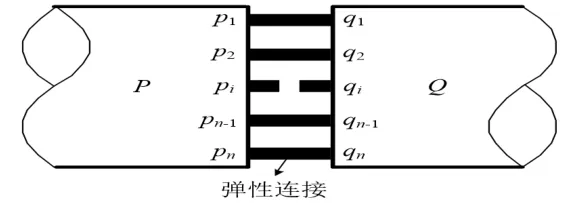
圖1 整體結構示意圖Fig.1 Schematic chart of overall structure

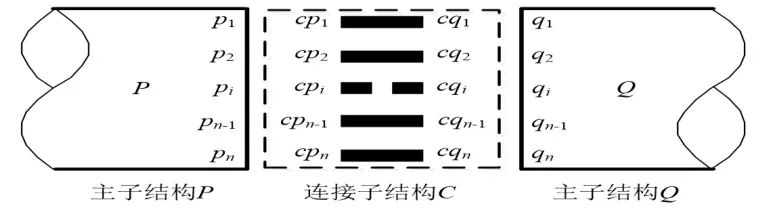
圖2 子結構劃分示意圖Fig.2 Schematic chart of substructure partition

為了提高計算效率，本研究利用FIMSM 對圖1 所示考慮彈性連接的結構固有頻率進行計算。FIMSM 的基本步驟為[11]：1）根據結構特點和分析要求，將整體結構劃分成若干固定界面的子結構；2）基于FEM 提取各子結構的模態信息，計算各子結構參加模態綜合的假設模態集，即低階保留主模態和約束模態；3）根據界面位移協調條件，利用各子結構的假設模態集進行模態綜合，建立整體結構自由度縮減后的振動方程，并進一步開展計算分析。

對于圖1 所示的整體結構，若忽略彈性連接的影響，可將其劃分成P和Q兩個子結構進行處理，則對應的界面結點集Pv和Qv分別為：

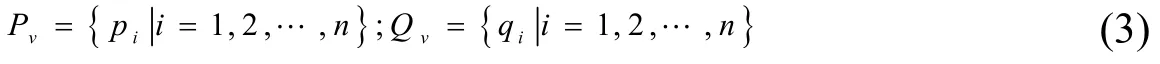
文獻[11]指出，相鄰子結構間的界面位移協調是FIMSM 所要求的。然而對于圖1 所示的子結構P和子結構Q而言，由于二者之間為彈性連接，故Pv和Qv中對應界面結點的位移并不連續，若直接利用FIMSM 計算其固有頻率，則會產生一定的誤差甚至錯誤。此時，若將子結構P和子結構Q之間的彈性連接單獨劃分成一個只有界面結點的連接子結構C，則不僅能夠滿足子結構的劃分原則，還可通過連接子結構C將子結構P和子結構Q的界面位移協調起來。因此，本研究將圖1 所示的整體結構劃分成P、Q和C3 個獨立的子結構進行處理，如圖2 所示。

待子結構劃分完成后，首先基于FEM 提取主子結構λ（λ=P,Q）的物理參數，即質量矩陣Mλ和剛度矩陣Kλ；然后按照內部結點u和界面結點v將主子結構λ的質量矩陣Mλ和剛度矩陣Mλ進行分塊整理，如下所示：

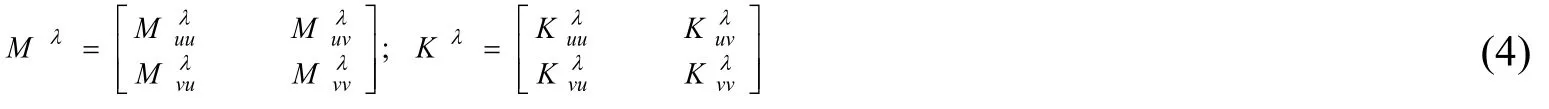
此時，根據子結構主模態和約束模態的定義，可得主子結構λ的主模態和約束模態的計算公式分別為[11]：

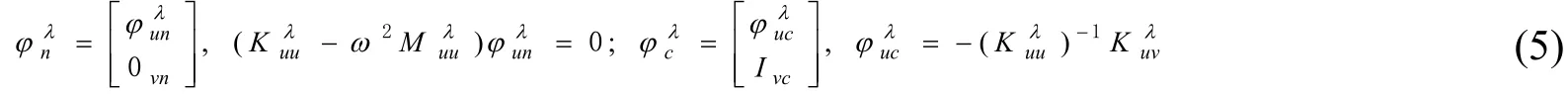
式中：ω為角頻率；I為單位矩陣。假設選取前r（r＜＜n，從而實現自由度的縮減及計算效率的提高）階主模態作為子結構λ的低階保留主模態，則子結構λ參加模態綜合的假設模態集φλ可寫為：

對于圖1 所示的彈性連接而言，由于其質量很小，對整體結構振動特性的影響可忽略不計[8,9,12]。對于彈性連接的剛度而言，本研究采用BUSH 單元對其進行等效。因此，連接子結構C的質量矩陣MC和剛度矩陣KC可分別寫為：

同理，根據式(5)，可得連接子結構C參加模態綜合的假設模態集φC為：

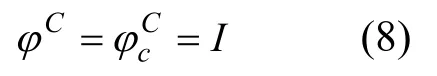
式中：φC c為連接子結構C的約束模態。待獲得各子結構的質量矩陣、剛度矩陣以及參加模態綜合的假設模態集后，可將整體結構的質量矩陣M、剛度矩陣K和模態矩陣φ分別寫為：

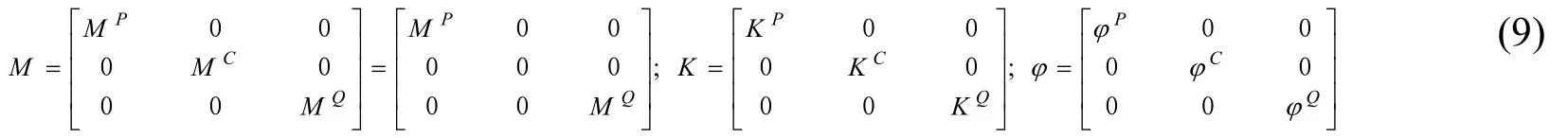
設整體結構的位移列向量為X，則有：

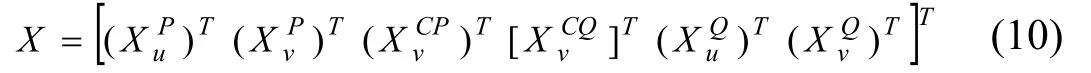
式中：Xλ u和Xλ v分別為主子結構λ的內部結點和界面結點位移列向量；XCλ v為連接子結構C與主子結構λ對應的界面結點位移列向量。記整體結構模態矩陣φ的模態坐標為Y，則有：

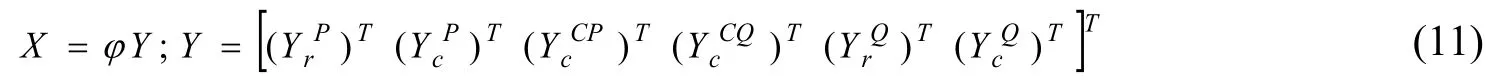
引入界面位移協調條件為：

式中：LP和LQ為坐標旋轉變換矩陣。對式(10)～(12)以及式(13)進行整理可得：

引入獨立變換矩陣S對Y進行獨立變換，變換過程如下所示：

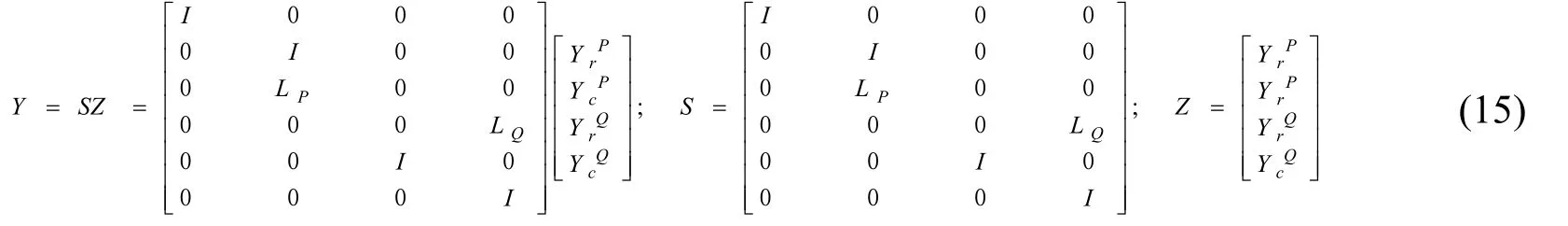
式中：Z即為整體結構獨立的模態坐標。此時，則可得整體結構對應于獨立模態坐標Z的模態質量矩陣MZ和模態剛度矩陣KZ分別為：

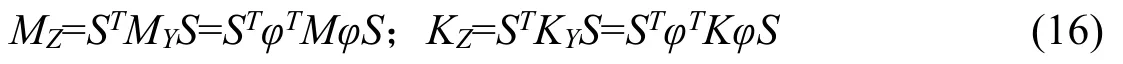
因此，基于FIMSM 建立的圖1 所示整體結構自由度縮減后的無阻尼自由振動方程為：

記式(17)所示振動方程的模態矩陣為Φ，則其計算公式和表達式分別為：

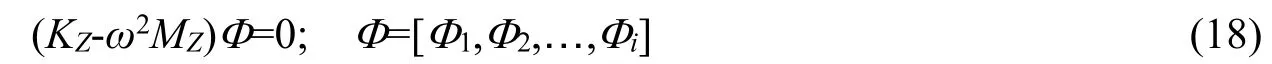
此時，由瑞利商公式可得圖1 所示整體結構的第i階角頻率ωi為：

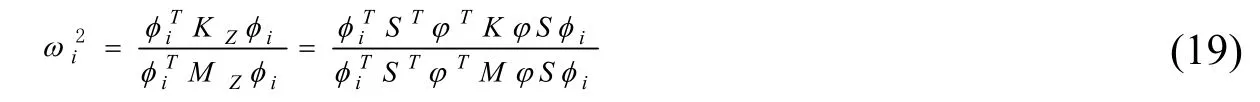
上述過程即為利用BUSH 單元等效結構中的彈性連接，并基于FIMSM 推導所得考慮彈性連接的結構固有頻率表達。由于FIMSM 未考慮各主子結構高階主模態的影響，故可大幅提升計算效率。

3 算例驗證

為了驗證上述方法的正確性，設計了一個如圖3 所示具有彈性連接的算例結構，在利用BUSH單元等效彈性連接的前提條件下，分別利用FIMSM 和FEM 對該結構的前30 階固有頻率進行計算，并對計算結果進行對比。

圖3 中，P、Q和R為三根相同的矩形截面長梁，截面尺寸和梁長度分別為0.04 m×0.02 m 和0.5 m，利用剪切梁單元對其進行單元劃分，單元屬性參見表1；C為2 個完全相同的彈性連接，利用BUSH 單元來等效，單元屬性參見表2。

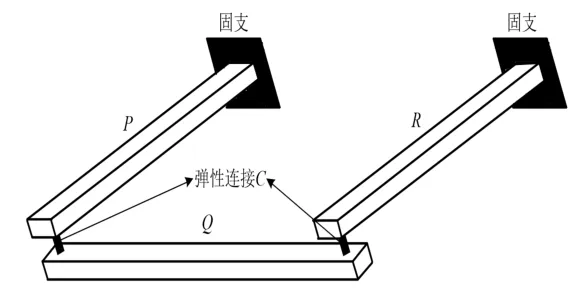
圖3 算例結構示意圖Fig.3 Schemaric structure of the diffset

表1 剪切梁單元屬性Table 1 Element attributes of the shear beam

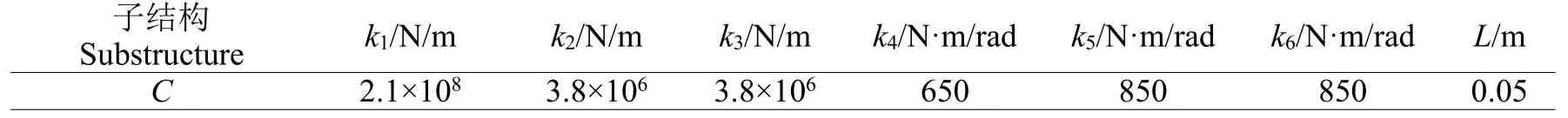
表2 BUSH 單元屬性Table 2 Element attributes of BUSH

在利用FIMSM 計算時，分別保留主子結構P、Q和R的前10 階作為低階保留主模態參加模態綜合；而在利用FEM 進行計算時，選用的則是整體結構的全部模態。兩種方法的計算結果見表3。

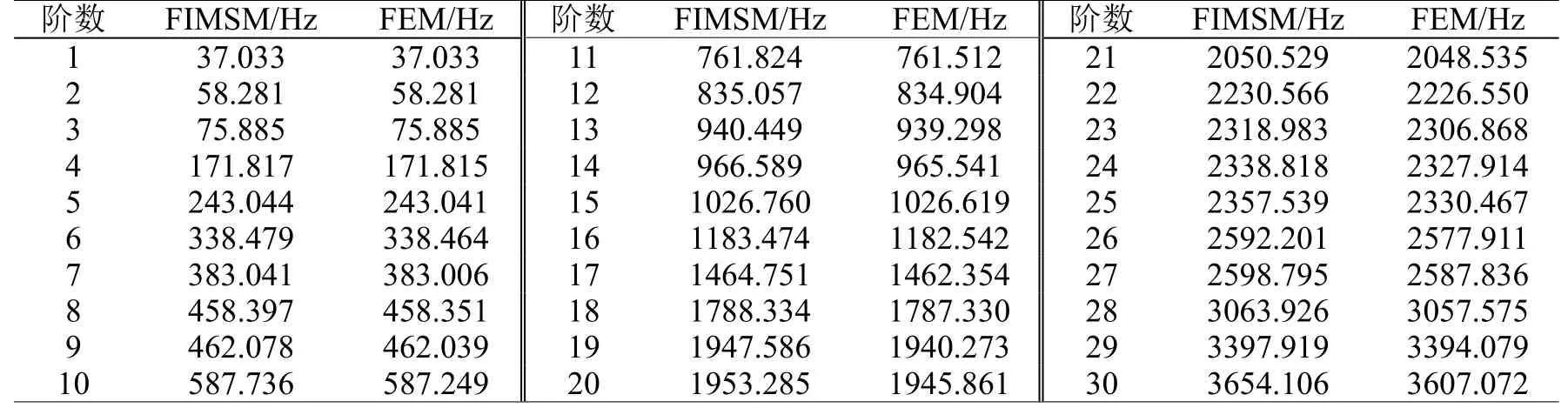
表3 固有頻率計算結果Table 3 Calculating results from intrinsic frequencies

由表3 可知，與傳統的FEM 相比，FIMSM 對圖3 所示算例結構前30 階固有頻率的相對計算誤差不超過±1.31%。綜上所述，利用BUSH 單元等效彈性連接，FIMSM 可對考慮彈性連接的結構固有頻率進行準確高效地計算。

4 結論

本研究利用MSC.Nastran 軟件中的BUSH 單元等效彈性連接，基于FIMSM 對考慮彈性連接的結構固有頻率進行了理論推導，并通過算例仿真對該方法的正確性進行了驗證。結果表明：利用BUSH 單元等效彈性連接，FIMSM 可對具有彈性連接結構的振動環境進行準確高效地預示。本研究所得結論具有一定的理論研究和工程應用價值。