大型民機系統縱向Nz控制律設計

張翰 謝殿煌

摘 要：針對國內民機系統縱向穩定性較差、飛機縱向短周期模態響應穩定性不足等問題，以某大型民機為研究對象，基于特征結構配置方法，利用逆模型的思路確定控制系統前饋增益系數，并基于某典型配平狀態點，利用線性模型設計該飛機縱向控制律。線性仿真分析中，利用俯仰角速率q響應準則評價控制方案效果。仿真結果表明，采用特征結構配置方法設計的縱向飛行控制律具有良好控制效果，可以改善系統飛行品質使其達到一級飛行品質要求，相比于經典控制理論，通過特征結構配置方法進行縱向Nz控制律設計可以一次性確定反饋增益系數，縮短控制律設計時間。

關鍵詞：民機飛控系統;縱向控制律;特征結構配置;線性仿真分析;飛行品質

DOI：10. 11907/rjdk. 201261????????????????????????????????????????????????????????????????? 開放科學（資源服務）標識碼（OSID）：

中圖分類號：TP319 ? 文獻標識碼：A ??????????????? 文章編號：1672-7800（2020）011-0150-04

Longitudinal Nz Control Law Design for the Large Civil Aircraft System

ZHANG Han，XIE Dian-huang

（State Key Laboratory of Civil Aircraft Flight Simulation， Commercial Aircraft Corporation of China， Shanghai 201210， China）

Abstract： Aiming at the problems of poor longitudinal stability of domestic civil aircraft system and insufficient longitudinal short period modal response stability of aircraft， this paper takes a large civil aircraft as the research object， studies the method based on characteristic structure configuration， and uses the idea of inverse model to determine the feedforward gain coefficient of control system. Besides， based on a typical trim state point， the longitudinal control law of the aircraft is designed by using the linear model. Through the linear simulation analysis， the quality effect of the control scheme is evaluated by using the pitch rate q response criterion. The simulation results show that the longitudinal flight control law designed by eigenstructure configuration method has good control effect and can improve the flight quality of the system to meet the requirements of the first level flight quality. Especially， compared with the traditional control theory， the feedback gain coefficient can be determined once and the design time of the control law can be shortened.

Key Words：civil aircraft flight control system; longitudinal control law; eigenstructure configuration; linear simulation analysis; flight quality

0 引言

隨著現代民用飛機飛行包線不斷擴大，特別是國內某些干線航線緊張，民機逐步向高空高速發展。飛行控制律作為飛機的“靈魂”，直接影響飛機安全性和舒適性[1-2]。飛行控制系統設計是我國大型客機研制過程中的關鍵技術之一，對于提高飛機性能、飛行安全以及減輕駕駛員工作負荷至關重要[3-4]。

王永[5]分析了我國民機飛控系統研制與西方國家的差距，提出我國大型客機研發需要在增強可靠性與安全性、提高適航取證能力、降低成本、發展多層次系統化的飛控產品等方面有所突破。面對與日俱增的市場需求，加上日趨明顯的歐美技術封鎖，研制出具有自主知識產權的大型客機飛行控制系統刻不容緩[6-9]。日前，中國商飛正充分爭取全球資源，集全國之力發展大型客機項目，本文來源于民機飛行控制律設計相關項目，對我國大型客機研制具有一定參考意義。

1 研究對象

本文以某大型民機為研究對象，利用經典方程描述飛機的動力學和運動學模型，選取12個狀態變量，其它變量通過這12個變量導出求得。選取典型巡航狀態的配平點，在配平點附近通過小擾動線性化方法得到線性模型。縱向控制律基于線性模型而設計。本體模型架構如圖1所示。

2 特征結構配置方法

特征結構配置方法在民機飛行控制系統中應用十分廣泛，特征根可以改善系統響應的動態特性，特征向量可以對系統進行動態響應解耦，通常綜合配置特征根和特征向量使系統達到預期響應[11-14]。一般地，線性時不變系統的狀態方程如下：

x=Ax+Buy=Cx

其中，A∈Rn×n，B∈Rn×m，C∈Rp×n，n為飛機狀態變量個數，p為觀測輸出個數，m為系統輸入個數。

特征結構配置可以概述為：針對給定的自共軛標量集{λdi}和對應的自共軛n維向量集{vdi}，確定一個m×n維實數矩陣K，使得A+BK的特征值與共軛標量集{λdi}一致，其對應的特征向量與n維向量集{vdi}一致。

基于狀態反饋的控制原理結構如圖2所示，反饋增益矩陣K中各元素的正負需要根據反饋信號的極性確定，計算時以u=Kx加以處理。

基于Moore的研究表明，若系統可控，則特征向量需滿足以下3個條件：

當且僅當對于每個i有：①{vdi}ni=1為復域Cn中的一組相互獨立的特征向量;②當λi=λ*i時，vi=v*i;③vi∈span{Nλi}。

可求得反饋矩陣的增益矩陣為：K=-Mλ1z1 -Mλizi ？ -Mλnznv1 vi ？ vn-1，當rank（B）=m時，反饋矩陣K存在且唯一[10]。

3 縱向NzU控制律設計

3.1 Nz控制律

Nz控制屬于閉環控制，可以提高操縱指令性和飛機穩定性，使姿態控制更加精準，具有中性速度穩定性，指駕駛桿處于中立位置時，在飛行速度改變情況下，通過縱向控制律的積分模塊自動配平飛機，最終達到平飛過載，極大地減輕了飛行員的負擔，同時提高了飛行員的舒適性[15-16]。

Nz控制律和國外部分機型采用的C*控制律均具有中性速度穩定性，C*信號是俯仰角速率和法相過載信號的綜合，飛機在低速飛行狀態下，俯仰角速率變化幅度較大，飛行員主要按照飛機的俯仰角速率進行操縱;而在高速飛行狀態下，飛機法相過載變化幅度較大，飛行員主要按照法相過載對飛機進行操控[17]。C*信號表示如式（1）所示。

C*=nz+Vcog·q? ? ? （1）

Nz控制律和C*控制律均可以實現對飛機縱向姿態的精準控制，由于國內關于C*控制的研究文獻相對較少，可供參考的型號經驗有限，而目前Nz控制律已經初步在民機領域上得到了應用，因此選用Nz控制律進行設計。

3.2 配平與線性化

基于搭建好的六自由度非線性模型，利用MATLAB自帶的Trim函數和Linmod函數進行線性化及配平，依據某典型配平狀態點確定飛機系統在該配平點附近的線性化狀態矩陣為：

Alon=-0.96-0.001 9401-8.801-0.019 6-9.8100001-2.6617.0e-05 -3.57e-15-0.476，Blon=-0.023 6-0.004 20.61154.00300-1.0420.053 1

系統的特征根、阻尼比以及固有頻率等自然特性如表1所示。

其中，狀態變量選取了迎角α、飛行速度V、俯仰角θ和俯仰角速率q，x=α，V，θ，qT;控制輸入為升降舵偏度和油門桿開度，u=δe， δTT。

3.3 縱向Nz控制架構

考慮到僅采用C*增穩控制其評價效果與飛行員評估之間相關性不強，控制效果不理想，且常規飛行控制系統中不能同時兼顧飛行穩定性和操縱性，通過設計Nz控制增穩系統可以同時兼顧以上兩個方面[18-21]。縱向控制增穩結構如圖3所示。

該控制框圖主要包括4個控制模塊：指令模型、反饋模型、執行機構和飛機本體模型。

3.4 前饋通道及參數配置

前饋通道從飛行員桿力指令輸入出發，分成3部分：其中一條前饋通道直接乘上增益Kff，傳給作動器，驅動舵面偏轉，這會使飛機具有快的響應速度;另外兩條前饋通道經由指令模型（通常可以采用適合的二階系統模型），形成法相過載指令nzcmd和法相過載變化率指令nzcmd，然后分別乘以前饋增益Kd和Kp，與第一條前饋通道相加共同組成升降舵前饋指令信號，相比于常規直接由駕駛桿指令到舵面作動器，可以提高飛行品質。

3.4.1 指令模型

指令模型是控制系統架構中前饋通道的重要組成部分，可以看作是一個前置濾波器，指令模型能夠為系統提供合適的指令信號。本文研究的控制架構是將飛行員的桿力操縱指令轉化為法相過載指令和法相過載變化率指令，從而使系統更好地響應飛行員操縱指令，滿足操縱品質的要求，可以進一步擴大飛機的飛行包線[22-23]。本文研究的指令模型形式如式（2）所示。

nz_cmdδstk=ω2cmds2+2ζcmds+ω2cmd? ? ? ? ?（2）

其中，zcmd取值1.0，可以使系統具有良好的阻尼特性，ωcmd=ωsp，可以使系統具有良好的短周期頻率特性，也可以保證升降舵作動器作動平穩，本文指令模型如式（3）所示。

nz_cmdδstk=3.098 3s2+3.520 4s+3.098 3 （3）

通常而言，短周期頻率是在不同的配平狀態點進行配置得到。由圖3控制框圖可以看出，通過指令模型輸出的法相過載指令nzcmd和法相過載變化率指令nzcmd通過前饋系數Kd和Kp傳輸給升降舵作動器。此外，桿力指令通過前饋參數Kff，輸入到升降舵作動器，驅動升降舵舵面偏轉。其中，從飛行員桿力指令輸入到指令模型的前饋增益Kstick取值為1/50 lb/g（磅每牛頓）。

3.4.2 前饋參數

前饋參數有Kd、Kp和Kff，與常規求解或定義前饋參數的方法不同，本文通過定義一個等效的低階二階逆模型，進行前饋參數反求解。等效逆模型定義的二階傳遞函數如式（4）所示。

nzδele=Kinve-τinvss2+2ζinvωinvs+ω2inv? ? ? （4）

巡航狀態下配平點附近的法相過載響應經過解耦簡化處理后的傳遞函數如式（5）所示。

Δnz（s）Δδe（s）=-0.229 s - 10.238s2+1.436s+3.118? ? ?（5）

通過逆模型各項參數和指令模型各項參數，可以確定3個前饋增益系數如式（6）所示。

kp=（ω2inv-ω2cmd）/kinvω2invkd=（2ζinvωinv-2ζcmdωcmd）/kinvω2invkff=ω2cmd/kinvω2inv? ? ? ? ? （6）

控制系統在該配平點附近的短周期法相過載響應伯德圖如圖4所示，為頻率范圍從0.1rad/s到1.5倍的飛機短周期模態響應頻率。

3.5 反饋通道及參數配置

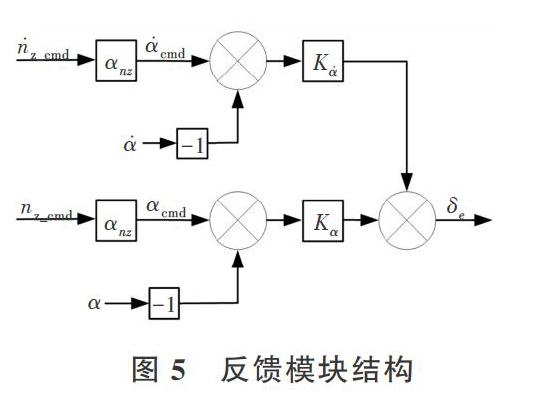
反饋通道可以改善系統的阻尼特性和短周期頻率，反饋信號采用飛機法相過載反饋nz，但實際上nz是根據迎角信號αz轉化得到的，nz反饋可以提高飛機系統本身的靜穩定性，同時也能滿足系統對于阻尼特性和短周期頻率的要求。其中，控制系統反饋模塊如圖5所示。

其中，αnz是在短周期運動模態中，迎角和法相過載之間的轉換系數，具體表達式如式（7）所示。

αnz=αn=VgZα? ? （7）

迎角速率信號α可以通過飛機的俯仰角速率q經過一定轉換得到，具體表達式如式（8）所示。

α=q+gcos？cosθcosα+sinθsinα-nzU? ? ? ?（8）

對于巡航平穩飛行狀態，俯仰角θ與迎角α相等，且法相過載nz為1，因此迎角速率α等于俯仰角速率q。

通過αnz可以將法相過載指令nz和法相過載變化率指令nz轉化為迎角指令信號α和α，然后與飛機本體的迎角反饋和迎角變化率反饋信號作差，再乘以適當的反饋增益系數Kα和Kα，對這兩條反饋通路求和，共同組成了反饋信號指令，這也是常規意義下的比例—積分（PI）控制環節。

反饋通道的反饋增益K可以采用特征根結構配置方法求得。系統短周期運動模態特征根為-0.722 9±1.604 9i，阻尼比為0.410 7。由GJB185-86一級標準規定，最小無阻尼自振頻率不小于1.0，阻尼比不小于0.19。Nz控制律設計主要針對飛機的短周期運動模態而言，選擇短周期運動特征根為-0.8±0.8i，阻尼比選擇為0.707。

則期望的特征值如式（9）所示。

λd=-0.8+0.8i -0.8-0.8i * *? ? ?（9）

狀態反饋的控制律u = -Kx+v，具有期望特征值的閉環系統特征多項式為：

f（λ*）=（λ*+0.8-0.8i）（λ*+0.8+0.8i）

取K=kα，kα，則設計的閉環系統特征多項式為：f（λ）=|λI-A+BK|，然后由f（λ*）=|f（λ）|，通過求解該方程即可得到反饋增益矩陣K=-1.762 6，0.197 4，*，*，該增益矩陣可以保證閉環系統的特征值為期望值。

3.6 仿真驗證分析

基于上述方法得到控制律，利用MATLAB的Simulink在配平點附近搭建線性數學模型，并進行線性仿真分析。在單位方波輸入下，模型輸出如圖6所示。可以看出在Nz控制架構下，飛機法相加速度響應效果良好，且超調量較小，當飛行員撤銷駕駛桿指令輸入時，飛機也能很快進入穩態。

將在該平衡點附近設計的控制律應用于非線性六自由度模型，觀察飛機在該平衡點附近的響應，并通過俯仰角速律q響應準則評價控制方案的品質效果，巡航飛行速度為100m/s，飛機俯仰角速率響應曲線如圖7所示。

根據圖7俯仰角速率q在Nz控制器下的單位階躍輸出曲線，結合俯仰角速率響應準則，檢驗控制器效果。

（1）有效延遲時間t1≈0.05，可以滿足1級飛行品質要求。

1級：t1≤ 0.12 s;2級：t1≤ 0.17 s;3級：t1≤ 0.21。

（2）瞬態峰值比（Δq2/Δq1）max≤0.1，可以滿足1級飛行品質要求。

1級：（Δq2/Δq1）max≤0.3;2級：（Δq2/Δq1）max≤0.6;3級：（Δq2/Δq1）max≤0.915。

（3）有效上升時間Δt≈ 0.2，同樣滿足終端飛行階段1級飛行品質要求。

級別? ? ? ? ?非終端飛行? ? ?終端飛行? ? ? ? ?1級 9/V0≤Δt≤500/V0? ? ? ? 9/V0≤Δt≤200/V0? ? ? ? 2級 3.2/V0≤Δt≤1 600/V0 3.2/V0≤Δt≤645/V0

式中，V0為真空速（m/s），配平點巡航飛行速度為100m/s。

綜上所述，設計的Nz控制器可以滿足俯仰角速率準則1級飛行品質要求，設計的Nz控制器可以滿足設計指標，達到預期效果。

4 結語

以上研究表明，采用特征結構配置法設計的縱向飛行控制律具有良好控制效果，響應平滑迅速，可以達到俯仰角速率1級飛行品質要求。此外，通過特征結構配置方法可以一次性求得所需反饋增益系數，縮短了控制律設計時間，提高了效率。但是存在的問題是，采用特征結構配置方法進行控制律設計時，無法預測未配置極點的最終狀態，因此可能變得非常不穩定，或者某些閉環極點阻尼太小。這種情況下，需要改變特征值重新設計，從而達到預期目標。通常情況下，大多數理想的閉環極點與開環極點差異不大，因此未配置的極點穩定性也不會造成很大問題。

參考文獻：

[1] 朱妍，景海峰，高亞奎. 空客飛機電傳控制律設計分析[C]. 深圳：中國航空學會2007年學術年會，2007.

[2] 邵榮士. YF-16電傳操縱系統控制律分析[J]. 飛機設計，1998，19（4）：26-34.

[3] 姚子羽. 大型商用民航飛機振動故障控制律研究與設計[J]. 系統仿真學報，2015，27（2）：295-302.

[4] 吳勝亮. 民用飛機控制律設計與飛行品質評估試驗方案研究[J]. 軟件導刊，2017，16（8）：160-163.

[5] 王永. 民機飛控系統的發展思路研究[J]. 系統仿真學報，2009，20（S2）：200-204.

[6] 杜金剛. 基于動態逆方法的飛行控制系統設計與仿真[D]. 西安：西北工業大學，2006.

[7] 謝陵. 民用飛機控制律設計系統工程過程研究[J]. 軟件導刊，2015，14（5）：41-43.

[8] 李欣. 大型客機自動飛行控制律研究[D]. 南京：南京航空航天大學，2013.

[9] 周蜜.? A320飛機電傳操縱系統的控制律及其重構淺析[J]. 科技風，2016，29（12）：12-13.

[10] ANON.Flight control design-best practice[R]. NATO RTO-TR-029，2000.

[11] PRATT R W. Flight control system[J]. AIAA Progress in Astronautics and Aeronautics，2000（184）：375-382.

[12] ANON.Flying qualities of piloted aircraft[S].? MIL-STD-1797B， Department of Defense Interface Standard，2006.

[13] TISCHLERY M B，TOM BERGER.Longitudinal control law design and handling qualities optimization for a business jet flight control system[Z]. 2014.

[14] 楊玉蕾. 民機自動飛行系統工作模式研究[D]. 南京：南京航空航天大學，2012.

[15] 姬猛. 推力不對稱時民機飛行控制律重構技術研究[D].? 南京：南京航空航天大學，2011.

[16] 周立冬. 無人直升機前飛狀態飛行控制律設計技術研究[D]. 南京：南京航空航天大學，2011.

[17] 李樂堯，李儼，王新民. 放寬靜穩定性大型客機縱向控制增穩系統設計[J]. 飛行力學，2010，28（4）：25-28.

[18] 張平，張明峰，陳宗基. 民機電傳飛控系統適航安全舒適性要求初探[J]. 系統仿真學報，2008，20（S2）：216-219，228.

[19] 王美仙，李明，張子軍. 飛行器控制律設計方法發展綜述[J]. 飛行力學，2007，25（2）：1-4.

[20] 歐陽紹修，劉振欽. 大型運輸機橫航向飛行品質要求探討[J]. 飛行力學，2007，25（1）：12-14.

[21] 王會，李紹燕，陳宗基. 基于μ綜合方法的運輸機縱向自動著陸控制律[J]. 北京航空航天大學學報，2003，48（12）：1059-1063.

[22] 周其煥. 民用飛機自動飛行控制系統的發展（上）[J]. 航空電子技術，2001，32（4）：43-47.

[23] 楊一棟，牛佩翼，江浩. 飛行控制系統模態轉換瞬變抑制技術的研究[J]. 航空學報，1990，26（1）：88-92.

（責任編輯：孫 娟）