基于失效—停機時間的公共汽車二級保養效果
莫旭冕,蔣仁言,陳志高
(1.長沙理工大學汽車與機械工程學院,湖南長沙 410114;2.長沙理工大學數學與統計學院,湖南長沙 410114)
0 引言
公共汽車的許多零部件隨時間退化,最終會使系統失效。預防維修常常被實施來減緩這個過程以延長系統壽命。預防維修的優劣將直接影響系統的工作狀態。許多企業將其設備維護業務進行外包。因此,預防維修效果建模受到維修管理人員的廣泛關注。已經有許多學者對其進行了研究,這些研究大致可以分為三類:一類是失效強度減少模型;另一類是虛擬年齡減少模型;最后一類是其他評估模型。有很多文獻從失效強度減少這一角度來建立維修模型[1-3]。同樣,也有很多文獻從虛擬年齡減少這一角度來建立維修模型[1-2,4-5]。還有很多文獻從其他角度來建立維修模型[6-10]。然而,文獻[1-7]中所提到的模型的計算相對較復雜,文獻[10]中模型則需要在特定的維修政策下才能應用。文獻[8]是對文獻[9]的一個擴展,通過對比保養前后的失效強度來評價保養效果。用泊松過程模型來描述可修系統的失效過程,而泊松過程模型又用平均累積函數(Mean Cumulative Function,MCF)來描述。并引進了加權的思想,用權函數來反映不同時間失效數據的重要性。
文獻[8]的權函數關于預防維修時間對稱,但是預防維修之前的經驗MCF 與預防維修之后的經驗MCF 相差較大,直接用相近的權值對相差較大的MCF 進行加權不合理。
在本研究中,將預防維修之前的經驗MCF 進行變換,使之與預防維修之后的經驗MCF 相差不大,消除二者之間的隱含加權,期望得到更為穩健的評價結果。另外,還用該方法對失效停機時間進行建模來評價保養效果,發現失效停機時間同樣可以用來建模評價保養效果,并且所提出的轉換在用失效停機時間進行建模時的優勢更加突出。
1 用加權最小二乘法評價預防維修效果
1.1 基本假設
基本假設有兩個:一是忽略修理時間,失效過程被簡化為失效點過程;二是失效點過程用冪律模型來近似描述。冪律模型為M(t)=(t/η)β。其中,η 為尺度參數,β 為形狀參數。令α=1/ηβ。
1.2 基本思想
基本思想是可修系統的可靠性常用失效發生率來描述。失效發生率是系統在單位時間內的平均失效次數,即平均累積函數的微分,并記為M(t)。冪律模型的失效發生率為M(t)=(β/η)β(t/η)β-1。
假設在時間τi執行了一次預防維修(如汽車的二級保養),在τi之前和之后的失效發生率分別為:

其中,Δt 可取為車輛維修的質保期。
令Δm 表示預防維修前后變化的失效發生率,即Δm=mi(τi)-mi+1(τi)。越大,表示預防維修的效果越好。也可以用相對值Δm/mi(τi)評價預防維修的效果。具體情況可以參考文獻[8]。
1.3 加權最小二乘法
最小二乘法通過最小化誤差的平方和來進行曲線擬合,它認為所有的點的誤差同等重要。而在某些情況下,只需要在某些點的附近取得較好的擬合效果。為此,Jiang[11]提出了加權最小二乘法。加權最小二乘法通過最小化以下加權的平方誤差和來獲得參數。

要在某些確定的點左右兩側一定范圍內擬合較好,即這個范圍內的權重相對較大。權函數如下:

其中,φ(.)是正態分布的概率密度函數,它的均值為μ,標準差為σ。
在正態分布的概率密度函數中,t=μ 附近的值較大,所以取μ=τi。σ 的值通過式(3)來確定。

2 改進的建模過程
由于加權最小二乘法對靠近預防維修的失效點更重視,然而預防維修點左鄰域的經驗MCF 和預防維修點右鄰域的經驗MCF 相差較大,因而直接對其進行加權不合理(圖1)。為此,對預防維修點左鄰域的經驗MCF 進行變換。變換的要求:①變換后的經驗MCF 和右鄰域的經驗MCF 相差很小;②變換后左鄰域的經驗MCF 的斜率的絕對值不變。以下變換符合以上要求。

圖1 預防維修前后的經驗MCF
令預防維修之前經驗MCF 的最大值為a,最小值為b,變換之前的經驗MCF 記為y,變換之后的經驗MCF 記為y1,則y1=a+b-y。變換結果如圖2 所示。

圖2 預防維修之前經驗MCF 的變換
下面來看具體的改進建模步驟。
步驟1:數據預處理。原始數據為失效日期,需將失效日期轉換為失效時間。
步驟2:計算(τi-1,τi)內的經驗MCF,將系統在(τi-1,τi)內的失效時間從小到大排序,并記為{tk,1≤k≤N}。令M(t)表示一個系統在[0,t]內失效次數的期望值,即M(t)=E[N(t)]。顯然,。
這里s(tk)為在tk時仍在運行的系統數目。由上式可知,平均累積函數在tk時刻存在跳躍,為保持其平滑性,定義其經驗平均累積函數為。
步驟3:將步驟2 得到的經驗MCF 進行本小節開始所述的變換。
步驟4:計算(τi,τi+1)內的經驗MCF,計算方法與步驟2 一樣。
步驟5:計算(τi-1,τi)和(τi,τi+1)內失效數據的權重值,靠近τi的數據點包含更多該點的失效強度信息,應該賦予較大的權重值,遠離τi的數據點應賦予較小的權重值。失效數據的權重值用方程式(2)來確定。
步驟6:用加權最小二乘法擬合(τi-1,τi)內的失效數據到下列冪律模型,即Mi(t)=αi(τi-t)βi。
步驟7:用加權最小二乘法擬合(τi,τi+1)內的失效數據到下列冪律模型,即Mi+1(t)=αi+1(t-τi)βi+1。
根據Δm=mi(τi)-mi+1(τi)計算Δm,其中Δt 的取值可依據參考文獻[12],二級維護質量保證期為車輛行駛5000 km 或30 d,因此取Δt=30 d。
改進的步驟有步驟3、步驟6 和步驟8。文獻[8]沒有進行步驟3 所述變換,直接用加權最小二乘法擬合(τi-1,τi)內的失效數據到如下冪律模型:Mi(t)=αitβi。
3 基于失效—停機時間用加權最小二乘法評價預防維修效果
停機時間是反映系統可靠性的重要指標之一,文獻[13]對停機時間進行了建模分析。失效—停機時間不僅反映了停機的次數還傳達了失效的嚴重程度,所以用失效—停機時間來建模可以更準確地反映維修效果。由于每一次失效的停機時間是隨機的,因此對停機時間進行累加處理。具體建模步驟如下。
步驟1:數據預處理。原始數據為失效日期,需將失效日期轉換為失效時間。同時,將失效所需修理時間和保養所需時間提取出來。某車的二級保養時間、失效時間和維修工時數據如表1所示。其中,*為保養時間。

表1 某車的失效時間和維修工時
步驟2:計算(τi-1,τi)內的累積停機時間D(t)。如圖3 所示
步驟3:將步驟2 得到的累積停機時間D(t)進行第2 節“改進的建模過程”中所述變換。
步驟4:計算(τi,τi+1)內的累積停機時間D(t),計算方法和步驟2 相同。
步驟5:計算(τi-1,τi)和(τi,τi+1)內失效數據的權重值。計算方法與2 節的步驟5 一樣。
接下來的步驟同第2 節的步驟6、步驟7、步驟8 和步驟9一樣。
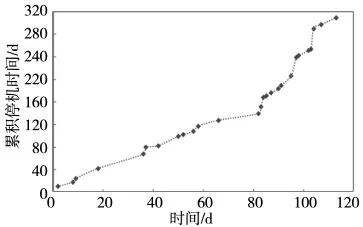
圖3 保養之前的累積停機時間
4 數值實例
以長沙某公交公司的維修保養記錄來詳細說明整個建模過程。收集了由8 輛同型號車組成的車隊的維修保養記錄。收集這些車輛從2007 年1 月1 日到2007 年12 月31 日的維修記錄,提取車輛在二級保養前后的失效時間(累積運行天數)和保養時間的信息及失效和保養所需維修工時。
基于失效時間來評價維修質量,表2 給出了原建模過程的結果,表3 給出了改進建模過程的結果。

表2 基于失效時間用加權最小二乘法評價的維修效果Ⅰ

表3 基于失效時間用加權最小二乘法評價的維修效果Ⅱ
表2 和表3 分別給出了用兩種建模過程的結果,兩種建模過程所得結果基本一致,說明了改進建模過程的有效性。對兩種建模過程的結果進行分析,發現改進建模過程所得維修質量的變異系數(Coefficient of Variation,CV)值較小,即改進建模過程更為穩健。
基于失效—停機時間來評價維修質量,表4 給出了原建模過程的結果,表5 給出了改進建模過程的結果。
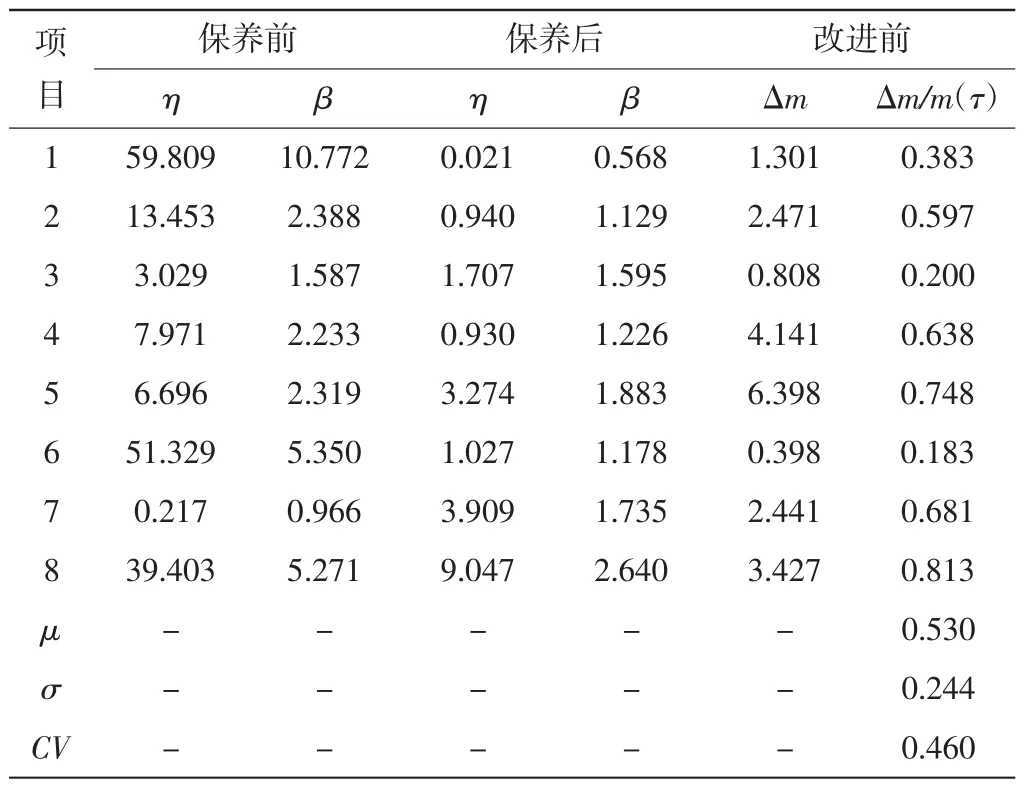
表4 基于失效—停機時間用加權最小二乘法評價的維修效果Ⅰ
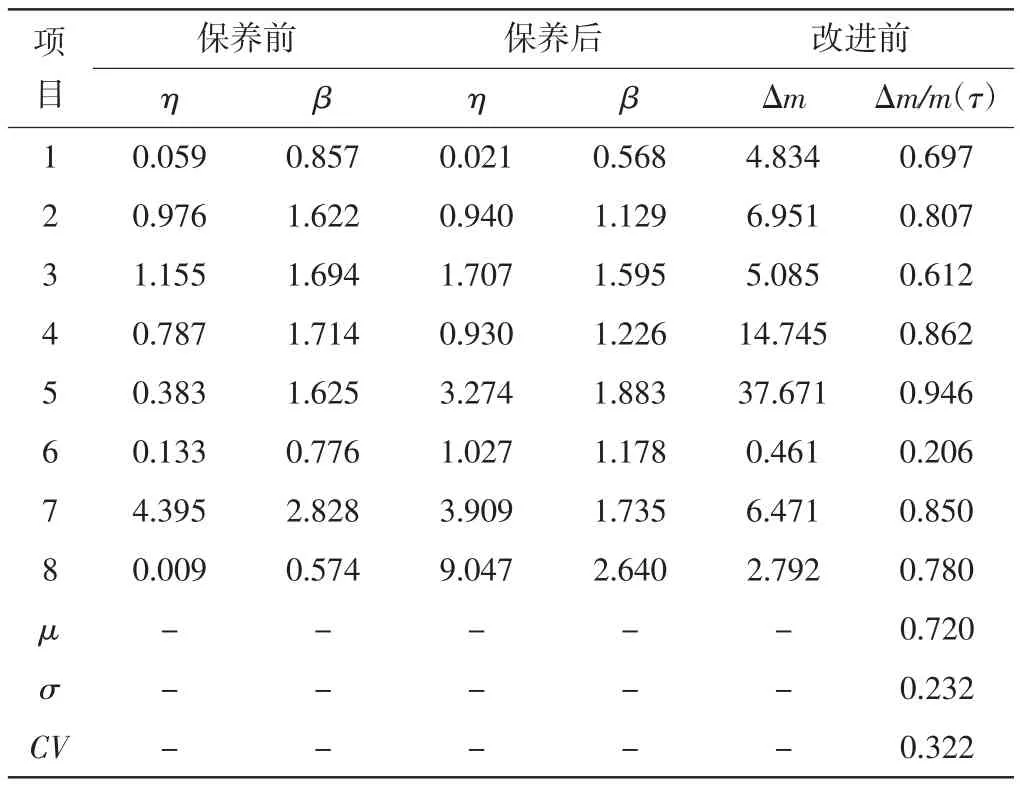
表5 基于失效—停機時間用加權最小二乘法評價的維修效果Ⅱ
由表4、表5 可以看出,兩種建模過程的結果基本一致,且用改進建模過程的結果的CV 值遠小于原建模過程的。可見,改進建模過程更適合基于失效—停機時間建模評價維修質量。對比基于失效—停機時間和失效時間來評價維修質量的結果,可以看出基于失效—停機時間和失效時間進行評價的結果非常接近。因此,基于失效—停機時間來評價維修質量也是可行的。
5 結論
研究了公共汽車二級保養效果評價這一問題,對評價公共汽車二級保養維修質量的加權最小二乘法的建模過程進行了改進;并基于停機時間用改進的建模過程來建模評價二級保養效果。通過一個實例的計算和分析,得出以下結論。
(1)改進建模過程的加權最小二乘法所得結果的CV 值分別比原來小16.8%和30%,即改進建模過程的加權最小二乘法更為穩健。
(2)用原建模過程和改進建模過程對失效—停機時間進行了建模分析,所得結果與基于失效時間建模所得結果基本一致,說明失效—停機時間同樣可以用來建模評價保養效果。
(3)公共汽車二級保養質量波動較大,最好的維修效果和最差的相差74%。為此,加強維修質量控制和選擇合適的維修外包商尤為重要。
(4)基于先前的工作,一方面可以考慮將基于失效時間和基于失效—停機時間兩種數據所得的結果進行折衷處理,另一方面,將維修質量應用于維修質量控制、維修質量管理、維修外包商選擇等領域也值得進一步研究。

