中長期降雨預報模型比較研究

王藝晗 樊孔明

（1.河海大學水文水資源學院 南京 210000 2.加州大學洛杉磯分校土木與環境學院3.淮河水利委員會水文局（信息中心） 蚌埠 233001）

中長期徑流預報成果是月、年調度計劃編制的重要基礎，運用典型年、時間序列分析、遙相關等多種徑流預報模型方法對關鍵水文斷面、水利工程的來水過程進行滾動預報，為流域可供水量分析、水資源調度計劃制定提供數據支撐。

該研究以史灌河流域主要站點的1956～2016年系列水文資料為基礎，采用常見的中長期預報模型，包括AR（AutoRegression）、KNN（k-nearest Neighbor）、BPNN（Back-Propagation Neural Network） 及LSTM（Long-Short term memory neural network）共四種方法進行中長期來水預測。以前期徑流量、前期降雨量作為預報因子輸入，對重點流域的各計算分區進行年、月尺度的中長期來水預報。

根據《流域水資源調度方案編制技術指導（草案）》要求，考慮到BMA（Bayesian Model Averaging）模型在水文水資源領域的廣泛應用，且能夠提供確定性、概率預報兩類預報結果，能提供未來有多大的可能性出現各種等級的降水，該模型研發過程中采用BMA 模型作為多模型集合預報的核心算法，用于綜合AR、KNN、BPNN、LSTM四類模型的預報結果。

1 方法介紹

1.1 AR 模型

AR 模型是最常見的平穩時間序列模型之一，是統計上一種處理時間序列的方法，用同一變量xt的歷史數值，即xt-1至xt-p來預測xt，并假設它們為一線性關系。自回歸模型被廣泛運用在經濟學、信息學、自然現象的預測上。一個p 階自回歸模型可以表示如下：

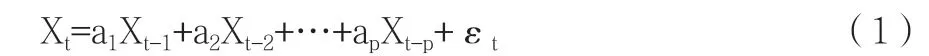
1.2 KNN 算法

KNN 算法是數據挖掘分類技術中最簡單的方法之一。所謂k最近鄰，就是k 個最近的鄰居的意思，說的是每個樣本都可以用它最接近的k 個鄰居來代表。KNN 算法的核心思想是如果一個樣本在特征空間中的k 個最相鄰的樣本中的大多數屬于某一個類別，則該樣本也屬于這個類別，并具有這個類別上樣本的特性。該方法在確定分類決策上只依據最鄰近的一個或者幾個樣本的類別來決定待分樣本所屬的類別。基于KNN 的方法依賴于歷史樣本中最有價值的少數樣本進行預報，而不是盲目地選擇時間上最近的樣本或全部可用樣本。

1.3 神經網絡模型

神經網絡模型主要有以下幾種類型：前向型、反饋型、隨機型和競爭型。

1.3.1 BPNN 模型

BPNN 是前饋神經網絡的一種，就是在前饋型網絡的結構上增加了后向傳播算法。后向傳播是用于訓練時網絡權值和閾值的調整，該過程是需要監督學習的。在訓練網絡階段，輸出與訓練集之間的偏差逐級向前傳遞，通過梯度下降等算法求得目標函數的取值，盡可能使得期望和輸出之間的誤差減小。

1.3.2 LSTM Networks

LSTM 是遞歸神經網絡（RNNs）的一種，在處理大復雜非線性系統問題時往往表現出優異的性能。相對于BPNN 在傳統的工程科學、簡單的時間序列中獲得應用，LSTM Networks 已經被廣泛應用在機器人控制、文本識別及預測、語音識別、蛋白質同源檢測等領域。LSTM 的優點在于解決了 SimpleRNN 梯度消失的問題，可以處理 long-term sequence，并在一定程度上緩和了梯度爆炸問題。其缺點是計算復雜度高，采用LSTM 的谷歌翻譯技術也只是7～8 層LSTM，LSTM 的實時應用較為困難。

1.4 BMA 集合預報算法

Leamer 最早地將貝葉斯理論引入到多模型集合預報，提出了Bayesian Model Averaging （BMA）模型，并指出BMA 能夠處理模型選擇所帶來的不確定性，避免過分依賴某單一的所選模型所帶來的計算誤差。以年降雨Q 作為預報變量，Tobs表示本年度以前實測降雨數據。設有m 個單一的降雨預報模型，某時刻的最優模型為M，則模型j為最優的概率為p(M=j|Tobs)，j=1,2,…m。根據貝葉斯理論，降雨量預報值Q 的后驗概率分布為：

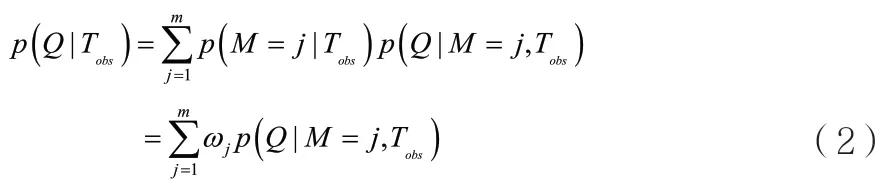
式中：p(Q|M=j,Tobs)為在給定數據集Tobs和最優模型為j 的條件下，預報變量Q 的后驗分布；ωj表示模型j 為最優的概率或模型j 的權重值，且滿足ωj=p(M=k|Tobs)，

由于模型結構等不確定因素的存在，事先并不知道哪個模型為最優模型，需要根據已知的實測與預報序列計算得出其為最優的概率。一般以BMA 算法所得預報變量分布的平均值作為BMA 確定性預報結果發布；其0.05 與0.95分位數上的值被認為是90%置信度的置信下限、上限。

2 數據介紹

2.1 數據準備

準備史灌河流域1956～2016年逐年降雨、徑流數據；史灌河流域代表站蔣家集的歷年逐月降雨、徑流數據。

為了得到月徑流量的的預報值，為調度計算及調度方案的制定提供數據支持，需要根據歷史降雨數據，篩選出不同頻率對應典型年，根據預報降雨量相應頻率、典型年，確定預報年的月分配比例系數。我國水文頻率計算一般采用P-Ⅲ型頻率曲線進行經驗頻率適線。

2.2 參數設定

（1）將AR 模型的回歸階數、KNN 的特征向量維數、BPNN 與LSTM 的輸入層節點數目統一設置為2，BMA 算法的集合預報成員數目為4；（2）依據現有1956～2016年的重點流域年降雨序列，按照75%∶25%的比例將完整系列劃分為訓練期、驗證期，對所建立中長期預報、集合預報模型進行率定與檢驗；（3）由于設定階數、特征向量維數、輸入層節點數等均為2。例如采用2015年、2016年降雨分別代入上述4 個預報模型預測2017年降雨，然后將2016年、2017年降雨分別代入預測2018年降雨，如此循環直到預測得到2030年降雨。

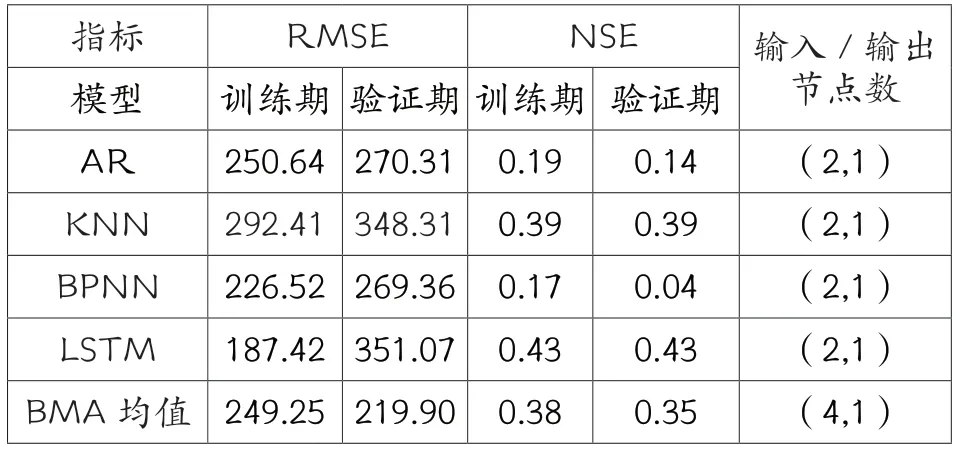
表1 史灌河流域降雨預報結果精度評定表

已確定BMA 集合預報成員數目為4，其各成員即上述四個中長期預報模型。依據現有1956～2016年的重點流域年降雨序列，按照75%∶25%的比例將完整系列劃分為訓練期、驗證期，對所建立集合預報模型進行率定與檢驗。約定目標函數為絕對誤差值。收斂條件為：（1）最大循環次數50000；（2）最小改進程度為0.1%。模型檢驗通過后，采用訓練好的BMA 模型綜合四個集合預報成員對2017～2030年逐年的年降雨預報結果，BMA 集合預報均值作為各年份集合預報的確定性結果，同時，其5%～95%置信區間的預報結果作為概率預報結果提供。

3 降雨預報結果

3.1 預報精度統計

根據《水文情報預報規范》，采用納什效率系數（確定性系數）、均方根誤差兩指標用于模型精度評定。整理分析各模型在訓練期、驗證期的預報結果評定結果，如表1所示。

從表1中可以直觀看到在采用RMSE 評價時，各模型在驗證期的RMSE 指標往往都比訓練期略高；而NSE 指標在驗證期更低，即各模型在采用訓練期的參數進行驗證時，往往會出現模型的模擬誤差放大的情況。BMA 集合預報算法在訓練期、驗證期的精度評定指標值的變化較小，其NSE 指標的變化為0.03，遠低于四個單一模型中的BPNN 指標的0.13，而RMSE 指標在驗證期比訓練期還要小，這也一定程度上說明了BMA 集合預報在中長期降雨預報中比傳統模型相對更穩定、可靠。

3.2 單一模型的預報結果

根據表1分析，認為相對其他三個模型來說，LSTM模型預報年降雨的過程與實測降雨的匹配程度更高，在評價指標上就直觀地反映為LSTM 的NSE 指標比其他幾個模型的NSE 指標更大。AR、BPNN 兩種常見的傳統預報方法所得到的預報過程與實測之間的差距相對更為明顯，表現在評價指標上就是NSE 指標更小、RMSE 指標相對更大。AR、BPNN 兩模型表現較差說明采用AR、BPNN 模型所默認存在序貫相關關系進行降雨預報，在中長期降雨預報這種紊動程度較高的應用場景是相對不那么適用的。而BPNN、LSTM 在驗證期的誤差放大得相對較為明顯，說明采用歷史樣本訓練的參數去預報未來降雨在一定程度上也是相對不夠可靠的。

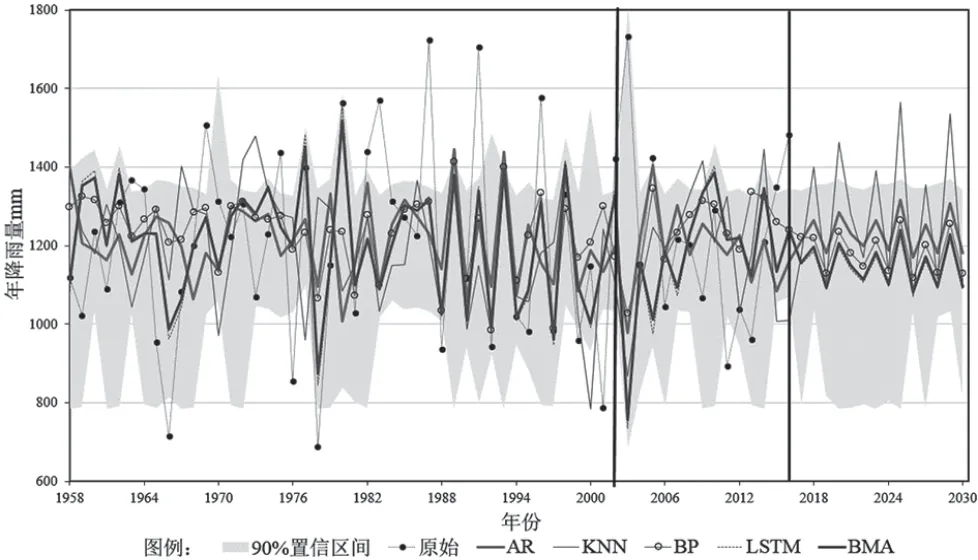
圖1 BMA 概率預報結果圖

3.3 BMA 集合預報結果

圖1展示了BMA 均值預報結果。BMA 集合預報結果的精度相對并不高，但是無論是其精度評定指標、驗證期預報的穩定性還是模型對年降雨過程的擬合精度，都不會出現明顯劣于單一模型的情況，采用BMA 算法能夠提高中長期降雨預報的精度與可靠性，尤其對預報結果可靠性程度的提升較為顯著。

由圖1、表1可知，率定期LSTM、BMA 均值預報結果的NSE 指標均達到0.4 以上，其中LSTM 率定期預報結果的NSE 指標達到0.43，RMSE 為四個模型、集合均值中的最小值為187.42。就預報精度而言普遍偏低，未能達到《水文情報預報規范》規定的預報作業要求。LSTM 模型預報精度相對最高，BMA 均值預報結果最為穩定，可以避免上述各集合預報成員出現預報可靠性降低的情況。

圖1中陰影區域表示的是BMA 集合預報的90%置信度區間，從其中可以觀察到BMA 的置信區間一定程度上能夠覆蓋各年度實際降雨量值，其覆蓋度指標為61.9%。這表明BMA 所提供的概率預報結果，具有可靠性。BMA集合預報的可靠性會隨著各單一預報模型精度的提高而顯著提升。

4 結語

該研究以1956～2016年蔣家集站的長系列降雨量數據為基礎，采用了AR、KNN、BPNN、LSTM 四種單一的預報模型，模擬進行年降雨預報；并引入BMA 算法綜合四種模型的預報結果，給出多模型集合預報的確定性及概率預報結果。經研究結果統計分析可知，單一的模型在進行中長期降雨預報的時候，往往會出現預報精度不高、預報誤差較大、驗證期預報結果穩定性較差的情況，這也是在中長期洪水預報應用中常會遇到的問題。研究發現，在采用BMA 集合預報算法對初步的預報結果進行綜合之后，算法所能夠給出的預報結果在模擬精度、驗證期預報結果穩定性上有了提高，說明多模型綜合對于提高中長期預報結果的可靠性程度是有積極意義的。

根據中長期預報技術精度要求，下一步需要引入由中國氣象局國家氣候中心氣候監測室提供的大氣環流指數、海溫等數據，優化篩選預報因子，進一步完善各中長期預報模型，提高模型預報精度與可靠性■