行為保險學系列（二十八）：記憶存量決定風險判斷偏差：綜合直接經歷與間接經驗

郭振華 上海對外經貿大學金融學院

除依賴自身經歷來感知風險之外，個體還通過觀察自己周邊他人遭受的風險事件來評估自己面臨的同類風險的大小，也就是說，間接經驗（曾經觀察到的他人遭受的風險事件）也會對自己的風險判斷造成一定的影響。例如，多數人有這樣的感覺，看到親戚朋友生病住院做手術，心里就有些打鼓，生怕自己也會經受同樣的疾病和手術。這種影響既是人們的直覺反映，也是理性的表現。風險發生的統計概率，就是依據對大量人群出事頻率進行統計的計算結果，其內在的假定是：對于相同種類的風險，每個人都有相同的出險概率。這一假定反映了理性人對他人遭受的風險事件會感同身受。

我們在本系列上一篇《記憶存量決定風險判斷偏差：僅考慮直接經歷》中，已經對個體依據直接經歷形成的記憶存量進行風險判斷作了系統分析，本文再加進個人的間接經驗，分析直接經歷和間接經驗對風險判斷偏差的綜合影響。

一、間接經驗對風險判斷的影響

間接經驗包括兩種，一種是觀察到別人遭遇風險，另一種是觀察到別人未遭遇風險，這兩種間接經驗都會對個體的風險判斷造成影響。

（一）觀察到他人遭遇風險對個體風險判斷的影響

個體觀察到的風險事件即間接經驗，來源包括親眼所見的風險事件和從媒體上看到的風險事件，親眼所見的風險事件通常是發生在親朋好友身上，或是在路上巧遇的風險事件。上述觀察到的風險事件都會存在個體的記憶中，進而對其未來風險判斷造成影響。但是，從影響程度來看，媒體上看到的和路上巧遇的風險事件，可能過一段時間就忘掉了，不會形成長久記憶，對未來風險判斷影響很小；而那些觀察到的發生在親朋好友身上的風險事件，個體受到的刺激或負面體驗感往往很大，很可能長久地留在人們的記憶中，對其未來風險判斷造成較大影響。

例如，目睹親朋好友的房子著火和在報紙上看到某遙遠地區的與自己毫無關聯的房子著火，對個體主觀火災概率的判斷，前者的影響要大得多，主觀概率更大。諾貝爾獎得主圣捷爾吉（因“與生物燃燒過程有關的發現，特別是關于維生素C和延胡索酸的催化作用”而獲得1937年諾貝爾生理學或醫學獎）曾說過：“如果我看到一個人正遭受苦難，我會被深深打動，并甘愿冒生命危險去救助他。但接下來，我卻能夠不帶感情地談論大城市可能的毀滅以及隨之而來的100萬人的死亡。”

也就是說，間接經驗對風險判斷的影響程度受到“情感距離”的影響。所謂情感距離，是指觀察到的風險事件受害者與自己（風險判斷者）的情感緊密程度，情感越緊密，情感距離越小。通常，情感距離越小，觀察到的風險事件例證對自己的風險判斷影響越大，越容易引發風險高估。或者說，間接經驗對個體風險判斷的影響會隨著情感距離的增大而衰減。那么，衰減速度如何變化呢？如果是直系親屬遭遇災難，個體會顯著地高估風險；如果是一般同事遭遇災難，個體感知到的風險就相對較小；如果是遙遠的與自己不相干的人遭遇災難，個體感受不到風險的存在。也就是說，隨著情感距離增大，個體的感知風險會迅速降低，情感距離過大，個體的感知風險幾乎為零。感知概率隨情感距離的變化曲線如圖1所示。

圖1中，在分界點，感知概率等于客觀概率；在分界點左側，感知概率大于客觀概率，表示情感距離很近的人群會高估風險；在分界點右側，由于情感距離較遠，人們會普遍低估風險；當情感距離很大時，人們幾乎感受不到這一風險的存在，感知概率為零。

（二）觀察到他人未遭遇風險對個體風險判斷的影響

觀察到他人未遭遇風險對個體風險判斷的影響機理，與上述觀察到他人遭遇風險對個體風險判斷的影響機理類似。即，看到他人未遭遇某種風險事故，已經遭遇風險的個體會調低自己的感知概率，未遭遇風險的個體則更加確信自己也不會遭遇同樣的風險事故。只不過，這種感受和影響是在潛移默化中完成的，個體甚至都感受不到。而且，個體受到的上述影響大小也與情感距離成反比，情感距離越小，受到的影響就越大。

二、直接經歷與間接經驗的綜合效應

（一）客觀概率不變，加進間接經驗的效果

對有損經驗人群來說，首先，僅考慮直接經驗時會高估小概率風險的出險概率；其次，小概率風險的間接經驗，絕大多數都是他人未發生風險事件的信息，因此，間接經驗會降低其感知概率。但是，由于間接經驗的影響受到情感距離的約束，不是所有他人的風險信息都會對其造成影響，而且影響程度會隨著情感距離的增大而迅速衰減。因此，在直接經歷基礎上增加間接經驗，有損經驗人群的感知概率會降低，但不會降低到客觀概率那樣低的程度，有損經驗人群仍然會高估概率。

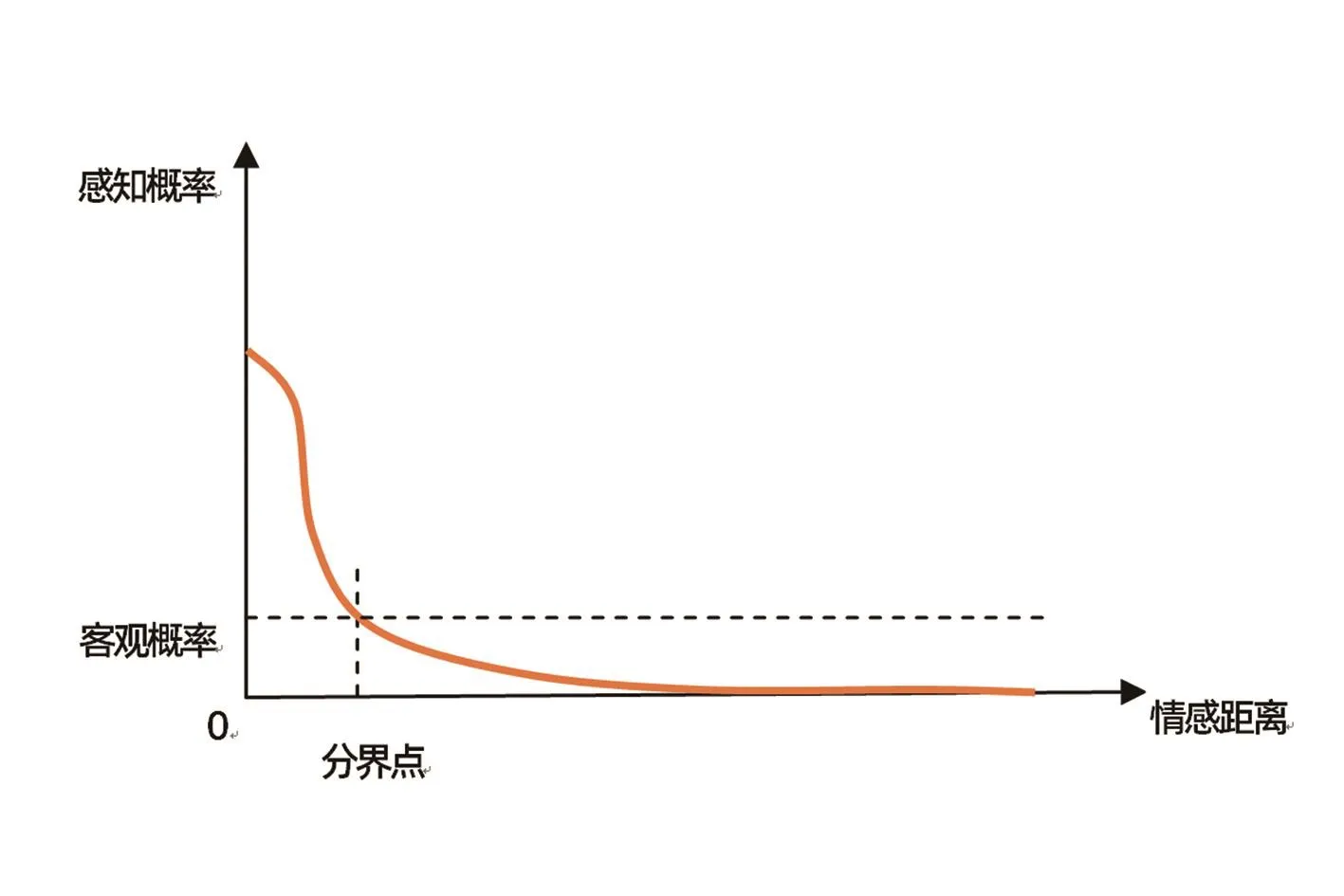
?圖1 情感距離對風險判斷的影響

對無損經驗人群來說，首先，僅考慮直接經驗時會低估小概率風險的出險概率；其次，對小概率風險進一步考慮間接經驗后，間接經驗會增加風險事件記憶的可得性或可提取性，提升人們的風險感知。但是，由于風險事件發生的隨機性，且其影響范圍受到情感距離的限制，其影響是嚴重不平均的。可以將所有人想象為一個湖泊的水平面，隨機發生的風險事件帶來的影響，像是水平面上被少量投進的石子泛起的漣漪。由于石子數量較少（小概率事件），漣漪波及范圍有限，導致只有少數人的感知概率會提升，其提升幅度取決于與石子投入點的距離。由此推斷，對于小概率風險，間接經驗將使無損經驗人群中部分人群的感知概率有所提升，感知概率有所提升的人數占比，隨著客觀概率的增大而增大；感知概率提升幅度則取決于情感距離，情感距離越近，提升幅度越大。

最終，對出險概率為P的小概率風險而言，在綜合考慮直接經歷和間接經驗后，與僅考慮直接經驗相比，人們的風險判斷偏差有所降低，但不會降低到與客觀概率相等的程度。第一，有損經驗人群的感知概率下降了一些，而有損經驗人群通常就是高估概率人群，他們的高估倍數都會有所降低，但仍然高于客觀概率。第二，無損經驗人群的感知概率有所提升，受風險距離遠近的影響，有的提高程度大（以至于從低估風險變為高估風險），有的提高程度小（以至于仍然低估風險），有的沒有變化、仍然為零。而無損經驗人群通常就是低估概率人群，因此，低估程度有所下降，他們的平均感知概率Pl從等于零變為大于零了，低估倍數P/Pl都會有所下降。第三，由于少數與遇險者情感距離很近的人會從低估風險變成高估風險，因此，高估風險者占比會有所增加，低估風險者占比會有所下降。

也就是說，與僅考慮直接經歷相比，加入間接經驗后，高估風險者占比有所增加且高估倍數有所降低，低估風險者占比有所下降且低估倍數也有所下降。

（二）客觀概率變化帶來的變化

根據《記憶存量決定風險判斷偏差：僅考慮直接經歷》中的相關數據，下面分析當客觀概率為0.0002、0.05、0.1和1時，直接經歷和間接經驗對風險判斷偏差的綜合影響，進而概括出客觀概率變化帶來的風險判斷偏差的變化規律。

當客觀概率為0.0002時，僅考慮直接經歷，99.88%的無損經驗人群低估概率，感知概率為零，低估倍數為無窮大；0.12%的有損經驗人群高估風險，感知概率為0.167，高估倍數為835。考慮間接經驗后：第一，0.12%的有損經驗人群，以及與其情感距離很近的原來低估風險的人，會變得高估風險，高估風險者占比略有擴大，若假定每個出險者會帶動與其情感距離最近的2個人高估風險，則高估風險者占比增加至0.36%；第二，由于高估風險者的間接經驗絕大多數都是不出險，以及部分低估者變成了高估者但高估程度較低，高估風險者的平均高估倍數（Ph/P）有所降低，但由于基數835倍很高，下降后仍然比較大；第三，高估風險者占比增加意味著低估風險者占比縮小，若高估風險者增加至0.36%，則低估風險者降至99.64%；第四，極少數與出險者情感距離較近的人群的感知概率有所上升，帶動Pl有輕微上升，低估風險者的平均低估倍數（P/Pl）從無窮大有所降低，但由于加入間接經驗后，大多數人仍然感受不到風險的存在，低估倍數較大。

當客觀概率為0.05時，僅考慮直接經歷，74.082%的無損經驗人群低估概率，感知概率為零，低估倍數為無窮大；25.918%的有損經驗人群高估概率，高估倍數為3.9。考慮間接經驗后：第一，25.918%的有損經驗人群以及與其情感距離很近的人會高估風險，高估風險者占比有所擴大，若假定每個出險者會帶動與其情感距離最近的2個人高估風險，則高估風險者占比增加至77.754%；第二，由于高估風險者的間接經驗多為不出險，以及部分低估者變成了高估者但高估程度較低，高估風險者的平均高估倍數（Ph/P）有所降低，高估倍數的基數為3.9，可能下降至2倍左右；第三，高估風險者占比增加意味著低估風險者占比縮小，若高估風險者增加至77.754%，則低估風險者降至22.246%；第四，由于客觀概率0.05比較大，與出險者情感距離較近的人群占比也很大，意味著幾乎所有未出險者的感知概率都會有所提升，帶動Pl大幅上升，低估風險者的平均低估倍數（P/Pl）從無窮大大幅降低，低估倍數較小，但仍存在一定的低估。

當客觀概率超過0.1后，僅考慮直接經歷，54.881%的人低估，45.119%的高估。綜合考慮直接經歷和間接經驗后，已經是隨處可見出險者了，在任一個體情感距離較近范圍內，其抽樣誤差大幅降低，風險判斷準確程度大幅提升，低估概率者和高估概率者的判斷都大幅逼近了客觀概率，預計高估概率者占比和低估概率者占比也越來越接近（雙方都接近50%），高估倍數和低估倍數都接近于1。

當客觀概率為1時，不確定性消失了，人們都變得能夠準確評估風險了，高估概率者占比和低估概率者占比均變為零。

綜合上述分析，加進間接經驗后，隨著客觀概率從零開始增長，相對于僅考慮直接經歷，高估概率者占比迅速增加（高估概率者曲線相對于僅考慮直接經歷更加向上傾斜），低估概率者占比迅速減少（低估概率者占比曲線相對于僅考慮直接經歷更加向下傾斜）。客觀概率超過0.1之后，人們的風險判斷開始逐漸趨于理性，但仍然不是高估就是低估，只是高估概率者占比和低估概率者占比都逼近50%。當客觀概率等于1時，人們變得能夠準確評估風險，高估概率者占比和低估概率者占比均變為零。由此，低估概率者占比曲線和高估概率者占比曲線的大致規律如圖2所示。

?圖2 高估（低估）概率者占比隨客觀概率的變化曲線

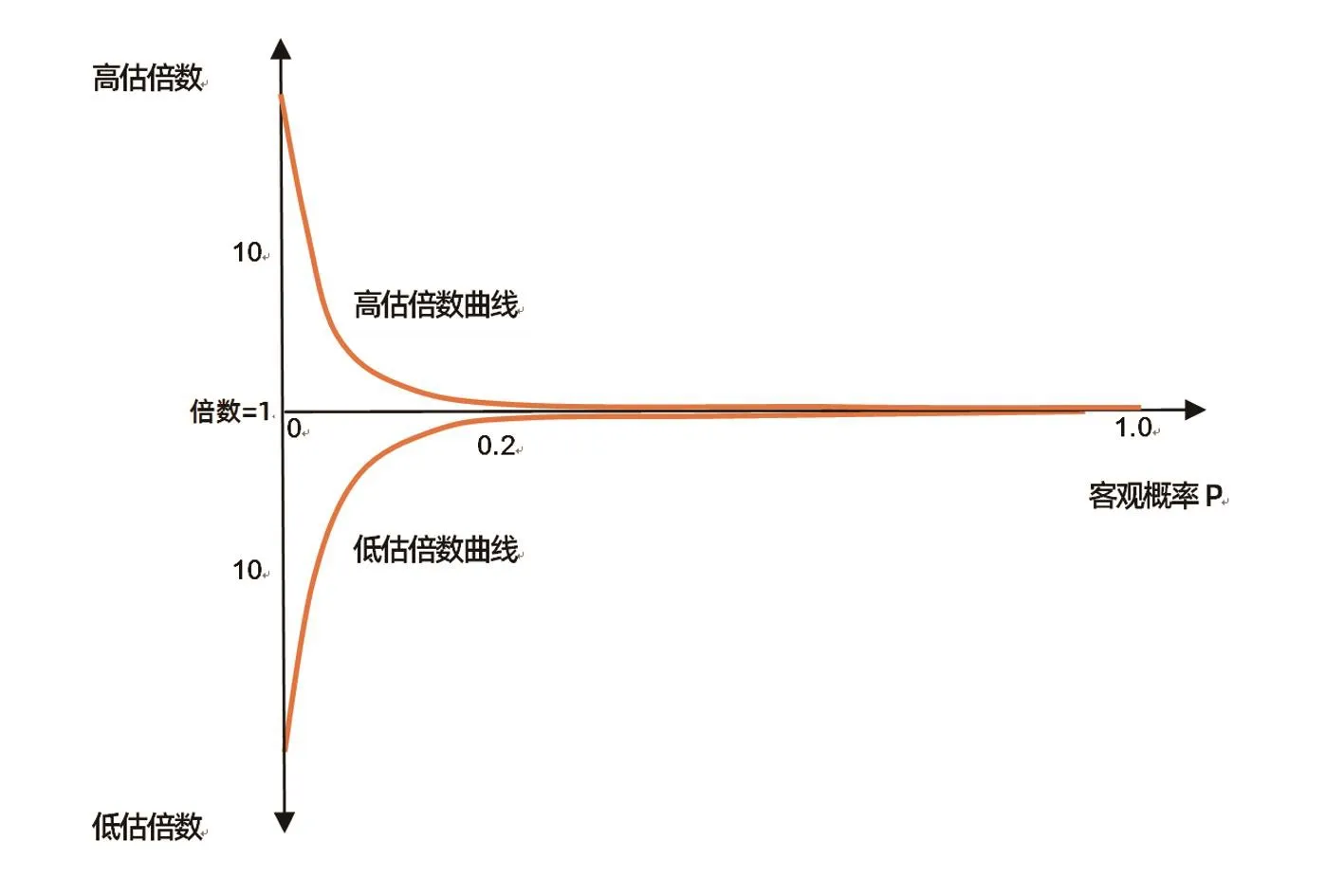
?圖3 高（低）估倍數隨客觀概率的變化曲線

同理，與僅考慮直接經歷相比，考慮直接經歷和間接經驗的雙重影響后，隨著客觀概率從0開始增長，平均低估倍數不再是無窮大了，平均高估倍數和平均低估倍數都會迅速降低。當客觀概率超過0.1后，風險判斷準確性大幅增加，平均高估倍數和平均低估倍數都迅速向1靠近。可以想象，當客觀概率為1.0時，不確定性幾乎消失了，風險事件的普遍發生形成普遍記憶，人們的感知概率與客觀概率會完全一致，風險判斷偏差消失了，高估倍數和低估倍數都等于1。由此，高估倍數和低估倍數的大致變化規律如圖3所示。

三、結論和分析特色

（一）結論

對保險所承保的小概率風險而言，客觀出險概率通常都低于0.2。因此，將圖2、圖3中客觀概率大于0.2的部分截去，就得到了將直接經歷和間接經驗一并考慮后，人們的風險判斷偏差規律，如圖4、圖5所示。

基本結論為：第一，人們不是高估風險，就是低估風險；第二，當客觀概率很低時，低估概率者占比很大且低估倍數很大，高估概率者占比很小且高估倍數很大；第三，隨著客觀出險概率的增加，高估風險者占比迅速增加，低估風險者占比迅速降低，高估倍數和低估倍數迅速降低；第四，客觀概率大致超過0.1后，高估概率者占比降低，低估概率者占比增加，雙方都向50%逼近；第五，隨著客觀出險概率增加，低估風險人群的低估倍數和高估風險人群的高估倍數都越來越小。

（二）上述分析的特色

長期從事個體風險決策或保險決策的讀者看到上述分析，多少會感到有些奇怪，因為上述分析給出了人群總體中的低估風險人群占比和低估程度、高估風險人群占比和高估程度，而不是個體的風險判斷結果。

其實這正是行為保險經濟學的優勢所在。即，與標準保險經濟學不同的是，行為保險經濟學認為人們的風險判斷結果不是同質的，或者說，對同樣的風險，不是所有人都有一致的風險判斷結果，而是有人高估有人低估。上述分析得到高估人群占比和高估程度、低估人群占比和低估程度，可用來進一步推導多少人保險需求旺盛、多少人需求疲弱，非常有利于分析保險市場的總體需求規律。

也就是說，行為保險經濟學破除了標準保險經濟學中的同質客觀風險假設或風險評估一致性假設，用更加符合現實的異質主觀風險來分析保險市場，可以得到更加符合現實的分析模式和結論。

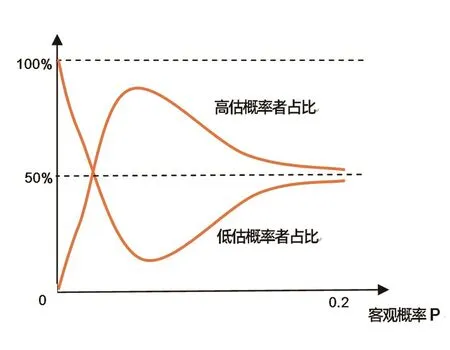
?圖4 高估（低估）概率者占比函數

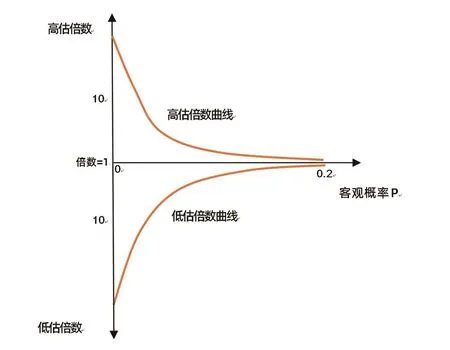
?圖5 高（低）估倍數函數