地震作用下鐵路貨車運行安全性研究*

吳 瀟， 丁軍君， 黃運華， 李 芾

(西南交通大學 機械工程學院， 成都 610031)

隨著我國鐵路網的迅速發展，車輛在運行中遇到地震的可能性越來越大。一旦車輛在地震中發生脫軌，造成的后果不堪設想。1976年唐山大地震，正在線路上運行的貨車有28列，其中5列貨車發生脫軌和傾覆，損失極為嚴重[1]。1995年1月的神戶大地震中，運行中的列車由于軌道振動而導致脫軌[2]。

為了減少此類事件的發生，國內外學者對地震中列車的運行安全性進行了大量的研究。Miura研究了地震中軌道變形對列車運行安全性的影響，得出軌道變形是造成列車脫軌的主要原因[3]。Tanabe建立了簡化分析地震條件的車輛-軌道耦合動力學模型，并利用新干線實車脫軌試驗驗證了模型的可靠性[4]。徐彩彩對地震條件下有砟軌道結構變形特性及列車安全性進行了研究[5]。肖新標等提出一個比較完善的車輛-軌道耦合動力學模型，利用EI-Centro地震波數據研究地震下高速列車的脫軌機理[6]。王開云等針對高速列車在地震中脫軌的因素提出一套評判地震條件下列車運行安全性的準則，并確定了列車運行安全域[7]。

但在以往的研究中沒有考慮輪軌匹配和摩擦系數對車輛運行安全性的影響。為此，文中建立地震作用下列車-軌道系統動力學模型，以C70貨車為研究對象，研究地震作用下，輪軌匹配和摩擦系數對車輛運行安全性的影響。

1 地震下車輛-軌道耦合動力學模型

地震作用下的車輛-軌道耦合動力學模型如圖1所示,軌道模型中軌道分為兩層，包括鋼軌與軌枕之間的扣件層和軌枕與路基之間的連接層，每層間采用彈簧和阻尼模擬。車輛模型簡化為一個車體，2個搖枕，4個側架，4個輪對，共11個剛體，48個自由度，各剛體自由度如表1所示。車輛模型中各部之間由彈簧阻尼連接，忽略模型中所有剛性元件的彈性變形。根據統計，在多次地震實例中，鋼軌連同軌枕產生嚴重的橫向彎曲變形，但路基并未出現破壞[8]，因此，文中將地震激勵直接加在軌枕上。

2 車輛運行安全性評判標準

在地震工況下，受橫向地震波的影響，運行中的車輛會發生劇烈的橫向振動，引起車體發生側滾，從而造成嚴重的輪重減載，與此同時，車輪出現爬軌或跳軌脫軌的現象，嚴重影響車輛運行的安全性并造成線路的嚴重損壞。傳統的車輛運行安全性評判指標包括脫軌系數Q/P、輪軸橫向力H、輪重減載率ΔP/P。但是在地震作用下車輛的運行狀態與正常運行狀態相差很大，車輪不斷跳離鋼軌并與鋼軌頻繁發生撞擊。為此，橫賴景司提出了JNR跳軌評價準則，根據跳軌脫軌時間進行評判，標準規定脫軌系數超限時間不得超過0.05 s[9]。此外，一些學者將輪軌抬升量作為評價脫軌指標。Ishida 等經過大量的試驗得出當脫軌系數超過0.8的作用時間在15 ms以內，且車輪抬升量不超過1 mm，列車的安全性和穩定性均是有保證的[10]。Nishimura提出列車脫軌的評判邊界為：車輪相對鋼軌垂向抬升量達到20 mm，車輪相對鋼軌外側的橫向位移量達到30 mm[11]。

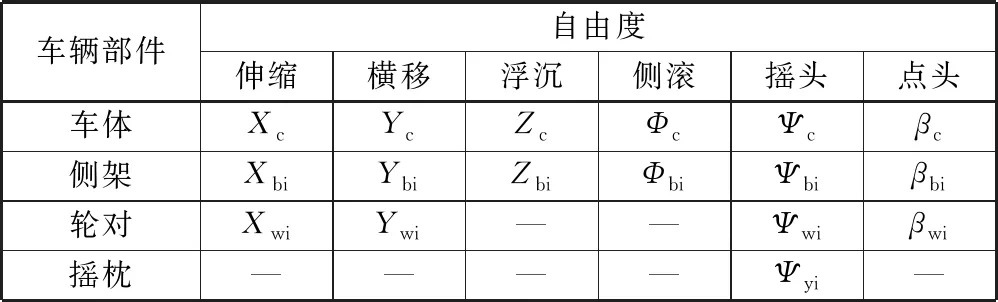
表1 車輛動力學模型的自由度

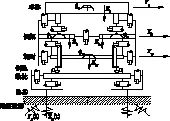
圖1 地震作用下車輛-軌道耦合動力學模型

對于地震這種特殊工況，文中采用脫軌系數Q/P、脫軌系數超限時間JNR、輪軸橫向力H、輪重減載率ΔP/P、輪對抬升量Dz、輪軌相對橫移L等6種評價指標，研究地震波影響車輛運行安全性的主要因素以及在相同地震激勵下，鋼軌廓形和輪軌摩擦系數對車輛運行安全性的影響。根據GB 5599-1985[12]的規定和相關學者的研究，車輛運行安全性限值如表2所示。

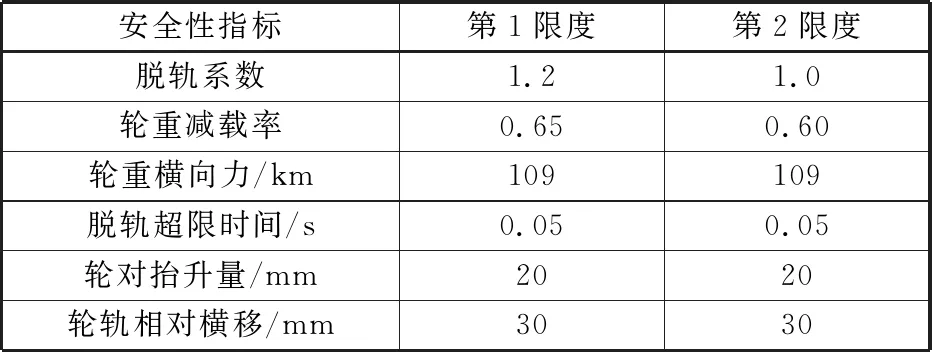
表2 車輛運行安全性指標限值

3 地震波影響車輛運行安全性的因素

地震對車輛運行安全性的影響主要源于地震橫波，在不考慮行波效應的情況下，將地震波簡化為垂直于車輛運行方向的5個周期的正弦波，地震波位移和加速度施加于軌枕。依據以上評價指標，分析C70貨車在不同頻率、不同震幅的地震波作用下運行的安全性。圖2給出了車輛在60 kg/m鋼軌(以下簡稱60軌)上以不同速度運行時，不同頻率和震幅對應的脫軌邊界，設定車輛速度為60～100 km/h，地震波頻率為1.0～4.0 Hz，地震波震幅為0～160 mm。圖中A為脫軌區，B為安全區。由圖可知車輛運行速度對地震中車輛的運行安全性影響不大，車輛運行安全性主要受地震波幅值和頻率的影響。

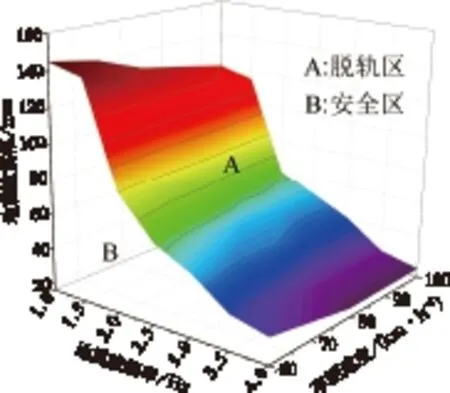
圖2 不同速度運行時頻率和震幅對應的安全邊界

4 鋼軌廓形對車輛運行安全性的影響

地震中影響車輛運行安全性的因素除地震波幅值和頻率外，惡劣的輪軌關系也會增大車輛發生脫軌的風險。為比較鋼軌廓形對車輛運行安全性的影響，仿真過程中車輛以80 km/h的速度在直線上運行，軌道激勵為美國5級譜；限于篇幅地震波震幅設為20 mm，頻率采用1.0 Hz、1.5 Hz、2.0 Hz、2.5 Hz、3.0 Hz、3.5 Hz和4 Hz，7種地震波所對應的峰值加速度和烈度等級[13]如表3所示。

不同鋼軌廓形條件下，脫軌系數隨地震波頻率的變化曲線如圖3所示。車輛的脫軌系數隨地震波頻率的增加而逐漸增大。當地震波頻率為2.7 Hz時，地震烈度等級為Ⅸ級，車輛在60軌上運行的脫軌系數達到安全限值；而車輛在60N軌上運行的脫軌系數達到限值時，地震波頻率為3.3 Hz，地震烈度等級為Ⅹ級。因此，在地震強度相同的情況下，車輛在60N軌上運行的安全性較好。

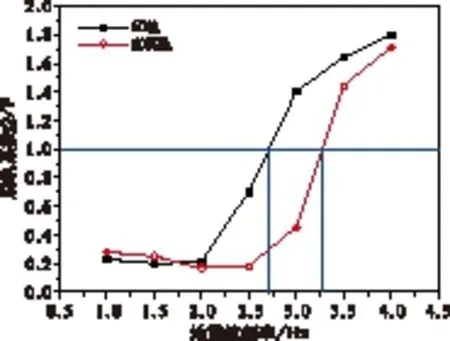
圖3 不同廓形的脫軌系數對比

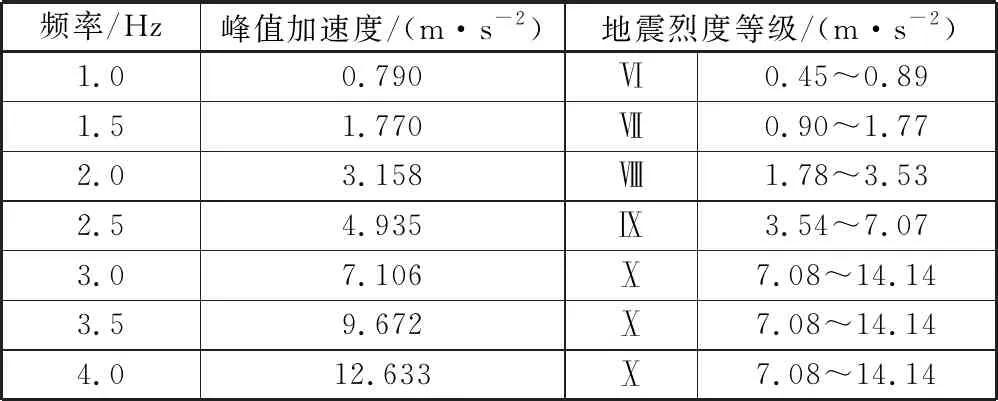
表3 不同頻率地震波的峰值加速度及烈度等級

圖4中描述了輪軸橫向力隨地震波頻率的變化曲線。當地震頻率為2.6 Hz時，60軌的輪軸橫向力率先達到輪軸橫向力限值，而60N軌的輪軸橫向力達到限值時地震波頻率為3.1 Hz。因此，車輛在60軌上運行時允許的最大地震烈度為Ⅸ級，而在60N上運行時允許的最大地震烈度為Ⅹ級。這導致在地震波強度相同的情況下，60軌受損比60N軌更嚴重。

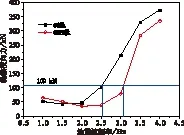
圖4 不同廓形的輪軸橫向力對比

由圖5可知，在不同鋼軌條件下，地震波頻率為1.5 Hz時，車輛在兩種鋼軌上運行的輪重減載率全部超過第一限值，這是由于車體側滾的頻率為1.7 Hz，與地震波頻率接近，導致車輛發生共振，從而引起輪重嚴重減載，車輛劇烈顛簸。地震波頻率大于1.5 Hz時，相比60N軌，車輛在60軌上運行的輪重減載率較大；當地震波頻率大于2.9 Hz時，60軌的輪重減載率超過第2限值；地震波頻率為3.0 Hz時，60軌相比60N軌，輪重減載率增長了35%。因此車輛在60N軌上的運行平穩性稍好。

在地震環境中，車輛受橫向地震波作用，輪軌出現較大的相對橫移，車輪出現較大的抬升，從而引起車輪出現爬軌或跳軌的現象。在這一過程中規定車輪抬升量超過20 mm，同時輪軌相對橫移超過30 mm，即認為車輛發生脫軌。地震波作用下，車輪抬升量和輪軌相對橫移隨地震波頻率的變化曲線如圖6所示，圖a中車輛在60軌上運行時車輪抬升量較大，地震波頻率為3.85 Hz時，60軌的車輪抬升量達到20 mm安全限值；圖b中地震波頻率超過3.5 Hz后，60軌的輪軌相對橫移量迅速增大，且于地震波頻率為3.8 Hz時達到30 mm安全限值。由此可見，在地震波頻率為3.8 5Hz時，在60軌上運行的車輛率先發生脫軌。

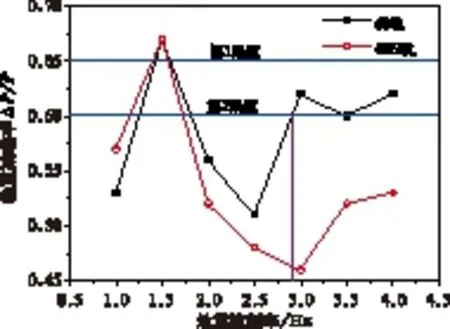
圖5 不同廓形的輪重減載率對比

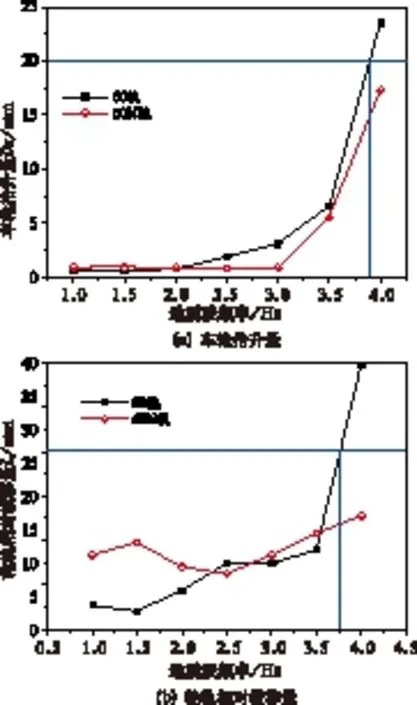
圖6 地震作用下輪軌幾何接觸關系

5 輪軌摩擦系數對車輛運行安全性的影響

不同的外部環境可導致輪軌間摩擦系數不同，軌面有油污輪軌摩擦系數為0.15，受雨雪影響輪軌摩擦系數為0.2，軌面潤濕輪軌摩擦系數為0.25，軌面干燥清潔輪軌摩擦系數為0.4[14]。在地震波相同的情況下，依據脫軌系數Q/P、輪重減載率ΔP/P、輪軸橫向力H評判摩擦系數不同時車輛在60N軌上的運行安全性。

圖7為車輛運行安全性評判指標隨地震波頻率變化的曲線，輪軌摩擦著系數越小，其脫軌系數越大；在地震波頻率大于3.0 Hz時，摩擦系數0.15和0.2對應的脫軌系數急劇增大，頻率為4.0 Hz時達到最大值，分別為3.25和3.06。圖b中，地震波頻率為4 Hz時，摩擦系數0.15和0.2對應的輪重減載率為1，此時車輪踏面與鋼軌分離。圖c中輪軸橫向力隨地震波頻率增大而增大，摩擦系數0.15和0.2對應的輪軸橫向力最大值分別為731.57 kN和564.83 kN。

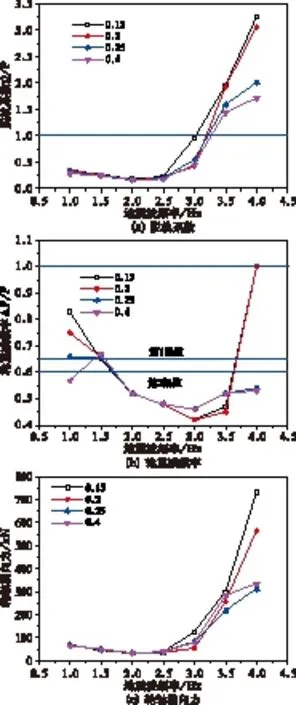
圖7 運行安全評判指標

地震波頻率為4.0時，摩擦系數0.15和0.2對應的脫軌系數和輪重減載率對時間的變化如圖8所示，摩擦系數為0.15和0.2時，第1輪對右輪的脫軌系數分別在2.77 s和2.96 s超限，持續時間均為0.07 s，均已超過JNR標準規定的0.05 s限值；對應的輪重減載率均到達1，即輪軌分離，且輪軌分離超過1 s，根據JRN脫軌準則，此時車輛已經脫軌。可見輪軌摩擦系數越小，相同地震波作用下脫軌的危險性越大。

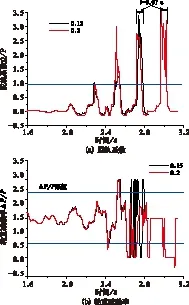
圖8 脫軌指標時間歷程

6 結 論

文中建立了地震作用下的車輛-軌道耦合地震動力學模型，將地震波簡化為正弦波并作為外部激勵施加于軌枕，對地震作用下車輛的動態響應和運行安全進行了數值分析，得出結論如下：

(1) 在相同強度地震波作用下，相比60N軌，60軌的脫軌系數、輪重減載率、輪軸橫向力、車輪抬升量以及輪軌相對橫移較大；地震烈度為Ⅹ級時，運行在60軌上的車輛已經發生脫軌；此外，相同地震強度下，60軌受到的破壞更嚴重。

(2) 地震波頻率與車體側滾頻率接近時，車體易發生共振現象，導致車輛發生嚴重的輪重減載，使得車輛產生劇烈顛簸，嚴重影響車輛運行平穩性。

(3) 相同地震工況下，輪軌摩擦系數越小，車輛運行安全性越差，在軌面有油污和受雨雪影響時最易脫軌。