輸變電建設工程政處風險處理能力區域性評價

王 昊, 沈 昱, 張秋實

(1.國網江蘇省電力有限公司，江蘇 南京 210024；2.武漢科迪奧電力科技有限公司，湖北 武漢 430223)

0 引 言

隨著科學技術和社會經濟的迅猛發展,電能開始不斷應用于各行各業,輸變電工程的建設任務也愈加繁重,工程建設周期不斷增長,參與主體逐漸增多,組織關系越來越復雜,諸多的制約因素開始出現并影響著項目建設正常運行。所以,為了降低輸變電項目風險發生的概率以及風險可能造成的損失,必須加強對風險的管理評估[1]。

近年來,國內外對影響電網建設正常進行的各種風險的評估一直非常重視,并且取得了一些突破性的進展。其中在線路運行方面,Tom B.等[2]建立了架空線路覆冰風險的評估分析模型,并運用故障樹分析法,實現了對由覆冰引起的線路斷線與桿塔倒塌等風險的有效評估。鄧紅雷等[3]提出了基于層次分析法與熵權法的架空線路綜合運行的風險評估模型。劉珂宏等[4]以架空輸電線路的以往故障缺陷的經驗為依據,將輸電線路不同部位的狀態通過數值量化了出來,并以此為依據總結了風險評價結果的概率值,從而建立了架空輸電線路的風險評價模型。任俊等基于[5]G1法和層次分析法對電網的信息系統進行了風險的評估。鐘銀超等[6]提出了基于模糊層次分析法的電網安全風險的客觀評價模型。胡文平等[7]提出了基于云理論的預測模型,并將其運用于輸變電設備故障率的分析,并通過效用理論確定了比較完備的電網綜合風險評估指標體系[7]。

但現有的大多數風險評價的研究都是按照同一標準對各地區的風險進行評估,沒有考慮風險的區域性差異,尤其是政處風險,其區域性差異尤其明顯。政處風險是指由于國家和政府的法律法規、政策的變化以及政府的行為或因素而導致建設項目延期投產的風險。它作為電網建設過程中的常見風險,也是制約電網建設正常運行的諸多因素之一。區別于其他種類的風險,政處風險在不同地區發生的可能性、發生的頻率以及發生后產生的影響,都因各地區對政處風險處理能力的不同而存在著明顯差異[8,9]。LEC評價法等傳統的風險評估方法難以對其進行合理的評價,從而導致在項目的管理決策過程中,難以對各項政處風險造成的影響采取合理的預防和應對措施[10]。

針對上述問題,本文提出了將LEC評價法與層次分析法相結合的方法,以LEC評價法的客觀評價為基準,通過層次分析法建立各地區政處風險處理能力的評價模型,對江蘇省的部分縣市的政處風險處理能力進行定量的評估和排序。

1 評估方法的理論基礎

1.1 LEC評價法

LEC評價法是對危險性作業環境中的危險源進行半定量的安全評價方法。該方法對作業環境中的各風險進行評價主要是采用與系統人員傷亡相關聯的三個指標。它們分別是:L——風險發生的可能性;E——一定作業數量下風險發生的次數;C——風險發生后導致的人員傷亡情況。通過對L、E、C三個數據的計算分析,可得到各風險的固有風險值進而確定風險的等級,這里若將C定義為風險發生后對工期造成的延誤程度并確定賦值標準,同樣可以利用該方法計算政處風險的固有風險值和風險等級,風險值的計算公式為:

D=L×E×C

其風險值D越大,風險的等級就越高,相應的便應該引起足夠的重視。

1.2 層次分析法

層次分析法是電網建設風險管理中常用的方法之一,它可以將定性問題予以定量化的解決。該方法的主要思想是把復雜的安全問題層次化,將決策問題按總目標、屬性、方案的順序分解為不同的層次,從而構建一個層次分析的結構模型。然后,依據各元素之間的重要性關系,得出它們之間的相對權數。最后遞階歸并,確定各方案的優劣次序,并為最后的決策提供依據[11-15]。其具體步驟為:

(1)建立層次結構模型:確定評價目標,在目標的基礎上明確評價目標的準則和方案,從而構建合理的層次結構。

(2)構建兩兩比較矩陣:根據建立的層次模型,并參考往年的項目建設資料,請專家對每層各因素進行兩兩比較評分,建立各個層次的兩兩比較矩陣。

(3)層次單排序及一致性檢驗:求解各兩兩比較矩陣的優先級向量,并檢查各兩兩比較矩陣的一致性是否滿足要求。

(4)層次總排序:依據各層次元素的相對權重,進而計算不同方案對總目標的權重。

其中根據判斷矩陣,計算優先級向量的公式為:

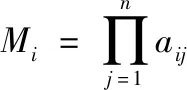
(1)

(2)

(3)

一致性檢驗的計算公式為:

(4)

(5)

2 層次分析法-LEC評價法組合優化

LEC評價法是電網風險評價的常用方法,它不需要建立復雜的評價模型,并且在評價的過程中不需要收集相關風險變量的經驗數據,便可以對風險進行客觀的量化,但該方法卻很難將某種風險的區域性差異以及不同風險之間的聯系量化地體現出來。而層次分析法作為一種多目標、多因素的決策分析方法,它可以將復雜的問題層次化、簡單化,并綜合各個能夠對目標造成影響的因素，對最終的結果進行定量的評價,所以該方法在電網建設風險評估方面有著重要的意義。然而,該方法雖然具有數據獲取簡便、易于理解等優點,但在建立兩兩比較矩陣以及根據評價目標確定結構模型的時候,往往很容易受到以往的項目經驗以及參與評價者的主觀選擇、想法的干擾,從而導致決策目標的結果的準確性不足。

針對上述兩種方法的缺陷,本文將LEC評價法與層次分析法相結合,以LEC法客觀量化得到的風險值D作為參考,為層次分析法判斷矩陣的主觀量化提供依據,主客觀互補,提高了各層次評價結果的準確性,同時有效地避免了元素過多而導致的數據失真。采用該方法對不同地區的各個政處風險進行量化的評估,得到各個地區的政處風險處理能力的差異,具體基本流程如圖1所示。

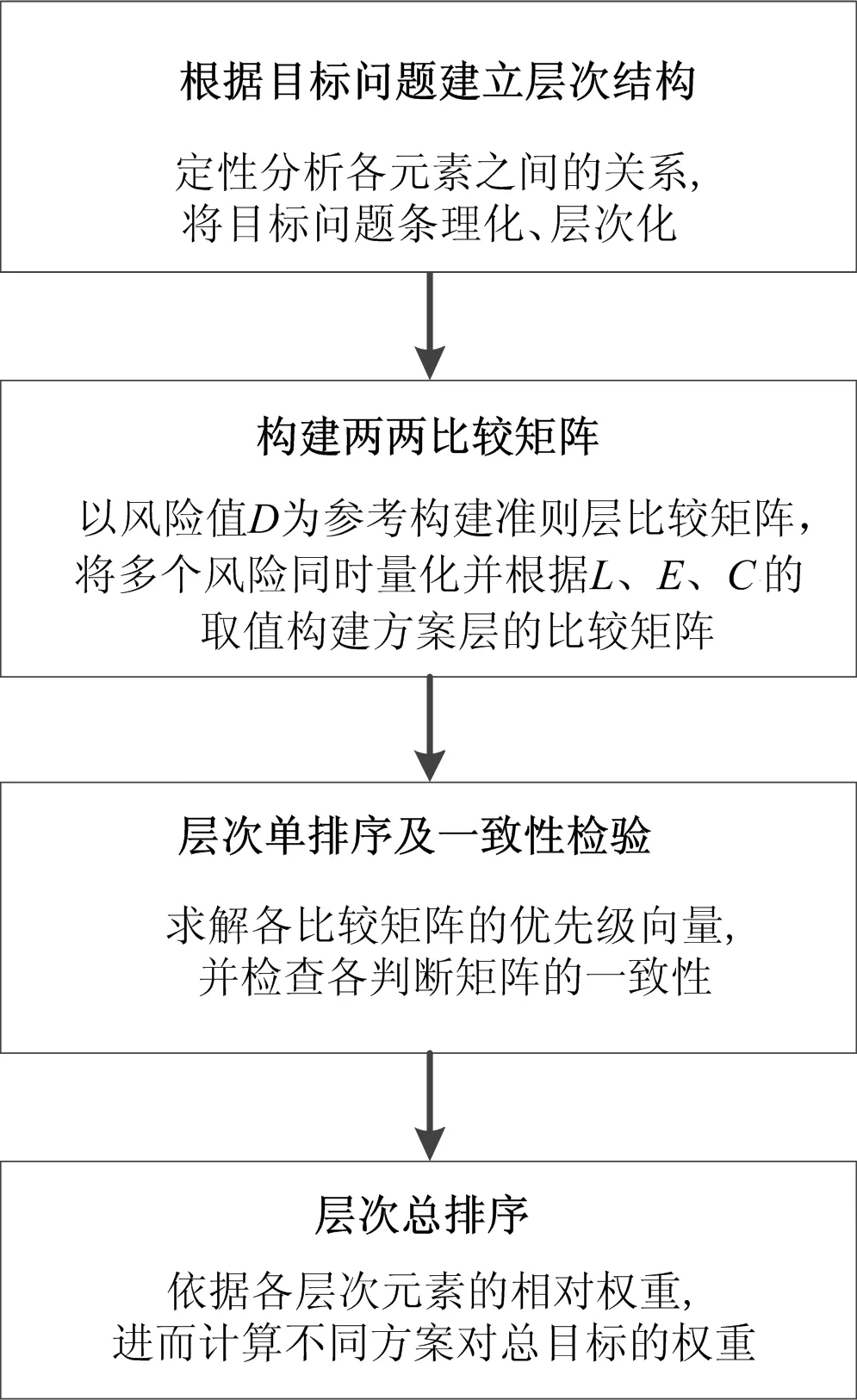
圖1 層次分析法-LEC評價法基本步驟

3 各地區政處風險處理能力的評估

以江蘇省的部分縣市為例,將LEC評價法與層次分析法結合起來,對其政處風險的處理能力進行區域性評估。

3.1 建立層次結構模型

采用層次分析法與LEC法相結合的方法,對各地區政處風險的處理能力進行區域性評估,可以將多個風險項進行同時量化,所以在結構模型中,準則層為各政處風險項,方案層為江蘇省的不同縣市,目標層則表示為不同地區對政處風險處理能力的權重,其層次結構圖模型如圖2所示。

圖2 層次結構模型圖

在該案例中,準則層的風險項選用“新建項目征地,施工遇到阻撓”,“新建項目征地(農用地、綠地)”,“新建工程施工許可證手續未獲受理”,“電纜穿越鐵路施工”,共4項,分別用A1、A2、A3、A4表示。方案層取江蘇省的徐州、南京、蘇州三個市,分別用B1、B2、B3表示。

3.2 構建兩兩比較矩陣并進行一致性檢驗

以LEC評價法得到的各政處風險項的固有風險值D為依據,建立準則層的兩兩比較矩陣,并參考LEC法中L、E、C參數的取值,請專家在上層元素的基礎上構造方案層的兩兩比較矩陣,其中矩陣的標度及含義見表1。

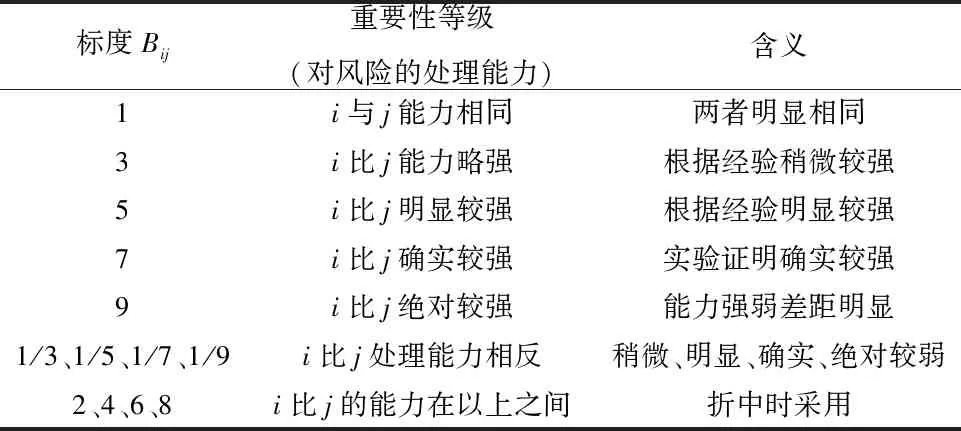
表1 判斷矩陣的標度及含義

并通過MATLAB編程,由各層元素的相對權重得到其對應的優先級向量并計算對目標層的綜合權重如下所示:

準則層的兩兩比較矩陣:

對于風險A1,B1、B2、B3之間的兩兩比較矩陣:

對于風險A2,B1、B2、B3之間的兩兩比較矩陣:

對于風險A3,B1、B2、B3之間的兩兩比較矩陣:

對于風險A4,B1、B2、B3之間的兩兩比較矩陣:

最后通過判斷矩陣的優先級向量,計算B1、B2、B3三個市對風險的處理能力:

B1:1/10×1/15+1/4×2/15+1/4×4/15+1/9×8/15=152/1 350=0.11

B2:3/5×1/15+7/12×2/15+3/8×4/15+1/3×8/15=534/1 350=0.40

B3:3/10×1/15+1/6×2/15+3/8×4/15+5/9×8/15=592/1 350=0.44

對于各區域來說,結果的權重越大,表示對風險的處理能力越強,風險在該地區造成的影響越小,所以三個地區的政處風險處理能力的比較結果為:B3>B2>B1,即政處風險處理能力由強到弱依次是蘇州市、南京市、徐州市。

一致性檢驗:

所以其一致性滿足要求。

4 結 論

本文通過LEC評價法與層次分析法相結合的綜合評價方法,以江蘇省的3個縣市為例對其政處風險處理能力的差異進行了量化處理,并建立了比較完備的風險評估模型,規避了傳統層次分析法容易受到主觀影響缺點,同時,也有效地克服了LEC評價法難以將政處風險區域性差異體現出來的不足,得到了一種新型的評價體系,為項目的管理決策提供科學的依據。最后的評價結果也充分證明了該方法是合理準確的,說明了此方法在政處風險區域性差異的分析方面存在著一定的參考價值。