城市暴雨強度公式理論頻率曲線選擇研究
肖友淦
(福州城建設計研究院有限公司 福建福州 350001)
0 引言
2013年3月25日,國務院正式發布了《國務院辦公廳關于做好城市排水防澇設施建設工作的通知》(國辦發〔2013〕23號),明確要求“各地區要結合氣象、水文資料,對現有暴雨強度公式進行評價和修訂”。在采用年多個樣法編制城市暴雨強度公式時期,經驗頻率的計算和理論頻率曲線的選擇兩大問題引發了學術界極大的爭議。隨著《室外排水設計規范》GB50014-2006(2016年版)(以下簡稱新版排水規范)的發布,要求新編暴雨強度公式采用年最大值法選樣,并有如下規定:“選取的各歷時降雨資料,應采用經驗頻率曲線或理論頻率曲線加以調整,一般采用理論頻率曲線,包括皮爾遜Ⅲ型分布曲線、耿貝爾分布曲線和指數分布曲線。根據確定的頻率曲線,得出重現期、降雨強度和降雨歷時三者的關系,即P、i、t關系值。”可以看出,新版排水規范用于暴雨強度公式參數擬合的降雨資料實際有4種情況:①采用經驗頻率曲線,對原始降雨資料進行目估適線;②采用皮爾遜Ⅲ型分布曲線調整過的降雨資料;③采用耿貝爾分布曲線調整過的降雨資料;④采用指數分布曲線調整過的降雨資料。本文將論述這4種方法的優劣,并提出最合適的頻率分布曲線及其快速計算方法。
1 經驗頻率曲線
年最大值法時,經驗頻率(即年頻率)計算公式一般采用[1-2]:
式中:P——年頻率;
m——資料由大到小的序列;
N——資料年數。
表1為某城市1980年~2013年5min歷時的降雨資料。假設該市暴雨強度公式的編制時間為2014年,那么,該市用于暴雨強度公式編制的5min歷時降雨資料應為1980年~2013年(其中1999年、2000年無資料)資料,此時降雨經驗頻率和重現期如表2所示。假設該市暴雨強度公式的編制時間為2002年,那么,該市用于暴雨強度公式編制的5min歷時降雨資料應為1980年~2001年(其中1999年、2000年無資料)資料,此時降雨經驗頻率和重現期如表3所示。兩次暴雨強度公式編制時同一降雨量代表的重現期對比如圖1所示。
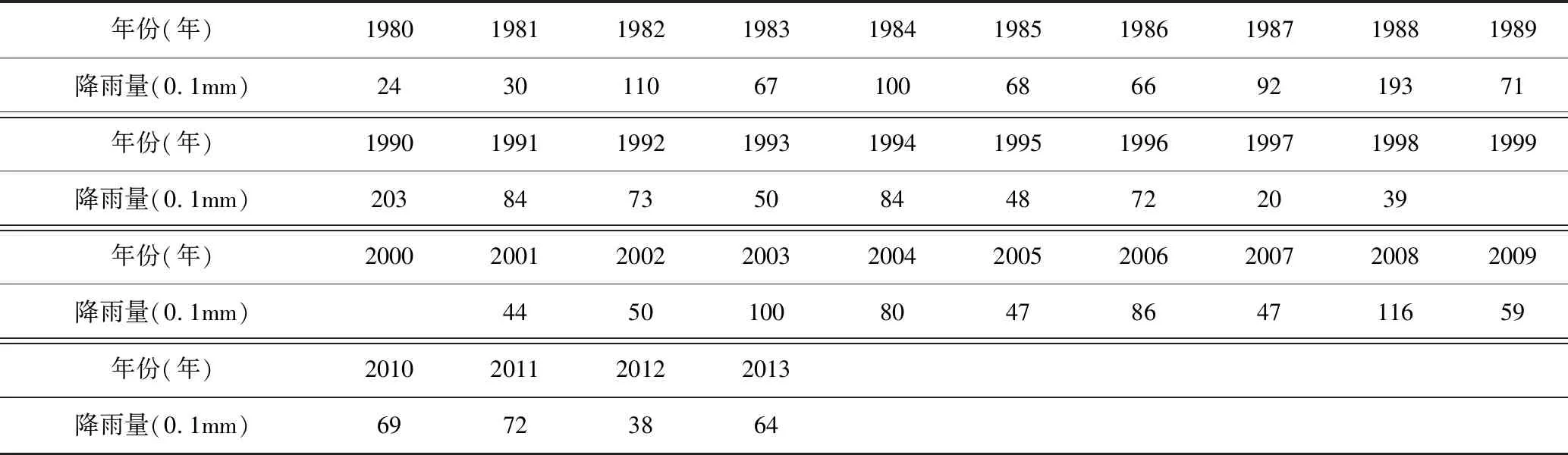
表1 1980年~2013年5min歷時降雨資料
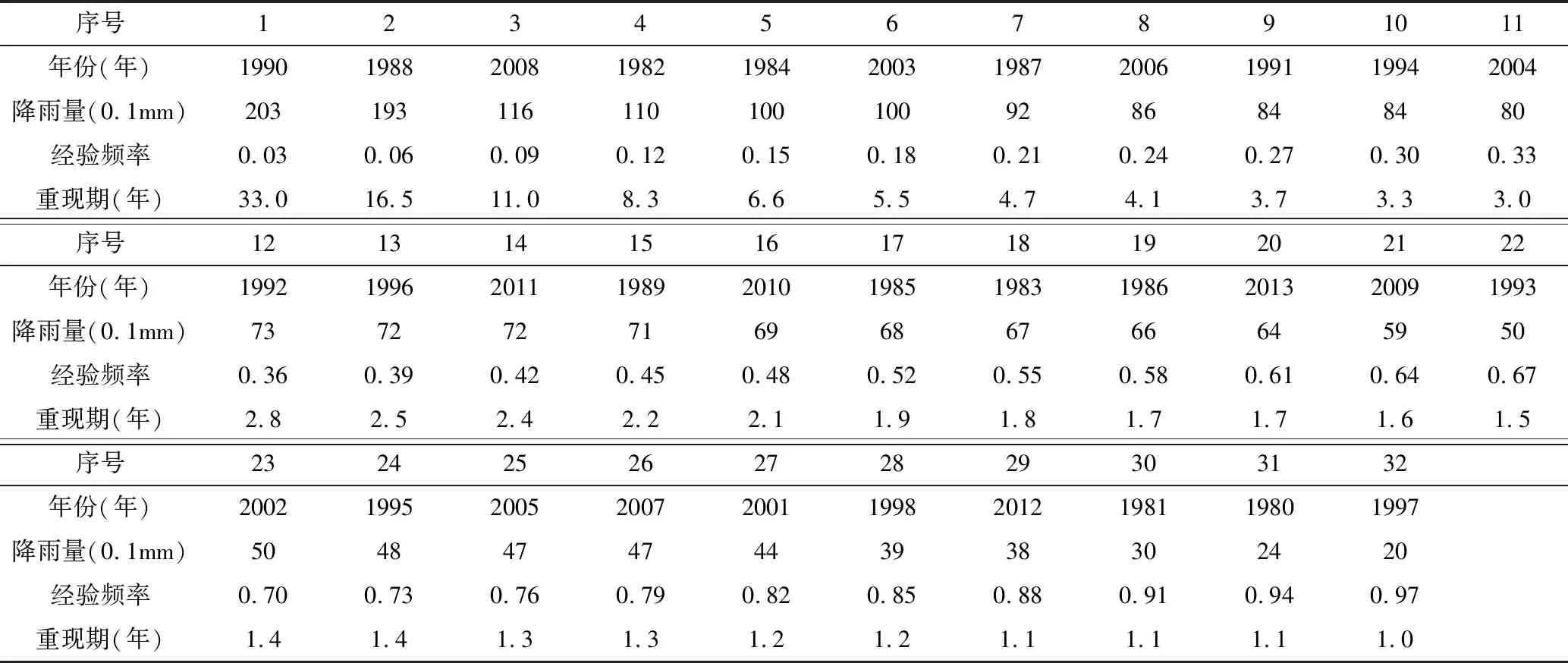
表2 1980年~2013年5min歷時降雨經驗頻率
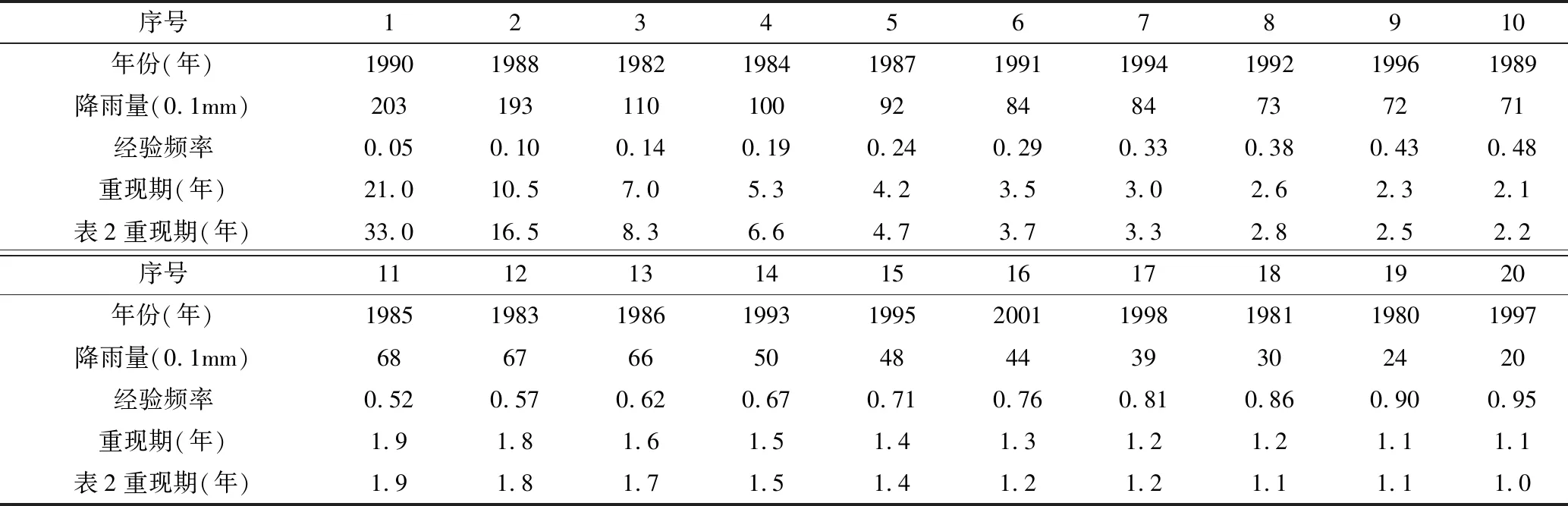
表3 1980年~2001年5min歷時降雨經驗頻率
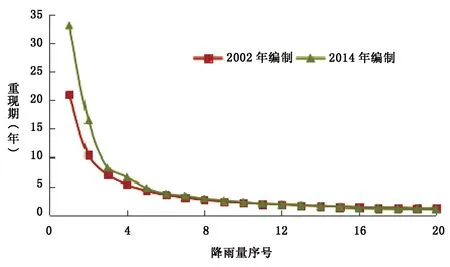
圖1 同一降雨量代表的重現期對比圖
從圖1可以看出,該方法與選用數據年限具有很大關系。如果在2002年暴雨強度公式編制時,直接采用經驗頻率曲線而不進行理論頻率曲線修正,那么在高重現期時的降雨數據將偏大,低重現期時的降雨數據將偏小。例如,同樣是20.3mm降雨,在2002年編制時為21年一遇降雨,在2014年編制時為33年一遇降雨,而2014年編制時的21年降雨重現期對應的雨量應介于19.3mm和20.3mm之間。
同時,采用經驗頻率曲線也難以進行頻率曲線的外延。例如,利用30年的數據,預測重現期為100年的暴雨,這是不切實際的。因此,盡管經驗頻率曲線具有方法簡單的特點,但在城市暴雨強度公式編制過程中,建議降雨資料應采用理論頻率曲線調整,然后進行暴雨強度公式參數擬合。
2 三種理論頻率曲線比較
一般采用的理論頻率曲線為皮爾遜Ⅲ型分布曲線、耿貝爾分布曲線和指數分布曲線。其中,皮爾遜Ⅲ型分布曲線累積分布函數為[1]:
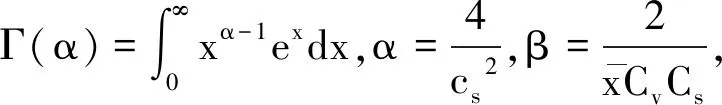
xp——樣本值;

Cv——樣本變差系數;
Cs——樣本偏差系數。
當Cs=2時,皮爾遜Ⅲ型分布曲線累積分布函數變為[3]:
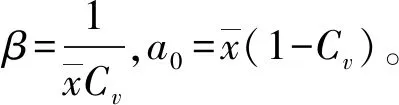
該式為指數分布曲線的累積分布函數,有解析解。
當Cs=1.1395時,皮爾遜Ⅲ型分布曲線累積分布函數變為[3]:
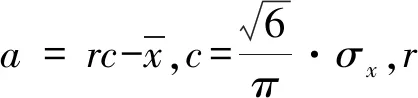
因此,指數分布曲線和耿貝爾分布曲線實際上是皮爾遜Ⅲ型分布曲線在Cs=2和Cs=1.1395的特例。理論上利用皮爾遜Ⅲ型分布曲線對降雨數據進行調整,能夠得到比指數分布和耿貝爾分布更好的結果。但以往多數城市在暴雨強度公式的編制中均采用指數分布曲線,其原因正如鄧培德先生所指出的:“皮爾遜Ⅲ型模型是三參數公式,在理論上可以概括耿貝爾分布與指數分布,但現有水文資料實在不夠,不可能算得可靠的偏態系數,特別是高偏態與高重現期時不太合適,乙形分布是高偏態的極端形態,就較難適合,此外三參數擬合困難,難以手算與電算,個別城市單獨統計實在不容易,且不同擬合方法也有一定差異,計算結果往往因人而異。”[4]
應該承認,在計算機軟硬件功能欠發達的年代,求解皮爾遜Ⅲ型分布的最優解存在一定難度。但是,隨著時代的進步,皮爾遜Ⅲ型分布最優解的求解方法已經成熟,因此,目前城市暴雨強度公式編制中理論頻率曲線應采用皮爾遜Ⅲ型分布曲線,而不僅僅是指數分布曲線。
3 皮爾遜Ⅲ型分布求最優解的三大問題
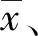
式中:n——樣本數;
xi——第i個樣本值。
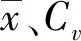
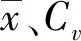
(3)如何判斷所求理論頻率分布曲線為最優,即擬合準則的選擇問題。
4 快速求解皮爾遜Ⅲ型分布曲線
針對皮爾遜Ⅲ型分布曲線累積分布函數(公式(1)),令t=β(x-a0),tp=β(xp-a0),則:
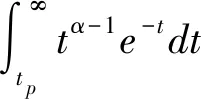
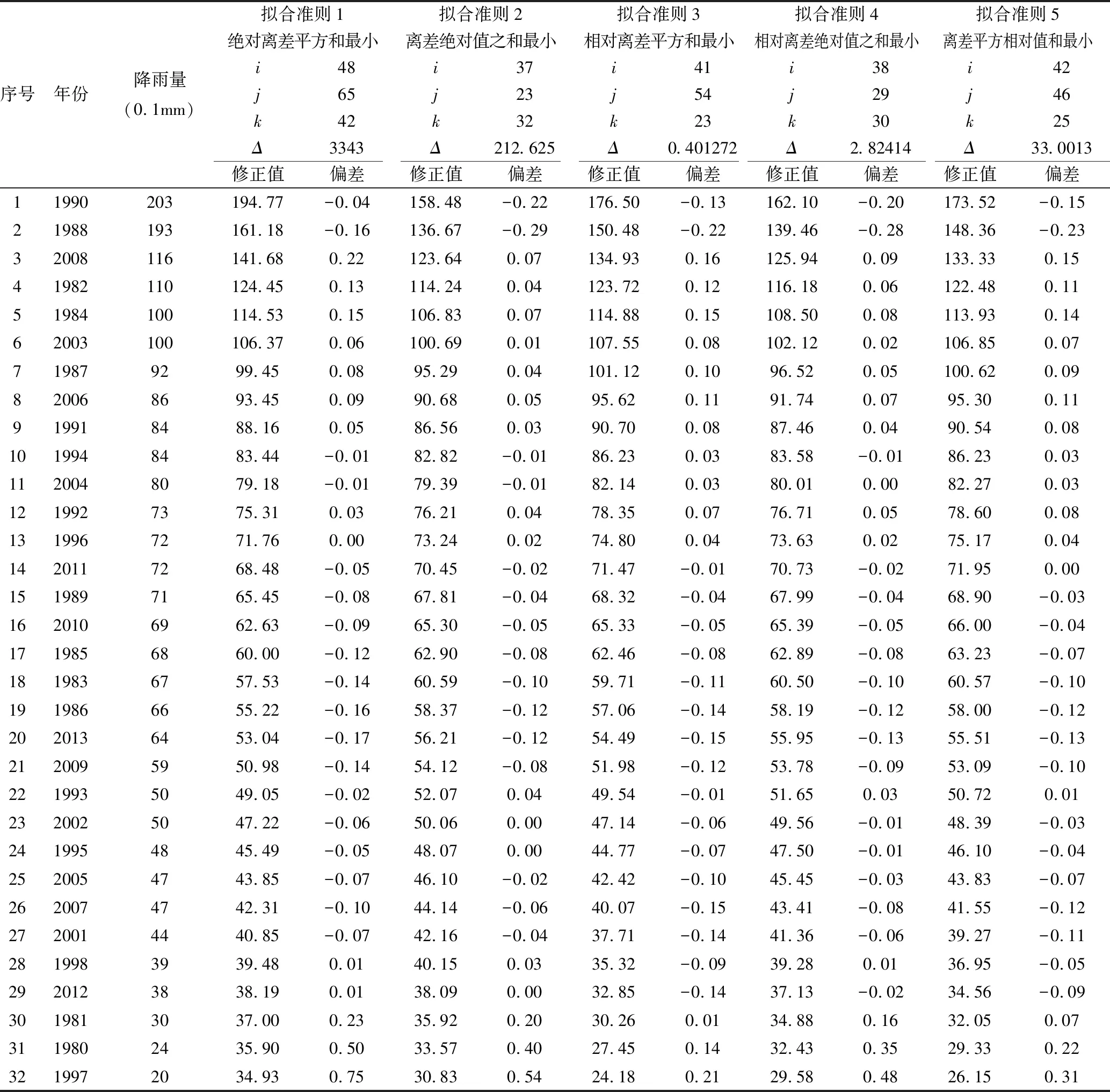
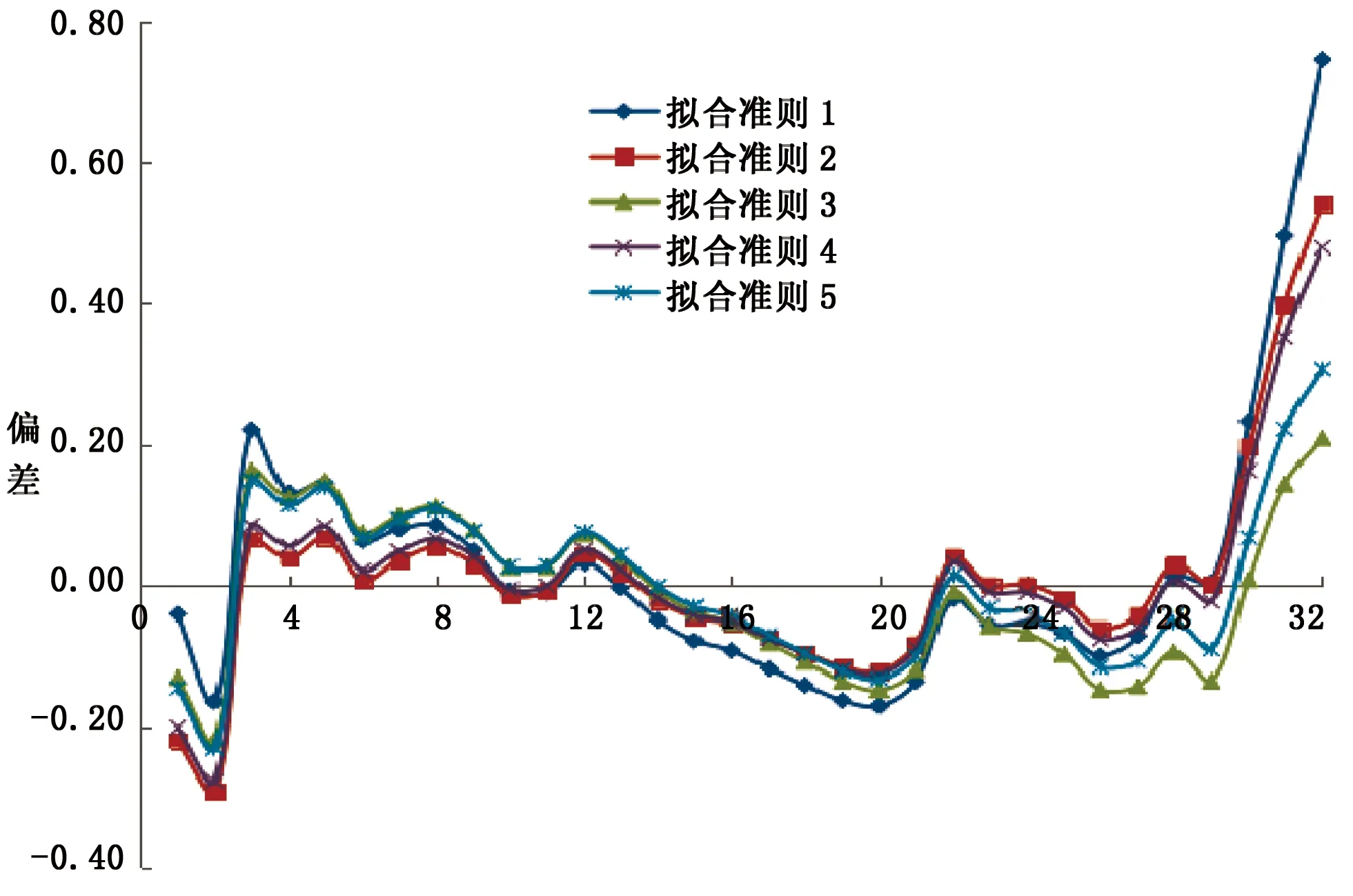
當0 當t≥α+1時,采用連分數形式展開,可以快速收斂,計算公式為[6]: 當t=0時,p(t≥tp) = 0。 該公式收斂速度較慢,使用時用戶應根據需要計算出更多的展開項。 當給定頻率Ps,可用牛頓迭代法求解對應的t值,迭代公式為[6]: s-1=1,s0=t,q-1=0,q0=1 s-1′=0,s0′=1,q-1′=0,q0′=0 當i(>0)為偶數時: 當i(>0)為奇數時: 因為級數形式和連分式形式的展開式收斂均較快,展開深度i不必太大,建議取10即可。牛頓迭代法中初值t0原則上可取任意大于0的實數,但受斯特林展開式精度的限制,不宜取太大(太大時,迭代計算將會出現數值溢出),建議初值t0取樣本t的平均值。迭代次數k由迭代精度ε控制,當給定α,若|tk+1-tk|≤ε|tk+1|,則tk+1為對應于已知設計頻率Ps的所求值t。 為判斷理論頻率分布曲線與原始數據的適合性,常采用的擬合準則有以下5種[8-9]: (1)絕對離差平方和最小 (2)離差絕對值之和最小 (3)相對離差平方和最小 (4)相對離差絕對值之和最小 (5)離差平方相對值和最小 第(1)、(2)種擬合方法,高區數據(高重現期)和低區數據(低重現期)對結果的影響不同(不等權),有可能導致低區數據偏離較大;第(3)、(4)種擬合方法,高區數據和低區數據對結果的影響相同(等權);第(5)種方法則試圖在第(1)和第(3)種方法之間尋找平衡。由于目前并不清楚自然界暴雨的準確規律(皮爾遜Ⅲ型分布只能說從統計規律上相對較好),而且原始數據的波動(最大值和最小值之比)又有大有小,所以很難說哪種擬合準則更好。 很多研究者試圖通過比較不同理論頻率分布曲線擬合誤差的大小,衡量理論頻率曲線的優劣,這種做法存在以下缺點: (1)指數分布曲線和耿貝爾分布曲線,均為皮爾遜Ⅲ型分布曲線的特例,如果把皮爾遜Ⅲ型分布曲線和它的特例比較,必須有一個前提,即保證皮爾遜Ⅲ型分布曲線為最優形式。而當皮爾遜Ⅲ型分布曲線為最優形式時,其擬合精度必然比它的特例擬合精度高,這是由皮爾遜Ⅲ型分布曲線最優解的求解方法決定的。 (2)撇開皮爾遜Ⅲ型分布曲線,其它4種分布中,即使某種分布的擬合精度更高,也不代表這種分布更優,因為從有限的資料中并不能確定自然界降雨的準確規律。 (3)假如擬合精度高的分布就是更好的分布,那么,不進行任何調整,直接采用經驗頻率曲線就應該是最好的選擇,因為此時擬合誤差為0。而前面已經分析過,直接采用經驗頻率曲線而不采用理論頻率分布曲線進行調整是不合理的。 其中,上文的5種擬合準則中的(2)式為目標函數,(3)(4)(5)式為約束條件。 Cvmin= 0.8Cv樣本,Cvmax=1.2Cv樣本 Cv樣本——樣本變差系數。 水文學研究表明,暴雨的Cs約為2.5~4.0Cv,采用計算機求解時,可放寬至1.5~5.0Cv。同時,皮爾遜Ⅲ型分布曲線要求樣本值x大于等于a0,即: 式中,xmin——樣本系列中最小的樣本值。 為了確保皮爾遜Ⅲ型分布曲線涵蓋指數分布和耿貝爾分布,Cs=2和Cs=1.1395兩種情況應包含在內,因此: Csmin=min(1.1395,1.5Cv), 式中:min和max分別表示求最大值和最小值。 皮爾遜Ⅲ型分布曲線最優解的求解最終可表示為: 上式可采用枚舉法、遺傳算法等方法求解。 應用案例采用枚舉法求解皮爾遜Ⅲ型分布曲線最優解,參數取值如下: Cv=(0.8+0.005×j)Cv樣本 Cs=min(1.1395,1.5Cv)+ 式中,i,j,k均為整數,且0≤i≤80,0≤j≤80,0≤k≤70,即總共計算465 831種組合情況,這樣的精度完全可以滿足工程計算的要求。原始數據采用表1降雨資料(5min歷時),計算結果如表4所示,擬合結果如圖2所示。 表4 皮爾遜Ⅲ型分布曲線調整結果 圖2 擬合結果比較圖 從表4和圖2可以看出: (1)高重現期時,偏差從小到大依次為:擬合準則1、擬合準則3、擬合準則5、擬合準則4、擬合準則2。 (2)低重現期時,偏差從小到大依次為:擬合準則3、擬合準則5、擬合準則4、擬合準則2、擬合準則1。 (3)當重現期為33年一遇時,修正值均比原始值20.3mm小,說明20.3mm的實際降雨重現期大于33年一遇。 (4)當重現期為1年一遇時,修正值均比原始值2.0mm大,說明2.0mm的實際降雨重現期小于1年一遇。 再次重申,在自然界降雨準確規律不確定的情況下,不同擬合準則得到的頻率分布曲線不存在優劣之分,使用時應結合其它資料判斷。在本文應用案例中,認為擬合準則3選中的可能性更大。 (1)城市暴雨強度公式編制中,降雨資料應采用理論頻率分布曲線進行修正。 (2)理論頻率曲線應選用皮爾遜Ⅲ型分布曲線,指數分布曲線和耿貝爾分布曲線均為皮爾遜Ⅲ型分布曲線的特例。 (3)只有在理論頻率分布曲線和擬合準則均相同的情況下,才能根據擬合精度高低判斷頻率分布曲線的優劣。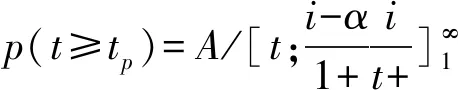
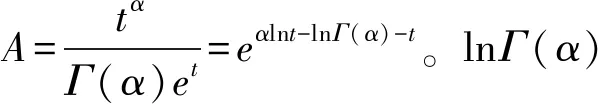
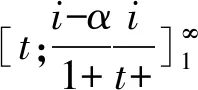
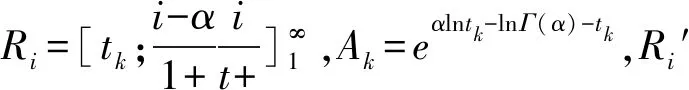
5 擬合準則
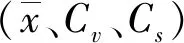
6 皮爾遜Ⅲ型分布曲線最優解
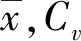
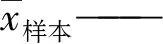
7 應用案例
8 結論

