六旋翼無人機旋翼轉動對測風準確性的影響研究

李正農, 胡昊輝沈義俊

(1.湖南大學 建筑安全與節能教育部重點實驗室, 長沙 410082；2.華南理工大學 土木與交通學院, 廣州 510641)

0 引 言

1992年，澳大利亞氣象局Greg Holland首次提出以氣象無人機攜帶皮托-靜壓管等儀器測風的方法[1-2]，其后研究者競相開展無人機搭載氣象儀器的研究和試驗。目前，國內外多采用固定翼無人機進行測風試驗，基于地速、空速、風速三者的矢量三角形關系來解算風速和風向角[3-5]，并提出了各種改進方法使解算結果更加準確[6-8]。但是，由于固定翼無人機的前飛特性，當需要在特定點進行風速、風向時程測量或飛行區間有限時(如靠近建筑物飛行)，其應用就受到了限制。

近年來，多旋翼無人機逐漸普及，與固定翼無人機相比，它具有精確懸停、垂直起降、操作簡單、成本較低等優點，在航空管制方面受限也相對較少。2015年，Neumann等[9]基于風洞試驗和現場實測，利用四旋翼無人機機載傳感器測量的有關參數，提出了擬合公式來解算風速與風向角，風速解算結果較為準確，而風向解算結果并不理想。因此，有研究者提出利用多旋翼無人機搭載額外的測風儀器直接測量風速、風向信息。該方法最主要的問題在于無人機旋翼轉動引起的擾流對測風儀器存在干擾，目前相關研究極為有限。2018年，Prudden等[10-11]將無人機與風向標結合，并將多孔風速探頭置于機頭前方4.5倍旋翼直徑處測量風場。其缺點在于：多孔風速探頭僅能測量來流，探測范圍局限于90°的錐形區域內，無法測量該區域之外的湍流；風向標的被動風向對準機制也使風向測量存在一定誤差。2014年，de Boisblanc等[12]將超聲波風速儀置于六旋翼無人機機身中心上方0.83倍旋翼直徑處進行風洞試驗，發現來流風速為0.90 m/s時，旋翼轉動引起的平均風速誤差為0.13 m/s，對于風速較大的情況及不同風向角對風場測量準確性的影響則未作研究。2016年，Bruschi等[13]在四旋翼無人機上方安裝微電子風速探頭進行風洞試驗，當來流風速小于10 m/s時，旋翼轉動對風速測量結果影響顯著，但在所測風速范圍內，旋翼轉動對風向角測量幾乎沒有影響。對于不同高度處的風場測量準確性，以及一定來流風速下無人機傾斜對風場測量結果的影響，該試驗未作研究。

本文主要針對六旋翼無人機旋翼轉動引起的下洗流場對安裝于無人機中心上方不同高度處的測風儀器測風準確性的影響開展風洞試驗，分析不同風向角及機身傾斜對風場測量準確性的影響，為無人機搭載測風儀器直接測風的實際應用提供參考。

1 試驗裝置

1.1 無人機

常見的無人機包括四旋翼、六旋翼和八旋翼無人機。綜合考慮載重量、體積、飛行穩定性、動力系統失效容忍度等因素，本文采用六旋翼無人機作為飛行平臺。該無人機對稱電機軸距為900 mm，單個機臂長358 mm，中心架直徑272 mm。整機重量4.7 kg(含電池)，最大額外載重3.5 kg；額外載重2.0 kg時，懸停時間約為20 min。

1.2 超聲波風速儀

安裝于無人機上方的測風儀器主要有以下選擇：皮托-靜壓管、熱線風速儀、傳統風杯式風速風向儀、超聲波風速儀。如以皮托-靜壓管測量風向，需在一個圓周范圍內每隔10°安裝一個(由于自然界風向不確定)，這無疑會增加結構的重量和復雜性[9]；熱線風速儀則存在無法測量風向以及積灰問題；傳統風杯式風速風向儀體積較大，在無人機上安裝還存在振動、磨損問題。因此，本文選用賽能SA210M二維超聲波風速儀進行風速、風向測量，采樣頻率1 Hz。超聲波風速儀相關參數見表1。

表1 超聲波風速儀參數Table 1 Parameters of ultrasonic anemometer

在風洞中，在不同風速下對該超聲波風速儀進行二次標定(出廠時已標定)。標定時，采用澳大利亞TFI Series100眼鏡蛇三維脈動風速探頭與該超聲波風速儀在同一高度同時進行測量，標定結果見表2。由表2可見，該超聲波風速儀與眼鏡蛇三維脈動風速探頭所測風速基本一致，準度滿足試驗要求，可用二者所測數據直接進行對比分析。

另外，為了實現風速、風向數據的實時獲取傳輸，采用小型無線電臺與風速儀進行整合。

表2 風速標定結果Table 2 Wind speed calibration results

1.3 測風整體系統

整合上述試驗裝置，得到無人機測風整體系統，整機重量為6.0 kg。對其作可行性檢驗，在室外進行試飛測試，無人機可正常懸停，且能實時在電腦端接收到風速、風向時程信號。

2 試驗設計

試驗在湖南大學HD-3低速直流邊界層風洞中進行。該風洞氣動輪廓全長14 m，試驗段全長12 m，截面尺寸3.0 m×2.5 m，轉盤直徑2 m。試驗段風速0～20 m/s連續可調。一般根據模型縮尺比在試驗段前端布置尖劈和粗糙元實現湍流度調整，使風剖面滿足規范規定；空風洞時，流場為均勻流。

由于風洞中GPS信號較弱，無人機無法在GPS模式下精確懸停；在姿態模式下又會出現隨風漂移現象，對操作要求高，極易發生碰撞。因此，為盡量減小地面效應影響，試驗中將無人機固定于高1 m的支架上，且各工況均滿足阻塞率相關要求。同時，采用手動模式，在每個工況下都將遙控器油門推到固定值，保持無人機旋翼轉速恒定。

試驗所用無人機為足尺模型，受風洞尺寸限制，無法模擬實際足尺流場。一般來說，采用縮尺比構造的流場在1 m高度處的湍流度較小，但在實際情況下，無人機所處流場不可能完全均勻，故仍在試驗段前端布置了一定的尖劈和粗糙元，如圖1所示。

圖1 尖劈和粗糙元布置圖

2.1 旋翼轉速標定

試驗采用直徑為38.1 cm的螺旋槳，螺距為13.2 cm。根據旋翼所受升力與轉速之間的關系曲線[14-15]，同時考慮試驗所用無人機機臂存在一個向上8°的傾角以及旋翼間的相互干擾效應，估算出無風狀態下無人機懸停時的旋翼轉速約為5000 r/min(不考慮風速及機身傾斜等因素對轉速的影響)。

為標定旋翼轉速達到5000 r/min時的油門值，以非接觸光電式轉速儀發射光線至粘貼于螺旋槳上的熒光片獲得反射信號來測量轉速。在不同風洞控制風速vc下(vc為4、6、8和10 m/s)標定旋翼轉速，結果顯示：當油門值一定時，旋翼轉速穩定在(5000±100) r/min。

2.2 工況設計

首先，需要研究旋翼轉動對安裝于無人機上方不同高度處的超聲波風速儀測風準確性的影響。為在減小湍流作用的同時不影響無人機的飛行穩定性，制作了6個不同高度的風速儀安裝支架(編號1～6)，使風速儀探頭距離無人機上部中心板分別為0.53、0.79、1.05、1.31、1.57和1.84倍旋翼直徑。

其次，需要研究來流從不同角度入射對風場測量準確性的影響。考慮到六旋翼無人機的對稱性以及無人機槳葉的正反槳之分(為了防止自旋)，通過轉動風洞底部轉盤，選取風向角β為0°、30°和-30°進行研究。當風向角β=30°時，正對來流的旋翼為反槳(順時針旋轉)；當風向角β=-30°時，正對來流的旋翼為正槳(逆時針旋轉)。試驗布置及風向角設定如圖2所示。

(a) 試驗布置

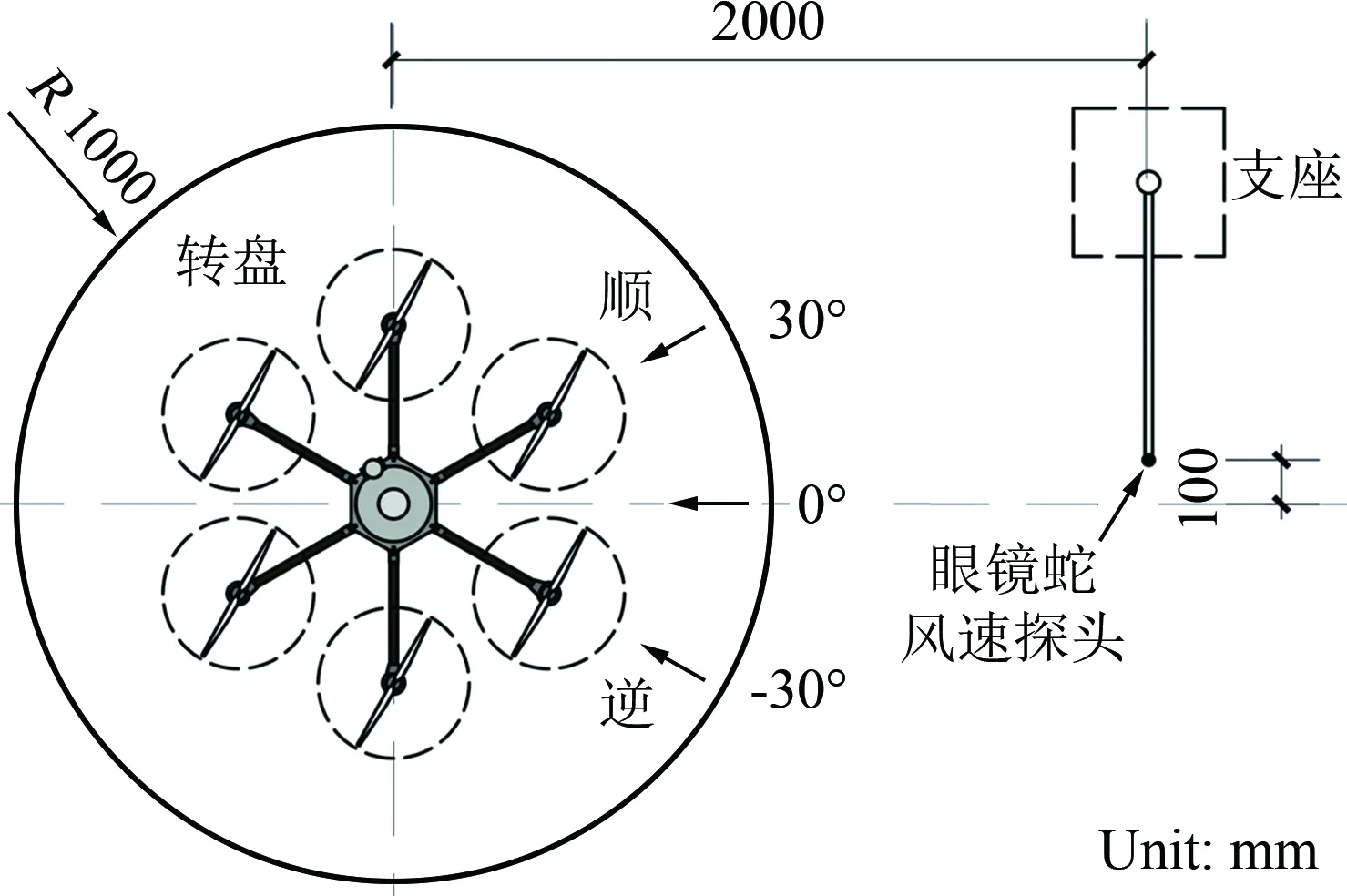
(b) 風向角設定

當來流風速不為0時，為保持無人機定點穩定懸停，機身會存在一定傾斜。因此，試驗還考慮了機身傾斜對風場測量結果的影響。根據無人機懸停時所受風阻力FZ與重力W之間的關系(如圖3所示)，由式(1)和(2)可大致估算出無人機在不同來流風速v下的傾斜角度α。

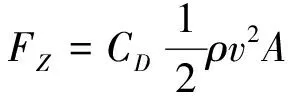
(1)

(2)

式中，CD為無人機整機阻力系數(近似取1，根據無人機廠家提供的最大飛行速度和最大傾角計算得到)，ρ為空氣密度。A近似取機身水平時的無人機迎風面積，通過拍照并由Photoshop顯示的像素數(相當于照片中的面積大小)及式(3)計算得到(風速儀迎風面積由廠家提供的圖紙得到)。

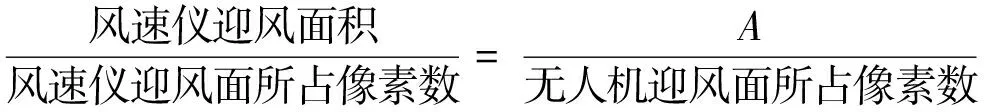
(3)

根據計算結果，當控制風速vc為8 m/s時，取α為5°；當vc為10 m/s時，取α為10°；當vc為4和6 m/s 時，α的計算結果均小于3°，不作機身傾斜分析。

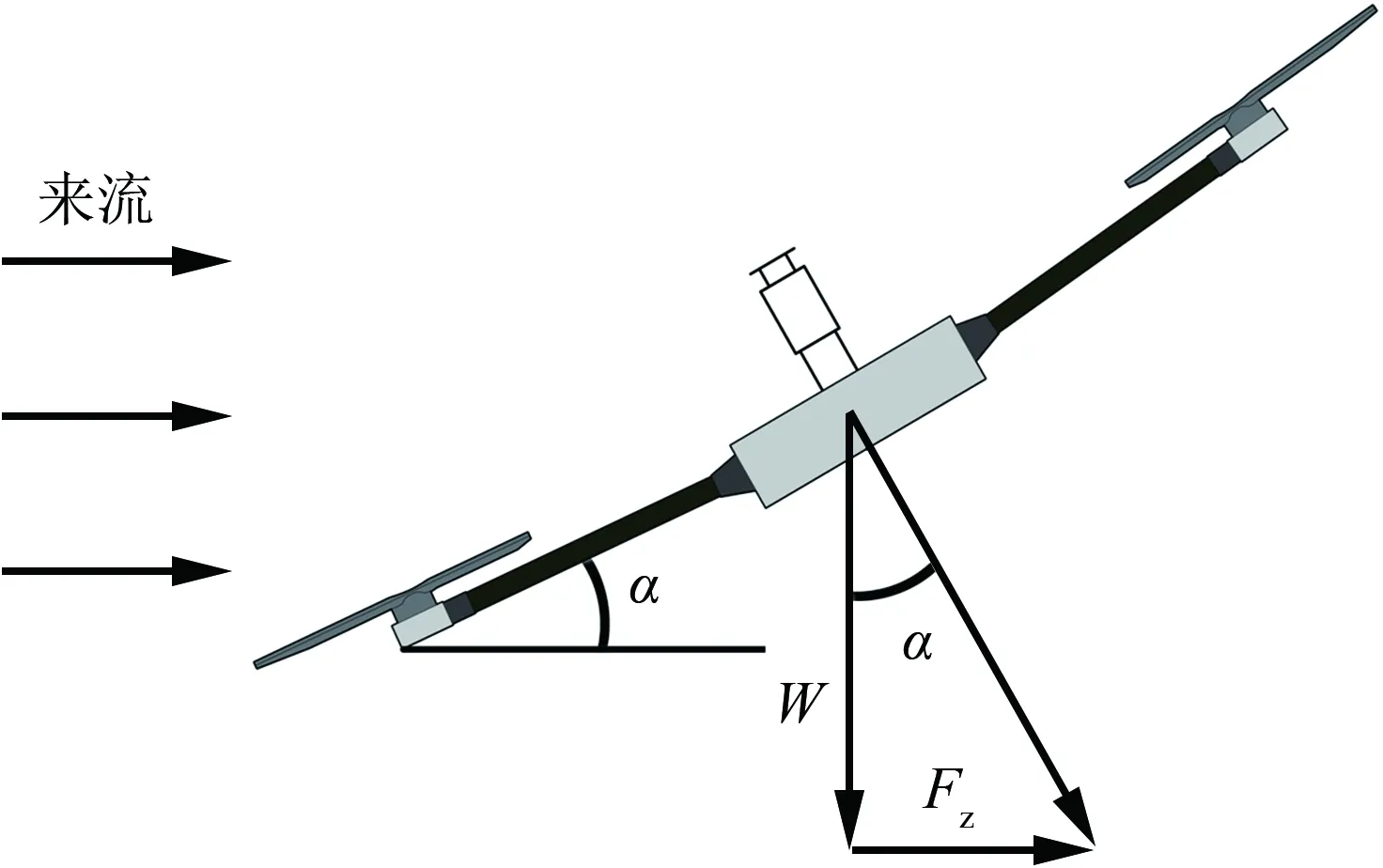
圖3 機身傾斜角計算示意圖

試驗時，將眼鏡蛇風速探頭置于超聲波風速儀前方測量風速。在風洞控制風速vc為4、6、8和10 m/s條件下(控制風速測定點位于試驗段前端上部，來流經過尖劈和粗糙元后，風速會略有減小)，考察旋翼轉動對風場測量準確性的影響，每組數據測量時間為2 min。

經驗證，眼鏡蛇風速探頭置于超聲波風速儀的各安裝高度時，各工況下旋翼轉動對測得風速的影響最大只有0.18 m/s(大多在0.10 m/s以內)，基本可以忽略，因此其測得的風速均值可作為參考來流風速。

3 結果分析

3.1 機身水平且旋翼靜止時對風速測量的影響

圖4給出了無人機機身水平且旋翼靜止時，各工況下超聲波風速儀與眼鏡蛇風速探頭測得風速之間的相對誤差曲線(相對于眼鏡蛇風速探頭測得的數據)。需要說明的是，不同高度處超聲波風速儀的數據對應于相同高度處眼鏡蛇風速探頭的數據(后同)。

由圖4可見，在不同工況下，來流經過試驗裝置引起的風速相對誤差隨高度的變化趨勢基本相同。當采用1號支架時，由于無人機機臂及旋翼的阻擋，來流經過無人機后，風速會略微減小；當采用2～4號支架時，風速則略微增大，這是由于無人機的阻擋改變了氣流流向，使其往稍高處通過，導致此高度范圍內流速增大；當采用5～6號支架時，風速基本不變，誤差保持在±1%以內。

控制風速vc為6、8和10 m/s時，相對誤差基本在±2%之內，可認為在這3個控制風速下，來流風速經過無人機后不受影響。當控制風速為4 m/s且采用2～4號支架時，經過無人機后風速有一定程度增大，相對誤差最大為4.39%，但仍小于5%，且絕對誤差只有0.16 m/s，與該工況下旋翼轉動引起的絕對誤差相比仍可以忽略，故后文主要分析旋翼靜止與轉動時超聲波風速儀測得風場的變化情況。

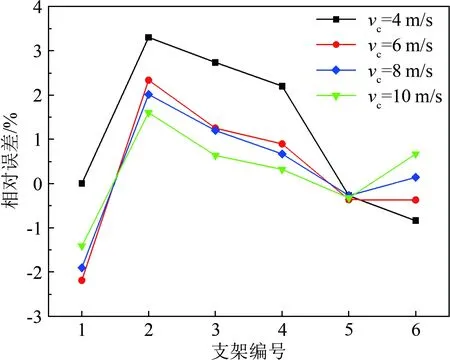
(a) 風向角β=0°

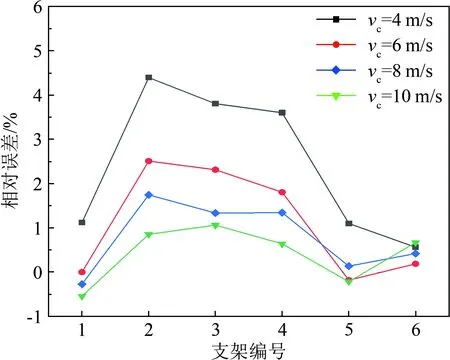
(b) 風向角β=30°

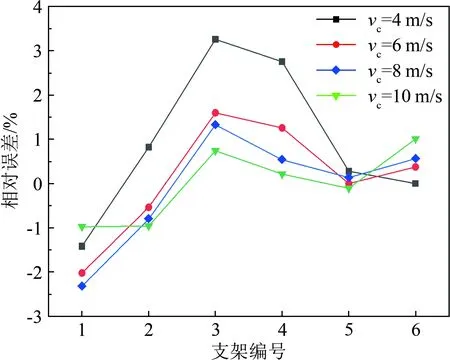
(c) 風向角β=-30°

Fig.4Curvesofrelativewindspeederrorundervariousconditionswhenrotorsarestationary

3.2 機身水平時旋翼轉動對風速測量的影響

表3給出了各工況下旋翼轉動引起的計算湍流度變化情況(由超聲波風速儀測得的風速時程計算得到。需要指出的是，該計算湍流度是基于湍流強度計算公式對來流脈動的大體評估)。試驗中測得的來流湍流度(由眼鏡蛇風速探頭測得，采樣頻率500 Hz)均小于5%。由表3可見，計算湍流度最大增幅1.64%，發生在1號支架及風向角0°、控制風速10 m/s的工況下；其他工況的計算湍流度變化均在±1%之內，且在絕大多數工況下還有略微減小，這表明在該時間尺

度上旋翼轉動對來流脈動影響不大。由于本測風系統主要用于氣象測量，更關注平均風速和陣風特性，因此后文主要對旋翼轉動對來流平均風速的影響展開分析。圖5和表4分別給出了機身水平時各個工況下旋翼轉動引起的風速相對誤差曲線和風速絕對誤差。

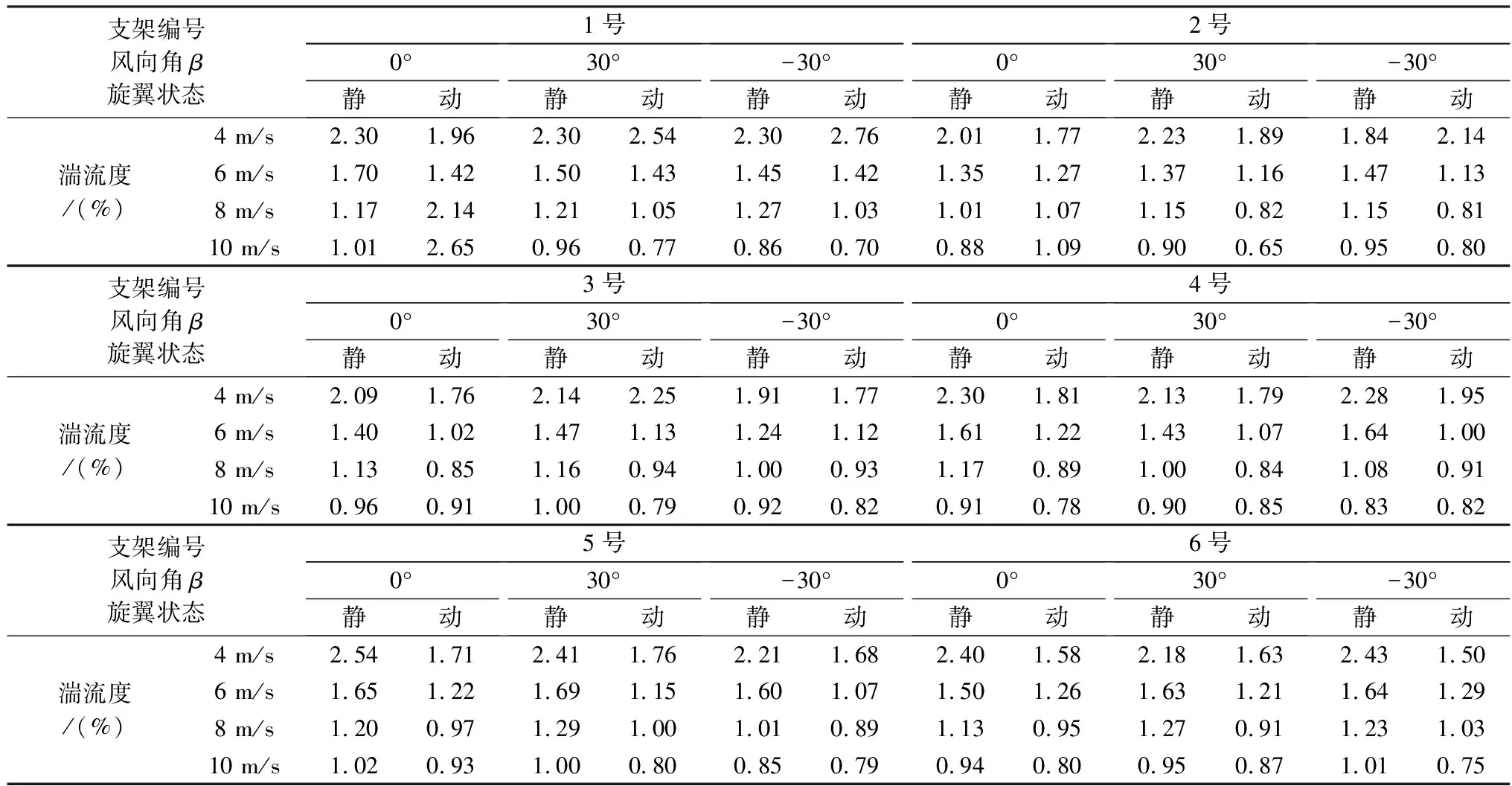
表3 各工況下旋翼轉動引起的計算湍流度變化Table 3 The change of calculated turbulent intensity caused by rotors rotation under various conditions

(a) 風向角β=0°

(b) 風向角β=±30°

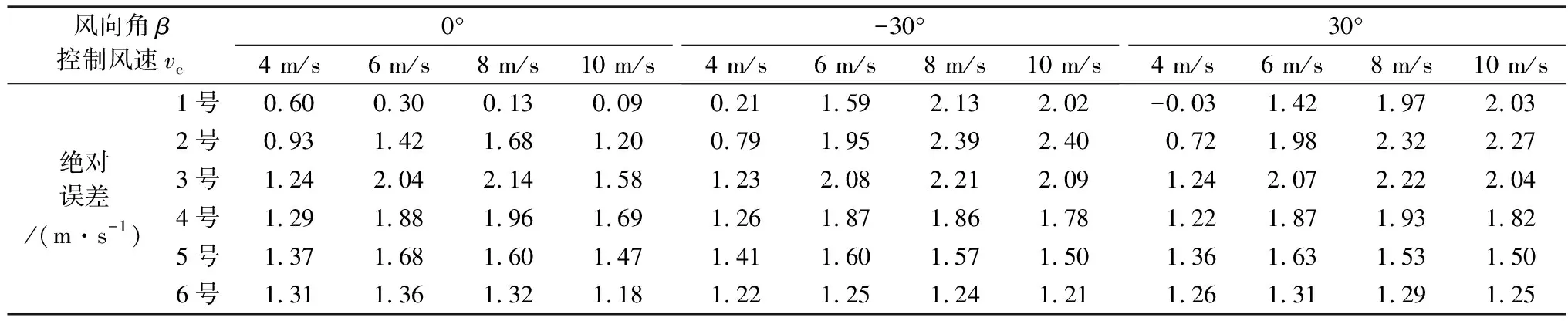
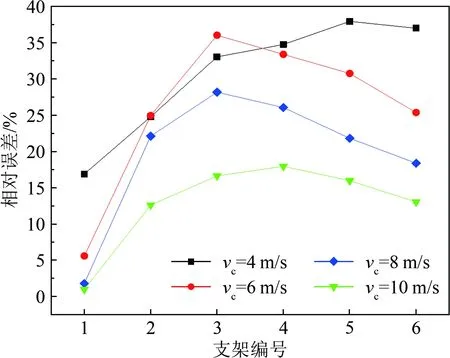
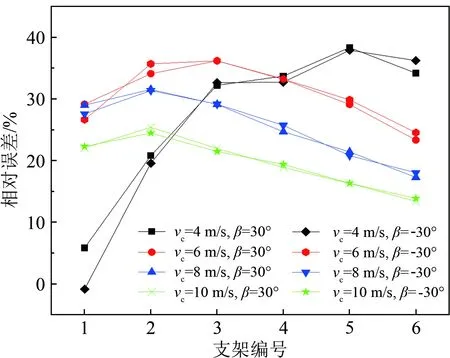
圖5 各工況下旋翼轉動引起的風速相對誤差曲線

3.2.1 風向角0°時旋翼轉動對風速測量的影響

由圖5(a)可見，風向角β=0°時，總體上，旋翼轉動引起的風速相對誤差隨風速儀安裝高度均呈先增大后減小的趨勢。當控制風速為4 m/s時，風速相對誤差隨高度的變化趨勢與其他3個控制風速下明顯不同，表現為采用5號支架時相對誤差達到最大。當控制風速為6、8和10 m/s時，風速相對誤差的變化趨勢大體相同，且在相同的風速儀安裝高度下，呈現出隨控制風速增大而減小的特點。

由表4和圖5(a)可見，當采用1號支架時，各控制風速下旋翼轉動引起的風速絕對誤差均不大，且隨控制風速的增大而減小。其中，當控制風速為8和10 m/s時，相對誤差均小于5%。當采用2號支架且控制風速為6、8和10 m/s時，旋翼轉動引起的風速相對誤差較1號支架均大幅增加(其中，控制風速為6和8 m/s時，相對誤差增幅超過20%；控制風速為10 m/s時，誤差增幅相對較小)。另外，當采用2～4號支架時，風速絕對誤差隨控制風速也呈先增大后減小的趨勢，并在控制風速為8 m/s時達到最大，與文獻[13]給出的結果一致。當采用5～6號支架時，風速絕對誤差隨控制風速的變化趨勢稍有不同，在控制風速為6 m/s時達到最大。

3.2.2 風向角±30°時旋翼轉動對風速測量的影響

-30°和30°風向角分別代表正反槳正對來流的情況。由圖5(b)可見，風向角β=±30°時，旋翼轉動引起的風速誤差在各相應工況下基本相同，并沒有因為正反槳的差別導致流場的不對稱。

當風向角β=±30°時，風速相對誤差的總體規律與風向角為0°時基本一致；當控制風速為10 m/s時，其風速誤差始終較大，這與文獻[13]中四旋翼無人機的風洞試驗結果有所差異。由文獻[16]可知，六旋翼無人機中心位置處流場變化的主要原因是無人機后部旋翼對氣流的影響。當風向角為±30°時，六旋翼無人機有3個旋翼位于風速儀后方，而四旋翼無人機在風向角為45°時只有1個旋翼位于風速儀后方，前者對氣流的加速作用要大得多。此外，雖然試驗中風洞控制風速達到了10 m/s，但由于尖劈和粗糙元的作用，實際來流風速并未達到文獻[13]中指出的10 m/s這一臨界風速，試驗結果的差異也與此有一定關系。再者，控制風速為6、8和10 m/s時，風速相對誤差隨控制風速的增大而減小，說明確實存在“當風速大于一定值時，風速越大，旋翼轉動對風速測量準確性影響越小”這一規律，也從另一方面說明了本文結果的可靠性。

但總體而言，風向角的變化并不會引起各工況下風速誤差總體規律的改變：

(1) 在0°風向角下，使用1號支架且風速為6、8和10 m/s時，旋翼轉動引起的風速相對誤差較小(小于5%)，其余支架情況下，尤其是在低風速的情況下，風速相對誤差均較大。

(2) 隨著高度的增加，風速誤差均呈現先增大后減小的趨勢。文獻[16]指出，無人機旋翼轉動時，氣流在機身中心附近改變方向向上流動(文獻[11]使用煙線儀測量流場時也出現了類似現象)，繼而受到旋翼影響向下分流，使無人機上部靠近旋翼平面處存在一個相對靜風區，該區域隨著旋翼間距比(相鄰兩旋翼中心距離L與旋翼直徑D之比)的增大和動力源(旋翼數)的增多而增大，其上方風速增大。該結果可以較好地解釋本文試驗現象。

(3) 在風速儀安裝高度低于1.31倍旋翼直徑(使用1～4號支架)且控制風速為6、8和10 m/s的情況下，風向角為±30°時，旋翼轉動引起的風速誤差基本上都大于風向角為0°時相應工況下的風速誤差，而控制風速為4 m/s時則情況相反。

(4) 由表4可見，隨著風速儀安裝高度的增加，當采用6號支架時，各個工況下的風速絕對誤差趨于一致，表明來流風向角和速度大小對風速絕對誤差差異性的影響減弱，且控制風速越小，不同風向角下的風速絕對誤差隨高度能更快地趨于一致。

3.3 機身水平時旋翼轉動對風向測量的影響

圖6給出了機身水平時各工況下超聲波風速儀測得的風向角。在各工況下，旋翼轉動對風向角的測量并不會產生較大影響，其最大誤差為2.61°，小于4°，在超聲波風速儀的誤差范圍之內。需要說明的是，

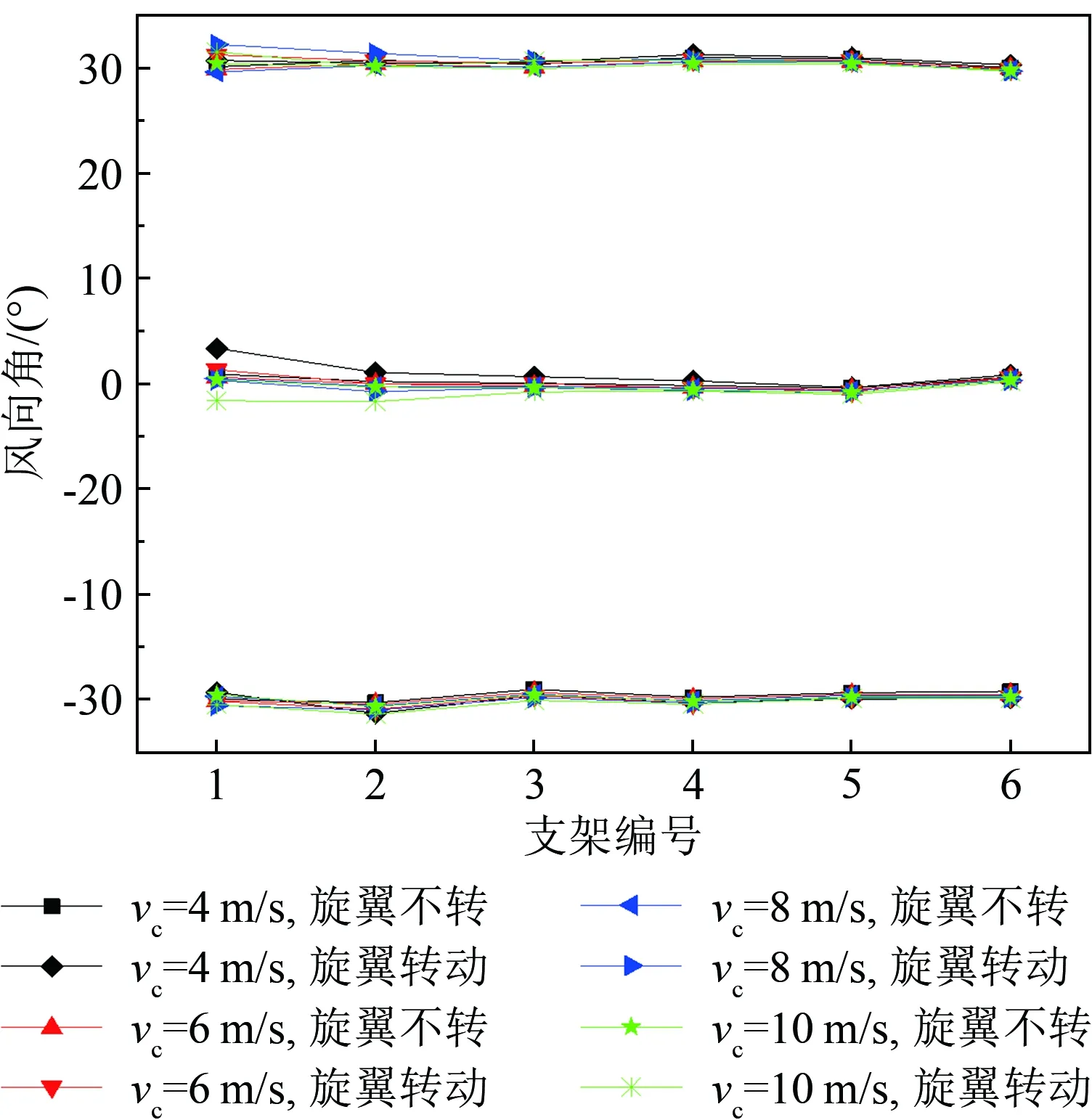
圖6 各工況下測得的風向角

為保持坐標軸及全文討論的一致，對-30°工況下的角度原始數據作了減去360°的處理(后文同)。

3.4 機身傾斜對風場測量結果的影響

試驗發現，當無人機機身傾斜且旋翼靜止時，各個工況下超聲波風速儀測得的風速都比眼鏡蛇風速探頭測得的有所增大，增大程度隨著傾斜角度的增大而增加。當控制風速為8 m/s時，機身傾斜角度為5°，風速相對誤差雖有所增大，但均小于5%(3%左右)，仍可以接受；當控制風速為10 m/s時，機身傾斜角度為10°，風速相對誤差基本上都大于5%(6%左右)。這主要是由于試驗采用的二維超聲波風速儀的探頭上方有一用于反射超聲波的蓋板，當無人機傾斜時，蓋板與探頭之間的區域迎風面積減小，對氣流起到了加速作用(類似于峽谷效應)。

3.4.1 機身傾斜對風速測量結果的影響

圖7為旋翼轉動、機身水平和傾斜時的風速相對誤差曲線。從圖中可見，機身傾斜時，旋翼轉動引起的風速相對誤差總體規律基本未變，隨著風速儀安裝高度的增大，依舊呈現出先增加后減小的趨勢。

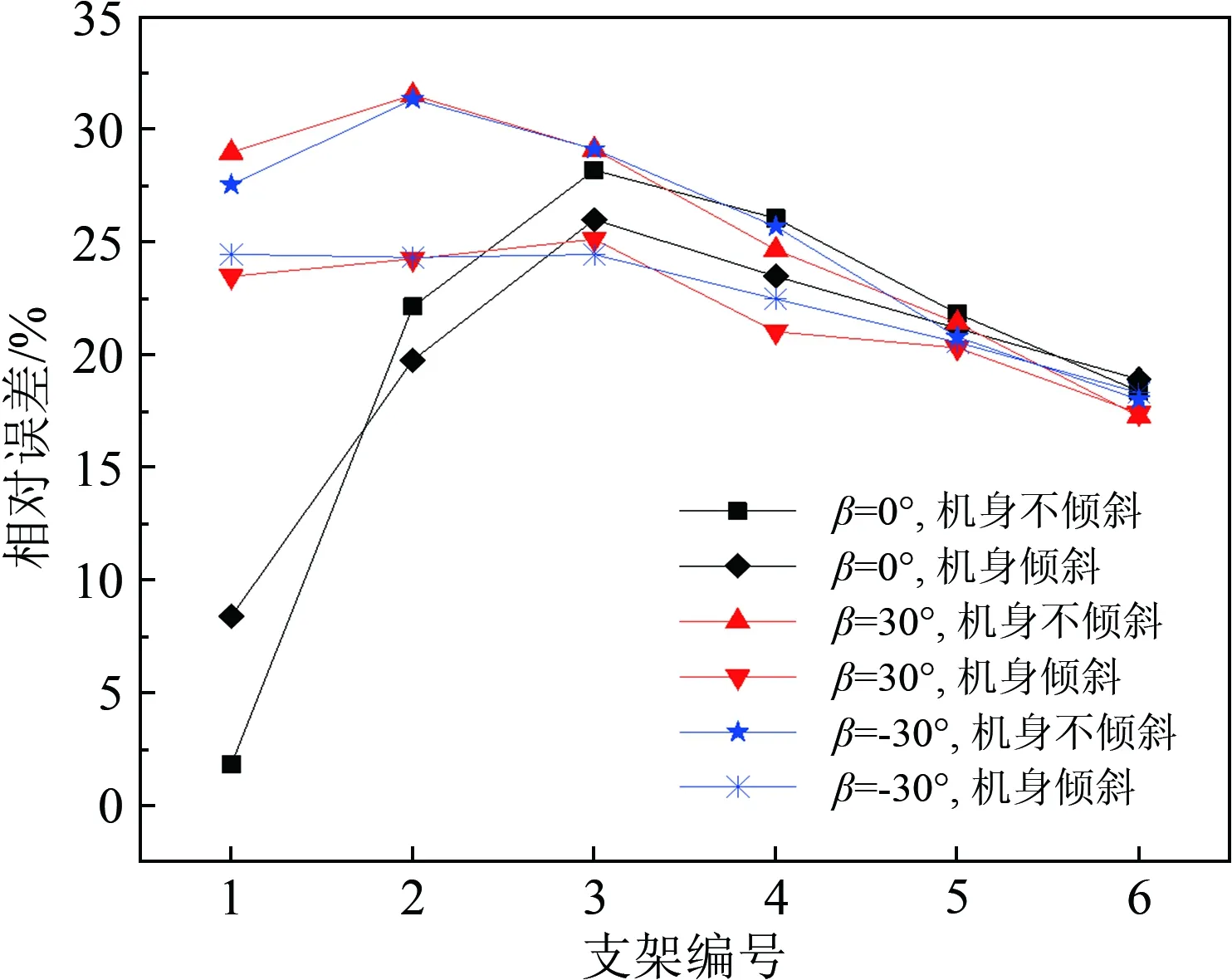
(a) 控制風速vc=8 m/s

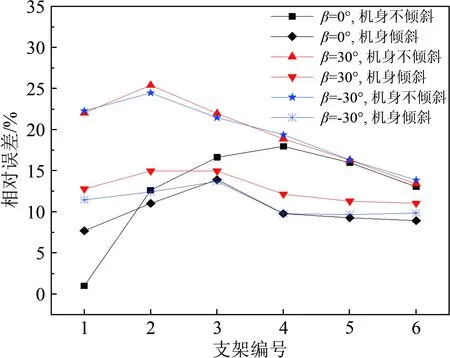
(b) 控制風速vc=10 m/s

Fig.7Comparisonofrelativewindspeederrorbetweentiltedfuselageandhorizontalfuselage

當風向角為0°、旋翼轉動且采用1號支架時，機身傾斜時的風速誤差較機身水平時有所增大：控制風速為8 m/s時，其絕對誤差為0.63 m/s，相對誤差為8.39%；控制風速為10 m/s時，其絕對誤差0.75 m/s，相對誤差為7.68%，但都控制在10%之內。

機身傾斜時的其他工況，風速誤差都比機身水平時的對應工況小，表明機身傾斜對風場測量的準確性會有一定的提高作用。另外，從圖7(a)可見，當控制風速為8 m/s時，由于傾斜角度較小，在風速儀安裝高度達到1.57倍旋翼直徑之后(5、6號支架)，旋翼轉動引起的風速相對誤差與機身水平時基本一致，表明機身傾斜對較低高度處的風場影響較大。

3.4.2 機身傾斜對風向測量結果的影響

圖8給出了機身傾斜后超聲波風速儀測得的各個工況下的風向角。可以看出，機身傾斜對風向角的測量沒有太大影響，最大角度誤差為2.34°，小于4°，在可接受范圍之內。

圖8 機身傾斜時各工況下測得的風向角

Fig.8Measuredangledataundervariousconditionswhentiltingthefuselage

4 結 論

本文針對目前利用多旋翼無人機搭載測風儀器直接測風的方法，著重研究了無人機旋翼轉動產生的下洗流場對測風準確度的影響。主要結論如下：

(1) 旋翼靜止時，試驗裝置本身對來流的影響很小。

(2) 隨著風速儀安裝高度增大，旋翼轉動引起的風速誤差呈先增大后減小的趨勢。其中，在風速儀安裝高度為0.53倍旋翼直徑且風向角為0°的工況下，當機身水平且控制風速為6、8和10 m/s時，風速誤差最小(均小于5%)；當機身傾斜且控制風速為8和10 m/s時，風速誤差較機身水平時有所增大，但仍控制在10%之內。其余工況，尤其是低風速時，旋翼轉動引起的風速相對誤差均較大(超過10%)。

(3) 當控制風速為6、8和10 m/s且風速儀安裝高度較低時，±30°風向角下旋翼轉動引起的風場測量誤差較0°風向角時大，當控制風速為4 m/s時則相反。

(4) 當機身水平時，隨著風速儀安裝高度的增大，各工況下的風速絕對誤差趨于一致，來流風向角和速度大小引起的風速誤差差異性減小，且控制風速越小，不同風向角下的風速絕對誤差隨高度增大能更快地趨于一致；控制風速為6、8和10 m/s時，旋翼轉動引起的風速相對誤差隨控制風速的增大而減小。

(5) 機身傾斜、風速儀安裝高度為0.53倍旋翼直徑時，旋翼轉動引起的風速相對誤差較機身水平時有所增大，其余高度下的風速相對誤差均較機身水平時小。

(6) 各工況下，旋翼轉動對風向角的測量幾乎沒有影響。

利用多旋翼無人機平臺搭載風速儀進行風場測量是一種新穎的方法，但還存在一定的測量誤差。后續將進行實地測量，與測風塔數據進行對比，改進測量方法，修正測量結果，增強其實用性。