類比推理在高中數學核心素養生成中的應用

江蘇省啟東中學 楊紅生

眾所周知，類比推理是銜接數學各知識點的有效方法，它能夠幫助學生理解和運用數學公式，能夠幫助學生在最短的時間內找到解題的正確思路，從而促進學生的數學能力。為了提升學生的學習能力，提高教師的教學效果，教師必須要在實際數學教學中應用類比推理教學法。

一、演算教學的類比推理

演算是數學中的重要內容，也是學生必須要掌握的基礎技能。由于數學學科的特性，它需要學生具備較強的邏輯推理能力、動手計算能力以及良好的解題反思能力。如果學生很好地記憶和理解這些公式，就容易找到解題思路。基于此，教師必須要在學習演算中，類比推理數學知識。

首先，教師應將有關聯性的數學公式列出來，學助生進行邏輯推理，從而加深學生對相關公式的記憶。例如，教師在教“三角函數”時，可以將cos、sin 的性質講述給學生，然后讓學生依據掌握的知識點去推理tan 的計算公式，從而掌握其定義域和值域。

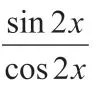
再次，教師應根據學生的接受能力，給學生列舉更多的解題方法，拓展學生的學習思維，從而使學生能夠更好地面對數學題。例如，教師在教數列時，應將前n 項和的計算方法進行歸納，通過在黑板上給學生例舉一些錯位相加、錯位相減、裂項等方法，幫助學生解決數列通項公式和前n 項和的難題。

最后，教師應不斷給學生陳列一些新穎的數學推理公式。例如，教師在教不等式時，可以依據a2+b2≥2ab 等公式，幫助學生明確公式的使用方法，從而使學生能夠利用這些公式解決不等式難題。

二、解題過程的類比推理

解題過程的類比推理主要體現在一題多解和相似的類型題上。一直以來，學生學習數學之所以很困難，主要是因為學生沒有掌握正確的學習方法。所謂正確的學習方法，就是學生利用數學現象、數學內涵、邏輯思維等要素快速找到解題思路，循序漸進地解決相應的問題。

首先，教師應全面分析和研究數學教材，將相關的數學知識進行總結，以板書的形式豐富學生的知識結構體系。例如，教師在教集合時，通過講解集合的概念和性質，給學生例舉集合的注意事項，讓學生能夠依據集合知識準確處理集合難題。為了提高學生的數學能力，教師還應在復習時給學生拓展更多的知識元素，從而提升學生的數學綜合素養。

其次，教師應注重培養學生的邏輯推理能力，全面提升學生的數學思維意識。例如，教師在教三角函數二倍角公式時，可以讓學生根據已學的公式進行更深層次的推理，從而使學生能夠牢記三角函數的各個公式。眾所周知，數學是一門邏輯性強的學科，學生掌握了二倍角公式，自然也就掌握了半倍角公式。

最后，教師應重視開發學生的類比推理思維，使學生能夠在面臨數學難題時，找到正確的解題方法。類比推理暗藏于數學公式之中，只要學生能夠掌握公式的使用條件和方法，就能從大量的數學習題中吸取經驗，從而提升自身的數學解題水平。

可見，學習數學不是一蹴而就的，它需要教師在解題過程中不斷給學生滲透類比推理思想，讓學生能夠找到各個知識點的關聯性。通過將所學知識要點進行總結，不斷掌握解題的方式和方法，讓學生能夠依據推理，實現快速、準確地解題，從而提升學生的數學能力。

三、總結歸納的類比推理

從某種角度上看，數學學習具有一定的模仿性。教師通過在黑板上給學生演練計算例題的方法，讓學生自行解決同類型題，這一直是學生獲取數學思維和能力的主要途徑。但由于教師沒有利用類比的方式，給學生講述各知識之間的關系，致使學生出現了“丟西瓜，撿芝麻”的情況。

首先，教師應做好相應的備課工作。例如，教師在教數列時，可以針對第二節的等差數列進行知識內容延伸，幫助學生掌握各種等差數列的類型題，把等差數列知識體系完整地呈現給學生，讓學生通過類比推理思考解題的方式方法，從而使學生建立學習信心，從容應對等差數列的內容。

其次，教師在實際教學中，應注重增添趣味性元素。為了更好地激發學生的智力，教師可以從網上搜尋一些新、奇、怪的習題，對學生進行相應的知識拓展。例如，教師在教數列時，可以針對第三節的等比數列內容進行習題演練，從而使學生能夠準確找到通項公式與前n 項和的關系，進而解決等比數列的難題。

再次，教師應通過對學生進行階段性的提問，測評學生的學習情況。通過掌握學生的學習情況，對學生進行更加細致的類比總結。例如，教師在教學導數時，應根據學生做題的數量，以及遇到的經典類型題，進行全面性、細致性的概括與總結。通過幫助學生構建導數解題思維，幫助學生掌握多重導數的用法及意義。

最后，教師應在實際類比推理教學中，幫助學生解決一些切入點較偏、知識關聯性強、信息隱藏性高的數學難題。例如，教師在教立體幾何時，一定要讓學生歸納和總結四邊形、三角形等平面圖形的性質與特點，通過給學生搭建一個立體思維體系，幫助學生找到點、線、面的關系，從而解決立體幾何難題。

綜上所述，數學是一門邏輯性較強的基礎素質學科，為了提高學生的數學素養和能力，教師必須要重視利用類比推理教學法。通過給學生提供更多的習題，不斷訓練學生的思維能力。通過讓學生經常進行總結與歸納，掌握處理數學習題的方式和方法，全面開發學生的數學智慧。