基于多性能指標的輕木-混凝土混合結構層間隔震

王雪亮，王秀鑫，魏凱睿，徐乾罡

(1. 武漢理工大學道路橋梁與結構工程湖北省重點實驗室，湖北武漢 430070；2. 武漢理工大學土木工程與建筑學院，湖北武漢 430070)

0 引 言

輕型木結構由于輕質高強、施工簡便、抗震性能好、綠色環保等優點而越來越受到人們的青睞。輕木結構主要應用于3層及3層以下的住宅建筑，在推廣中受到很大限制，因此出現了與其他材料結構組合而成的木混合結構。將輕型木結構“上嫁”于低層混凝土結構的木-混凝土混合結構為主要結構形式之一，已經在國內外開始應用，如倫敦的Stadthaus公寓為底部一層鋼筋混凝土結構、上部8層正交膠合木(CLT)結構的混合結構；墨爾本的Forte建筑為首層商用混凝土結構、上部9層輕木結構住宅[1]；成都青白江小學為底部1層混凝土、上部2層木結構的教學樓。這種結構形式兼具2種結構的優點，既可提供底部混凝土框架大空間，又能達到綠色環保的目的，具有較大的工程應用空間。

由于木材與鋼筋混凝土剛度懸殊，其上部木結構的地震反應相比純木結構有明顯的放大。日本的Isoda等[2]研究了底層混凝土、上部不同層數輕木結構的抗震性能，發現上部結構的剛度和質量對地震力有明顯影響。熊海貝等[3-6]對該混合結構進行了系統的理論分析、有限元模擬及地震模擬振動臺試驗研究，結果表明：上下剛度比對結構反應有非常明顯的影響，上部木結構的位移響應遠大于下部混凝土結構，其頂層加速度放大系數最大可達6，而且破壞主要發生在輕木結構的首層，明顯大于同等條件下的純木結構。

針對這一問題，何敏娟等[7]基于傳統抗震設計理論，建立了輕木-混凝土上下混合結構的抗震設計方法。在強震區，采用這種傳統抗震方法仍然無法避免上部結構的損壞，且不太經濟。據此譚柱[8]借鑒斗拱的構造及耗能機理，設計了一種新型木制隔震裝置。本文基于該裝置的試驗研究結果，將其應用于上木下混結構形成層間隔震體系，并對其進行了層間隔震效果分析。為獲得最優隔震效果，采用層間隔震體系的三質點動力模型對其進行了多性能指標的參數優化設計，確定木制隔震層的最優參數區間。

1 木制隔震裝置耗能機理

新型木制隔震裝置是一種多級復合隔震裝置，采用原木或工程木制作，無需金屬連接件，由櫨斗、泥道拱、華拱、散斗等多層短木部件交錯疊置，層層鎖扣，利用木材接觸面的摩擦滑移、木材剪切、彎曲及擠壓等非線性變形耗散能量，達到層間隔震的目的。該裝置傳承古建筑斗拱的構造特點，如圖1所示，置于建筑的中間樓層，上部承接輕木結構的地梁板，底部與混凝土結構的頂部相連接，既能美觀建筑立面，又能起到明顯的層間隔震作用，具有較強的工程應用價值。

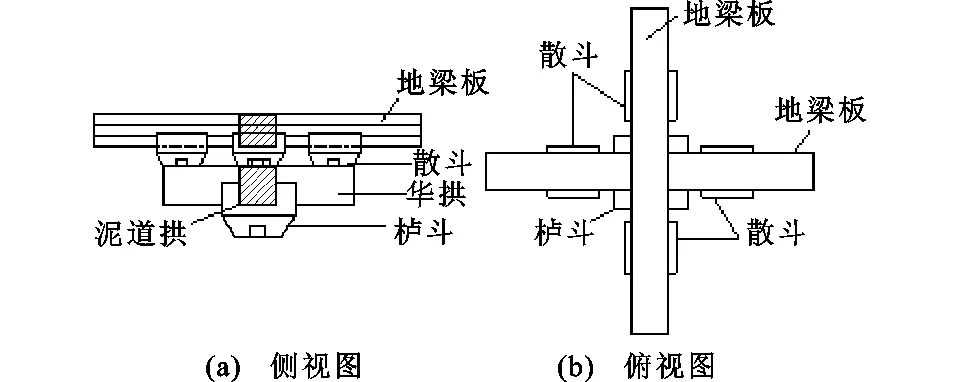
圖1 木制隔震裝置構造Fig.1 Structure of Wooden Isolation Device

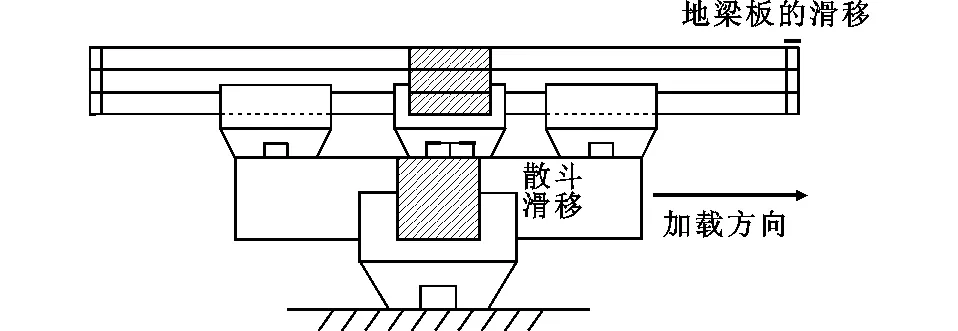
圖2 隔震裝置滑移Fig.2 Sliding of Isolation Device

新型木制隔震裝置的滑移主要發生在地梁板及散斗、散斗與拱之間，其耗能機理不同于傳統斗拱[9]。傳統斗拱榫卯之間聯系緊密，在底部饅頭榫相對普拍枋發生滑移前，主要依靠斗拱的搖擺回轉變形耗散能量[10]。新型木制隔震裝置具有多級耗能特征：上部輕木結構的地梁板置于散斗頂部U形槽，在側向力作用下發生滑動；同時，在散斗底部的卯口為條形槽，泥道拱及華拱的榫頭在克服摩擦力后可以沿條形槽左右滑動，主要通過摩擦滑移耗散地震能量，當滑移至條形槽端部后，還可以利用木材的非線性特性進一步耗散地震能量。

為了研究該裝置的承載能力和耗能性能，對木制隔震裝置進行了水平及豎向靜載和低周反復荷載試驗。結果表明：該隔震裝置在豎向靜荷載作用下最終櫨斗劈裂破壞，承載力可達到80 kN。水平靜力加載力-位移曲線如圖3(a)所示，隔震裝置在水平向克服靜摩擦力后，具有較好的滑移及變形能力，最大水平側移可達116 mm，由于材料的非線性變形耗能，承載力大于滑動摩擦力。當側向位移幅值達36 mm時，在華拱和泥道拱2個側移方向的滯回曲線如圖3(b)，(c)所示。當華拱側向位移幅值達60 mm時，滯回曲線如圖3(d)所示。由圖3(d)可知，2個方向的滯回曲線都比較飽滿，具有良好的耗能能力。木制隔震裝置從開始受力就具有耗能能力，滯回環為梭形；當達到最大靜摩擦力后，榫頭開始在散斗的凹槽內滑動，水平力為滑動摩擦力；當達到滑移限值后，隔震裝置利用材料的非線性變形仍然可以產生更大側移，側向力有所增大。

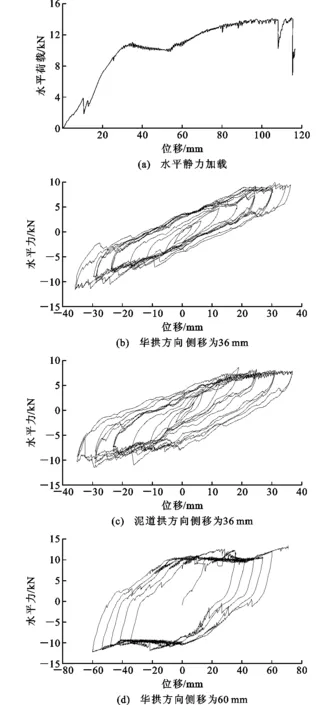
圖3 荷載-變形曲線Fig.3 Load-deformation Curves

2 多質點模型地震響應分析

以5層輕木-混凝土結構為工程背景，在2種結構的連接層設置木制隔震裝置，并利用Bouc-Wen恢復力模型[11-12]來模擬木制隔震裝置，建立該層間隔震結構的多質點模型，并進行地震響應分析。

2.1 輕木-混凝土結構方案

以某小學3層輕木結構校舍[13]為原型在底部添加2層混凝土結構形成5層木-混凝土混合結構，每層層高為3.6 m，長為26.4 m，寬為15.8 m，上部木結構平面布置如圖4(a)所示，下部混凝土采用C30，結構布置如圖4(b)所示，框架柱尺寸為400 mm×400 mm。設防烈度為8度，Ⅱ類場地，地面加速度為0.2g(g為重力加速度)，特征周期為0.45 s。

圖4 輕木-混凝土混合結構平面圖(單位：mm)Fig.4 Plan of Light Wood-concrete Hybrid Structure (Unit:mm)

2.2 隔震層的布置

在上下部結構連接處布置隔震層，由于隔震層承受上部木結構質量，根據試驗測得的木制隔震裝置豎向承載力及水平剛度進行了隔震層初步設計，共設置104個木制隔震裝置，華拱與橫軸一致，如圖5所示。

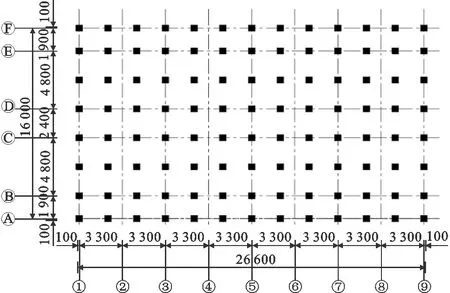
圖5 隔震裝置布置平面圖(單位：mm)Fig.5 Layout Plan of Isolation Dampers (Unit:mm)

2.3 層間隔振結構的多質點模型

由于結構具有對稱性，不考慮結構扭轉效應，根據木-混凝土層間隔震結構的振型及靜力作用下的變形特點，將隔震結構簡化為多質點剪切模型，如圖6所示，其中各層質量mi按各樓層的重力荷載代表值方法計算,kb為隔震層的剛度，隔震層質量mb為隔震層樓板質量與相鄰樓層半高度質量的和。

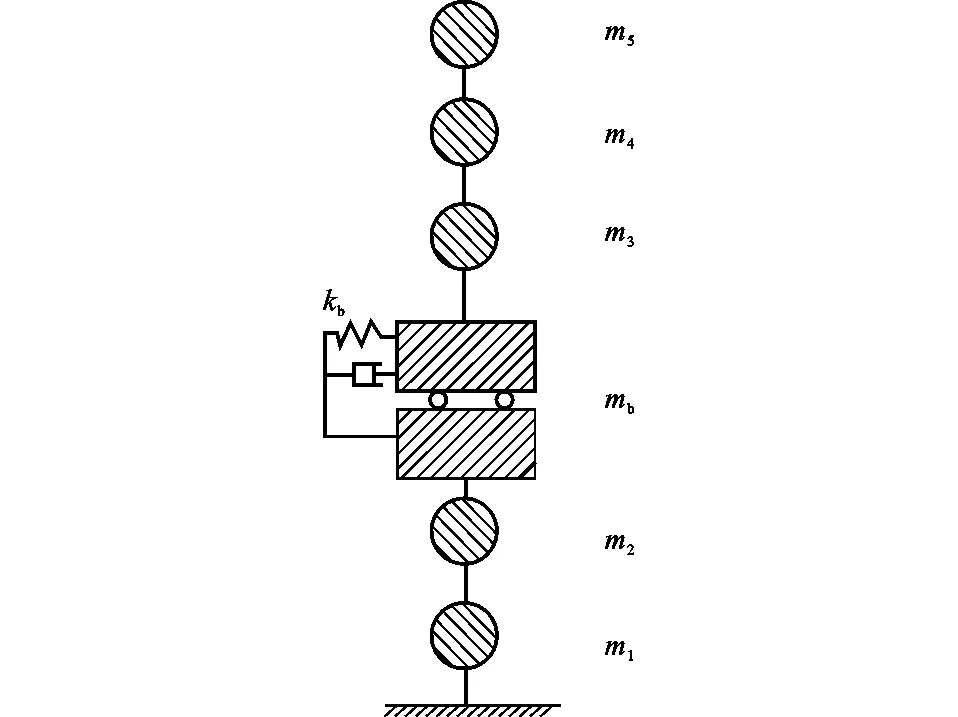
圖6 層間隔震結構的多質點動力模型Fig.6 Multi-lumped Mass Dynamic Model of Inter-story Isolation Structure

多質點模型混凝土結構的剛度根據D值法計算，輕木結構的各層剛度為各木剪力墻的剛度之和。各質點等效質量與側向剛度如表1所示，動力平衡方程為

(1)

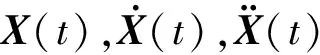
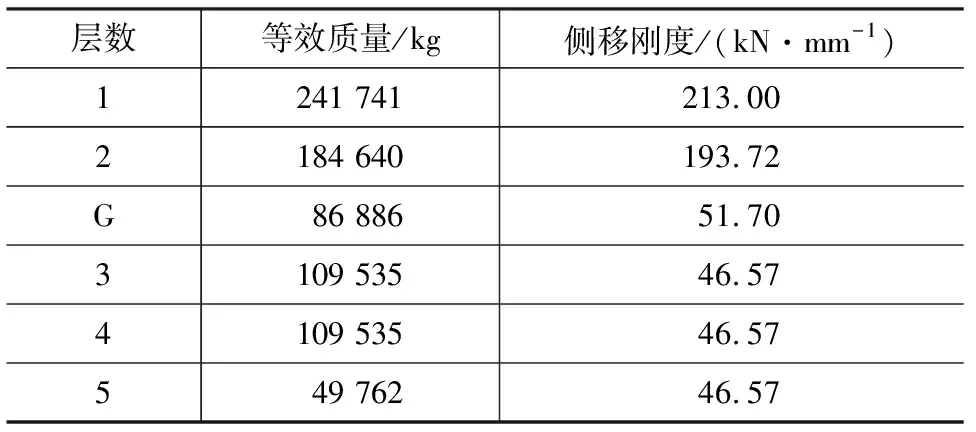
表1 結構的等效質量與華拱向側移剛度Tab.1 Equivalent Mass of Structure and Lateral Stiffness in Huagong Direction

注：G表示隔震層。

由于隔震層的阻尼與原結構相差很大，層間隔震結構為典型的非經典阻尼結構，故采用上下子結構法確定整體結構的阻尼系數矩陣，即將原結構在隔震層分為上下2個子結構，分別對子結構進行模態分析，計算各自的瑞雷阻尼矩陣Ct與Cb，而隔震層的耗能特性采用隔震支座的試驗結果，即擬合Bouc-Wen恢復力模型模擬，從而確定層間隔震結構的多質點動力模型。

2.4 地震波的選取

參照《建筑抗震設計規范》(GB 50011—2010)[14]，根據此建筑的II類場地條件選取El Centro波與唐山波2條強震觀測波作為地震輸入。分別將其加速度幅值調整至多遇、罕遇地震下對應的幅值，即0.7，4 m·s-2，地震波雙向輸入；2條地震波幅值為0.7 m·s-2時的加速度時程曲線如圖7所示。

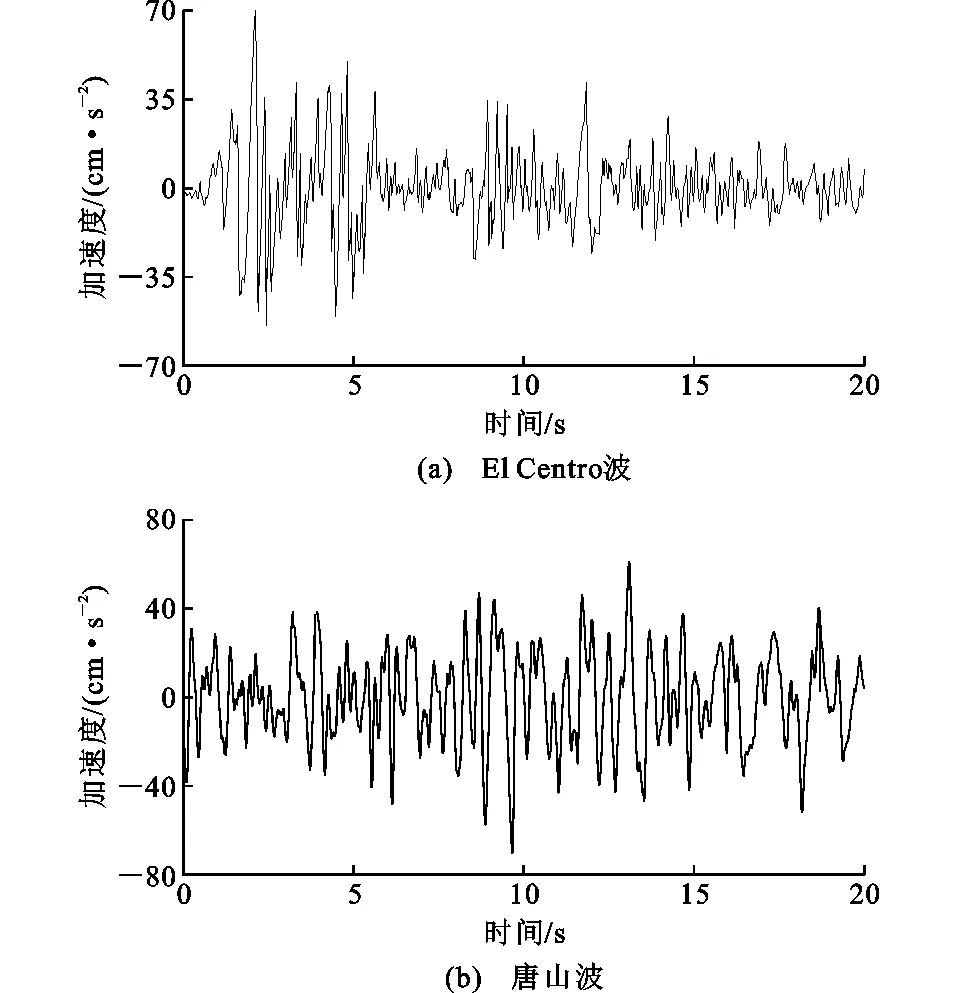
圖7 地震波加速度時程曲線Fig.7 Acceleration Time-history Curves of Seismic Wave

2.5 多遇及罕遇地震作用下多質點模型地震響應

采用自適應步長的4階龍格庫塔法[15]求解多質點模型的運動方程，并編制MATLAB程序計算在多遇與罕遇地震作用下的結構反應。

多遇地震作用下，El Centro波、唐山波作用下隔震層的滯回曲線分別如圖8(a),(b)所示。在多遇地震作用下，此隔震裝置能起到一定的減震效果，但由于地震力過小，無法使隔震支座產生充分的滑移，故減震效果并不理想。罕遇地震作用下，El Centro波、唐山波作用下隔震層的滯回曲線分別如圖9(a),(b)所示。

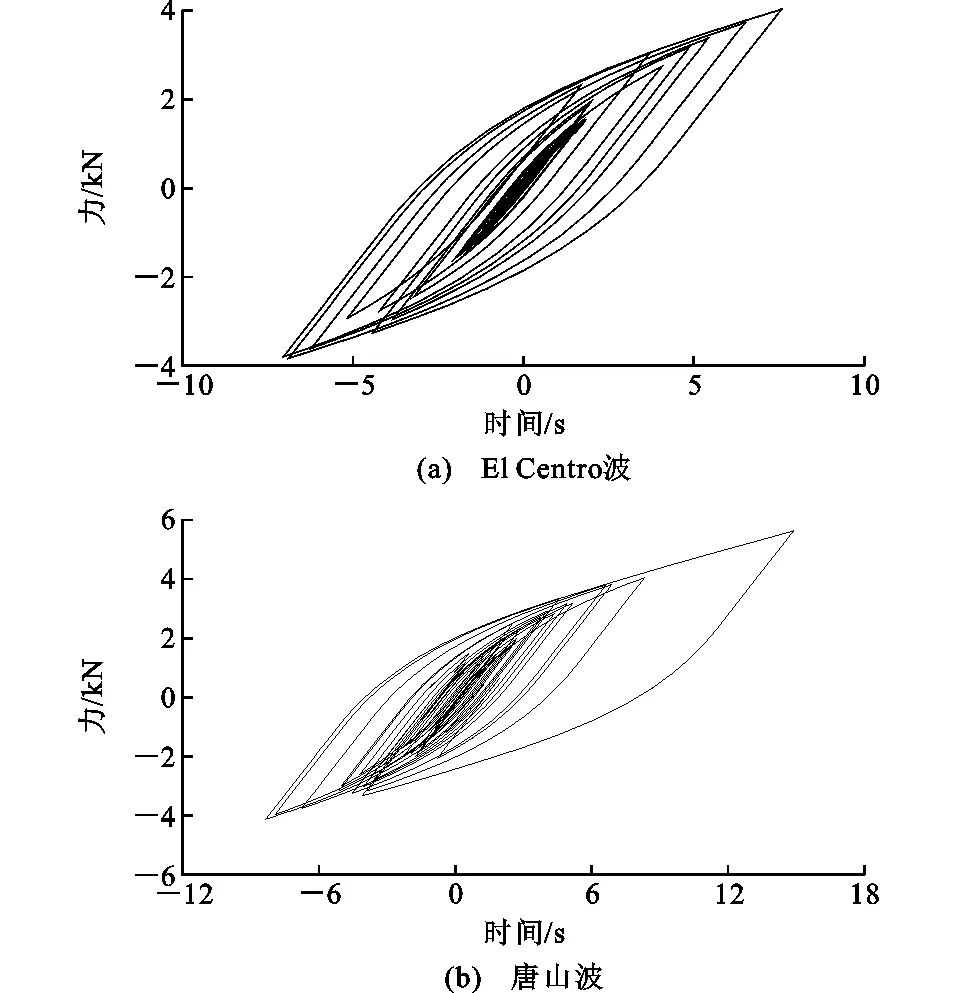
圖8 多遇地震下隔震裝置的滯回曲線Fig.8 Hysteretic Curves of Isolation Device Under Frequent Earthquakes

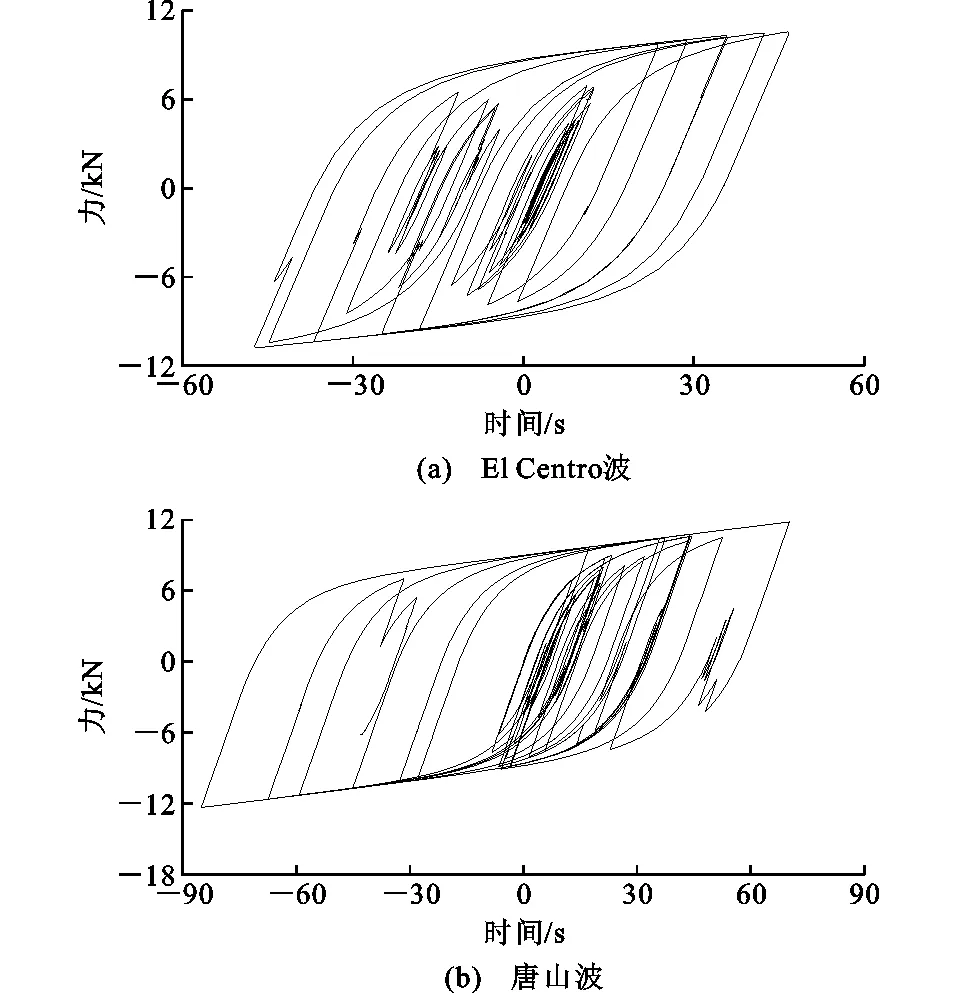
圖9 罕遇地震下隔震裝置的滯回曲線Fig.9 Hysteretic Curves of Isolation Device Under Rare Earthquake

由圖9可知，在罕遇地震作用下，隔震層的滯回曲線非常飽滿，表明隔震裝置已經進入塑性變形的強化階段，充分發揮了滑動與塑性二次變形的耗能能力，對上部木結構產生明顯的隔震作用。在El Centro波作用下，層間隔震結構與非隔震結構的頂點位移時程曲線比較如圖10所示。各層最大層間側移及最大加速度如表2，3所示。

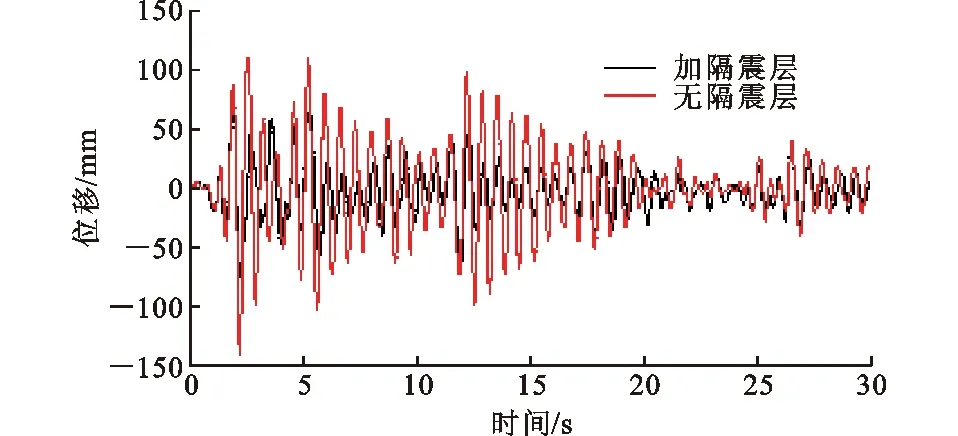
圖10 結構頂點處位移時程曲線Fig.10 Time-history Curves of Top Displacement

由圖10可知：原結構在地震作用下產生了劇烈的“鞭梢效應”，相比于低層混凝土結構，輕木結構的層間側移及加速度都被明顯放大；設置此隔震裝置后，減震效果明顯。隔震結構的頂點位移比原結構減小了47.2%，除隔震層外，其他各層的層間側移都有明顯減小，尤其是首層輕木結構的層間側移僅為原結構的44.35%；上部木結構的加速度也明顯減小，首層木結構加速度值不及原結構的50%，但混凝土結構的加速度減小非常有限，甚至在唐山波作用下略有放大。

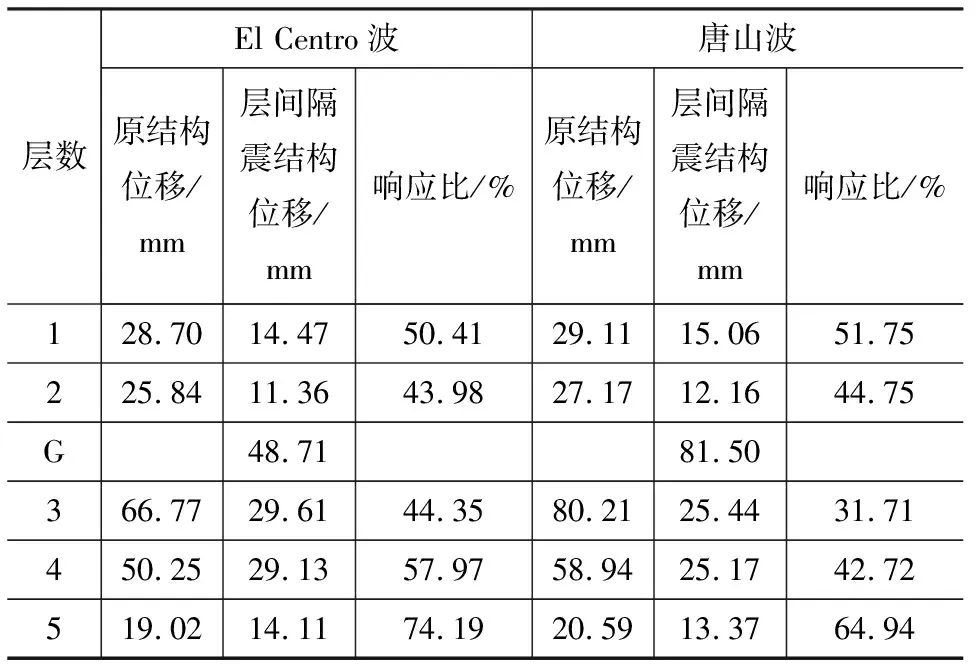
表2 華拱向最大層間位移Tab.2 Maximum Inter-story Drift in Huagong Direction

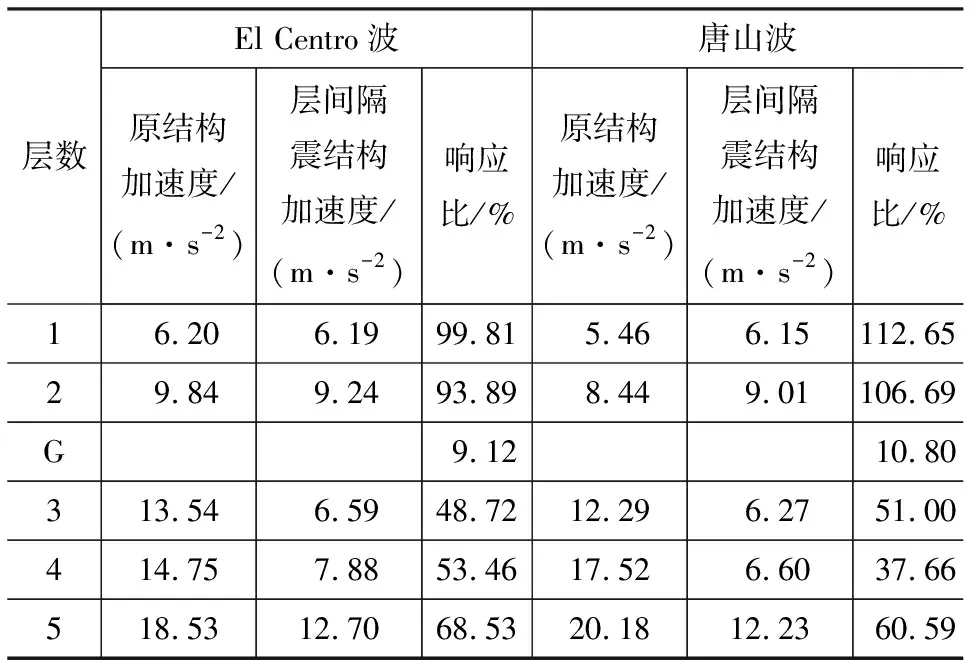
表3 華拱向最大絕對加速度Tab.3 Maximum Absolute Acceleration in Huagong Direction

3 基于三質點模型的參數優化分析

雖然設置木制隔震裝置的輕木-混凝土混合結構已經具有明顯的減震效果，但是上部輕木結構較柔，明顯存在一定的振動響應，而且下部混凝土結構有加速度放大的現象，因此有必要進行參數優化，選取合適的隔震層剛度與阻尼以提高隔震效果。層間隔震結構的參數優化常采用兩質點[16]或多質點等效模型，由于上部結構較柔，不能將其視為剛體移動，故采用三質點模型以考慮上部結構的振動響應。

3.1 層間隔震結構的等效三質點模型

將上部結構、隔震層及下部結構分別等效為1個質點，形成三質點動力模型，如圖11所示。隔震層與隔震層以上結構質點的相對位移便可反映上部木結構的地震響應。

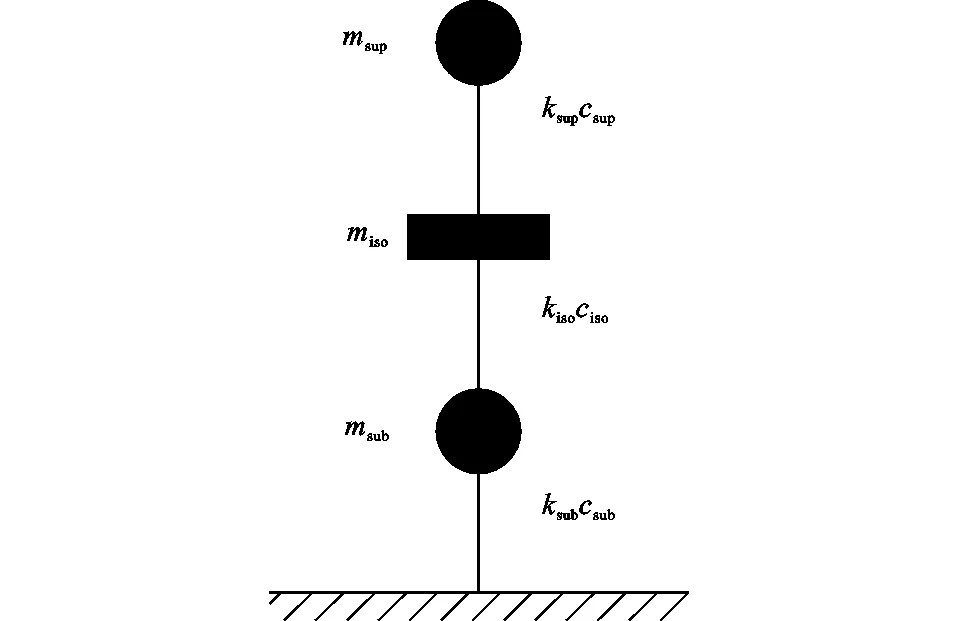
圖11 三質點模型Fig.11 Three-lumped Mass Model

上下部子結構的等效質量msup，msub及等效剛度ksup，ksub的等效簡化采用以下方法[17]：首先求解上下部子結構的各階頻率ωi(i=1,2,…,n)與對應的各階振型φi(i=1,2,…,n)，計算等效質量meq與等效剛度keq為

(2)

(3)

式中：r為將地面位移與模型自由度耦合的影響向量；φ1為第1階振型。

由此分別得到上、下部子結構的等效質量msup，msub與等效剛度ksup，ksub。

上、下部子結構的阻尼系數c為

c=2meqω1ξ

(4)

式中：ξ為子結構的阻尼比，文中均取0.05。

隔震層的質量miso與等效剛度kiso通過試驗確定。隔震層阻尼系數ciso為

ciso=2(miso+msup)ωisoξiso

(5)

(6)

式中：ξiso為隔震層等效黏滯阻尼比，通過試驗確定。

模型等效后，三質點模型與多質點模型周期對比如表4所示。

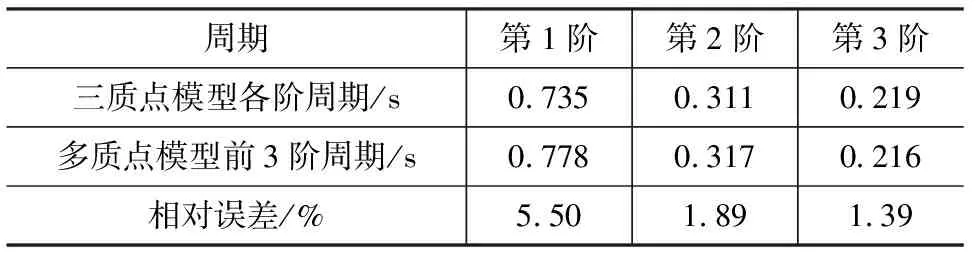
表4 三質點模型與多質點模型周期對比Tab.4 Comparison of Periods Between Three-lumped Mass Model and Multi-lumped Mass Model

由表4可知，三質點模型與多質點模型的前3階周期十分接近，相對誤差皆在6%以內，表明此簡化模型可以準確反映結構的前3階模態。

3.2 層間隔震的參數優化分析

隔震層的參數優化設計采用頻域分析法[18-20]。對于層間隔震結構通常選取基底剪力為最優控制目標[21]。假設輸入的地震波是均值為0的平穩隨機過程，則系統的響應也是均值為0的平穩隨機過程。分別以基底剪力F、上部結構層間側移及下部結構加速度為最優控制目標，經過傅里葉變換，并取隔震層質量為單位1，計算可得剪重比的均方差為

μsubRe(Ha1(iω)Ha2(iω))+

2μsupRe(Ha2(iω)Ha3(iω))+

μsupμsubRe(Ha2(iω)Ha3(iω))]dω}/g

(7)

下部結構絕對加速度均方差為

(8)

上部結構層間側移的均方差為

|H3(iω)|2+2Re(H2(iω)H3(iω))]dω}

(9)

式中：比例參數μsup，μsub分別為上、下部結構與隔震層質量比；Ha1，Ha2，Ha3分別為質點msub，miso，msup的絕對加速度傳遞函數；H2，H3分別為miso，msup的位移傳遞函數；ω為頻率；σ(·)為均方差。

對于既定結構，μsub，μsup，ωsub，fsup4個參數為恒定值，隔震層參數ξiso，fiso為待定控制參數。

對于本文的木混結構，根據上下部的結構質量及剛度，可計算既定參數(表5)。

表5 三質點簡化模型參數Tab.5 Parameters of Three-lumped Mass Simplified Model

注：ωsub為下部結構頻率；fsup為上部結構與下部結構的頻率比。

在給定結構參數的情況下，可以繪制剪重比、下部結構絕對加速度(上部結構層間位移)與隔震層阻尼比ξiso及頻率比fiso關系的三維圖像，見圖12。

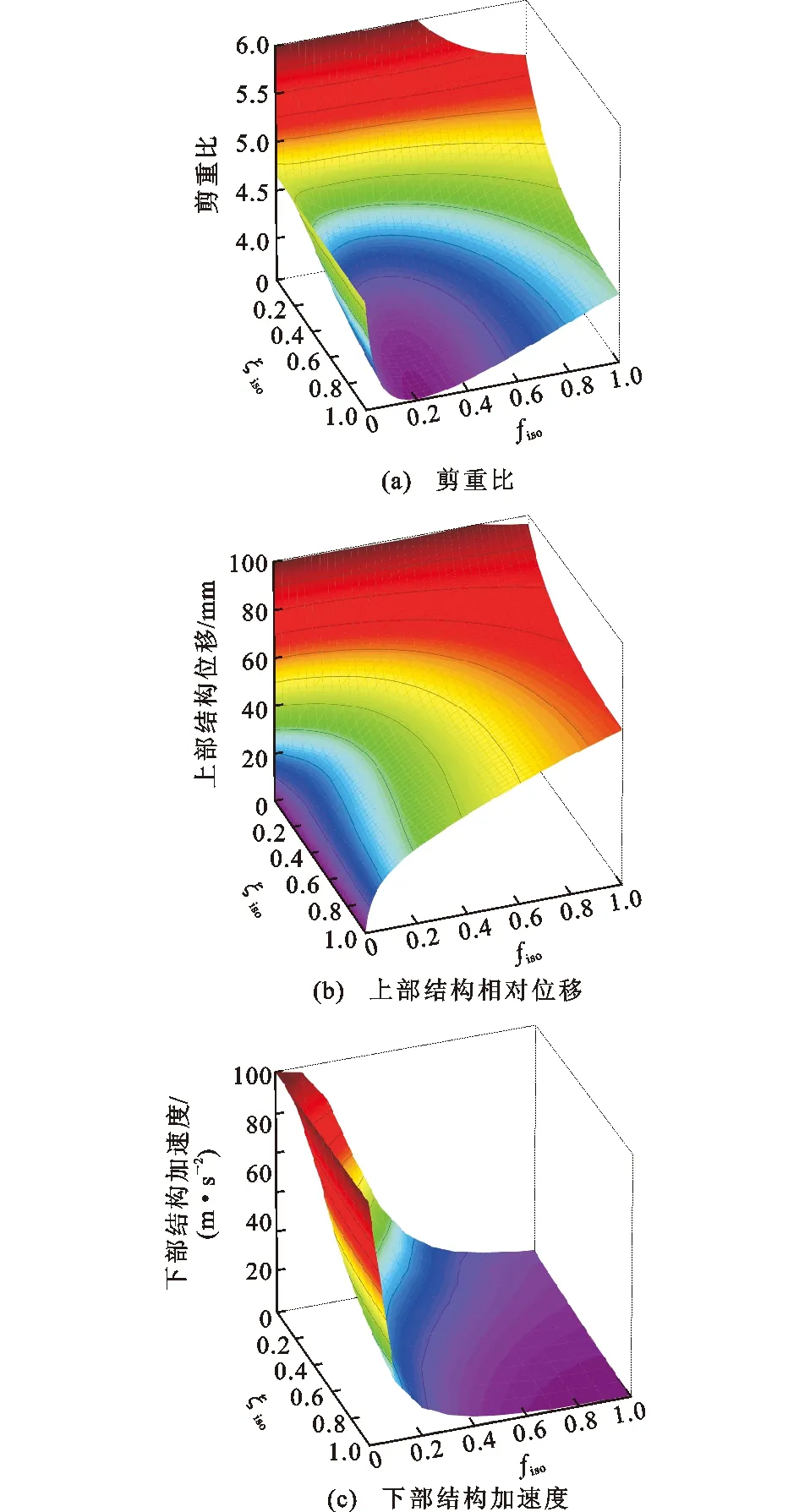
圖12 三性能指標-頻率比-阻尼比關系Fig.12 Relationship of Three Performance Indicators, Frequency Ratio and Damping Ratio

由圖12(a)可知:當隔震層阻尼比為0時，基底剪力隨著頻率比的增大呈下降的趨勢；在非0情況下，隨著阻尼比的增大，基底剪力不斷減小，但減小速度不斷放緩；當阻尼比大于0.2后，增大阻尼比對基底剪力的影響有限。當頻率比為0時，基底剪力為固定值，改變阻尼比對基底剪力沒有影響；隨著頻率比的增大，基底剪力迅速減小；當隔震層頻率比位于0.2附近時，基底剪力達到最小，當頻率比大于0.2后，又開始逐漸增大，頻率比處于0.2～0.4區間；阻尼比大于0.1時，基底剪重比均控制在4.0以下。由圖12(b)可知，當頻率比與阻尼比均為非0時，上部結構的層間位移隨著頻率比的增大而增大，隔震層剛度越小，上部結構的位移越能得到有效抑制。當頻率比小于0.7時，相對位移首先隨著阻尼比的增大而減小至最小值，然后隨著阻尼比的增大而有輕微增大。因此對于不同的頻率比存在不同的最優阻尼比，如隔震頻率比為0.3時，隔震層最優阻尼比約為0.42；頻率比為0.2時，最優阻尼比為0.31，最優阻尼比在一定范圍內時，相對位移都可得到有效控制。更為關鍵的是頻率比的控制，當頻率比小于0.4、阻尼比大于0.15時，結構的相對位移均可控制在原結構的50%以下；當頻率比小于0.3、阻尼比大于0.2時，僅為原結構的1/3。

由圖12(c)可知，下部結構的加速度響應隨著隔震層阻尼比、頻率比的增大而減小。當隔震頻率越小、隔震層越柔，下部結構的加速度越可能出現增大。在進行隔震設計時，應控制隔震層的剛度不宜過柔，適當增大阻尼比以減小下部結構的加速度。數據分析表明：當頻率比大于0.2、阻尼比大于0.1時，下部結構的加速度均小于原結構。

綜上所述，依據剪重比、上部結構相對側移及下部結構加速度，可以取隔震層最優頻率比在0.2～0.4區間，最優阻尼比根據頻率比的不同在0.15～0.4區間確定。

4 結語

(1)新型木制隔震裝置既傳承古建筑斗拱的構造特點，又適用于現代木結構，具有潛在的工程應用價值。試驗結果表明：木制隔震裝置具有足夠的水平豎向承載力及良好的耗能能力。

(2)采用木制隔震裝置對上木下混混合結構進行層間隔震，并采用多質點動力模型進行地震響應分析，結果表明：在多遇地震作用下，結構幾乎處于彈性階段，隔震裝置未發生滑移，減震效果不明顯；在罕遇地震作用下，隔震支座產生了充分的滑移，并進入二次變形階段，滯回曲線飽滿，耗能充分，但下部結構存在加速度放大現象。

(3)分析隔震層參數對上木下混隔震體系隔震效果的影響，以上層結構層間位移、下部結構加速度及底部剪力為最優控制目標，進行參數優化分析，結果表明：隔震層最優頻率比在0.2～0.4區間，最優阻尼比根據頻率比的不同在0.15～0.4之間確定，結構的減震效果可以達到最優。