非線性光學中的暗孤子分子*

徐丹紅 樓森岳

(寧波大學物理科學與技術學院, 寧波 315211)

孤子分子是當前非線性光學中的重要課題.本文首先研究具有高階色散和高階非線性效應非線性光學模型中各種周期波(孤子晶格)的嚴格解, 及各種可能的單孤子解.然后在一個可積的情況下, 利用推廣的雙線性形式, 給出多孤子解, 并從多孤子解的速度共振條件給出暗孤子分子的嚴格解析表達式.對于本文給出模型的多暗孤子分子之間, 以及孤子分子和通常孤子之間的相互作用都是彈性的.值得指出的是, 在不可積的情況下孤子分子也是可以存在的.

專題：非線性物理

1 引 言

孤立波、孤立子、呼吸子、怪波等非線性局域激發模式在物理學的各個分支如流體物理[1]、等離子體物理[2]、復雜系統和復雜網絡[3]、量子場論和粒子物理[4]、引力理論[5]、玻色愛恩斯坦凝聚[6]、大氣和海洋物理[7]、特別是光物理[8?10]中起著非常重要的作用.最近, 孤子分子在非線性光學實驗上的成功發現[11?13]成為非線性物理的一個新的熱門課題.在理論上, 非線性耦合系統的孤子分子已經被一些非線性物理工作者所研究[14,15].除了在光學中的孤子分子外, 在其他領域也應該能找到孤子分子.在文獻[16]中, 本文作者之一(樓)在單分量的流體模型中給出了多種類型的孤子分子解.

非線性系統孤子解的求解有很多行之有效的方法, 如廣田(Hirota)直接法[17]、達布 (Darboux)變換方法[18]、反散射變換方法[19]、對稱性方法[20]等等.通常使用不同的方法得到的多孤子解表面上看可以是很不一樣的, 但本質上都是等價的.不同的表達式在應用中各有優點.絕大多數文獻中, 各種非線性模型的單孤子解都采用緊致簡潔方便的雙曲函數形式, 因此很多著名專家如Hirota 和Toda 及我國的陳登遠[21]等都期望能用雙曲函數來簡潔地表達多孤子解, 最近, 我們成功實現這一愿望[7,22].這些新的簡潔表達式不僅研究非局域非線性系統的孤子解非常方便, 而且本文將進一步用這種表達式來尋求各種類型的共振孤子, 包括孤子分子.

本文第二節首先給出具有高階色散和高階非線性修正的非線性光學系統.然后研究該系統可能具有的周期波解和孤立波解.本文第三節中研究一個可積的情況— 散焦型 Hirota 模型, 將Hirota模型變換成一個新的Hirota 雙線性方程后, 成功給出用雙曲余弦描述的多暗孤子表達式.然后從多孤子解出發研究一種新的共振孤子激發模式—速度共振.從而導致孤子束縛態—暗孤子分子的形成.暗孤子分子之間及暗孤子分子和通常暗孤子的相互作用性質也在第三節做了簡單的討論.最后一節是總結和討論.

2 高階非線性薛定諤方程及其周期波和孤立波

在眾多的實際非線性光學問題中高階的色散和各種非線性效應是不可忽略的.其中最常見的高階非線性薛定諤方程可具有下述形式

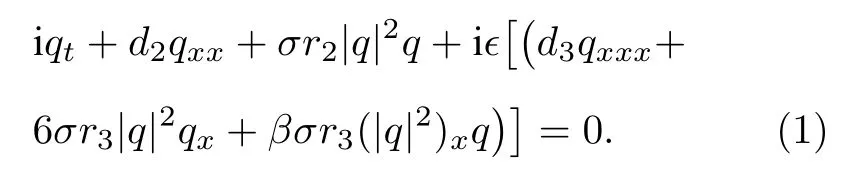
方程(1)包含了很多物理和數學領域中重要的特殊情況 (包括時空變量t和x的交換).?=0 對應的正是著名的聚焦(σ=1 ) 和散焦(σ=?1 )非線性薛定諤方程.當d2=r2=0,β=0,3 時, 方程(1) 是另一個非常重要的物理和數學中的重要模型: 復修正 Korteweg de-Vrise (KdV) 方程[23].當β=0時, 方程 (1)是可積的 Hirota 方程[24].當β=3時, 方程 (1)也是可積系統: Sasa-Satsuma 方程[23].當r2=d3=0 時, 方程 (1)也包含了三種可積的導數非線性薛定諤方程[25].

在研究高階非線性薛定諤方程的多孤子解和孤子分子解之前, 我們先研究一般高階非線性薛定諤系統(1)式 下述形式的一般行波解

其中k0,ω0,?0,k,ω及ξ0為待定實常數.

將(2) 式代入(1)式可得關于Q(ξ) 應滿足的兩個常微分方程,

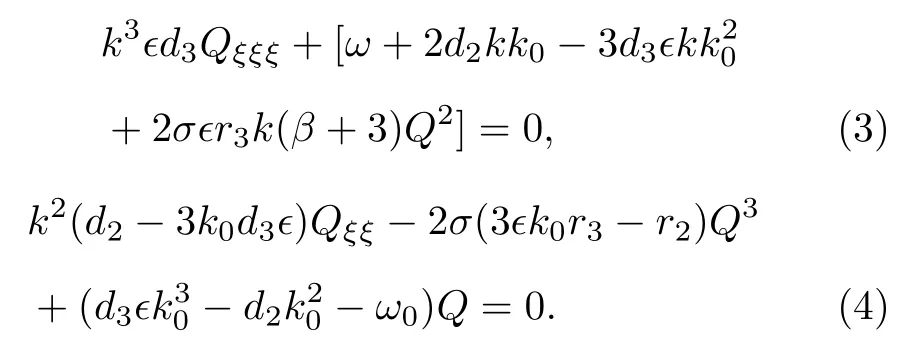
為了給出(3)式和(4)式的相容顯式解我們分兩種情況:

情況1一般情況.在對模型參數無任何限制的情況下, 可取載波參數k0和ω0由其他參數決定為

在參數條件(5)式和(6)式下, 方程(3)和(4)退化成單個標準的Jacobi橢圓函數滿足的方程

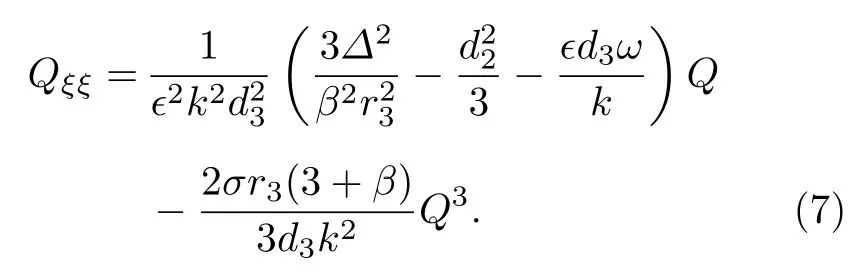
方程(7)有三種標準的周期波解:

周期波解1

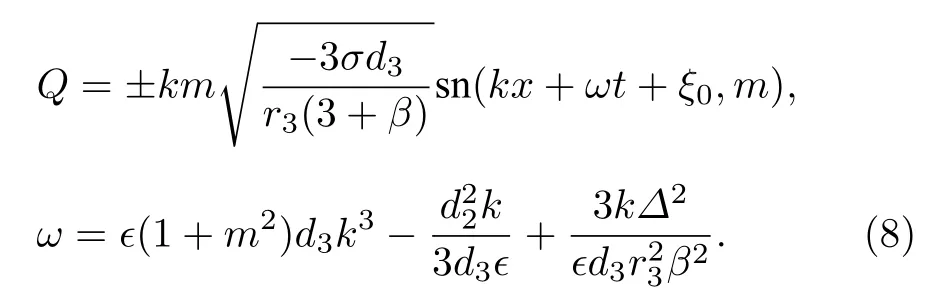
周期波解2

周期波解3

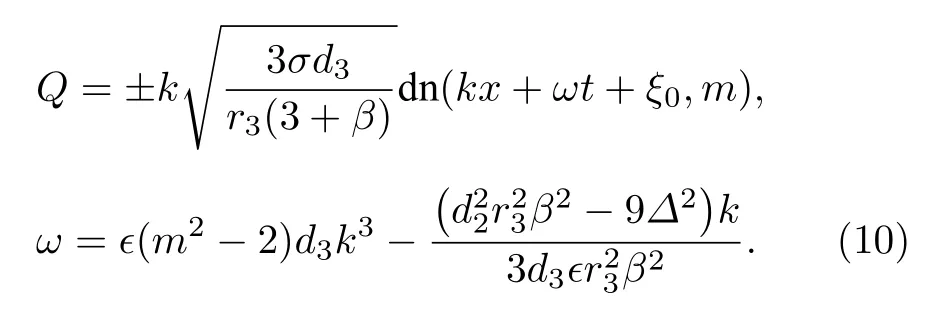
當Jacobi橢圓函數的模趨向于1時, 上述三類周期波解退化成兩種類型的孤立子解.

孤子解1, 暗孤子解

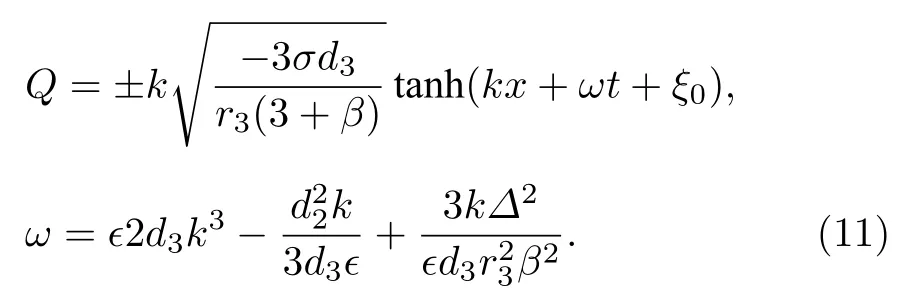
孤子解2, 亮孤子解

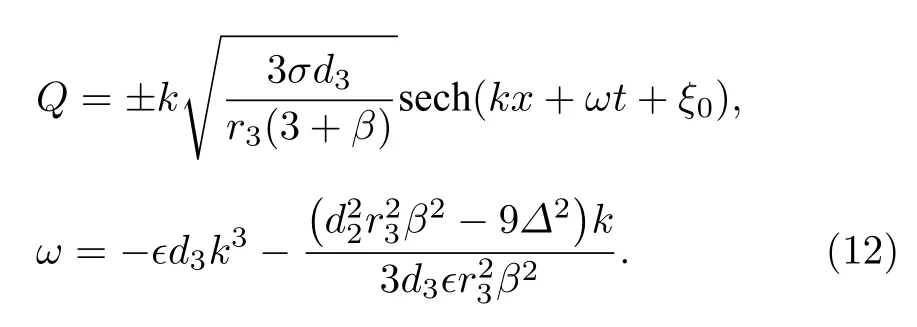
從解的表達式很容易看出, 暗孤子晶格解(8)式和暗孤子解(11) 式的存在條件是亮孤子晶格(9)式, (10)式 和亮孤子(12)式存在條件是

情況2特殊情況?=0 .在這一特殊參數條件下光孤子系統(1)具有更一般的孤子晶格和孤子解.當?=0 時, 可簡單取

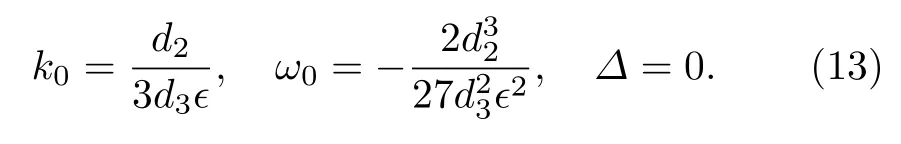
在參數條件(13)式下, 方程(3)和(4)退化成單個三階方程

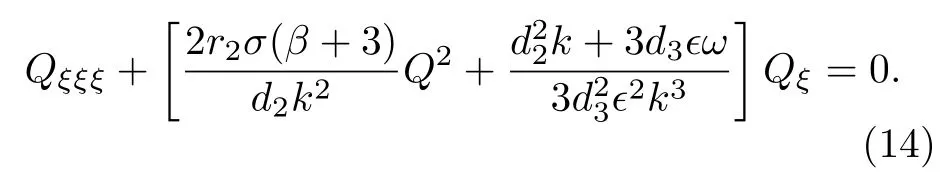
類似地, 方程(14)有三種標準的周期波(孤子晶格)解:

周期波解4

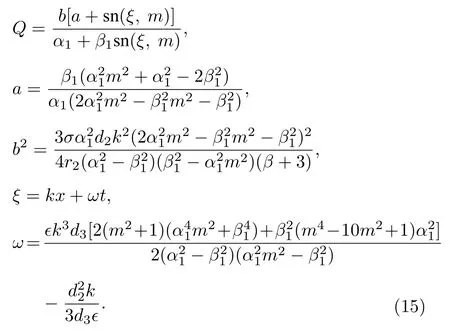
對于小的m, Jacobi橢圓函數sn接近于三角函數sin.而隨著模m越來越接近于1, sn越來越接近于雙曲tanh函數, 而相應的周期解就看起來像是孤立子的周期性排列.因此對于接近于m= 1的周期解, 也可以稱之為孤子晶格解.圖1 展示了用(15) 式描述的周期波解、亮孤子晶格解.其相應的參數為(本節所有的圖中的模型參數固定為β=d2=d3=r2=10?=1)

圖2展示了用同一表達式(15)式 描述的暗孤子晶格解.其相應的參數為

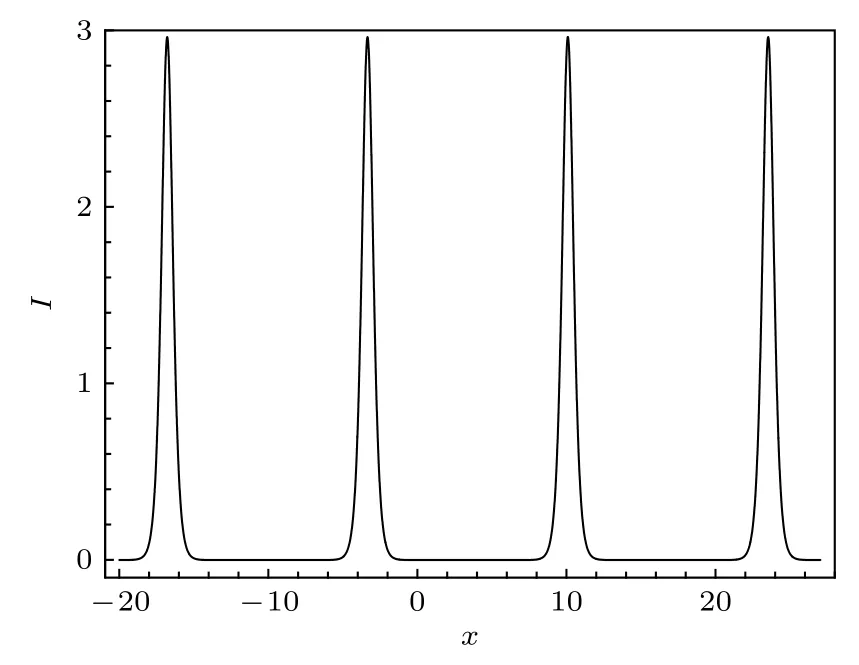
圖1 由 (15) 式描述的亮孤子晶格, 其中參數由 (16) 式給定Fig.1.Bright soliton lattice described by Eq.(15) with the parameter selected from Eq.(16).

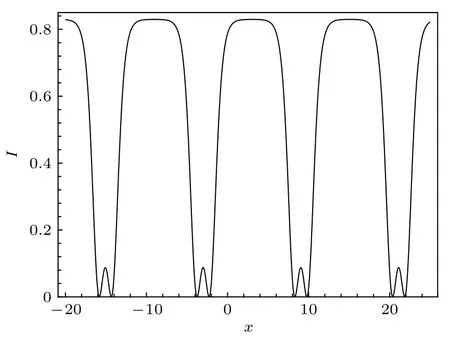
圖2 由 (15)式描述的暗孤子晶格, 其中參數由 (17) 式給定Fig.2.Dark soliton lattice described by Eq.(15) with the parameter selected from Eq.(17).

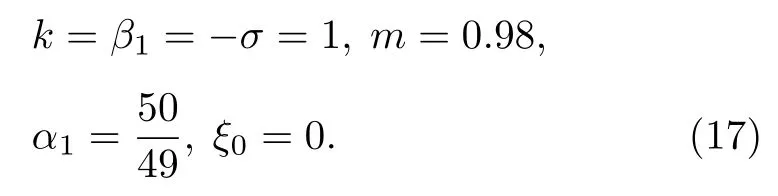
這類暗孤子晶格中的暗孤子中間有一非暗的灰色區.

周期波解5

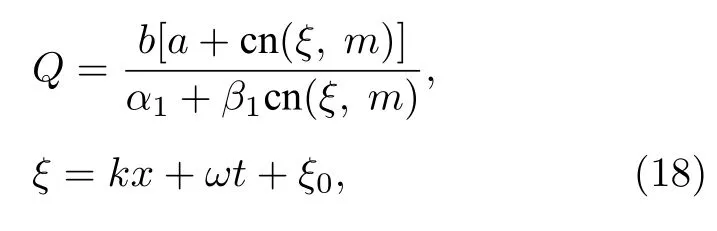
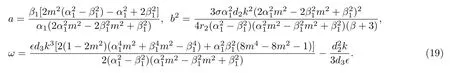
圖3 展示了第二種類型的亮孤子晶格結構.這類亮孤子晶格由表達式(18) 式描述.與圖3對應的參數為

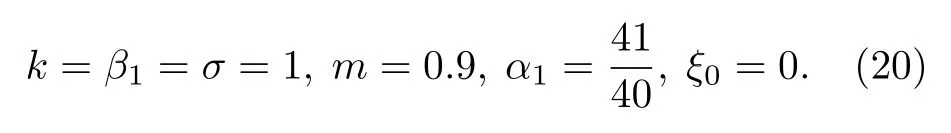
第一類的亮孤子晶格的背景是暗的, 第二類亮孤子晶格的背景是灰的, 而灰色背景和亮孤子間又有暗區相間.

周期波解6

由于Jacibi橢圓函數dn的恒正性, 這類函數描述的孤子晶格既可以是亮孤子晶格, 也可以是暗孤子晶格.

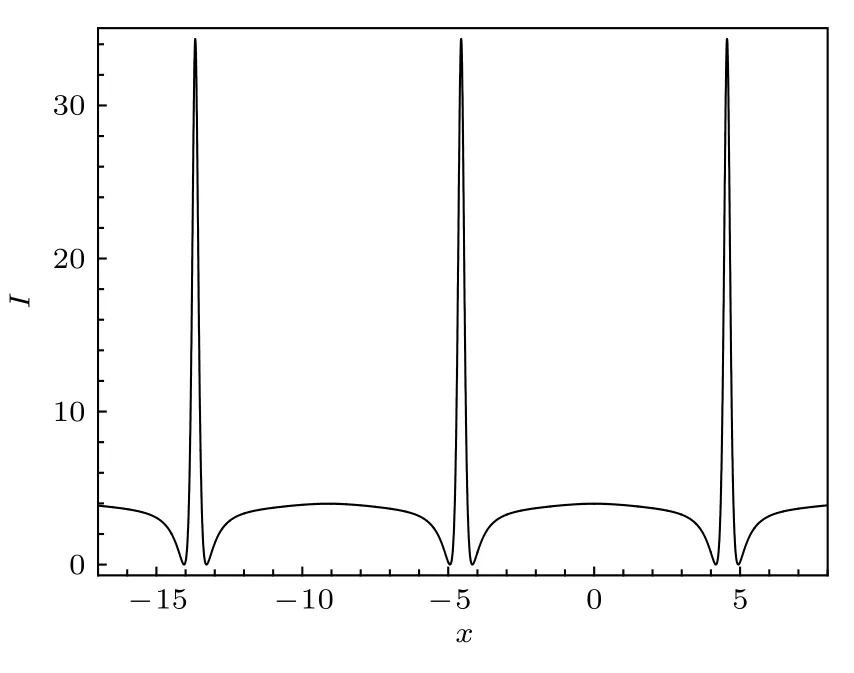
圖3 由 (18) 式描述第二類亮孤子晶格, 其中參數由(20)式給定Fig.3.Second type of bright soliton lattice described by Eq.(18) with the parameter selected from Eq.(20).

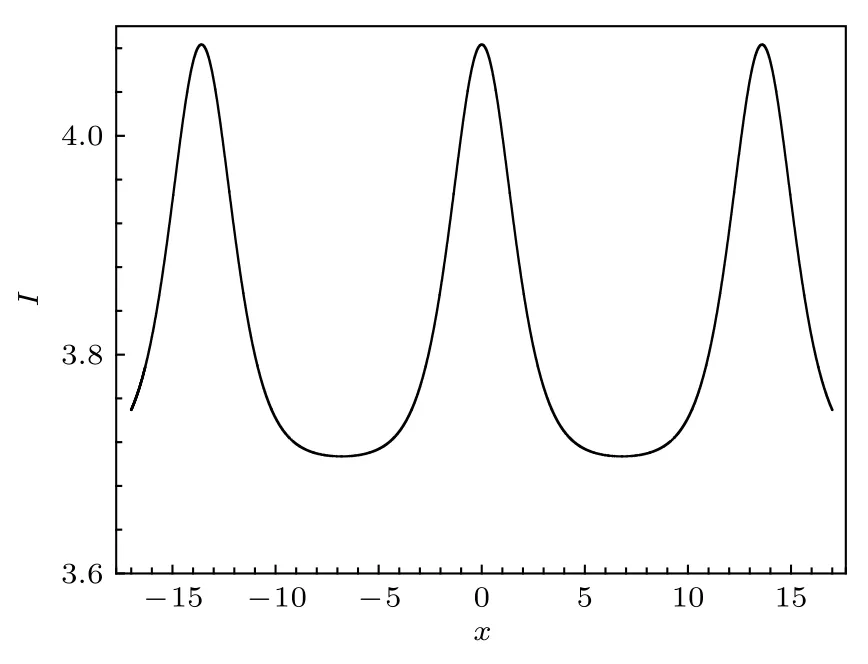
圖4 第三類亮孤子晶格.由 (21) 式描述, 其中參數由 (23) 式給定Fig.4.Third type of bright soliton lattice described by Eq.(21) with the parameter selected from Eq.(23).

圖4 展示了第三種類型的亮孤子晶格結構.這類亮孤子晶格由表達式(21)式 描述.與圖4對應的參數為

這一類亮孤子也具有灰色背景, 但不同于第二類亮孤子晶格, 灰背景和亮孤子之間沒有暗區隔離.

圖5展示了第二類暗孤子晶格結構.這類暗孤子晶格由表達式(21) 式描述.與圖5對應的參數為

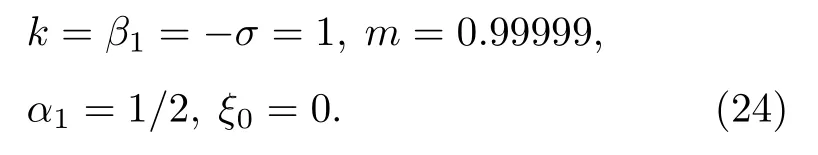
當 Jacobi橢圓函數的模m→1 時, 周期波解(15)退化為下述孤子解:

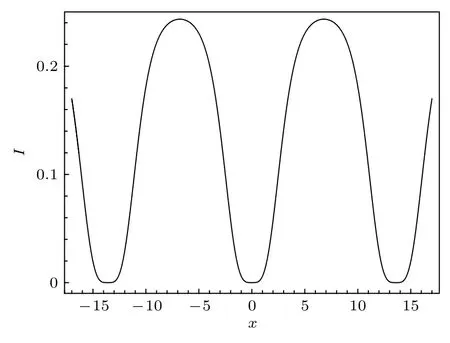
圖5 第二類暗孤子晶格由 (21)式描述, 其中參數由 (24)式給定Fig.5.Second type of dark soliton lattice described by Eq.(21) with the parameter selected from Eq.(24).

孤子解3

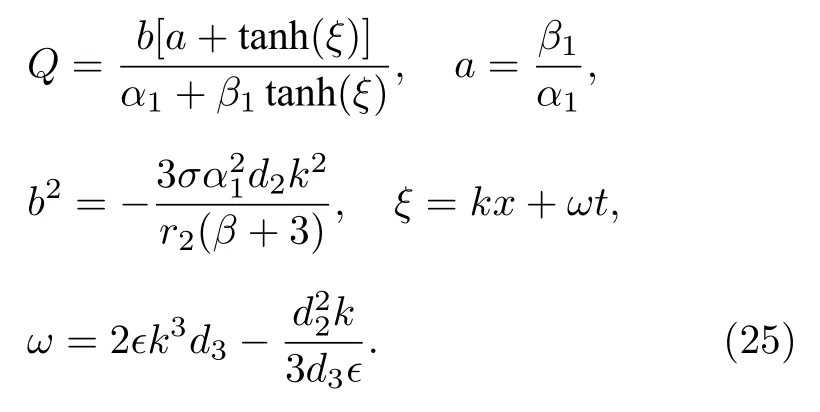
暗孤子解 (25) 式的實條件和非奇異條件為

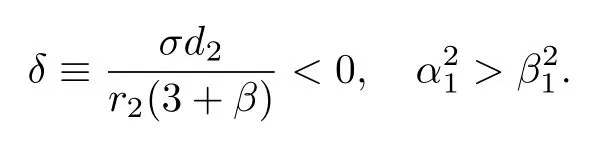
圖6正是與(25)式對應的暗孤子解, 相應的參數為

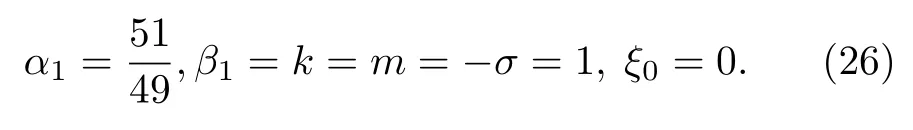
周期波解(18)式和(21)式退化成同一種孤子解:

孤子解4:

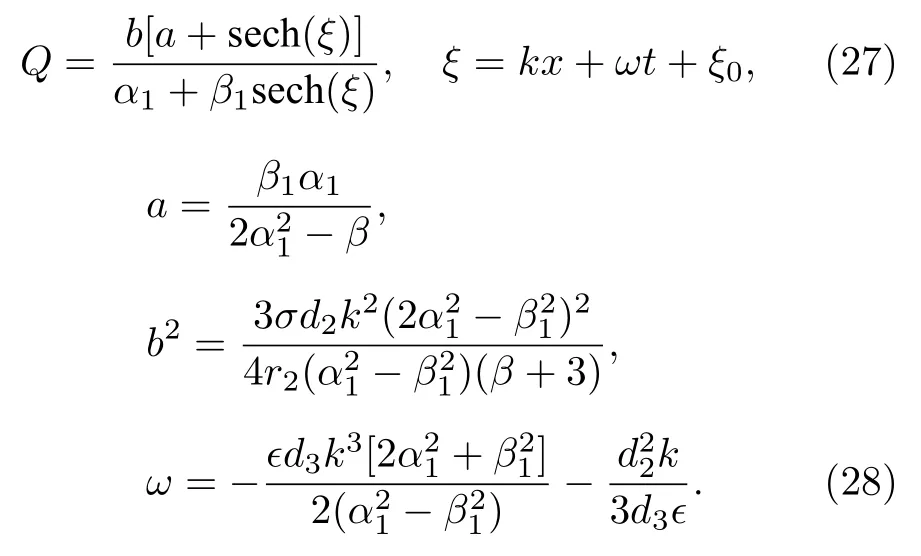
當參數滿足下述條件

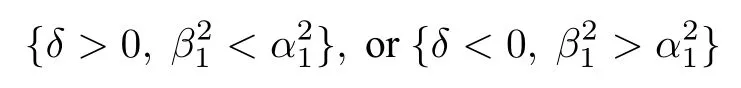
時, 孤子解 (27) 式是一個具有灰背景的亮孤子.

圖7展示的正是由(27)式表示的具有灰背景的亮孤子, 其中的參數為

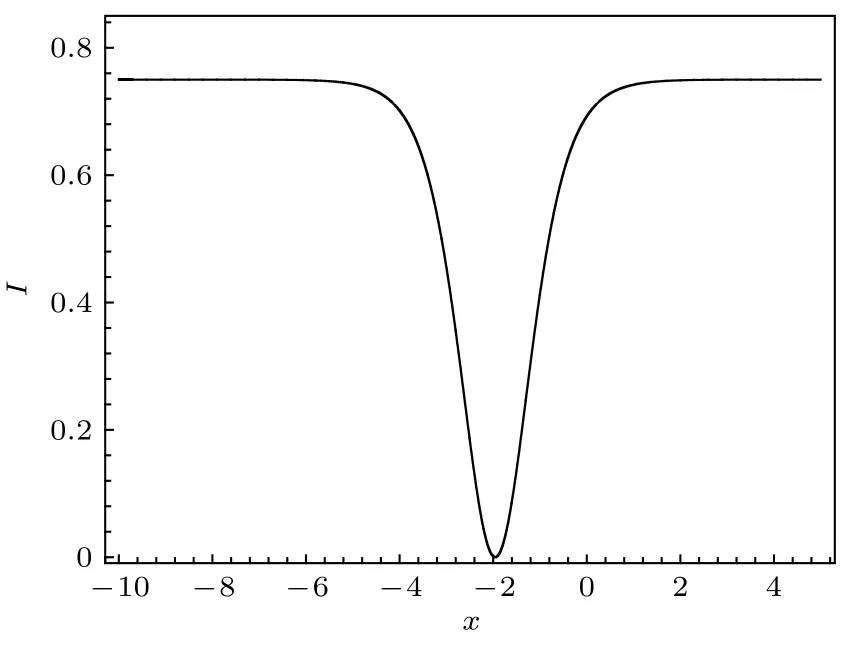
圖6 由 (25) 式描述的暗孤子, 其中參數由 (26) 式給定Fig.6.Dark soliton described by Eq.(25) with the parameter selected from Eq.(26).

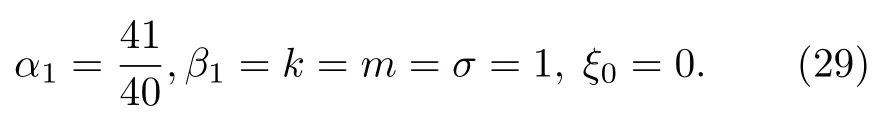
當下述條件

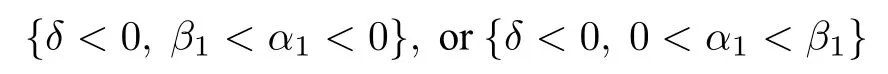
滿足時, 孤子解 (27) 式是一個灰孤子解.當β1=2α1時, 孤子解 (27) 式是一個暗孤子.

圖8展示了由(27)式表示的暗孤子, 其中的參數取為

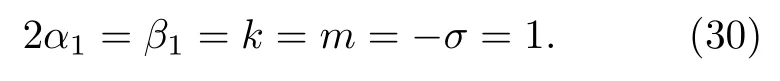
如圖8所示的暗孤子具有一特殊的性質, 即在暗孤子中心x=0 前三階變化率均為零:I(x=0)=Ix(x=0)=Ixx(x=0)=Ixxx(x=0)=0.

特別有意義的是表達式(27)式具有共振孤子相同的形式, 因此對于某些參數區間可知(27) 式也具有暗孤子分子的形式.圖9顯示了由(27)式描述的孤子分子的性質, 其中的參數選擇為

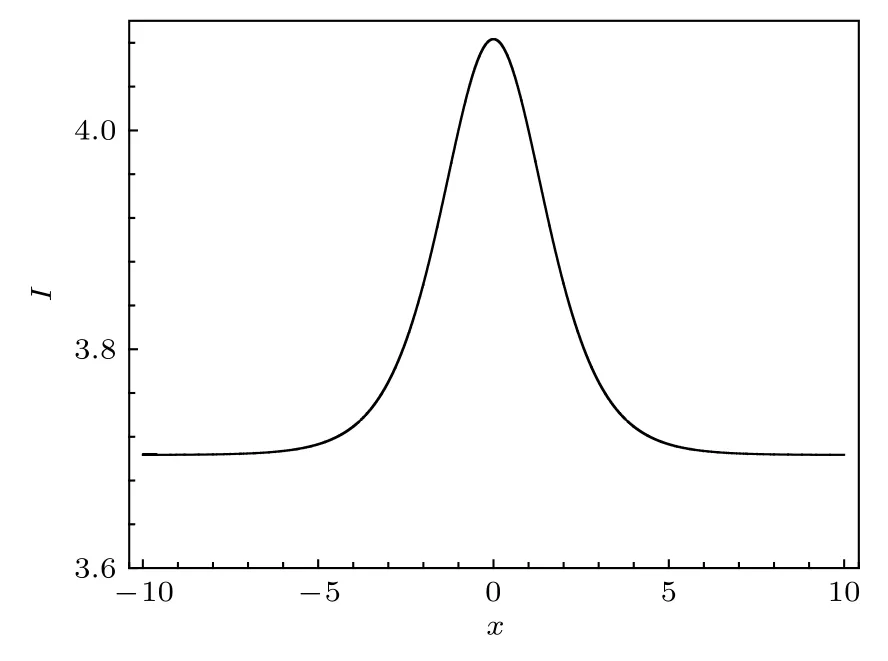
圖7 由 (27) 式描述的具有灰背景的亮孤子, 其中參數由(29)式給定Fig.7.Bright soliton (with gray background) described by Eq.(27) with the parameter selected from Eq.(29).

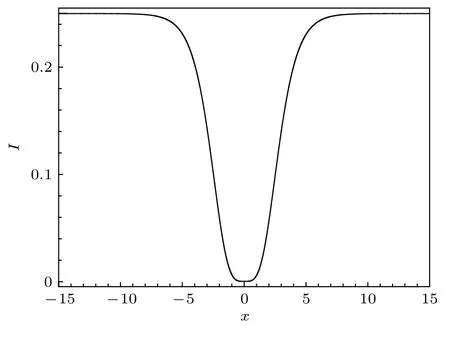
圖8 由 (27)式描述的暗孤子, 其中參數由 (30)式給定Fig.8.Dark soliton described by Eq.(27) with the parameter selected from Eq.(30).

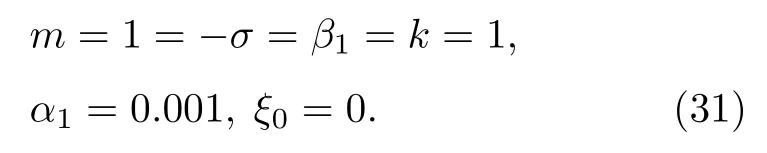
由于β0,3 時, (1) 式不是可積系統, 所以孤子分子可以在不可積系統中存在.

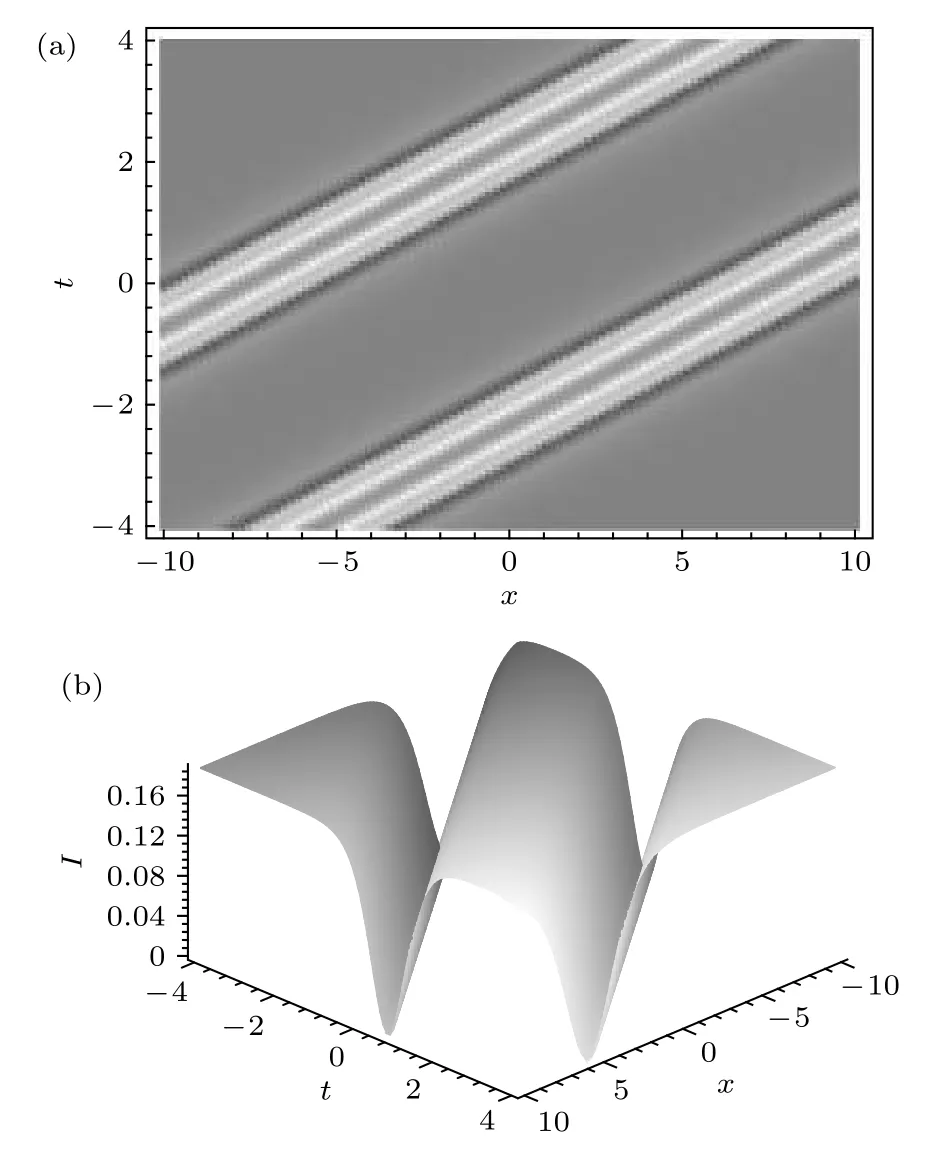
圖9 (a)由 (27) 式描述的暗孤子分子的密度圖; (b) 與(a)對應的立體圖, 圖中參數由 (31)式給定Fig.9.(a)Density plot of the dark soliton molecule described by Eq.(27) with the parameter selected from Eq.(31); (b) three dimensional plot related to Fig.(a).

3 散焦Hirota系統的多孤子解及其孤子分子解

為了研究孤子分子的性質, 本節只限定于一個特殊的可積系統, Hirota系統, 其對應的參數限制為

對于可積系統, 可以用很多方法得到其多孤子解,如Hirota 方法、反散射方法、黎曼-希爾伯特方法、達布變換方法等等.所有各種方法中, Hirota方法是最簡單明了的方法.

很容易驗證, Hirota系統在變換

下可以變為其雙線性形式

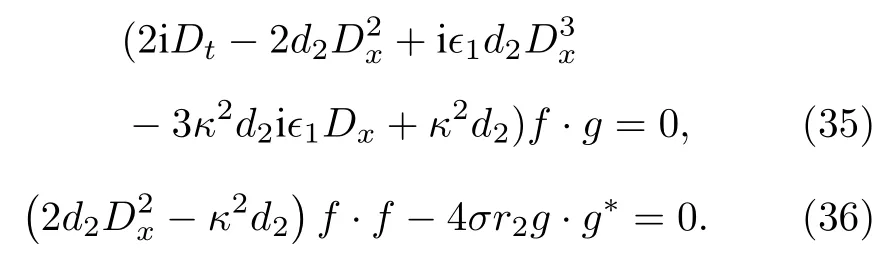
在傳統的非線性薛定諤模型(?1=0 )和Hirota系統 (?10 )的雙線性形式中, (35)式 和 (36) 式中常數κ被固定為零.當κ取零時雙線性方程組(35)式和 (36)式的多孤子解由傳統的Hirota形式描述.當κ0 且σd2/r2<0 (對應于散焦系統) 時,雙線性系統 (35)式和(36)式的多孤子解可以表示為[26]

其中關于 {ν}≡{ν1,···,νN} 的求和是關于所有可能的非對偶分布νi= ±1,i=1,···,N求和.如果 {ν′}= ?{ν} , 則 分 布 {ν′} 和 {ν} 被 稱作 是 對 偶的.由于 cosh 函數是偶函數, 所以對偶的分布給出相同的表達式, 所以求和只需要對非對偶分布求.在 (37)式和 (38)式中的K{ν}為

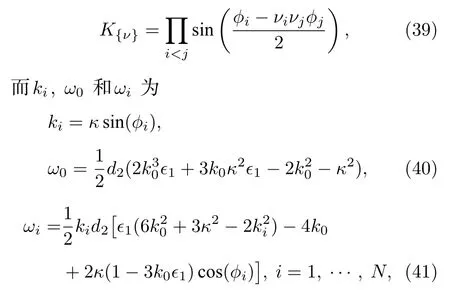
k0,ξi0,?i和?0為任意常數.

為了尋求孤子分子解, 我們先顯式寫下雙孤子解,

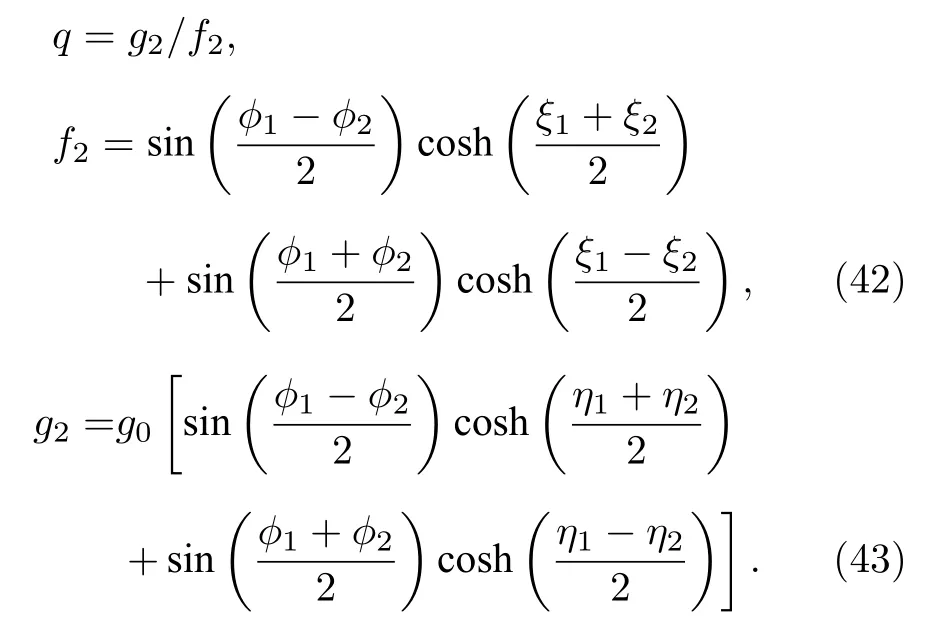
在一般情況下雙孤子解(42)式和(43)式是具有彈性相互作用的雙孤子態.圖10展示了這樣一個典型的雙孤子作用圖像, 其中采用的參數為(本節中統一采用的模型參數是d2=r2= ?σ=10?1=1 )

只有當二孤子的波速達到一種特殊共振狀態,使得孤子的吸引和排斥作用正好達到平衡時, 才能形成束縛態——孤子分子.

從表達式(41)式可知兩孤子形成孤子分子的速度共振條件為

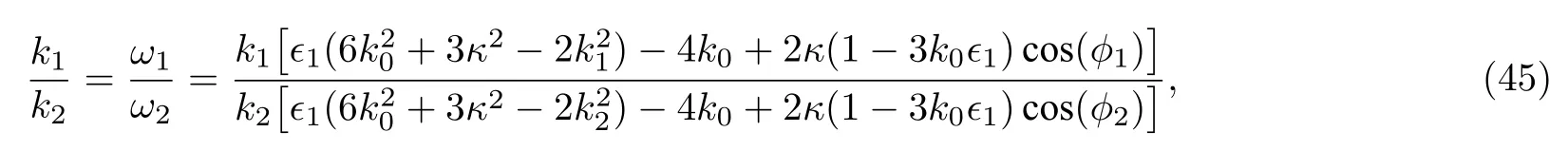
即

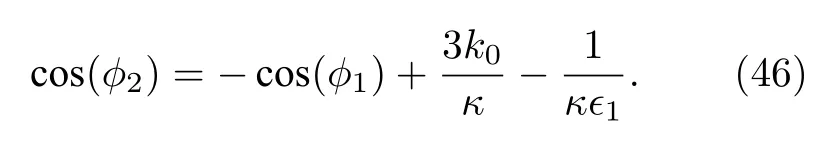
圖11展示了孤子分子對應的光強的密度圖(圖11(a))和立體圖(圖11(b)), 與圖對應的參數為

由于可積系統的多孤子之間的相互作用是彈性的, 孤子分子的存在只對應于一些特殊的多孤子, 自然孤子分子和通常的孤子的相互作用及孤子分子之間的相互作用也是彈性的.

(33)式的多暗孤子分子和多暗孤子的混合解由 (34)式, (37)式和 (38)式統一表達, 其中若有n對孤子的速度達到共振條件

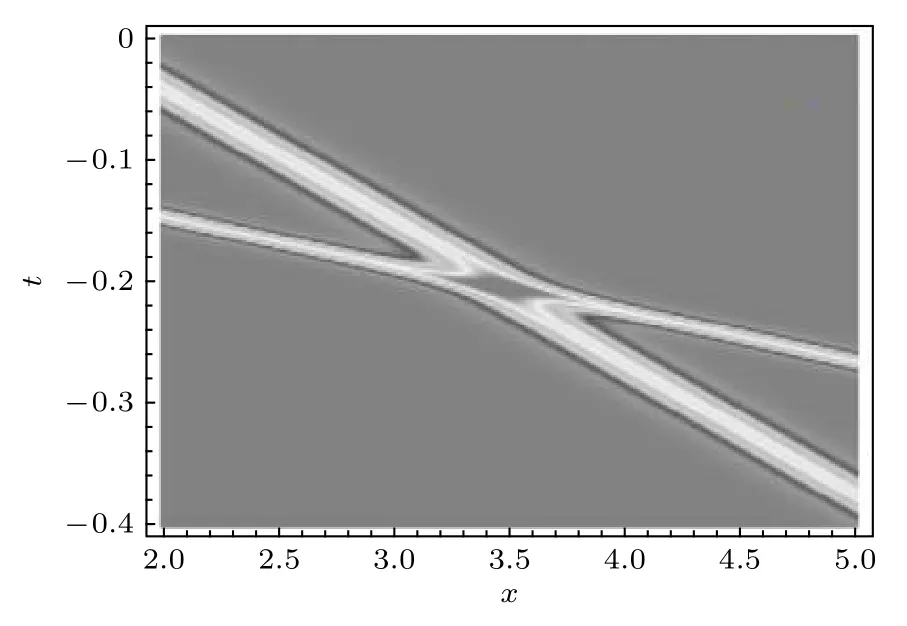
圖10 由 (42)?(43)式描述的二暗孤子相互作用的密度圖, 圖中參數由 (44)式給定Fig.10.Density plot of the interaction between two dark solitons described by Eq.(42)and Eq.(43) with the parameter selected from Eq.(44).

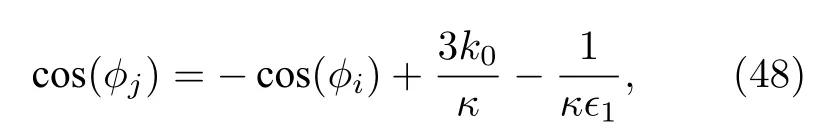
則解(34)式, (37)式和(38)式表示了n暗孤子分子和N?2n暗孤子的混合相互作用解.

圖12展示的是一個暗孤子分子和一個暗孤子的相互作用.圖中對應的參數為

圖11 (a) 由 (42) 式和 (43)式描述的暗孤子分子密度圖,圖中參數由 (47)式給定; (b) 與圖(a)對應的三維立體圖Fig.11.(a) Density plot of the dark soliton molecule described by Eq.(42) and Eq.(43) with the parameter selected from Eq.(47); (b) three dimensional plot related to Fig.(a).

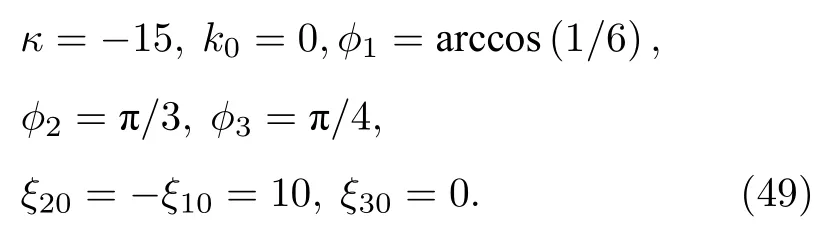
圖13展示了二暗孤子分子的相互作用.圖中對應的參數為

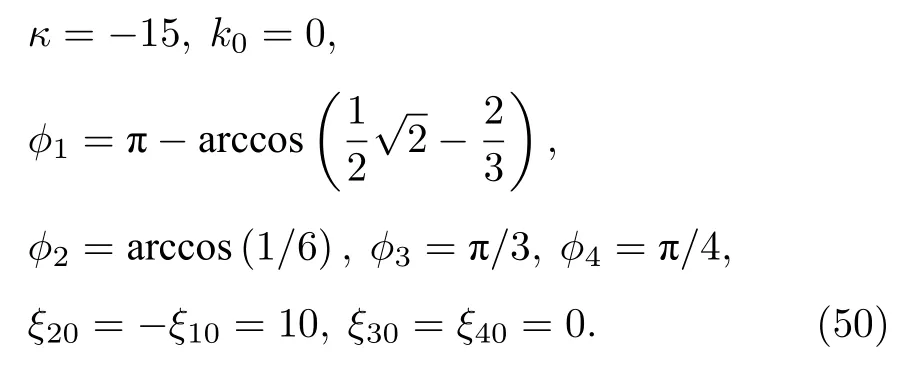
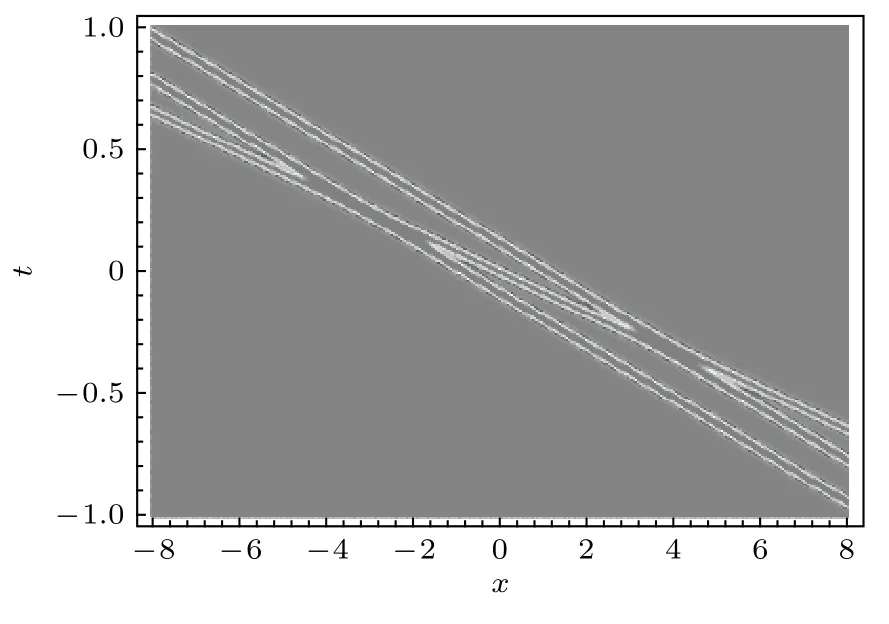
圖12 由 (34)式，(37)式和 (38)式描述的暗孤子分子和暗孤子的彈性相互作用的密度圖, 圖中參數由 (49)式給定Fig.12.Density plot of the interaction between a dark soliton molecule and a dark soliton described by Eq.(34),Eq.(37) and Eq.(38) with the parameter selected from Eq.(49).

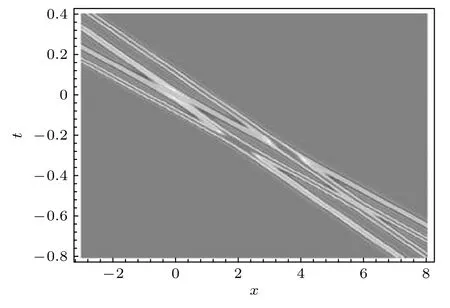
圖13 由 (34)式，(37)式和 (38)式描述的二暗孤子分子的彈性相互作用的密度圖, 圖中參數由 (50)式給定Fig.13.Density plot of the interaction between two dark soliton molecules described by Eq.(34), Eq.(37) and Eq.(38) with the parameter selected from Eq.(50).

4 結論和討論

本文首先系統研究了一個非線性光學中包含三階色散、自陡峭效應和自激Raman散射等高階非線性色散效應的一般非線性薛定諤方程的包絡行波解.結果發現高階非線性薛定諤系統具有非常豐富的周期波模式, 包括了多種亮孤子晶格(暗背景和灰背景的亮孤子晶格)和暗孤子晶格(雙谷暗孤子晶格和單谷暗孤子晶格).孤子晶格的多樣性導致了孤立子(孤子晶格周期解趨于無窮時的解)的多樣性: (暗背景)亮孤子, 具有灰背景的亮孤子, 暗孤子, 灰孤子, 超平暗孤子 (谷底一、二、三階變化率為零, 因此也可稱之為扭結-反扭結分子), 雙暗孤子分子等等.

對于一個可積的非線性光學系統——散焦型Hirota模型, 得到了一個新的雙線性形式, 利用這一新的雙線性形式, 給出了一個多孤子解的用雙曲余弦描述的緊致形式.從這一多孤子解出發, 引入速度共振條件即可得到多暗孤子分子和多暗孤子的混合解.暗孤子分子之間的相互作用以及暗孤子分子和暗孤子之間的相互作用是彈性相互作用.

孤子分子是當前非線性科學中的重要課題之一, 它象通常的孤子一樣也可以在物理學的各個領域中得到應用.在非線性系統中還存在各種各樣的局域激發模式, 如呼吸子、拱形(dromion) 解、團塊 (lump) 解 、尖 峰 子 (peakon)解 和 緊 子(compacton)解等等.因此自然可以期待得到各種各樣的其他類型的分子解, 如呼吸子分子、呼吸子-孤子分子、dromion分子、lump分子、dromionlump 分子、尖峰子分子、緊子分子等等.所有有關這些新類型的非線性局域激發的分子解及其可能的物理應用將在以后進行深入的研究.